Att_OMB Supporting Statement_3-29-07 Part B
Att_OMB Supporting Statement_3-29-07 Part B.doc
National Survey of Algebra Teachers
OMB: 1875-0243
SUPPORTING STATEMENT
Part B
National Survey of Teachers of Algebra
for the
NATIONAL MATHEMATICS ADVISORY PANEL
National Mathematics Advisory Panel
U.S. Department of Education
March 29, 2007
Table of Contents
Section B: Description of Statistical Methodology
B.1. Universe and Sampling Procedures 4
B.2. Statistical Methodology 6
B.3. Methods for Maximizing Response Rate 10
B.4. Tests of Procedures and Methods 11
B.5. Reviewing Statisticians……………………………………...........................................11
SECTION B: Collection of Information Employing Statistical Methods
B.1. Universe and Sampling Procedures
The contractor has designed a fully representative random sample of public school algebra teachers. The contractor has acquired a full universe of public schools (from the the USED Common Core of Data). In order to represent a cross-section of public school algebra teachers across the country, the survey sampling should stratify all of the schools nationwide based on type of locale, percentage of students who receive free or reduced-price lunch, and minority or foreign language density, and graded configuration of the school.
Schools sampled for the study and which agree to participate will be asked to provide comprehensive lists of the algebra I teachers, and all listed teachers will be included in the sample.
Each stratum of schools will operate as its own random sample and will be fielded independently. Respondents will be selected via a random selection process where each stratum is divided into representative mini-samples or replicates. Standard best practices of replicate control measures will be employed to ensure highest possible response rates.
Clarification of Statistical Methods (Per OMB’s Questions of March 27, 2007)
Question: The NSAT sample frame should include schools with missing data on any of the stratification variables. This could be done by defining a new stratum consisting of schools missing FRPL eligibility data, or redefining the current definitions of the strata to incorporate the missing schools (e.g., 40% or greater FRPL or missing FRPL). Because mailout preparations using the original sample are sufficiently far along at this point, NORC opted to select a supplemental sample of schools from the set of schools missing data on the stratification variables.
Because
the USED NCES Common Core of Data were
missing data across over 1200 stratification variables, we deleted
1,231 schools from the original frame due to missing strata
information. However, to represent these schools, we selected a
supplemental sample of 10 schools from the 1231 schools—the
supplemental frame. The new sample was selected such that a school of
size
![]() would
have the same selection probability if it were included in the
original frame. Under the previously implemented sample design, a
school of size
would
have the same selection probability if it were included in the
original frame. Under the previously implemented sample design, a
school of size ![]() has a selection probability of
has a selection probability of![]() ,
where
,
where
![]() is
the total number of teachers in the original frame. Suppose that the
supplemental frame contains a total number of
is
the total number of teachers in the original frame. Suppose that the
supplemental frame contains a total number of
![]() teachers.
Then, we should select
teachers.
Then, we should select
![]() teachers
from the supplemental frame using the same PPS sampling method. With
this sample size, a school of size
teachers
from the supplemental frame using the same PPS sampling method. With
this sample size, a school of size
![]() in the supplemental frame would have selection probability
in the supplemental frame would have selection probability![]() ,
which is the same probability if the school is included in the
original sample. Thus, this procedure ensures that a school with a
fixed size would have the same selection probability regardless of
which frame it is in.
,
which is the same probability if the school is included in the
original sample. Thus, this procedure ensures that a school with a
fixed size would have the same selection probability regardless of
which frame it is in.
The total estimated number of algebra 1 teachers over these 1,231 schools is 2169.99. Recall that the total estimated number of algebra 1 teachers over the 35,122 schools in the original frame is 65,865.88. This means that we should select (300*2169.99/65865.88)=9.88 schools from the supplemental frame. We selected 10 using the same PPS method used in the original draw. The frame is sorted by the other three stratification variables before selection.
The following tables show the distribution of the supplemental frame and the sample. Just over a third of the schools are in NY, but 7 of the 10 selected are in NY, reflecting their larger size as measured by the estimated number of algebra 1 teachers. Also, none of the 10 is in a rural area.
Supplemental Frame
Cumulative Cumulative
LSTATE04 Frequency Percent Frequency Percent
ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ
AK 78 6.34 78 6.34
AL 2 0.16 80 6.50
AZ 162 13.16 242 19.66
FL 2 0.16 244 19.82
GA 1 0.08 245 19.90
ID 12 0.97 257 20.88
IL 91 7.39 348 28.27
IN 16 1.30 364 29.57
KY 28 2.27 392 31.84
ME 16 1.30 408 33.14
MI 153 12.43 561 45.57
MN 1 0.08 562 45.65
MS 1 0.08 563 45.74
MT 43 3.49 606 49.23
NC 75 6.09 681 55.32
NE 3 0.24 684 55.56
NH 2 0.16 686 55.73
NJ 43 3.49 729 59.22
NY 441 35.82 1170 95.04
OH 3 0.24 1173 95.29
OK 4 0.32 1177 95.61
OR 1 0.08 1178 95.69
PA 1 0.08 1179 95.78
SD 1 0.08 1180 95.86
TX 3 0.24 1183 96.10
VA 32 2.60 1215 98.70
WA 1 0.08 1216 98.78
WI 14 1.14 1230 99.92
WY 1 0.08 1231 100.00
School is 40% or higher minority enrollment
Cumulative Cumulative
DMINOR Frequency Percent Frequency Percent
ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ
0 620 50.37 620 50.37
1 611 49.63 1231 100.00
School is high school/ middle school/ combined
Cumulative Cumulative
GRDRANGE Frequency Percent Frequency Percent
ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ
1 386 31.36 386 31.36
2 475 38.59 861 69.94
3 370 30.06 1231 100.00
School is urban/ suburban/ rural
Cumulative Cumulative
URBANICITY Frequency Percent Frequency Percent
ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ
1 644 52.32 644 52.32
2 268 21.77 912 74.09
3 319 25.91 1231 100.00
Supplemental Sample
Cumulative Cumulative
LSTATE04 Frequency Percent Frequency Percent
ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ
IL 1 10.00 1 10.00
MI 1 10.00 2 20.00
NY 7 70.00 9 90.00
VA 1 10.00 10 100.00
School is 40% or higher minority enrollment
Cumulative Cumulative
DMINOR Frequency Percent Frequency Percent
ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ
0 4 40.00 4 40.00
1 6 60.00 10 100.00
School is high school/ middle school/ combined
Cumulative Cumulative
GRDRANGE Frequency Percent Frequency Percent
ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ
1 7 70.00 7 70.00
2 2 20.00 9 90.00
3 1 10.00 10 100.00
School is urban/ suburban/ rural
Cumulative Cumulative
URBANICITY Frequency Percent Frequency Percent
ƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒƒ
1 8 80.00 8 80.00
2 2 20.00 10 100.00
B.2. Statistical Methodology
Clarification of Statistical Methods (Per OMB’s Questions of March 27, 2007)
The narrative follows up on the questions and requests from the March 27, 2007 phone conference between OMB, USED, and NORC on the National Survey of Algebra Teachers (NSAT). Brian requested three additions to the protocol; our responses to each are included below.
Question: Please provide minimum levels of precision for direct estimates from the survey taking into account the design effect. For example, for percentage estimates from single items an estimate of 50% would have a 95% confidence interval of plus or minus 3 percentage points. For a composite scale (drawn from in previous research), the expected mean based on prior research will be XX with a 95% confidence interval of x to X.
We have estimated a design effect of 2.5 for the overall sample. The design effect is substantial for some groups, but it’s about 2 or lower for most subgroups defined by the stratification variables. With minimum weight trimming, the overall design effect drops to 2, and the subgroup design effects are reduced to between 1.4 and 2. Note that these estimates are based on unequal weighting alone, i.e., they do not reflect potential clustering effect. The clustering effect should be small, however, given that we do not plan to sample more than 5 teachers from any school and the average cluster size is likely to be around 3. Depending on the magnitude of the intracluster correlation, clustering may increase the design effect by up to 10%, although it’s hard to estimate its impact with confidence. For the following precision and power calculations, we have assumed a design effect of 2.0 at the subgroup level.
To estimate the minimum levels of precision using a design effect of 2.0, the following tables show the 95% confidence intervals for (a) a composite scale with mean of 3.0 and standard deviation of 1.5, and (b) proportion estimates of 0.25, 0.50, and 0.75 estimated with effective sample sizes ranging from 50 to 400.
Estimates of 95% Confidence Intervals for a Composite Scale
Actual sample size |
Effective sample size (assuming design effect=2.0) |
Standard Error of the Mean |
95% CI for Estimated Composite Scale with mean=3.0 and SD=1.5 |
|
100 |
50 |
0.21 |
2.58 |
3.42 |
200 |
100 |
0.15 |
2.70 |
3.30 |
300 |
150 |
0.12 |
2.76 |
3.24 |
400 |
200 |
0.11 |
2.79 |
3.21 |
500 |
250 |
0.10 |
2.81 |
3.19 |
600 |
300 |
0.09 |
2.83 |
3.17 |
700 |
350 |
0.08 |
2.84 |
3.16 |
800 |
400 |
0.08 |
2.85 |
3.15 |
Estimates of 95% Confidence Intervals for a Proportion
Actual sample size |
Effective sample size (assuming design effect=2.0) |
95% CI for Estimated Proportion |
|||||
0.25 |
0.50 |
0.75 |
|||||
100 |
50 |
0.13 |
0.37 |
0.36 |
0.64 |
0.63 |
0.87 |
200 |
100 |
0.17 |
0.33 |
0.40 |
0.60 |
0.67 |
0.83 |
300 |
150 |
0.18 |
0.32 |
0.42 |
0.58 |
0.68 |
0.82 |
400 |
200 |
0.19 |
0.31 |
0.43 |
0.57 |
0.69 |
0.81 |
500 |
250 |
0.20 |
0.30 |
0.44 |
0.56 |
0.70 |
0.80 |
600 |
300 |
0.20 |
0.30 |
0.44 |
0.56 |
0.70 |
0.80 |
700 |
350 |
0.20 |
0.30 |
0.45 |
0.55 |
0.70 |
0.80 |
800 |
400 |
0.21 |
0.29 |
0.45 |
0.55 |
0.71 |
0.79 |
Question: Please provide additional power analyses. It would be helpful to see a table with a few different sample sizes for the subgroups (50, 100, 150, 200, 300) and the effect sizes that you will be able to detect in the comparisons with an alpha of .05 and power of 80% (taking into account the design effect). However, instead of the table, you could just report the minimum sample size that you will require for subgroup analyses and the associated effect size if you will set a hard rule on this. So, in this case, if you will not be conducting any subgroup comparisons with less than 200 teachers per cell, then you don’t need to do anything further since that is the power analysis you have already done [but please check the power analysis to ensure it was done correctly].
The following table was developed by Michael Yang for general guidance, and is applicable to the NSAT with the caveat that the NSAT sample size will be 800 or lower. The sample sizes here should be interpreted as “effective sample sizes”, that is, as the actual sample size divided by the design effect (provisionally assumed to be 2.0 for the NSAT).
Sample Size for Detecting a Pre-specified Difference Between Two Proportions (=.05, 1-=.80)
|
Effect Size |
|
|
Sample Size |
Effect Size |
|
|
Sample Size |
Effect Size |
|
|
Sample Size |
Two- Tailed Test |
.05 |
.95 |
.90 |
430 |
.10 |
.95 |
.85 |
140 |
.15
|
.95 |
.80 |
80 |
.90 |
.85 |
680 |
.90 |
.80 |
200 |
.90 |
.75 |
100 |
||||
.85 |
.80 |
900 |
.85 |
.75 |
250 |
.85 |
.70 |
120 |
||||
.80 |
.75 |
1,080 |
.80 |
.70 |
290 |
.80 |
.65 |
140 |
||||
.75 |
.70 |
1,240 |
.75 |
.65 |
330 |
.75 |
.60 |
150 |
||||
.70 |
.65 |
1,360 |
.70 |
.60 |
360 |
.70 |
.55 |
165 |
||||
.65 |
.60 |
1,460 |
.65 |
.55 |
380 |
.65 |
.50 |
170 |
||||
.60 |
.55 |
1,520 |
.60 |
.50 |
390 |
.60 |
.45 |
175 |
||||
.55 |
.50 |
1,550 |
.55 |
.45 |
390 |
.55 |
.40 |
175 |
||||
.50 |
.45 |
1,550 |
.50 |
.40 |
390 |
.50 |
.35 |
170 |
||||
.45 |
.40 |
1,520 |
.45 |
.35 |
380 |
.45 |
.30 |
165 |
||||
.40 |
.35 |
1,460 |
.40 |
.30 |
360 |
.40 |
.25 |
150 |
||||
.35 |
.30 |
1,360 |
.35 |
.25 |
330 |
.35 |
.20 |
140 |
||||
.30 |
.25 |
1,240 |
.30 |
.20 |
290 |
.30 |
.15 |
120 |
||||
.25 |
.20 |
1,080 |
.25 |
.15 |
250 |
.25 |
.10 |
100 |
||||
.20 |
.15 |
900 |
.20 |
.10 |
200 |
.20 |
.05 |
80 |
||||
.15 |
.10 |
680 |
.15 |
.05 |
140 |
|
|
|
||||
.10 |
.05 |
430 |
|
|
|
|
|
|
||||
One-Tailed Test |
.05 |
.95 |
.90 |
340 |
.10 |
.95 |
.85 |
110 |
.15
|
.95 |
.80 |
60 |
.90 |
.85 |
540 |
.90 |
.80 |
160 |
.90 |
.75 |
80 |
||||
.85 |
.80 |
710 |
.85 |
.75 |
195 |
.85 |
.70 |
95 |
||||
.80 |
.75 |
850 |
.80 |
.70 |
230 |
.80 |
.65 |
110 |
||||
.75 |
.70 |
980 |
.75 |
.65 |
260 |
.75 |
.60 |
120 |
||||
.70 |
.65 |
1,070 |
.70 |
.60 |
280 |
.70 |
.55 |
130 |
||||
.65 |
.60 |
1,170 |
.65 |
.55 |
295 |
.65 |
.50 |
135 |
||||
.60 |
.55 |
1,200 |
.60 |
.50 |
305 |
.60 |
.45 |
140 |
||||
.55 |
.50 |
1,220 |
.55 |
.45 |
310 |
.55 |
.40 |
140 |
||||
.50 |
.45 |
1,220 |
.50 |
.40 |
305 |
.50 |
.35 |
135 |
||||
.45 |
.40 |
1,200 |
.45 |
.35 |
295 |
.45 |
.30 |
130 |
||||
.40 |
.35 |
1,170 |
.40 |
.30 |
280 |
.40 |
.25 |
120 |
||||
.35 |
.30 |
1,070 |
.35 |
.25 |
260 |
.35 |
.20 |
110 |
||||
.30 |
.25 |
980 |
.30 |
.20 |
230 |
.30 |
.15 |
95 |
||||
.25 |
.20 |
850 |
.25 |
.15 |
195 |
.25 |
.10 |
80 |
||||
.20 |
.15 |
710 |
.20 |
.10 |
160 |
.20 |
.05 |
60 |
||||
.15 |
.10 |
540 |
.15 |
.05 |
110 |
|
|
|
||||
.10 |
.05 |
340 |
|
|
|
|
|
|
As the table shows, an effective minimum sample size of about 80, which is equivalent to an actual sample size of 160 under our design, will be needed to detect differences in proportions of .15 at the high and low extremes of proportion estimates (i.e,, .95-.80 and .20-.05) under a two-tailed test with alpha=.05 and power=.80. In the middle range of proportion estimates (e.g., .60-.45) the effective minimum sample size needed increases to 140, implying actual sample sizes of about 280 cases. The actual subgroup sample sizes range from 50 to roughly 500 in our sample. So, we are likely to be able to detect differences of 15% in most cases. For estimates that are below 40% or above 60%, we are likely to be able to detect differences of 10% among the largest subgroups. While we have not extended this exercise to composite scales, it appears that the NSAT will generally be suited to detect moderate to large effect sizes.
The analysis of the data collected from the survey will consist primarily of cross-classifications of frequency distributions and means for various reporting groups. The first step in the analysis is to assess the measurement properties of the items and scales used to measure the key constructs. Factor analysis is generally a useful tool for identifying and confirming common factors underlying the array of items, and we plan to use factor analytic methods to select items for the scales. NORC plans to use standard item-scale reliability assessments of the marginal contributions of each constituent item to the scale, and for estimating the reliability of the scale as a whole as defined by the optimal set of items.
The
tabulations will all be constructed using weighted counts of cases.
All
sampled teachers will have a base weight that reflects the selection
probability under the sample design. The base weight will be adjusted
for non-response through weighting class adjustments where the
sampling strata or collapsed strata serve as the weighting classes.
The final analysis weight for a teacher
![]() who
completes the survey can be expressed as
who
completes the survey can be expressed as
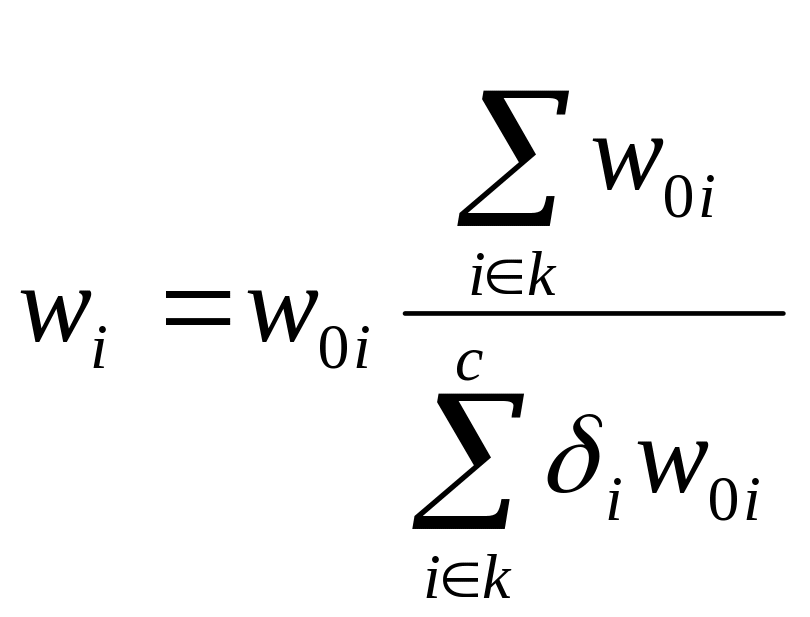
where![]() is
the base weight,
is
the base weight,
![]() is
a 0-1 response indicator, and
is
a 0-1 response indicator, and
![]() denote
the weighting class.
denote
the weighting class.
The non-experimental and cross-sectional design of the NSTA dictates that it will provide descriptive information rather than attempt to make causal inferences. Nonetheless, statistical significance of group differences will be of interest throughout the report. The complex sample design and clustering of teachers within sampled schools means that statistical tests must be based on variance estimates which do not assume simple random sampling. The contractor will employ appropriate estimation techniques, such as those available in SUDAAN, Wesvar, STATA, and HLM, in order to estimate statistical significance of group differences.
B.3. Methods to Maximize Response Rates
Two types of response rates are germane to the NSTA: the rate at which sampled schools agree to participate by providing the names of their algebra 1 teachers (“school response rate”), and the rate at which the teachers sampled within the participating schools (“the teacher response rate”).
Maximizing the school response rate. In the experience of NORC (the data collection contractor for the NSTA), district superintendents should always be notified of studies involving their schools in advance of contacting the school principals. Furthermore, larger districts will often require survey projects to submit a formal application prior to any contact with schools within those districts. Using a template developed by NORC in other school studies, NORC will prepare a “district research clearance package” to supply to any district which requires the study information in writing. This package will include information on the study’s purpose and funding, respondent burden, and number of respondents involved. Taking into account the short period of performance and the limited burden the study will have on schools, our overall approach to district gaining cooperation will include a notification letter to all districts with phone follow up in all larger school districts (defined provisionally as those with more than 10 schools with grades 8 or higher). This letter will briefly explain the study purpose and scope and will be sent via Fed Ex to either the superintendent or the district office responsible for reviewing research requests as soon as the districts are identified for inclusion in the study. The follow up phone calls to the larger districts will seek to determine whether a formal application is required and, if so, how to proceed with it as expeditiously as possible.
A week following the district letter mailing, except in those districts which will require additional treatment, NORC will send via Priority mail a letter to the principals of the sampled schools. The letter will include information on the study, including teacher burden, and assure the principals that we sent a letter to their district superintendent as well. In addition, the letter will notify the principals that someone from NORC will be calling within a week to answer questions and collect the names of their algebra 1 teachers.
Maximizing teacher response rate. The teacher response rate to the survey is calculated as the proportion of sampled teachers who return a completed questionnaire. NORC anticipates a 80% response rate to the teachers survey. However, to maximize this rate, NORC will implement a multimodal (mail, phone, e-mail) contact strategy that includes multiple attempts to reach each individual teacher sampled. This approach is built on the principles developed by Don A. Dillman in his Mail and Internet Surveys (2nd edition) (John Wiley & Sons, 2000) and is designed to increase response rates by giving sampled teachers many opportunities to participate in the survey. Five to seven attempts to contact the respondent will be undertaken. The contractor (NORC) is also providing incentive payments of $20 per sampled teacher (included along with the first questionnaire mailing).
The first contact will be through the mail in early April, and will consist of a “prenotice” letter briefly explaining that the teacher has been selected to participate in the study and that the questionnaire will arrive in the next few days. The first questionnaire mailing will include the instrument, a cover letter explaining the purpose of the study, a check for $20 as a token of our appreciation, and a prepaid return envelope for the completed questionnaire. One week after the first mailing, NORC will send a postcard to each teacher, thanking them if they have already completed or reminding them to do so if not. The postcard will also provide them with a phone number and e-mail to contact in case they need another survey mailed out to them. Three weeks after the first mailing, NORC will send a replacement questionnaire and a follow-up letter requesting that they complete and mail back the survey. Four weeks after the first mailing, NORC will begin phone prompts to remaining non-respondents, and use e-mail if available and efforts to contact by phone were unsuccessful. Six weeks after the initial mailing, NORC will mail out a third and final copy of the questionnaire to those who have not yet responded along with a cover letter and postage-paid return envelope.
B.4. Tests of Procedures and Methods
The NSTA has undergone an accelerated period of testing of the items in the questionnaire, and of obtaining expert advice on the revised items. The proposed questionnaire was tested as follows:
NORC project staff conducted cognitive interviews with fewer than 9 algebra I teachers in Chicago;
NORC project staff convened a panel of questionnaire design experts from the NORC staff to review the draft questionnaire item by item and provide feedback on how to improve the instrument.
NORC obtained feedback from 4 experts on the National Mathematics Advisory Panel.
B.4. Reviewing Statisticians
The statistical experts associated with this survey are Dr. Michael Yang, Senior Statistician on the project at NORC (202-223-9160). At USED, Grover J. (Russ) Whitehurst, Director of the Institute for Educational Sciences will provide statistical oversight. (Point of Contact in the Department of Education for this survey is Marian Banfield, National Math Panel, Office Planning, Evaluation and Policy Development (202-401-7767).
| File Type | application/msword |
| File Title | SF-83-1 SUPPORTING STATEMENT |
| Author | marian.banfield |
| Last Modified By | kate.mullan |
| File Modified | 2007-03-30 |
| File Created | 2007-03-30 |
© 2025 OMB.report | Privacy Policy