Att_OMB Part B Final
Att_OMB Part B Final.doc
Impact Evaluation of Mandatory-Random Student Drug Testing
OMB: 1850-0818
Impact Evaluation of Mandatory-Random Student Drug Testing
Supporting Statement for Request for OMB Approval of Data Collection Part B
Contract No: ED-04-CO-0041/0006
Prepared for
U.S. Department of Education
IES/NCEE
555 New Jersey Avenue, NW, Room 502C
Washington DC 20208
Prepared by
RMC Research Corporation
111 SW Columbia Street, Suite 1200
Portland, OR 97201
Mathematica Policy Research, Inc.
P.O. Box 2393
Princeton, NJ 08543-2393
COSMOS Corporation
3 Bethesda Metro Center, Suite 950
Bethesda, MD 20814
March 30, 2007
Impact
Evaluation of Mandatory-Random
Student Drug Testing
Supporting
Statement for Request for
OMB Approval of Data Collection
Prepared for
Paul Strasberg
U.S. Department of Education
IES/NCEE
555 New Jersey Avenue, NW, Room 502C
Washington DC 20208
Prepared by
Eric L. Einspruch
Kelly J. Vander Ley
RMC Research Corporation
Susanne James-Burdumy
John Deke
Kevin Booker
Mathematica Policy Research, Inc.
Jennifer Scherer
COSMOS Corporation
March 30, 2007
Contents
B. Collection of Information Employing Statistical Methods 1
1. Respondent Universe and Sampling Procedures 1
2. Statistical Methods for Sample Selection and Degree of Accuracy Needed 2
3. Methods
to Maximize Response Rates and Deal With Issues of
Nonresponse 8
4. Test of Procedures and Methods to be Undertaken 9
5. Individuals Consulted on Statistical Aspects of the Design 9
Appendices are attached as
separate documents.
Appendix A Active Consent
Appendix
B Student Survey
Appendix C Schoolwide Records Collections
Form
Appendix D School-Level Drug Testing Collection Form
Appendix E Staff Interview Topical Question Guide
Exhibits
Exhibit 5 Minimum Detectable Effect on Drug Use by Subgroup 5
Exhibit 6 Minimum Detectable Effect on Drug Use for the Contamination Analysis 8
B. Collection of Information Employing
Statistical Methods
1. Respondent Universe and Sampling Procedures
Below, we describe the respondent universe and sampling procedures for the impact study. We then describe these aspects of the study for the study of contamination.
Sample for the Impact Study
The impact study will include all grantees and schools that are recipients of OSDFS grants for Mandatory Random Student Drug Testing in Fiscal Year 2006. There will be no sampling of grantees or of schools within grantees. Therefore, the study will be representative of the types of grantees that apply for OSDFS grants. The study sample is not designed to represent schools that would use MRDT without an OSDFS grant. Although schools are not sampled, students within schools will be selected using stratified random sampling.
Based on initial enrollment and activity participation rates provided by grantees in their applications, we estimate that each high school included in the study will have an average of 1,190 students, of whom 33%, or 390 students, who will be subject to MRDT upon their school’s initiation of their district’s MRDT policy. The remaining 800 students in the average study school will not be subject to drug testing, although their behavior may be affected when the school adopts MRDT for the 390 students who participate in competitive school activities. Consequently, across the 45 schools included in the study, the total respondent universe will consist of approximately 53,500 students, of whom approximately 26,750 will be in treatment schools, and of whom approximately 8,800 will be subject to MRDT requirements.
The study team will use stratified (by grade) random sampling to identify the students in each school that we will approach about participating in the study (see section 2a below for details of the student sampling).
Sample of External Schools (Contamination Study)
For the contamination study, we will purposefully select external schools that are similar to schools in the impact study. Similarity will be determined by data available in the CCD and test score data available from www.schoolmatters.com. We will sort all external high schools in a state by their similarity to schools in the impact study. We will begin recruiting the most closely matched schools based on these variables and attempt to recruit those schools. We will continue in our recruitment effort until we have identified a school that agrees to participate for each grantee by continuing with the list until we have met our recruitment target.. Students within the external sample of schools will be sampled for participation in the study as described above.
2. Statistical Methods for Sample Selection and Degree of Accuracy Needed
As noted above, there are 2 components of the study (1) the impact study based on 45 schools that are part of the OSDFS grants and (2) the contamination study based on 12 external schools and 12 control schools from the impact study. The sample selection process and degree of accuracy needed for each of these components are discussed, in turn, below.
Impact Study
Sample Frame
The sample frame for the impact study includes all Grade 9 through 11 students in the study schools in February 2007. In fall 2007 and spring 2008, the sample frame will include all Grade 9 through 12 students in the study schools.
Stratification
We will stratify by grade, drawing a number of students from each grade that is proportional to the size of that grade in the school. At baseline, we will sample students in Grades 9, 10, and 11. At follow-up, we will sample all students who had participated in the baseline survey who remained in the school (or who transferred to a school within the same district) and draw a new sample of Grade 9 students. We will also refresh the sample of students in Grades 10, 11, and 12 by replacing students who left the study schools with a sample of students who are new to the study schools.
Sample Sizes
Approximately 200 students at each school will complete student surveys. Assuming 20 treatment schools and 16 control schools participating in the study,1 8,400 students will respond to each of the study’s surveys. To attain this sample size, we will initially sample 312 students at each school. We expect a consent rate of 80% and a survey response rate of 80%,2 which will lead to 200 of those 312 actually completing a survey. The first round of sampling will take place immediately upon approval by OMB of this package so that the baseline student survey can be administered to sampled students during spring 2007.
We estimate that approximately 30% of students who respond to the baseline survey will leave each study school by dropping out or moving. Thus, of the 7,200 respondents to the baseline survey, we expect 5,040 to also respond to the follow-up surveys. At follow up we will refresh the sample with 2,160 new students to replace those that left.
Degree of Accuracy Needed
In order to assess appropriate sample sizes for the evaluation, we adopt a precision standard using impact results found in other evaluations. Goldberg et al. (2003) found an impact of 10.2 percentage points on illegal drug use between the baseline and follow-up surveys. Consequently, the minimum detectable impact (MDI) for the evaluation should ideally be no larger than 10.2 percentage points, so the evaluation has an 80% chance of detecting an impact of this magnitude that is statistically significant at the 0.05 level. Goldberg also found a control group mean of 41.7% for athletes’ illegal drug use during the past 30 days, while Johnston et al (2005) estimated a corresponding mean of 18.3% for all students in Grade 10, so we assumed control group means of 10%, 20%, and 30% for the purposes of the power calculations. Thus, the desired minimum detectable effect size of the study is 0.22 of a standard deviation or less3. Our goal is to detect this effect size for subgroups of students defined by their participation in covered activities.
Minimum Detectable Effects
Exhibit 5 presents minimum detectable effects for subgroups of differing sizes. For the calculations in this table we assumed that 50% of between-school variation in drug use can be accounted for by regression adjustment. We also assumed that 50% of within-school variation in drug use can be accounted for by regression adjustment for students who completed the baseline survey. For students that did not complete the baseline survey (approximately one-third of our sample), regression adjustment provides no benefit. Thus we assume that overall regression adjustment explains just 25% of within-school variation in drug use. Additional assumptions are described in the footnote to Exhibit 5.
If one-third of students participate in activities, the study will be able to detect an effect size of at least 0.18 of a standard deviation among activity participants, which is less than the 0.22 standard deviation impact observed by Goldberg (row 2). Among a 25% subgroup of activity participants, the study will be able to detect an effect size of at least 0.25 of a standard deviation. Among activity participants in a 50% subgroup of schools, the study will be able to detect an effect size of at least 0.28 of a standard deviation.
Exhibit 5
Minimum
Detectable Effect on Drug Use by Subgroup
|
|
|
Minimum Detectable Impacts |
|||
Subgroup |
No. of Treatment/ Control Schools |
No. of Students Per School at Follow-Up (accounting for consent and response rates) |
In Effect Size (Standard Deviation) Units |
In Percentage Points For Outcomes With Prevalence Rates: |
||
30% |
20% |
10% |
||||
Full Sample |
20/16 |
200 |
0.17 |
7.6 |
6.5 |
4.6 |
Activity Participants |
20/16 |
67 |
0.18 |
8.1 |
6.8 |
4.8 |
25% of Activity Participants |
20/16 |
17 |
0.25 |
11.3 |
9.5 |
6.9 |
Activity Participants in a 50% Subgroup of Schools |
10/8 |
67 |
0.28 |
12.7 |
10.7 |
7.8 |
Note. The minimum detectable impacts were calculated assuming (a) a 2-tailed test, (b) 5% significance (α) level, (c) an 80% level of power , (d) a reduction in between-school variance of 50% and a reduction in within-school variance of 25% owing to the use of regression models to estimate impacts, and (e) an intraclass correlation of .05 based on results in the literature (Murray, Varnell, & Biltstein, 2004) . The figures were calculated using the following formula:
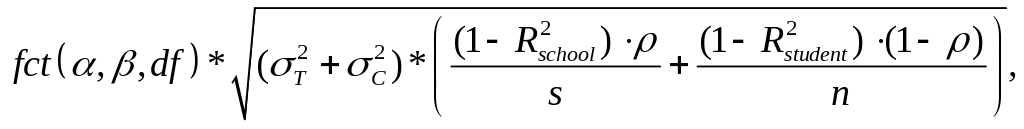
where
![]() (
(![]() )
is the variance of the outcome variable in the treatment (control)
group, R2
is the regression R-squared value (0.50 for schools, 0.25 for
students), r is the intraclass correlation at the school level
(.05), s is the number of treatment (control) schools and n is the
available follow-up survey sample size for the treatment (control)
group. The number of degrees of freedom is equal to the number of
schools minus the number of blocks minus one. We assume two schools
per block, so if there are 36 schools, then there are 17 degrees of
freedom.
)
is the variance of the outcome variable in the treatment (control)
group, R2
is the regression R-squared value (0.50 for schools, 0.25 for
students), r is the intraclass correlation at the school level
(.05), s is the number of treatment (control) schools and n is the
available follow-up survey sample size for the treatment (control)
group. The number of degrees of freedom is equal to the number of
schools minus the number of blocks minus one. We assume two schools
per block, so if there are 36 schools, then there are 17 degrees of
freedom.
Adjustment for Multiple Comparisons
When a large number of statistical tests are performed, the chances are good that at least one of them will appear statistically significant by chance, even if no true significant effects exist. This is known as the problem of “multiple comparisons.” We will address this issue using the heuristics suggested by the What Works Clearinghouse.4 Specifically, for multiple outcome measures within a domain, or when testing multiple subgroups, we will declare a statistically significant impact of drug testing within an outcome domain if any of the following hold:
At least half of the estimated impacts within a domain are statistically significant with the same sign, and no impacts are of the opposite sign (regardless of statistical significance),
The effects are found to be jointly significant through an omnibus test.
The mean effect size for all outcomes in the domain is significant.
At least one of the impacts is significant after applying a relevant multiple comparison procedure. Examples of such procedures include Benjamini & Hochberg (1995) and Westfall (1997).
The effect of multiple comparison adjustment on the statistical power of the study will depend on how domains are structured and how impacts are calculated. The minimum detectable effects presented in tables B2.1 and B2.2 are for a joint outcome measure within a domain, in which the joint measure is formed using all of the individual outcomes in that domain. The minimum detectable effect for a single outcome measure within a domain that includes multiple measures would be higher (that is, statistical power would be lower).
Unusual Problems Requiring Specialized Sampling Plans
We do not anticipate any unusual problems requiring specialized sampling procedures.
Use of Periodic Data Collection Cycles to Reduce Burden
The same survey instrument will be used to collect data on students at baseline (spring 2007) and both follow-ups (fall 2007 and spring 2008). It will also be used to collect performance reporting data in spring 2009 and spring 2010.
Study of Contamination
Sample Frame
The sample frame for the contamination study is the same as for the impact study. It includes all students in Grades 9 through 11 in the external schools in spring 2007. In fall 2007 and spring 2008, the sample frame will include all students in Grades 9 through 12 in the external schools.
Stratification
As described above, we will stratify by grade, drawing a number of students from each grade that is proportional to the size of that grade in the school.
Sample Sizes
We will randomly sample 312 students in each of the 12 external schools. We expect consent and survey response rates of 80% each. We estimate that 30% of students will leave the schools between the baseline and follow-up years. Under these assumptions, we will have 2,400 students in the contamination analysis, of which 1,680 will have completed a baseline survey.
Degree of Accuracy Needed
For the contamination analysis, the study will be able to detect a minimum detectable effect of 0.21 of a standard deviation (Exhibit 6). This assumes 12 external schools compared to 12 control schools, with 200 students with completed surveys at each school (accounting for consent and survey response rates). Other assumptions are the same as above.
Exhibit 6
Minimum
Detectable Effect on Drug Use for the Contamination Analysis
|
|
Minimum Detectable Impacts |
|
Design Assumptions |
No. of Students Per School at Follow-Up (accounting for consent and response rates) |
In Effect Size (Standard Deviation) Units |
Percentage Points (assuming 30% of students use drugs) |
12 grantee schools, 12 control schools |
200 |
0.21 |
9.2 |
|
|
|
|
Note. The minimum detectable impacts in effect size units were calculated assuming (a) a 2-tailed test, (b) 5% significance (α) level, (c) an 80% level of power , (d) a reduction in between-school variance of 50% and a reduction in within-school variance of 25% owing to the use of regression models to estimate impacts, and (e) an intraclass correlation of .05 based on results in the literature (Murray, Varnell, & Biltstein, 2004). The figures were calculated using the following formula:
![]()
where R2 is the regression R-squared value (0.50 for schools, 0.25 for students), is the intraclass correlation at the school level (.05), s is the number of treatment (control) schools and n is the available follow-up survey sample size for the treatment (control) group. The number of degrees of freedom is equal to the number of schools minus the number of blocks minus one (that is, df = 24-12-2 = 10).
Unusual Problems Requiring Specialized Sampling Plans
We do not anticipate any unusual problems requiring specialized sampling procedures.
Use of Periodic Data Collection Cycles to Reduce Burden
The same survey instrument will be used to collect data on students at baseline (spring 2007) and both follow-ups (fall 2007 and spring 2008).
3. Methods to Maximize Response Rates and Deal With Issues of Nonresponse
Obtaining high response rates will be critical to the success of the study. It will be particularly important to obtain response rates that are not only high overall, but that are approximately equal in the treatment and control schools and external schools. This will be challenging due to the fact that treatment schools will be implementing MRDT, while control group and external group schools will not.
We will maximize the response rates to the survey by distributing survey instruments that are straightforward and easy for respondents to complete and by following up with nonresponders in each school using a variety of methods such as mail, fax, and telephone. We will rely heavily on the principals and the drug testing program coordinators at each school (including staff who were designated to coordinate the program at control schools) to assist us in contacting the sampled respondents at school and at home. Nonresponse bias will be examined and statistically controlled for if necessary.
4. Test of Procedures and Methods to be Undertaken
No tests of the procedures for data collection will be conducted. However, the student survey has been modeled largely on the form used for the SATURN study (Goldberg, et al., 2003) which, in itself, drew heavily from a large periodic national survey of substance use among high school students. Therefore, the survey forms contain instructions and questions that have already been pre-tested for their reliability and validity.
5. Individuals Consulted on Statistical Aspects of the Design
The statistical aspects of the design have been reviewed thoroughly by staff at the Institute of Education Sciences, contractor staff on the study, and TWG members. The following individuals have worked closely in developing the statistical procedures.
Name |
Title |
Telephone |
(IES Staff) |
|
|
Paul Strasberg |
Education Research Analyst |
(202) 219-3400 |
Marsha Silverberg |
Economist |
(202) 208-7178 |
(RMC Research Staff) |
|
|
Eric Einspruch |
Senior Research Associate |
(800) 788-1887 |
Kelly Vander Ley |
Senior Research Associate |
(800) 788-1887 |
(Mathematica Policy Research Staff) |
|
|
Susanne James-Burdumy |
Senior. Researcher |
(609) 275-2248 |
John Deke |
Senior Researcher |
(609) 275-2230 |
Kevin Booker |
Researcher |
(202) 484-4838 |
(COSMOS Staff) |
|
|
Jennifer Scherer |
Executive Vice President and Chief Operating Officer |
(301) 215-9100 |
Relevant Advisory Panel Members (Conceptualization Phase) |
||
Robinson Hollister |
Professor of Economics, Swarthmore College |
610-328-8105 |
Rebecca Maynard |
Professor of Education, University of Pennsylvania |
215-898-3558 |
References
Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society (Series B), 57, 289–300.
Goldberg, L., et al., (2003). Drug testing athletes to prevent substance abuse: Background and pilot study results of the SATURN (Student Athlete Testing Using Random Notification) study. Journal of Adolescent Health, 32, 16–25.
Johnston, L.D., O’Malley, P.M., Bachman, J.G., & Schulenberg, J.E. (2005). Monitoring the Future national results on adolescent drug use: Overview of key findings, 2004. (NIH Publication No. 05-5726). Bethesda, MD: National Institute of Drug Abuse.
Murray, D.M., Varnell, S.P., & Biltstein, J.L. (2004). Design and analysis of group-randomized trials: A review of recent methodological developments. American Journal of Public Health, 94, 423–432.
Westfall, P. (1997). Multiple Testing of General Contrasts Using Logical Constraints and Correlations. Journal of the American Statistical Association, 92, 299–306.
1Since the grant award, 7 schools left the study because their district school boards did not pass the drug testing policy. The power analysis allows for the possibility that 9 additional schools may leave the study, which would reduce the number of schools to 36.
2Goldberg et al. (2003) conducted a study of student drug testing and obtained response rates of between 77 and 87 percent.
3The
standard deviation of a binary variable with mean p is
![]() .
In this case, p = 0.30, so the standard deviation
is 0.46. This implies that the effect size of a 10.2 percentage
point impact is 0.102/0.46 = 0.22.
.
In this case, p = 0.30, so the standard deviation
is 0.46. This implies that the effect size of a 10.2 percentage
point impact is 0.102/0.46 = 0.22.
4www.whatworks.ed.gov/reviewprocess/rating_scheme.pdf
| File Type | application/msword |
| File Title | Impact Evaluation of Mandatory-Random Student Drug Testing |
| Author | Mollie O'Ryan Rawson |
| Last Modified By | Sheila.Carey |
| File Modified | 2007-04-26 |
| File Created | 2007-04-26 |
© 2026 OMB.report | Privacy Policy