ACF Response
ACF Response to OMB RI 36m 02 28 08 FINAL.doc
Enhanced Services for the Hard-to-Employ Demonstration and Evaluation: Rhode Island 36-Month Follow-Up Data Collection
ACF Response
OMB: 0970-0337
RESPONSE TO OMB QUESTIONS
What was the burden for each of the ICs in the 18 month study, and what was the incentive amount offered?
The burden hours approved by OMB for the 15/18-month data collection were 45 minutes for the core survey, plus 45 minutes for the child add-on modules to be completed with up to two focal children. The parent was paid $20 for completing the core survey and $30 if a focal child-add on module was completed (note that a maximum of $30 was paid for the child add-on module regardless of whether there was one focal child or two).
The approved respondent burden for the youth survey was 45 minutes. The child is paid a $20 gift card for completing the survey. Lastly, the approved respondent burden for the young child assessment is 45 minutes, but the young child assessments are typically taking about 30 minutes. If the child attempts the assessment, they are given an age-specific toy valued at $10.
On page 2 of the supporting statement, ACF states its intention to use instrumental variables estimation techniques. However, there doesn't seem to be any discussion of how this analysis will be conducted (e.g. what the instrumental variables will be, etc.). Can ACF elaborate?
In order to estimate the effects of changes in depression as a result of the mental health intervention on changes in outcomes for children, an instrumental variables (IV) estimation approach may be utilized. The IV estimation method addresses the biases commonly associated with correlational estimation strategies (see Gennetian, Morris, & Bos, 2005; Angrist, Imbens, & Rubin, 1996). The IV approach leverages the exogenous variation as a result of the assignment to the intervention and compares the relative rate of change in depressive symptoms to the rate of change in child outcomes.
Using Pi to denote assignment to treatment or control groups, Xi to denote a key independent variable of interest and Yi to denote a key outcome of interest (e.g., children’s behavior problem scores), the effect of Xi on outcome Yi is estimated by comparing the effect of Pi on Yi to the effect of Pi on Xi:
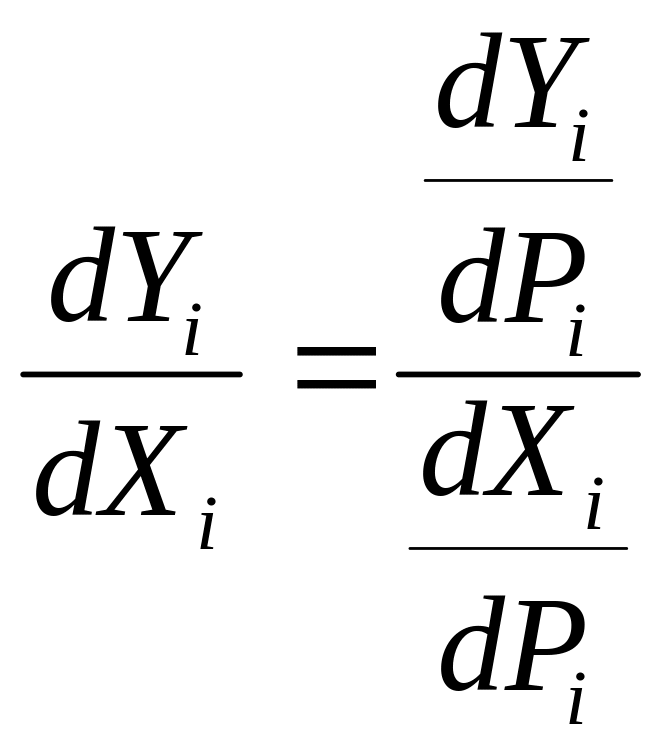 , (1)
, (1)
where
![]() is
the effect of Xi on Yi,
is
the effect of Xi on Yi,
![]() is
the effect of Pi on Yi,
and
is
the effect of Pi on Yi,
and
![]() the
effect of Pi on Xi.
In the case of a single X variable, the IV estimate of the effect of
X on Y is given by (1).
the
effect of Pi on Xi.
In the case of a single X variable, the IV estimate of the effect of
X on Y is given by (1).
Instrumental variables estimation of a model with a single Xi consists of a first stage equation in which Xi is predicted by Pi and other controls, and a second stage equation in which Yi is a function of the predicted value of Xi. More formally, this is expressed as follows:
![]() ,
as the first stage equation, and (2)
,
as the first stage equation, and (2)
![]() ,as the second stage equation (3)
,as the second stage equation (3)
A number of assumptions are necessary to ensure that the IV estimator
captures the change in outcome Yi associated with this
randomly induced change in Xi (Angrist, Imbens, &
Rubin, 1996). Data generated from random assignment designs
meet these assumptions, and provide a rare opportunity to tease out
the relative effects of depression from economic outcomes on
low-income children’s development. A primary assumption
of this technique is that the instrument Pi is
uncorrelated with the error term in the first stage equation.
Because not all possible variables Zi are known, one
cannot usually be certain that
![]() is
indeed true. In our work, Pi is a random variable since it
is based on the random assignment of the parent to either the
treatment or control groups. Random assignment of an individual
or family to a treatment group or to a control group is uncorrelated
with any observable or unobservable factors that may confound
estimated effects on children’s development. A second
assumption is that there must be a meaningful effect of the
instrument Pi on the independent variable of interest Xi,
(depressive symptomatology on the part of the parent). A final
assumption1
is that any effect of the program Pi on the outcome Yi
must be mediated by the independent variable Xi for Pi
to be a valid instrument for Xi (the “exclusion
restriction”). When there is an effect of Pi
on Yi that is not mediated by Xi, the
instrumental variable estimator may misattribute this effect to Xi,
causing the estimate of Xi
is
indeed true. In our work, Pi is a random variable since it
is based on the random assignment of the parent to either the
treatment or control groups. Random assignment of an individual
or family to a treatment group or to a control group is uncorrelated
with any observable or unobservable factors that may confound
estimated effects on children’s development. A second
assumption is that there must be a meaningful effect of the
instrument Pi on the independent variable of interest Xi,
(depressive symptomatology on the part of the parent). A final
assumption1
is that any effect of the program Pi on the outcome Yi
must be mediated by the independent variable Xi for Pi
to be a valid instrument for Xi (the “exclusion
restriction”). When there is an effect of Pi
on Yi that is not mediated by Xi, the
instrumental variable estimator may misattribute this effect to Xi,
causing the estimate of Xi
![]() to
be biased. Because this intervention is targeted at parents’
depression, any effect on children must be a result of changes in
parents’ depression and not other changes deriving directly
from the intervention.
to
be biased. Because this intervention is targeted at parents’
depression, any effect on children must be a result of changes in
parents’ depression and not other changes deriving directly
from the intervention.
On what basis does ACF estimate a response rate of 80%? What have been the response rates to date for earlier components of this study?
We are on target to achieve at least an 80 percent response rate on the parents for the core and add-on survey at 15/18 months, and of those parents who have agreed to participate, we are on target to achieve 90% of their children for the direct child assessments and youth surveys. Therefore, we expect similar response rates at this, 36-month, follow-up point. From our experience, achieving such high response rates requires the use of appropriate incentives for participation, along with in-person tracking of sample members to locate them for the survey effort. In other studies with follow-up periods that extended to 3 and 4 years of follow-up on similarly disadvantaged populations (e.g., the Connecticut Jobs First evaluation, Florida’s Family Transition Program), we were able to receive similarly high response rates using these strategies.
Does ACF plan to adjust for potential multiple comparison bias?
As discussed in more detail below, we do not plan to adjust for multiple comparisons explicitly, but we do intend to incorporate the rationale behind multiple comparison adjustments in our analytic plan.
Our goal is to incorporate the spirit of the idea by limiting the number of comparisons we make. First, we would focus the analysis initially on a small number of outcomes for which we have firm hypotheses about program impacts. Second, we would present results on a small number of subgroups. For example, in analyzing data for the six-month follow-up in Rhode Island, we plan to show results by depression severity at baseline, by race and ethnicity, by age of onset of depression, and by health status at baseline. Before we begin to analyze data at the 36-month follow-up point, we will write an evaluation plan specifying exactly what the core outcomes and subgroups would be. Conclusions about the effectiveness of the program at 36 months would be based on these relatively few comparisons. Once these conclusions are reached, we would conduct exploratory analyses, such as analyses of subgroups for which there is not a strong hypothesis and the full range of outcomes from the survey and administrative records.
There is no consensus in the statistics or evaluation fields about how to adjust for multiple comparisons. Many different methods have been proposed (e.g., Bonferroni corrections, Benjamini-Hochberg corrections (1995)2, the methods of Tukey, Fisher, Scheffé, Dunnett, Duncan, and others as reviewed by Darlington (1990)3, and resampling methods such as those described by Westfall. There is no consensus on whether corrections should be made across all outcomes or within certain domains or whether the purpose of multiple comparisons is to avoid bias in conclusions about whether the intervention had any effects at all or in conclusions about particular effects.
Most standard corrections for multiple comparisons are conservative by design. They make it harder to find false positives, but they do so by making it harder to find true positives. In other words, the cost of avoiding drawing the wrong positive conclusion is that we would reject drawing positive conclusions about effective programs. Finally, in our published reports we will include a technical note about the likelihood of getting statistically significant findings by chance to address potential questions regarding multiple comparison bias.
Can ACF elaborate on which sub-groups it will be focusing its subgroup analyses on?
Before turning to the specifics of our response, we want to highlight that in conducting subgroup analyses, we think it critical that subgroups are chosen carefully to test a small set of discrete hypotheses about how effects might differ across groups of parents or children. In that spirit, we plan to examine the following subgroups for the adult depression and economic outcomes: parents’ baseline depression severity; parents’ race and ethnicity, parents’ age of onset of depression, and health status at baseline. If these differentiate effects on adult depression, we would of course want to carry through these same subgroups to the analyses on the effects on parenting mediators and outcomes for children. In addition, we plan to examine differences in child outcomes by child age and by child gender, key child characteristics that have been identified in the literature on the effects of depression on children.
Supporting statement part A says that certain items may be deleted from the instruments if pre-testing reveals that the surveys take longer than an hour. It also says that questions about mental health and employment would be candidates for deletion. Since this intervention is designed to assess impacts on the mental health and employment prospects of low-income TANF beneficiaries who are hard-to-employ because they have depression, why has ACF decided to delete these from these categories of questions?
When considering items or sections that would be deleted if the pre-test results showed that the survey was taking longer than the allotted burden hours, the project team decided that section J (parent psychological well-being & stress) and section K (employment and educational activities) would be considered for deletion. These sections represent additional questions on the two most important areas of interest, as OMB notes, but are not of primary importance considering the other sections of the questionnaire. We do not believe that their removal would in any way jeopardize the most important questions in these areas, but their inclusion could make our findings more descriptive in areas of greatest interest to the policy and practitioner community.
In making this decision, it is important to note that we would not delete section B (depression symptomatology) or section C (treatment for depression) which are our primary measures to assess intervention impacts on mental health and treatment. Section J contains measures that assess parents’ expression of feelings and parenting stress, that while being important in gaining an overall picture of parenting well-being and we would prefer not to delete these items, are secondary in the analysis of the intervention’s impacts on mental health; primary being the rates of depression and whether respondents entered treatment.
In considering the deletion of section K (employment and educational activities), it is also important to note that we would not delete section L (employment history). Section L assesses current employment, history of employment, work hours, work schedule, wage, and work benefits. If faced with the decision to delete items, the project team would prefer to delete items concerning participation in job search and educational activities because at the 36-month point, it is less likely that the intervention will be continuing to affect these mediators of later employment outcomes.
1 Two additional assumptions are necessary to obtain unbiased results from this estimation strategy that we will also try to verify. First, the values of the independent variable X and the relation between independent variables and outcomes Y across individuals i are “stable” for those individuals (i.e., unaffected by variation in X or Y for others). In practice, this means that there are assumed to be no community effects or displacement effects. Second, the program effect δp on the independent variable of interest (i.e., the effect of Pi on Xi) is monotonic. This means that when δp > 0, (Xi|Pi=1) is greater than or equal to (Xi|Pi=0) for every person i. Thus, for example, if Pi is a training program and Xi is the amount of training received, no one would receive less training when randomly assigned to the training program than they would if they had not been assigned to the training program.
2 Benjamini, Yoav and Yosef Hochberg, “Controlling the False Discovery Rate: a Practical and Powerful Approach to Multiple Testing.” Journal of the Royal Statistical Society, 57(1): 289-300, 1995.
3 Darlington, Richard B. Regression and Linear Models. 1990. New York: McGraw-Hill Publishing Company
| File Type | application/msword |
| File Title | To: |
| Author | Jenny Au |
| Last Modified By | aguilar_b |
| File Modified | 2008-03-05 |
| File Created | 2008-03-05 |
© 2026 OMB.report | Privacy Policy