National Survey of S-L Survey OMB Justification - Part B
National Survey of S-L Survey OMB Justification - Part B.doc
National Survey of Community Service and Service-Learning in K-12 Public Schools
OMB: 3045-0126
OMB Forms Justification Package
National Study of the Prevalence of Community-Service and Service-Learning in K-12 Public Schools
PART B: COLLECTION OF INFORMATION EMPLOYING STATISTICAL METHODS
The Agency should be prepared to justify its decision not to use statistical methods in any case where such methods might reduce burden or improve accuracy of results. When Item 17 on OMB Form 83-1 is checked “Yes,” the following should be included in the Supporting Statement to the extent that it applies to the methods proposed:
Describe (including a numerical estimate) the potential respondent universe and any sampling or other respondent selection method to be used. Data on the number of entities (e.g., establishments, state and local government units, households, or persons) in the universe covered by the collection and in the corresponding sample are to be provided in tabular form for the universe as a whole and for each of the strata in the proposed sample. Indicate expected response rate for the collection as a whole. If the collection has been conducted previously, include the actual response rate achieved during the last collection.
The sample for the survey of the prevalence of community-service and service-learning will be drawn from the universe of elementary, middle and secondary public schools based on the Department of Education’s Common Core of Data (CCD) public school universe file, which is maintained by the National Center for Education Statistics (NCES). According the 2005-06 CCD, there were 87,419 public schools. From this universe, we will draw a nationally-representative sample of 2,000 schools ensuring an adequate representation of middle and high schools, as well as schools in low-income areas (based on percentage of students enrolled in the schools who are eligible for free or reduced price lunch). Within each instructional level, the sample will be stratified by poverty level of the schools (based on the proportion of eligible students who are eligible for free and reduced-price lunch) and size class (total enrollment) in rough proportion to the aggregate square root of the enrollment of the schools in the substrata. The use of the square root of enrollment will allow for greater selection probability for larger schools and, thereby, provide for greater precision for estimates based on student enrollment (e.g., the number of students in the school who are involved in service-learning).
The expected response rate for the sample is over 90 percent. This expected response rate is based on the response rates from the 1999 survey of 92 percent and the 2004 survey of 91 percent.
|
Sampling Frame, CCD 2005-06 |
Survey Sample |
||||||
Instructional Level |
No. of Schools |
% of Total |
No. of Students |
% of Total |
No. of Schools |
% of Total |
Est. Response Rate |
Est. Number of Responses |
Elementary |
51,947 |
59.4 |
23,211,083 |
48.0 |
1,099 |
55.0 |
0.90 |
989 |
Middle |
16,636 |
19.0 |
9,973,045 |
20.6 |
403 |
20.1 |
0.90 |
363 |
Secondary |
18,836 |
21.5 |
15,170,874 |
31,4 |
498 |
24.9 |
0.90 |
448 |
Total |
87,419 |
100.0 |
48,355,002 |
100.0 |
2,000 |
100.0 |
0.90 |
1,800 |
Describe the procedures for the collection of information including: (a) statistical methodology for stratification and sample selection, (b) estimation procedures, (c) degree of accuracy needed for the purpose described in the justification, (d) unusual problems requiring specialized sampling procedures, and (e) any use of periodic (less frequent than annual) data collection cycles to reduce burden.
A nationally-representative sample of 2,000 schools will be drawn from the 2005-06 CCD with stratification by instructional level (elementary, middle, and secondary), school poverty level (based on the proportion of eligible students, who are eligible for free and reduced-price lunch) and size class (total enrollment) in rough proportion to the aggregate square root of the enrollment of the schools in the substrata. The sample will include a slight overrepresentation of secondary and middle schools because of oversampling of larger schools. This sample allocation will allow for reliable national estimates and analysis while ensuring an acceptable level of precision at the overall level.
B.2.1 Sampling Frame
The sampling frame for the survey will be the NCES Common Core of Data (CCD) Public Elementary/Secondary School Universe Survey: School Year 2005-06 data file. The 2005-06 CCD is the most up-to-date file that is currently available. Only the regular schools will be included in the sampling frame. The special education schools, vocational schools, and other/alternative schools will be excluded from the sampling frame. The schools with a high grade of kindergarten or lower, ungraded schools, and schools in the outlying U.S. territories are ineligible for the survey and thus will be excluded from the sampling frame.
B.2.2 Stratification and Sample Allocation
The sampling strata will be formed by three instructional levels (elementary, middle, and secondary/combined), three poverty levels (based on the percentage of students enrolled in the school who are eligible for free or reduced-priced lunch: less than 25 percent; 25-54 percent; and 55 percent or more), and four school enrollment size classes. Table B.1 shows the number of schools in the sampling frame by the three stratification variables. Note that a small number of schools with unknown poverty level is placed in a separate stratum.
Table B.1. Number of Schools in the Sampling Frame by Instructional Level, Percent of |
||||||
Students Eligible for Free or Reduced-Price Lunch, and Enrollment Size Classes |
||||||
|
|
|
|
|
|
|
|
|
Percent of Students Eligible for Free or |
|
|||
|
|
Reduced-Price Lunch |
|
|||
|
Enrollment |
|
Less than |
25-54 |
55+ |
|
Instructional Level |
Size Class |
Missing |
25 percent |
Percent |
percent |
Total |
|
|
|
|
|
|
|
Elementary |
< 300 |
916 |
2,961 |
5,078 |
5,453 |
14,408 |
|
300-499 |
381 |
4,832 |
6,017 |
7,106 |
18,336 |
|
500-999 |
170 |
5,423 |
5,188 |
7,247 |
18,028 |
|
1,000+ |
8 |
299 |
266 |
602 |
1,175 |
|
Subtotal |
1,475 |
13,515 |
16,549 |
20,408 |
51,947 |
|
|
|
|
|
|
|
Middle |
< 300 |
148 |
748 |
1,540 |
1,224 |
3,660 |
|
300-499 |
119 |
840 |
1,379 |
1,233 |
3,571 |
|
500-999 |
109 |
2,319 |
2,672 |
2,118 |
7,218 |
|
1,000+ |
7 |
757 |
729 |
694 |
2,187 |
|
Subtotal |
383 |
4,664 |
6,320 |
5,269 |
16,636 |
|
|
|
|
|
|
|
Secondary/combined |
< 300 |
367 |
1,425 |
2,355 |
1,625 |
5,772 |
|
300-499 |
175 |
874 |
1,349 |
739 |
3,137 |
|
500-999 |
222 |
1,502 |
1,673 |
795 |
4,192 |
|
1,000+ |
96 |
2,639 |
2,114 |
886 |
5,735 |
|
Subtotal |
860 |
6,440 |
7,491 |
4,045 |
18,836 |
|
|
|
|
|
|
|
Total |
|
2,718 |
24,619 |
30,360 |
29,722 |
87,419 |
The total sample size of 2,000 is allocated to 48 sampling strata formed by the intersections of three stratification variables, in rough proportion to the aggregate square root of the enrollment of the schools in the stratum. The use of the square root of enrollment to determine the sample allocation is aimed at giving greater selection probabilities to larger schools within a given instructional level, and thus is expected to provide reasonably good sampling precision for estimates that are correlated with enrollment (e.g., the number of students in the school who are involved with service-learning or community service). As a result of oversampling larger schools, the middle schools and secondary schools are slightly oversampled because of relatively larger enrollment sizes in higher grades. Table B.2 shows sample allocation to sampling strata and Table B.3 shows the reciprocal of the sampling rates across the sampling strata.
Table B.2. Sample Sizes by Instructional Level, Percent of Students Eligible for Free or |
||||||
Reduced-Price Lunch, and Enrollment Size Classes |
|
|
|
|||
|
|
|
|
|
|
|
|
|
Percent of Students Eligible for Free or |
|
|||
|
|
Reduced-Price Lunch |
|
|||
|
Enrollment |
|
Less than |
25-54 |
55+ |
|
Instructional Level |
Size Class |
Missing |
25 percent |
Percent |
percent |
Total |
|
|
|
|
|
|
|
Elementary |
< 300 |
11 |
39 |
70 |
76 |
196 |
|
300-499 |
8 |
101 |
125 |
147 |
381 |
|
500-999 |
4 |
144 |
138 |
194 |
480 |
|
1,000+ |
0 |
11 |
9 |
22 |
42 |
|
Subtotal |
23 |
295 |
342 |
439 |
1,099 |
|
|
|
|
|
|
|
Middle |
< 300 |
2 |
10 |
20 |
16 |
48 |
|
300-499 |
2 |
18 |
29 |
26 |
74 |
|
500-999 |
3 |
65 |
74 |
58 |
200 |
|
1,000+ |
0 |
28 |
27 |
26 |
81 |
|
Subtotal |
7 |
120 |
149 |
126 |
403 |
|
|
|
|
|
|
|
Secondary/combined |
< 300 |
4 |
17 |
30 |
19 |
70 |
|
300-499 |
4 |
18 |
28 |
15 |
65 |
|
500-999 |
6 |
42 |
46 |
22 |
116 |
|
1,000+ |
4 |
113 |
91 |
39 |
247 |
|
Subtotal |
18 |
191 |
195 |
95 |
498 |
|
|
|
|
|
|
|
Total |
|
49 |
606 |
686 |
660 |
2,000 |
Table B.3. Reciprocal of the Sampling Rates by Instructional Level, Percent of |
|
||||
Students Eligible for Free or Reduced-Price Lunch, and Enrollment Size Classes |
|
||||
|
|
|
|
|
|
|
|
Percent of Students Eligible for Free or |
|||
|
|
Reduced-Price Lunch |
|||
|
Enrollment |
|
Less than |
25-54 |
55+ |
Instructional Level |
Size Class |
Missing |
25 percent |
percent |
percent |
|
|
|
|
|
|
Elementary |
< 300 |
83.6 |
76.3 |
72.6 |
71.5 |
|
300-499 |
48.8 |
47.8 |
48.2 |
48.2 |
|
500-999 |
38.4 |
37.6 |
37.7 |
37.3 |
|
1,000+ |
29.2 |
28.2 |
28.2 |
28.0 |
|
|
|
|
|
|
Middle |
< 300 |
82.4 |
74.4 |
77.6 |
77.0 |
|
300-499 |
48.1 |
48.0 |
48.2 |
48.1 |
|
500-999 |
38.4 |
35.7 |
36.1 |
36.3 |
|
1,000+ |
27.2 |
27.4 |
27.2 |
26.7 |
|
|
|
|
|
|
Secondary/combined |
< 300 |
92.8 |
82.3 |
78.5 |
85.4 |
|
300-499 |
48.5 |
48.4 |
48.5 |
48.8 |
|
500-999 |
36.7 |
35.7 |
36.3 |
36.3 |
|
1,000+ |
23.3 |
23.3 |
23.3 |
22.9 |
|
|
|
|
|
|
The schools within each sampling stratum will be stratified further in sample selection by an implicit stratification. This implicit stratification will be accomplished by sorting the records by type of locale (city, urban fringe, town, and rural) and by region within each sampling stratum and then drawing the sample systematically.
B.2.3 Sample Selection Method
The sample will be obtained by drawing an equal probability systematic sample of schools within each of the 48 strata defined by the instructional level, poverty level, and enrollment size classes. The sample selection will be independent across the strata. Within each stratum, the frame units will be placed in a sort order by type of locale, and within type of locale by region, and within region by school enrollment. This implicit stratification ensures the geographical dispersion among the sample schools and increases the probability that a range of school sizes within a stratum are selected.
B.2.4 Expected Precision of the Estimates
The domains of the population of interest for the survey are three instructional levels and three poverty levels for the schools (based on the percentage of students enrolled in the school who are eligible for free or reduced-priced lunch).
The
population parameters of interest are mainly in the form of
proportions--for example, percentage of schools using community
service and service-learning in each domain of interest and overall
in the U.S. An estimate of percentage of schools using
service-learning in poverty level h,
![]() will
be obtained as:
will
be obtained as:
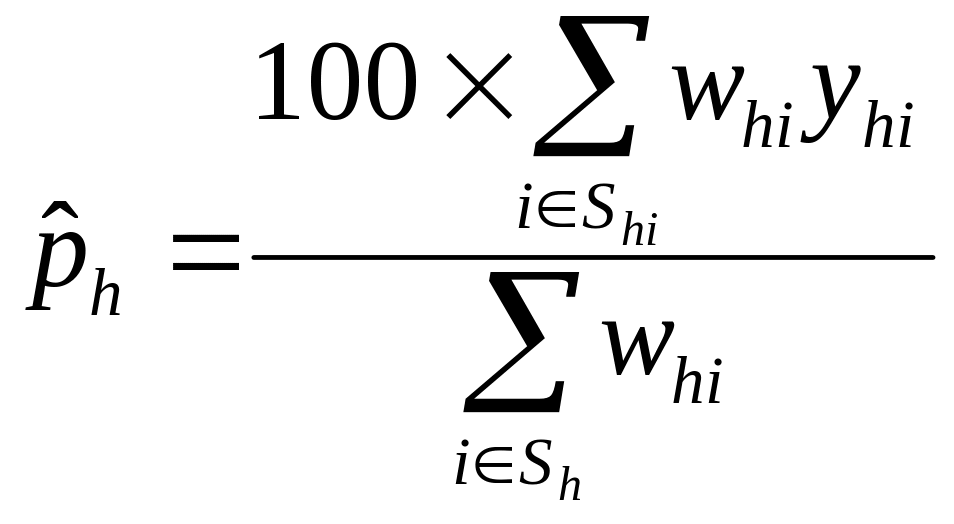
where,
Shi is the set of responding schools in poverty level h;
whi is the nonresponse adjusted sampling weight attached to responding school i in poverty level h (see the weighting section below for the derivation of the sampling weights);
yhi is the indicator of presence of service-learning in school i in poverty level h.
Table B.4 shows the expected precision levels for various percentages by domains of interest. The first column shows the domains. The second column shows the expected number of completed interviews (a 90 percent completion rate is assumed based on expected response rate of 91 percent and an ineligibility rate of about 1 percent). The third column shows the sample sizes reduced further by the design effect because of using differential sampling rates across enrollment size classes. The remaining columns show expected percentage errors for various levels of percent statistics. For example, for a 50 percent proportion for the elementary schools, which has an effective sample size of 915, the percent error will be around plus or minus 3.3 percent, with 95 percent confidence. As can be seen from Table B.4, the percent error is the largest for a 50 percent proportion and decreases as proportion moves further away from the 50 percent / 50 percent split. For example, for a 20 percent / 80 percent split, the error is 2.6 percent for elementary schools.
Table B.4. Expected Number of Completed Interviews, Effective Sample Size, and Percent |
|||||
Error1/ for Various Estimated Percentages by Major Domains of Interest and Overall |
|
|
|||
|
|
|
|
|
|
|
Expected |
Effective |
|
|
|
|
Number of |
Sample |
Percentages |
||
Domains |
Completes |
Size |
50/50 |
30/70 |
20/80 |
|
|
|
|
|
|
|
|
|
|
|
|
Total Sample |
1,800 |
1,586 |
2.5 |
2.3 |
2.0 |
|
|
|
|
|
|
|
|
|
|
|
|
Instructional Level |
|
|
|
|
|
Elementary |
989 |
915 |
3.3 |
3.0 |
2.6 |
Middle |
363 |
322 |
5.6 |
5.1 |
4.5 |
Secondary/combined |
448 |
350 |
5.3 |
4.9 |
4.3 |
|
|
|
|
|
|
|
|
|
|
|
|
Percent of Students |
|
|
|
|
|
Eligible for Free or |
|
|
|
|
|
Reduced-Price Lunch 2/ |
|
|
|
|
|
Less than 25 |
559 |
489 |
4.5 |
4.1 |
3.6 |
25-54 percent |
632 |
558 |
4.2 |
3.9 |
3.4 |
55 percent or more |
609 |
546 |
4.3 |
3.9 |
3.4 |
|
|
|
|
|
|
|
|
|
|
|
|
Notes: 1/ Percent errors are obtained by multiplying expected standard errors by 2. |
|||||
2/ Sample schools with missing poverty level data are distributed proportionately |
|||||
to known poverty levels. |
|
|
|
|
|
There is an interest in comparing proportions across the domains--for example, to compare the proportions of schools using service-learning between the low and high poverty school domains. The sample sizes in the domains should be large enough to provide more than 80 percent power for the statistical tests to detect reasonable differences in proportions. The power of a test is the probability of rejecting the null hypothesis of no difference between two proportions, when the null hypothesis is false and the alternative hypothesis is true. If the power of the test is inadequate, when the null hypothesis of no difference is not rejected, we can not conclude with a reasonable confidence that there is no difference between the proportions because this may be due to the fact that the sample size is too small to detect the difference. A power of 80 percent is generally considered as adequate. Given, a certain power level, larger sample sizes are needed to detect smaller differences. Table B.5, shows power of a test for the various differences between two proportions with the low and high poverty domains effective sample sizes from Table B.4, and with a significance level of 0.05. The power is shown for various sizes of differences and for various magnitudes of proportions. For example, a difference size of 8 percent will be detected with 80 percent power when average of two proportions is 30 percent (for example, the proportions for low and high poverty domains are 34 and 26 percent, respectively). For proportions with larger magnitudes, only larger differences can be detected with the same power given the same sample sizes. For example, when average of the proportions is about 50 percent only a difference size of 9 percent can be detected with over 80 percent power with these sample sizes. Thus, the poverty level domains effective sample sizes are adequate to detect size differences of 9 percent (or larger) between percentages of any magnitude with more than 80 percent power.
Table B.5 Power of a Test for Difference in Proportions of Two domains with effective |
|||||
Sample sizes of Low and High Poverty Domains by various averages and differences of two proportions |
|||||
Sampling is independent across the domains |
|
|
|
||
Significance level is 0.05 |
|
|
|
|
|
|
|
|
|
|
|
Average of two |
Difference of two proportions (%) |
||||
proportions (%) |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
50 |
0.49 |
0.62 |
0.73 |
0.83 |
0.90 |
40 |
0.51 |
0.64 |
0.75 |
0.84 |
0.91 |
30 |
0.56 |
0.69 |
0.80 |
0.89 |
0.94 |
20 |
0.68 |
0.81 |
0.90 |
0.95 |
0.98 |
|
|
|
|
|
|
|
|
|
|
|
|
B.2.5 Sampling Weights and Variance Estimation
The sampling weights will be attached to every eligible school record with a completed interview (1) to account for differential probabilities of selection and (2) to reduce the potential bias resulting from nonresponse. Each sample school with a completed interview will be assigned a final weight.
Initially, we will assign a base weight to each sample school record as the reciprocal of the probability of its selection. The base weights will then be adjusted for nonresponse in order to reduce potential biases resulting from not obtaining an interview with every school in the sample. These adjustments will be made by redistributing the weights of nonresponding schools to responding schools with similar propensities for response. A predictive model for response propensity will be developed to identify subgroups of population with differential response rates. These subgroups will then be used as nonresponse adjustment cells and a separate weight adjustment will be applied in each cell. The potential predictors that can be used in this modeling effort have to be known for both respondents and nonrespondents. These include instruction levels, proportion of students eligible for free or reduced-price lunch, enrollment size classes, type of locale, and region.
If response propensity is independent of survey estimates within nonresponse adjustment cells, then nonresponse-adjusted weights yield unbiased estimates. There are several alternative methods of forming nonresponse adjustment cells to achieve this result. We plan to use Chi-Square Automatic Interaction Detector (CHAID) software (SPSS, 19931) to guide us in forming the cells. CHAID partitions data into homogenous subsets with respect to response propensity. To accomplish this, it first merges values of the individual predictors, which are statistically homogeneous with respect to the response propensity and maintains all other heterogeneous values. It then selects the most significant predictor (with the smallest p-value) as the best predictor of response propensity and thus forms the first branch in the decision tree. It continues applying the same process within the subgroups (nodes) defined by the "best" predictor chosen in the preceding step. This process continues until no significant predictor is found or a specified (about 20) minimum node size is reached. The procedure is stepwise and creates a hierarchical tree-like structure.
Although nonresponse adjustment can reduce bias, at the same time, it may increase the variance of estimates. Small adjustment cells and/or low response rates (or large nonresponse adjustment factors) may increase the variance and give rise to unstable estimates. In order to prevent an unduly increase in variance and thereby an adverse effect on the mean square error of the estimates, we plan to limit the size of the smallest cell to a minimum and avoid large adjustment factors.
B.2.6. Variance Estimation
The estimates of standard errors in this survey can be obtained using a variance estimation software, such as SAS-callable SUDAAN or WesVar. SUDAAN provides variance estimation procedures using both Taylor series linearization method and replication methods. WesVar uses only replication methods. The replication method requires the development of a replication scheme and computation of the replicate weights. We propose to use SAS-callable SUDAAN with the Taylor linearization procedure, which requires less effort to obtain the standard errors of the survey estimates. The estimators in this survey are in the form of totals, means, and proportions. A Taylor linearization approach is appropriate to use with these types of estimators.
Describe methods to maximize response rates and to deal with issues of non-response. The accuracy and reliability of information must be shown to be adequate for intended use. For collections based on sampling, a special justification must be provided for any collection that will not yield “reliable” data that can be generalized to the universe studied.
Data collection will incorporate a multi-layered process to maximize response rates and deal with issues of non-response. A pre-notification letter explaining the purpose of the survey will be sent to the school district superintendent of all schools in the sample to cultivate cooperation in advance. Included will be a copy of the survey, and a list of the specific schools selected in that district. Then the survey will be mailed to all school principals in a package that will include a letter to the principal explaining the purpose of the survey, a copy of the pre-notification letter, a list of frequently asked questions, and a prepaid business reply envelope. The principal will be instructed to refer the survey to the individual most knowledgeable about service-learning activities within the school. The respondents will be allowed two weeks for completing and returning the survey. Telephone follow-up calls will be made by trained interviewers to those schools that have not responded, as well as those schools that submitted surveys that are incomplete or contain unclear or incongruous responses. Respondents will be given the opportunity to complete the survey by telephone.
A receipt control system will be used to track the completion of surveys. A unique 8-digit identification number will assigned to each school in the tracking system. This same identification code will be affixed to the survey instrument and return envelopes to ensure accuracy in disposition codes and data entry. Updated disposition codes will be compiled at the end of each working day to identify outstanding surveys, surveys with missing data and the contact status with schools.
The above data collection methods were successfully used during the 2004 survey to achieve a 91 percent response rate. The methods are also similar to those used by NCES’s Fast Response Survey System, which achieved a 92 percent response rate for a similar survey in 1999.
Describe any tests of procedures or methods to be undertaken. Testing is encouraged as an effective means of refining collections of information to minimize burden and improve utility. Tests must be approved if they call for answers to identical questions from 10 or more respondents. A proposed test or set of tests may be submitted for approval separately or in combination with the main collection of data.
All of the questions included in the survey have been previously tested, either in earlier national surveys of the prevalence of community service and service-learning conducted in 1999 and 2004 or in the annual survey of Learn and Serve America grantees, subgrantees and sub-subgrantees. In addition, the methodology that will be used in implementing the survey is based on the methodology that was used in the 2004 survey of K-12 schools. No additional tests will be conducted.
Provide the name and telephone number of individuals consulted on statistical aspects of the design and the name of the agency unit, contractor(s), grantee(s), or other person(s) who will collect and/or analyze the information for the agency.
The data will be collected and initial analysis conducted by Westat, 1650 Research Boulevard, Rockville, MD 20850-3195. The Project Director for Westat is Cynthia Robins, 301-738-3524.
1SPSS (1993), SPSS for Windows: CHAID, Release 6.0, User’s Guide, Jay Magidson/SPSS Inc., 1993.
| File Type | application/msword |
| File Title | OMB Forms Justification Package |
| Author | STRANG_B |
| Last Modified By | kcramer |
| File Modified | 2007-12-20 |
| File Created | 2007-12-14 |
© 2026 OMB.report | Privacy Policy