AMSTI_OMB_Supporting_Statement_B_Revised_050307.FINAL-2
AMSTI_OMB_Supporting_Statement_B_Revised_050307.FINAL-2.doc
The Effectiveness of the Alabama Mathematics, Science and Technology Initiative (AMSTI)
OMB: 1850-0831

omb package
2.1.3: The Effectiveness of the Alabama Mathematics, Science and Technology Initiative (AMSTI)
Supporting Statement Part B
Date Submitted:
May 9, 2007
Contract Number:
ED-06-CO-0028
Submitted to:
Gil Garcia
Institute of Education Sciences
U.S. Department of Education
Submitted by:
Ludwig D. van Broekhuizen
REL-Southeast
SERVE Center
915 Northridge Street, Second Floor
Greensboro, NC 27403-2112
(800) 755-3277
(336) 315-7400
TABLE OF CONTENTS
OMB Package Supporting Statement B
Potential Respondent Universe and Any Sampling Selection Method to be Used 3
1.1 Potential Universe and Sampling Selection 3
Power analyses for measuring impacts within student subgroups 11
Procedures for Collection of Information 13
Methods to Maximize Response 14
Tests of Procedures or Methods 15
Supporting Statement for Request for OMB Approval of Data Collection/Needs Assessment for the REL-SE
Part B. Collections of Information Employing Statistical Methods
Describe (including a numerical estimate) the potential respondent universe and any sampling or any other respondent selection methods to be used. Data on the number of entities (e.g., establishments, State and local government units, household, or persons) in the universe covered by the collection and in the corresponding sample are to be provided in tabular form for the universe as a whole and for each of the strata in the proposed sample. Indicate expected response rates for the collection as a whole. If the collection has been conducted previously, include the actual response rate achieved during the last collection.
1.1 Potential Universe and Sampling Selection
The universe of cases for the original study is defined as all Alabama public schools with at least one grade of fourth through eighth in the three regions that are beginning to receive the AMSTI intervention in Year 1 (2006-2007), along with all classrooms, teachers, and students in those schools at these grade levels in Year 1. The regions are each defined by their MASTER site; the three MASTER sites are the University of Alabama-Montevallo, the University of Alabama-Tuscaloosa and Troy University. These regions were chosen for the study based on practicality, that is, these regions were offered AMSTI for the first time in school year 2006-2007. Within these three regions, all 382 existing public schools were invited to apply for AMSTI participation. Of these, 106 schools applied for AMSTI, from which, a convenience sample of 40 schools was selected. The 40 schools were then paired on the basis of grade configuration, math scores, percent of students qualifying for free lunch, and the percent of minority students. Schools with only grades K-3 or 9-12 were excluded, as well as a small number that had previously been accepted into AMSTI before the random assignment process for the study could be set up. A coin toss determined which school in the pair would receive the AMSTI intervention, the other school going into the control group.
We used a multi-stage approach where we paired schools based on the variables that we thought most relevant. Schools were paired first on the basis of similarity of grade configuration, then math scores, then percent of minority students, and finally (when possible) on percent of low income students. We did not identify pairs using a statistical method such as a data reduction procedure whereby schools are situated along a single principle component derived from the various criteria on which we matched. We believe that we matched on factors that matter and that our more heuristic approach is sound. For an explanation of the implications of the matched pairs design for the power analysis, please refer to section 1.2.
Within the 40 schools, there were approximately 174 treatment teachers, 150 control teachers, 6,565 treatment students and 5,568 control students in the relevant grade levels (4-8) during the 2005-06 school year. These represent the potential universe for data collection. Table 1 details the participant numbers and the selection methods for the study as a whole and for each type of data collection.
The participants for the replication study will be selected in the exact same manner from the Jackson State University and the Wallace regions, which are slated to begin receiving the AMSTI intervention in 2007-2008.
Table 1
Sampling Selection Methods
Universe of Available Cases |
Number to be Selected |
Selection Method |
Expected Response Rate |
|
|
382
|
40 Treatment – 20 Control – 20 Grade 4 – 21 Grade 5 – 26 Grade 6 – 23 Grade 7 – 22 Grade 8 – 18
174 150 |
Purposive: Grades K-3 and 9-12 excluded plus those previously selected for AMSTI. Then within each region schools were selected based on their similarity to regional demographics.
Random selection of treatment vs. control schools from among the 40.
All math and science teachers in grades 4-8. |
100%
At least 90% At least 90% |
Professional Development observations/trainer logs |
52 |
17
|
The sample consisting of all trainers from three regions assigned to math and science at grade levels 5 and 7 were selected to account for the overall quality of training provided by the region. |
100%
|
Professional Development Participant Survey |
324 |
210
|
Universe of all teachers of grade 5 and grade 7 math and science [4 per school x 20 schools] who attend the training. Grade 5 and 7 teachers were selected to correspond to the sample of trainers and to correspond to the grade levels where both science and mathematics achievement data are available. |
At least 90%
|
AMSTI Study Teacher Classroom Observations |
324
|
42 (20 AMSTI and 20 control schools plus 2 additional teachers) |
Teachers will be chosen at random from a stratified sample (seven strata: grades 4, 5, 6, 7, and 8 math, grades 5 and 7 science) so that data are generalizable to all math grades and grade 5 and grade 7 science teachers and correspond to student achievement, trainer log and training participant data. |
At least 90%
|
Teacher interviews |
Year One |
84 (observed teachers plus a stand alone teacher in each AMSTI and control school) |
Teachers will be chosen at random from a stratified sample (seven strata: grades 4, 5, 6, 7, and 8 math, grades 5 and 7 science) so that data are generalizable to all math grades and grade 5 and grade 7 science teachers and correspond to student achievement, trainer log and training participant data. |
At least 90% |
Principal interviews |
Year One
|
40
|
It is necessary to sample the universe of principals in AMSTI and control schools to determine level of implementation in each of the schools in the study. |
At least 90% |
We will use statistical methods appropriate for the analysis of group randomized trials. These include, but are not limited to, analysis of covariance and hierarchical linear modeling. Methods will be geared to measuring differences between treatment and control schools in terms of student- and teacher-level outcomes.
The techniques will reflect three general types of analyses. The first will compare the performance of students in the two conditions each year within each grade level. We will compute mean differences and adjust the standard error to account for the clustering of students in upper-level units. The second will compare growth trajectories over time for individuals in the two conditions. Piecewise growth models will be used for this. The third will look at changes over time within a grade-level.
We will perform both combined and subgroup analyses. The subgroups are identified at the student- and teacher-levels (i.e., below the level of randomization.) This allows us to subdivide the sample and do these analyses without compromising statistical power.
Outcomes will be measured across several grade-levels. For student outcomes, if scales are not vertically aligned, we will perform separate analyses within each grade level and then combine results after transforming the effect estimates so that they are on a common scale (e.g., in terms of standard deviation units).
We will not perform analyses by region or school-type. Instead, we will do a combined analysis that will yield an estimate of the average impact across regions. AMSTI is designed so that each classroom, school, and region adapts the program to fit local needs, while still adhering to the program’s guidelines and requirements. Measures of implementation fidelity will look at regional differences. However student achievement data will be analyzed only at the level of the three original regions combined at the end of the first year, and then reanalyzed to include all five regions in both replications combined at the end of the second year.
Schools are the unit of randomization, and in the following section we show the results of a power analysis where we estimate that 66 schools will be required to detect an effect size as small as .15 in student-level outcomes. To compute this value we consider the mean impact of the intervention following the first year. That is, we consider what the impact will be of AMSTI versus no AMSTI. To answer this question, half the schools will be randomly assigned to the treatment condition and the other half to the control condition. It is important to note that in the power calculation, the number of teachers per school (J=8) and the number of students per teacher (n=35) is assumed fixed. That is, these values contribute to the determination of the school sample size and are not themselves determined through the power analysis.
We are also interested in determining whether the Year Two impact is greater than the Year One impact; that is, whether there are greater gains for the cohort of students that experiences AMSTI after it’s already been in place in a school for a year. The sample size for this will be larger, since, within each replication, we will have the opportunity to test this question twice: once for AMSTI1 and once for AMSTI2. That is, we will compare the performance of AMSTI1 schools (those receiving AMSTI the first year) after the first year to outcomes from the same schools after the second year; we will also compare the performance of AMSTI2 schools (those receiving AMSTI the second year) after the second year to outcomes from the same schools after the third year. This doubles the available sample size; however, it also tries to detect a potentially smaller effect (i.e., the gain due to AMSTI between the first and second year of implementation). It is also possible, however, that a discernable treatment impact will be observed only after the second year of implementation (after a ‘burn-in period’ during which the institution adapts to the intervention) in which case we would have a larger sample picking up a larger effect (compared to the sample available for comparing AMSTI versus no AMSTI in the first year).
Power for Detecting the Impact of AMSTI on Student Outcomes After the First Year of the Intervention
We will be assessing the following student outcomes: student achievement in math, science and reading. Analysis will include sub-test outcomes in order to determine both the extent of impact on student achievement in areas that align with the AMSTI goals, such as higher-order thinking skills, and the extent of impact on student achievement in other areas that matter to student progress in science and math.
The power analysis is performed assuming that students from across all grade levels are included in one impact analysis. AMSTI scores are vertically equated across the grade-levels of interest. We were assured of this through a direct telephone conversation with Harcourt. This allows us to analyze student-outcomes simultaneously across grade-levels. We do not have information to indicate that we should expect heterogeneity in the treatment impact across grades which would be the main motivation for doing grade-specific analyses. In order to test our assumption that it is appropriate to pool data across grades 4 through 8, researchers compared the survey data of elementary school principals with the data of middle school principals. We administered t-tests on all of the numeric data from the web-based principal survey that was administered in August, 2006 (see Section 3.1.8). Only 1 out of 40 t-tests resulted in a significant difference (p<.05) in the survey answers of the two groups. Based on these results, researchers feel confident that pooling across these grades is appropriate for this study.
Scores are also horizontally equated, which will allow us to include scores from across the replication studies in a single analysis. We emphasize that although in science we can only collect data in 5th and 7th grades, the number of randomized units (i.e., schools) stays the same, so power is not adversely affected. Assuming a roughly equal number of students at each grade level, the student sample for the analysis of science outcomes drops to 40%. (In the section below, where we consider sample size requirements for subgroups, we show that about 70 schools are required to analyze the impact of the intervention in the case where only 40% of the original sample of students is available.)
In computing the sample size necessary to detect a potential impact of AMSTI on average student performance, we faced the problem of deciding whether to treat the design as having two or three levels. The advantage of considering a two-level design is that parameter estimates for this design have been explored previously in both reading and mathematics for the grade levels that are relevant to the AMSTI experiment (Hedges & Hedberg, 2006). There is no precedent that shows how variance should be partitioned among three levels (schools, teachers and students) for the outcome being considered. Also, there is a track record of experiments that have been performed in the past where schools were at level-2 and students at level-1 (e.g., Borman & Hewes, 2002). Furthermore, in at least one simulation study, uncertainty in the estimated treatment impact did not depend much on whether random effects were modeled for the mid-level in a three-level design (Schochet (2005), citing Murray (1996)) so long as mid-level covariates were not included in the model. Given these points, we computed the number of schools required for a two-level design with students at level-1 and schools at level-2 (where we are concerned with the impact on student scores).
We used the program Optimal Design (Raudenbush, Spybrook, Liu, & Congdon, 2006) to perform the power analysis. The work by Hedges and Hedberg (2006) shows that for a heterogeneous sample of schools the unconditional intraclass correlation (ICC) for reading outcomes in grade 4 through grade 8 ranges between .174 and .263. For math outcomes, the range is between .185 and .264. In the power analysis we set this value to .220. Prior work (Bloom, 2005b) that looks at the effects of adding school-level covariates (specifically, average prior score values) to impact analyses, suggests an R-squared value of .64.
We assume that the smallest educationally significant effect size will be .20 (Given lack of information about plausible values for the effect size, we adopt a standard based on our belief that an effect size that is smaller than this is unlikely to have an educationally important impact.) However, as a result of using a matched-pairs design, we show below that we will be able to detect an effect size as small as .15. Put another way, in the power analysis that we perform below (using the Optimal Design software) we assume an effect size of .20, but the sample size computed may be enough to detect an even smaller effect, given that we used a matched-pairs design. In the power analysis we set the type 1 error rate at .05. The number of students per school is fixed at n=280 (8 teachers per school times 35 students per teacher). Assuming these parameter settings, we computed the following curve showing power as a function of the number of schools required. (We remind the reader that this power analysis is concerned with student-level outcomes.)
Figure 2.
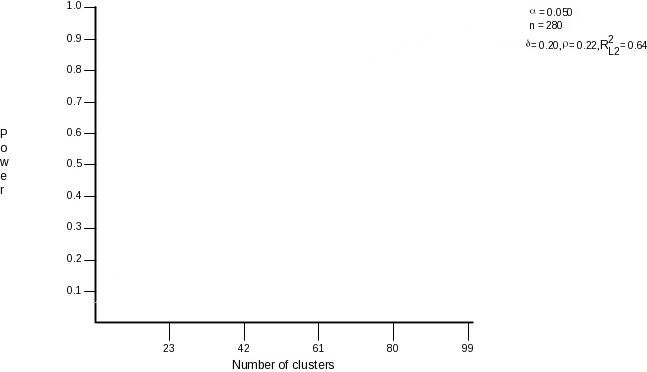
We see that 66 schools are required to detect an effect size of .20, assuming type-1 and type-2 error rates of .05 and .20, respectively, and assuming an intraclass correlation of .22.
This result demonstrates the need for the proposed replication study, which will increase our total school sample size from 40 to 80. As was described in the proposal, the first-year study, which begins in 2006-2007 includes 40 schools. The second year replication study will involve an additional 40 schools, thereby raising the total sample size to 80, which surpasses the 66 required and is a more than adequate number even if 10% of schools drop out of the study.
We will proceed to analyze the results of the first replication once the data are in, with the caveat that the MDES will be approximately .27 (we computed this result using the same parameters as in the power analysis above, but with the school sample size lowered to 40.) Once the results from the replication study are in, we will reanalyze the results with all schools included. We will add a variable into the analysis to indicate which replication a school is participating in, in case there is a significant change in overall performance from one replication to the next.
The ODS program figures in the effect of losing one degree of freedom when adding the prior score covariate into the computation of the required sample size.
In our power analyses, we did not compute the effect on precision of using a matched-pairs design. Bloom (2005) describes the change in MDE that results from using a pairing strategy. When pair-wise matching is done with respect to a single school-level baseline characteristic, and R-squared is the predictive power of that covariate (independent of other covariates) in a regression of the school-level outcome against that covariate, then the ratio of MDE with and without pairing is:
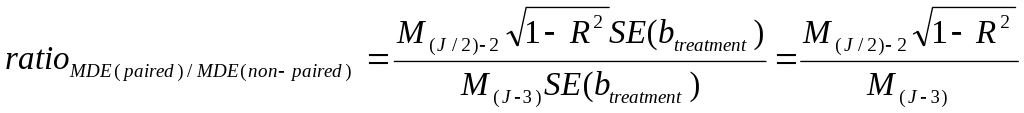
M is the minimum effect multiplier, and J is the number of upper-level units (schools). (We modify Bloom’s original formulation slightly by subtracting-off the additional degree of freedom used to compute the effect of adding a prior score covariate into the power calculation.)
Importantly, because we powered for the situation where a prior score covariate is included in the analysis, and we believe that this covariate will account for 64% of the variance in the outcome, matching must improve on this improvement. The R-squared presented above is therefore the proportion of variance that remains to be explained after conditioning on the prior score covariate (i.e., it is a proportion of the variance in the residuals after conditioning on the prior score.)
Complicating the picture is the fact that we matched schools on a variety of covariates (i.e., on a dimension that is a composite of many characteristics.) We believe that the criteria we used to match schools on were sufficiently unrelated to the prior score and sufficiently important to predicting the outcome that they would account for 50% of the residual variance. 1
Under this assumption, we have:
![]()
For a two-tailed test, M is defined as:
![]() ,
where D is the degrees of freedom
,
where D is the degrees of freedom
For J=66 schools we compute the gain in precision resulting from using matched pairs as:
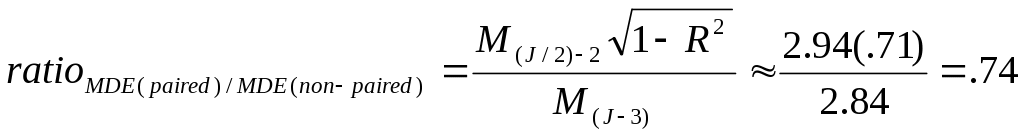
This shows that in order for the loss in precision due to the loss of degrees of freedom to outweigh the gain due to matching, the following must hold:
![]()
![]()
In other words, only
if
![]() goes below .08 will the precision lost due to loss of degrees of
freedom be greater than the precision gained through using a matched
pairs design.
goes below .08 will the precision lost due to loss of degrees of
freedom be greater than the precision gained through using a matched
pairs design.
This also means that as a result of using a matched-pairs design, the MDES will be smaller than the .20 that was specified in the previous power analysis. The number of units required is therefore conservative. With pairing, for the same sample size we can pick up an effect as small as .74*.20=.15 standard deviation.
As explained above, we followed the approach of other peer reviewed and published studies in going with a two-level power analysis. However, we also explored the effects of ignoring a mid-level such as the classroom level. Below we consider, from a theoretical perspective, the effect on precision of assuming that the ICC reflects the proportion of total variance NOT attributable to student-level differences (as opposed to assuming that the ICC reflects the proportion of total variance attributable to school-level differences.)
The standard error for the estimated treatment impact, in the case of a three level model, is proportional to the quantity:
![]()
(many sources describe a version of this equation, including Bloom (2005)). This is for a simple impact model without the prior score covariate.
![]() is
the variance for the error component at level-3
is
the variance for the error component at level-3
![]() is
the variance for the error component at level-2
is
the variance for the error component at level-2
![]() is
the variance for the error component at level-1
is
the variance for the error component at level-1
J, K and n are the number of level-3 units, the number of level-2 units per level-3 unit, and the number of level-1 units per level-2 unit, respectively.
If the ICC reflects the proportion of total variance attributable to school-level differences then we write it as:
![]()
If the ICC reflects the proportion of total variance NOT attributable to student-level differences then we write it as:
![]()
The question is: what’s the detriment to assuming that all the variance NOT attributable to student-level differences is attributable to schools (when only some of it is attributable to schools and the rest is attributable to levels below the school-level)?
Moving all the variance not attributable to students to the school level results in the following expression:
![]() ,
,
This is distinguished from the correct expression:
![]() .
.
We note that:
![]()
This means that we end up powering the experiment to detect an effect with an SE that is larger than the true SE. MDES is proportional to SE, so we will overestimate MDES. For instance, if MDES is .20, the MDES we compute will be some value greater than .20. This means that when we power our study to detect an effect of .20, the study will in fact be powered to detect a smaller effect than that (for set levels of type-1 and type-2 error.) Assuming that all the variability above the student level is at the level of schools will result in a conservative estimate of the number of units required.
Power Analyses for Measuring Impacts within Student Subgroups
We will assume that there are subtypes of each kind of student in each school, so subgroup analyses for students don’t involve a reduction in the number of units of randomization (i.e., in the number of schools.)
In the original proposal we identified several student subgroups of interest including: students on free or reduced price lunch, students of specific ethnicity, students who are disabled and English language learners. Demographic data from Alabama indicate that 49% of students are low-income and 36% are minorities. The proportion disabled is expected to be even smaller. We computed the schools sample sizes required when student subsamples drop to 49%, 36% and 10%. The last of these is meant to account for a possible analysis involving a particularly small subgroup of students.
We decided to hold the other parameter settings constant. It is not clear how the parameters will change when the student sample is restricted. Usually, more homogeneous subsamples lead to lower ICCs, which means that there is a proportionately larger between-school reduction in variance than a within-school reduction in variance. However, limiting the samples of students in schools will also limit the distribution of school-mean pretest scores which may decrease R-squared. Decreasing the ICC will decrease the MDES, but decreasing R-squared will increase MDES. Given lack of information about such trade-offs, but knowing that these values will trade off, we felt it reasonable to make the assumption that the net effect of these changes of parameters may be small.
We computed the following required sample sizes for detecting an effect size of .20, assuming type-1 and type-2 error rates of .05 and .20, respectively, and assuming an intraclass correlation of .22:
Keeping in 49% of the student sample leads to a school sample size requirement of 68.
Keeping in 36% of the student sample leads to a school sample size requirement of 70.
Keeping in 10% of the student sample leads to a school sample size requirement of 90.
From this we see that student subgroup analyses will have to await the results of the replication study in order to get a sufficient number of schools to detect an effect size of .20 at conventional levels of type-1 and type-2 error. As with the entire sample, we will conduct student subgroup analyses after the first year using the results of the first replication, with the caveat that the MDES will be larger than .20.
We point out however, that we will not have the power to detect effects of size .20 standard deviation when student subgroups are very small even with data from both replications (e.g., in the case of the third bullet above, where we use only 10% of students, we would need 90 schools.)
Power for Detecting the Impact of AMSTI on Teacher Outcomes After the First Year of the Intervention
When addressing teacher outcomes we point out again that the number of teachers per school is fixed (i.e., 8 teachers per school). The question then is, how many schools are needed to detect the impact of one year of AMSTI on teacher outcomes.
We will be assessing the following teacher outcomes:
Content knowledge
Use of materials
Hours teaching math and science
Hours of inquiry-based instruction
Hours teaching higher-order thinking skills
Hours of hands-on instruction
Making connections with students’ out of school experiences
Making connections with other disciplines
Assessment of student learning
We conducted a two-level power analysis to answer this question. We cannot justify adding more schools to the experiment just to adequately power a study of teacher outcomes (as compared to student outcomes, which are of primary interest).
For this reason, rather than reporting the number of schools required, we compute the minimally detectable effect size for teacher outcomes given the number of schools that are available (40). We assume pre-post correlations in school means of teacher-level outcomes to be .80 .
Results are shown in the following table and corresponding graphs:
alpha |
power |
J |
n |
R-squared |
ICC |
MDES |
.05 |
80% |
40 |
8 |
.64 |
.05 |
.34 |
.05 |
80% |
40 |
8 |
.64 |
.10 |
.36 |
.05 |
80% |
40 |
8 |
.64 |
.20 |
.39 |
Figure 3.
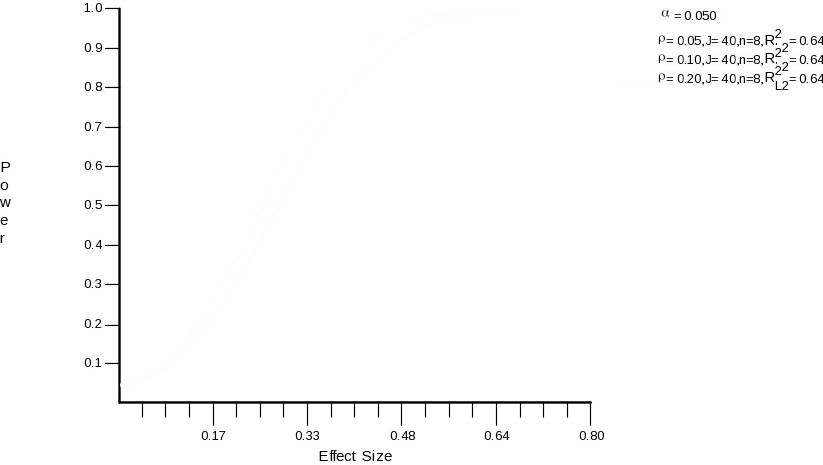
A change in ICC and in the R-squared does not make a large difference to the MDES given the available sample sizes. Also, we expect that the MDES will be slightly smaller than the ones computed here because we are using a matched pairs design, which effectively lowers the ICC. If the composite dimension on which we matched accounts for about 50% of the variance in teacher-level outcomes, then consistent with the calculation in the previous section, this will lead to approximately a 25% reduction in MDES
Describe procedures for collection of information, including: statistical methodology for stratification and sample selection; estimation procedures; degree of accuracy needed for the purpose described in the justification; unusual problems requiring specialized sampling procedures; and any use of periodic (less frequent than annual) data collection cycles to reduce burden.
Much of the data collection will cover the full universe. Teacher data, in the form of surveys, are to be collected on all 324 teachers. All principals will be surveyed and interviewed at each of the 40 schools. For parts of the implementation study, however, classroom observations and interviews will involve only a sample of the teachers.
Training data will be collected for each region by having all Summer Institute trainers of fifth grade math, fifth grade science, seventh grade math and seventh grade science complete logs indicating what they covered each day and how they were covering it. Their session participants will each complete a pre-post retrospective survey to assess knowledge, skill, and confidence gains relative to receipt of the training. Portions of sessions for each of these four training groups will also be observed. In the case of one region, Montevallo, the high numbers of session participants required two additional trainers, and while the additional sessions will not be observed, the logs and participant surveys will be completed. Because data will be collected for each of the three regions, results can be aggregated to the region level.
Another sub-sample will be used to conduct teacher observations and interviews. Each region will be broken into seven strata: fourth grade math, fifth grade math, sixth grade math, seventh grade math, eighth grade math, fifth grade science and seventh grade science. Separating teachers into the different strata is important because the impact analyses will be conducted separately for each grade and subject, and there are test scores available only for these seven grades/subjects. Stratifying into seven groups will thus make it possible to match implementation information to test score data. Stratifying by region was selected to ensure that each region was covered, thus taking into account the possibility that implementation may vary by region. Because teachers within a given stratum will be chosen at random, it can be assumed that, on average, the 21 observed teachers are representative of instructional practice in the three regions. The data collection will be as follows: In the AMSTI schools, 21 teacher/classroom observations and interviews with those teachers observed will be conducted in the 20 schools (1 in 19 schools; and 2 in 1 school). This will allow for three observation/interview data points for each of the seven strata. In addition, another 21 “stand alone” interviews will be conducted with other teachers (not observed) to provide for an additional three interview data points for each of the seven strata. The same sampling procedure will be used to select 21 teachers for observations and interviews, and another 21 teachers to complete the “stand alone” interviews in the 20 control schools. Copies of the data collection instruments and consent forms are provided in appendices A through X.
Describe methods to maximize response rates and to deal with issues of non-response. The accuracy and reliability of information collected must be shown to be adequate for intended uses. For collections based on sampling, a special justification must be provided for any collection that will not yield “reliable” data that can be generalized to the universe studied.
Efforts to maximize response are extensive. Training participants first meet researchers at their summer training where they are introduced to the study and given the opportunity to ask questions. Principals then receive an e-mail followed by a telephone call, further providing them the opportunity to learn more about the study and ask questions or voice concerns. Once principals have signed consent forms, their teachers receive an informational e-mail containing contact information so that they may learn more about the study and ask questions of researchers. Then teachers meet within their schools to again discuss the study and to sign consent forms. Invitations to the web-based surveys are e-mailed to each teacher and principal. Non-respondents receive first an e-mail and then phone calls in order to assure acceptable response rates.
Prior to the observations and interviews, staff will contact principals and selected teachers by phone or e-mail. The principals and teachers will be provided with information about the purpose and procedures for the observations and interviews. Also at this time, researchers will work out a schedule for classroom visits, ensuring these visits take place during a time that is convenient to the teacher and principal, and during a time when AMSTI teachers will be conducting lessons using the AMSTI materials and kits.
Describe any tests of procedures or methods to be undertaken. Testing is encouraged as an effective means of refining collections of information to minimize burden and improve utility. Tests must be approved if they call for answers to identical questions from 10 or more respondents. A proposed test or set of tests may be submitted for approval separately or in combination with the main collection of data.
The principal web-based survey and teacher web-based survey items have been previously piloted. Items were taken from the following sources: SRI: Integrated Studies of Educational Technology Teacher Survey, Spring 2001; U.S. Department of Education, National Educational Technology Trends Study: Teacher Survey, OMB No. 1875-0233; and the Empirical Education Item Bank. Some items may be slightly modified to reflect context and/or name of curriculum, or to reflect appropriate time span and/or frequency.
The Professional Development trainer checklist was developed based on various materials available from the trainers and AMSTI officials. These materials include: teachers’ guides in the relevant subjects, books and other materials on the training reading list, and PD training agendas. The Professional Development trainer checklist and Professional Development Participant Survey were piloted with all grade 5 and grade 7 math and science trainers in the 2006 training institutes.
The AMSTI Study Teacher Classroom Observation protocol was adapted from a synthesis of the Authentic Instructional Practices Classroom Observation form (Borman, Rachuba, Datnow, Alberg, Stringfield, & Ross, 2000), and the Reformed Teaching Observation Protocol (MacIsaac, Sawad, Daiyo, & Falconer, 2001). The observation and interview protocols will be piloted with at least four teachers: two science, two math, and with two raters for each pilot observation to assess inter-rater reliability.
Provide the name and telephone number of individuals consulted on statistical aspects of the design and the name of the agency unit, contractor(s), grantee(s), or other person(s) who will actually collect and/or analyze the information for the agency.
REL-SE Project Director: Ludwig D. van Broekhuizen (336) 315-7402
Study Manager: Jean Scott, SERVE Center (334) 242-9746
Senior Advisor: Robert Floden, Michigan State University (517) 355-3486
Task 2 Methodological Leader: Stephen Bell, Abt Associates (301) 634-1700
Co-PI: Denis Newman, Empirical Education Inc. (650) 328-1734
Co-PI: Richard Sawyer, Academy for Educational Development (202) 884-8868
1 In the original proposal we assumed that 81% of the variance in the outcome would be explained through the prior score covariate. The initial reviewers suggested that this was too high, we therefore lowered the value to .64. The first reviewers also asked us to make a judgment about the potential gains resulting from using a matched-pairs design. In our response we surmised that matching would account for 50% of the remaining variance (i.e., after conditioning the outcome on the pretest.) We showed that this would result in a drop in the MDES from .20 to .15. We have been advised that this expected benefit is too optimistic. We therefore assume a more conservative estimate of the potential benefit of matching, and conclude that, at worst, matching will not cause an increase in the MDES from the .20 level.
![]()
| File Type | application/msword |
| File Title | A Justification |
| Author | Lori Sterling |
| Last Modified By | Sheila.Carey |
| File Modified | 2007-05-10 |
| File Created | 2007-05-10 |
© 2026 OMB.report | Privacy Policy