Part B
PART B.docx
Consolidated Omnibus Budget Reconciliation Act Health Benefits Subsidy Under the American Recovery and Reinvestment Act of 2009 Evaluation
OMB: 1291-0001
Contents Mathematica Policy Research
CONTENTS
PART B: COLLECTION OF INFORMATION INVOLVING STATISTICAL METHODS
1. Respondent Universe and Sampling
2. Analysis Methods and Degree of Accuracy
3. Methods to Maximize Response Rates and Data Reliability
4. Tests of Procedures and Methods
5. Individuals Consulted on Statistical Aspects of the Design
References
TABLES
B.1. Estimated Population Sizes
B.2. Selection Probabilities Based on the UCP-COBRA Size Measure
B.3. Intended Final Numbers of Completed Interviews
B.4. Minimum Detectable Impacts on COBRA Take-Up Rates
B.5. Minimum Detectable Differences Between Study Populations During the ARRA Period in Rates of Any Health Insurance Coverage
Appendix A: Memorandum on the TAA Experiment
Appendix B: Reminder Mailings
PART B: COLLECTION OF INFORMATION INVOLVING STATISTICAL METHODS
The U.S. Department of Labor (DOL) contracted with Mathematica Policy Research to conduct an evaluation of the impact of a subsidy for health benefits under the Consolidated Omnibus Budget Reconciliation Act (COBRA) that was provided by the American Recovery and Reinvestment Act (ARRA) of 2009. The subsidy was available to workers who experienced involuntary termination of a job from September 2008 to May 2010, were eligible for COBRA at the time of job loss, and were not eligible for certain other health insurance options. The overall aim of the Mathematica evaluation is to determine whether and how people who had employer-sponsored health insurance maintained health care coverage after employment termination and whether the COBRA subsidy provided by ARRA led to increased health care coverage. DOL is requesting Office of Management and Budget (OMB) clearance for approval to conduct a one-time survey of randomly selected unemployment insurance (UI) recipients (COBRA Subsidy Study Survey) as part of this evaluation.
The study will provide a context for understanding the possible impacts of the ARRA subsidy by documenting characteristics of people who lost a job and became COBRA-eligible, separately by subsidy eligibility status. This descriptive and multivariate analysis will identify factors associated with COBRA enrollment after job loss and the impediments people might face in maintaining health care coverage for themselves and their dependents when employer-sponsored coverage is no longer available. The study will perform an impact analysis to determine how the availability of the ARRA subsidy changed COBRA utilization. The impact analysis will be addressed by comparing outcomes for a sample of subsidy-eligible individuals to a sample of otherwise similar individuals who were not subsidy-eligible. People in the latter group, called the subsidy comparison group, resemble subsidy-eligibles because they experienced involuntary job termination and were not eligible for another group health insurance plan, but their date of job loss did not occur during the qualification period. The analysis will adjust for differences between the groups that may be related to economic conditions or other factors.
1. Respondent Universe and Sampling
A goal of the evaluation is to be able to generalize the findings to several important populations. The sampling and analytic methodology will enable estimates of mean characteristics of the population of COBRA-eligible UI recipients, as well as estimates of the impact of the subsidy for the population of subsidy-eligible UI recipients. This section discusses the target populations and sampling methodology.
The target population of interest to the study consists of individuals who experienced an involuntary termination of employment during the subsidy qualification period or shortly after, and who were eligible for COBRA health insurance through their employer at that time. The sample population, which is expected to cover the majority of the target population, will consist of UI recipients who lost their jobs during that same period. In particular, the sample to be surveyed will consist of randomly selected subsidy eligible individuals who lost their jobs between February 17, 2009 and May 31, 2010, which includes most of the period in which a job loss could potentially enable workers to qualify for the subsidy.1 The study will also include a comparison sample, which will consist of workers who lost their jobs during the period following the end of the subsidy qualification, between June 2010 and March 2011. This comparison sample will largely consist of individuals who would otherwise have qualified for the subsidy, but were not eligible because of the timing of their job loss. This sample, weighted to resemble the characteristics of the subsidy-eligible sample at the time of job loss, will serve as a counterfactual, enabling the study to identify the impacts of the subsidy.2
The sample frame will be based on UI administrative records in the time periods of interest from a probability sample of 20 states. Within the selected states, a probability sample of UI recipients will be contacted and administered a screener that will determine whether they belong to any of the populations of interest to the study. A sufficient number of UI recipients will be screened so that the final sample contains completed interviews of 2,200 subsidy-eligible persons, 2,200 persons who were not eligible for the subsidy due only to the timing of their job loss, and 1,400 persons who were ineligible for the subsidy for reasons other than the timing of job loss. These sample sizes are chosen so that a five percentage point impact of subsidy availability on COBRA take-up rates—an impact regarded by DOL as substantively meaningful—is within the range of impacts detectable by this study.
The study’s sampling approach is designed to yield, in a cost-effective manner, a national probability sample from the study populations and periods in the UI sample frame. This approach will enable estimation of characteristics and impacts of the subsidy for the populations described in the previous section. Study estimates and measures of their precision will be design-based—that is, based explicitly on the sampling design. As such, the study estimates will be used to make inferences only on the sampled populations and time periods, which is appropriate because the subsidy was implemented only within the context of the particular economic conditions experienced in these populations and time periods.
a. Target Populations
The study sample will represent three target groups within the population of persons who lost their jobs involuntarily and became both unemployed and COBRA-eligible:
Subsidy-eligible. People who met all the requirements for being eligible for the subsidy, including having lost their jobs during the subsidy’s qualification period
Subsidy-comparison. People who were ineligible for the subsidy because their job separation occurred outside the subsidy’s qualification period, but who met all other requirements for subsidy eligibility
Subsidy-ineligible. People who were ineligible for the subsidy for a reason other than the timing of job separation, such as having access to insurance through a spouse or parent’s plan, or having access to other public health insurance
The first two groups are the key populations on which the study aims to measure the impact of subsidy availability. All three groups are relevant to addressing research questions on the broader population of COBRA-eligible job losers, including analyses of subsidy eligibility rates, characteristics of those who are eligible and ineligible for the subsidy, and determinants of COBRA take-up.
Within the three target populations, the study will require samples of people who lost their jobs in one of two periods: (1) the ARRA period, from February 17, 2009, to May 31, 2010, when job losers could qualify for the subsidy, as discussed above; and (2) the post-ARRA period, from June 1, 2010, to March 31, 2011, consisting of dates after the ARRA period and representing a time in which job terminations did not qualify anyone for the subsidy, which will be used to identify comparison group members. By definition, all sample members from the subsidy-eligible and subsidy-comparison populations will have lost their jobs in the ARRA and post-ARRA periods, respectively; the third target population, the subsidy-ineligible group, will be represented by sample members who lost jobs in either of the two periods.
b. Estimated Population Sizes
Table B.1 shows the estimated size of each target population. The number of job losers in the ARRA period is estimated by adding the number of UI first payments across all months in the ARRA period and all 50 states and the District of Columbia.3 A similar method is used for the post-ARRA period, but later months are assumed to have the same average number of first payments as earlier months since complete data for this period are not available as of the submission of this package. The estimated size of each subpopulation is calculated by multiplying the estimate of the total number of UI first payments and an estimate of the percentage of job losers who are COBRA-eligible and subsidy-eligible, described in more detail in the next subsection.
Table B.1. Estimated Population Sizes
|
Estimated Size of Population |
||
Target Population |
ARRA Period |
Post-ARRA Period |
Total |
Subsidy-eligible |
4,229,000 |
- |
4,229,000 |
Subsidy-comparison |
- |
2,091,000 |
2,091,000 |
Subsidy-ineligible |
1,812,000 |
896,000 |
2,708,000 |
Total COBRA-eligible |
6,041,000 |
2,987,000 |
9,028,000 |
All job losers |
15,897,000 |
7,860,000 |
23,757,000 |
c. Sample Frame
The ideal sample to answer the research questions would be a national probability sample of COBRA-eligible people spanning a range of prior employment experiences, routes to job separation, income levels, and levels of access to various sources of health insurance. However, there is no single, comprehensive frame of COBRA-eligible individuals, through either administrative records or existing surveys.
Instead, this study will use a sample frame of UI recipients, derived from UI administrative data obtained from states and henceforth called the UI sample frame. The study populations—that is, the specific populations to which the study findings can pertain—will consist of UI recipients within the three target populations (subsidy-eligible, subsidy-comparison, and subsidy-ineligible) rather than the entire target populations. Nevertheless, the UI sample frame is expected to include most of the people relevant to the study’s research questions. In addition, as discussed below, using the UI recipient data as a sample frame reduces substantially overall burden on respondents relative to a random sample of the population.
Each of the target populations consists of COBRA-eligible individuals who lose their jobs involuntarily and become unemployed, and the vast majority of these individuals are expected to be UI recipients. This is due to two key factors. First, the vast majority of unemployed, COBRA-eligible job losers are likely to be eligible for UI. More explicitly, the main conditions for a job separator to be UI-eligible are that (1) the job separation generally must have been involuntary (with some exceptions); and (2) the person’s earnings in a 12-month base period must exceed a minimal threshold, which typically ranges from $1,000 to $3,000 across states (Employment and Training Administration 2010). All persons in the target populations will achieve the first condition by definition; moreover, very few job losers whose earnings are too low to meet the second condition would likely have had employer-sponsored health insurance while employed.4 Second, among UI-eligible persons, a high proportion—more than 80 percent—actually file UI claims (Ebenstein and Stange 2010). The combination of these two factors implies that most unemployed, COBRA-eligible job losers are likely to appear in the UI administrative records.
Further limiting the sample frame to UI recipients, rather than all UI claimants, is expected to reduce burden on screener respondents without missing many members of the target populations. This is because most UI claimants who never receive UI payments fail to meet one of the two conditions for UI eligibility—that of involuntary job separation or having sufficient base-period earnings (Rangarajan et al. 2002) —and are thus also unlikely to be in the target populations. Other UI claimants who meet the two preceding conditions but do not collect a UI payment are likely to have become reemployed quickly, and are thus not of central interest to this study. Therefore, to reduce unnecessary expenditure of survey resources on screening individuals who are not of interest to the study, the study will focus attention on sampling UI claimants who received UI payments.
The UI sample frame can facilitate cost-effective and accurate data collection in a number of ways. First, in samples of UI recipients, the fraction of people belonging to the target populations is expected to be much higher than in samples drawn from the general population through, for instance, random digit dialing (RDD). RDD would induce a large burden on respondents, as it requires screening large numbers of people to find members of the study populations. For instance, from existing evidence, 24 to 29 percent of UI recipients from the ARRA period are subsidy-eligible,5 whereas less than 2 percent of all U.S. households contain subsidy-eligible persons.6 Thus, to achieve the sample size targets for the study populations, relying on the UI sample frame requires much less screening and creates far less burden on respondents than using RDD.
In addition, information in the UI records can improve both survey response rates and accuracy of the information collected from respondents. Contact information in these records will enable Mathematica to reach sample members by mail and by phone. Also, the records will have information on the name of the employer from which each worker separated prior to the filing of the UI claim, as well as the date of this separation; the interviewer can use this information to provide an anchor for the interview—that is, to direct the respondent’s attention to the precise job loss event on which interview questions are focused—and to aid the respondent’s recollection.
d. State Selection
A national probability sample of states will be drawn such that the final sample will consist of approximately 20 of the 51 UI jurisdictions, from which a complete listing of UI claimants during the specified time periods will be obtained. States with a larger number of UI claimants are likely to have more members of the target population and will be selected with greater probability. Specifically, states will be selected with probability proportional to a composite size measure that includes the size of the state’s UI recipient population in the ARRA period. This permits sample sizes to be similar across the selected states while minimizing variation in selection probabilities among individuals within the same study population. The sample of UI recipients from the post-ARRA period will, by design, represent the distributions of characteristics observed from the ARRA period; therefore, population sizes from the post-ARRA period do not need to be included in the measure of state size. For the state sample to represent a wide range of geographic regions, the state selection will be stratified by region, among other variables (see below).
The number of states to be sampled for the study has been determined by two factors. First, although collecting data from all 51 UI jurisdictions would improve precision by avoiding a clustered sampling design, the intensive recruitment efforts and cost-recovery payments required to do so would be prohibitively expensive, given the available resources. Second, the fixed sampling budget for the project implies a tradeoff between the gain in precision from increasing the number of states and the loss in precision from a smaller individual-level sample size. Based on the past experience of DOL and Mathematica in conducting similar large-scale surveys, sampling 20 states is anticipated to maximize overall precision: the precision gained by including additional states is expected to be outweighed by the precision lost due to the smaller sample size.
To reduce costs further and minimize the administrative data required, DOL will perform a single selection of states for this study and another study, the Evaluation of the Unemployment Compensation Provisions of the ARRA, referred to here as the UCP Evaluation.7 Both studies will rely on UI administrative records from the selected states as the basis for a sampling frame. Thus, each state’s composite size measure will also include components of importance to the UCP Evaluation. Although the populations of interest are not completely identical between the two studies, state selection probabilities identified by the two studies are very similar to the extent that study population sizes are highly correlated across states.
The composite size measure combines estimated statewide population sizes for all populations of interest to either study (Folsom et al. 1987). In particular, it is based on the following population size estimates:
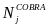 : the
estimated number of UI recipients in jurisdiction j whose job
termination occurred in the ARRA period, as measured by the number
of first payments during that period.
: the
estimated number of UI recipients in jurisdiction j whose job
termination occurred in the ARRA period, as measured by the number
of first payments during that period.
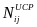 : the
number of UI first payments made in jurisdiction j during
period i. i indexes the four six-month periods
between October 1, 2007, and September 30, 2009.
: the
number of UI first payments made in jurisdiction j during
period i. i indexes the four six-month periods
between October 1, 2007, and September 30, 2009.
The first study population above is the focus of the COBRA Subsidy Evaluation, and the latter study populations are the focus of the UCP Evaluation. State-level, publicly available aggregate data on the number of first UI payments are used to form estimates of these population sizes.
To combine these
five statewide population counts into a single composite size
measure, each count is scaled by the national sampling rate for the
specified study population. For each study population, the national
sampling rate can be approximated by dividing the anticipated number
of people to be sampled from that group by the estimated statewide
population count. The national sampling rates for the five study
populations are denoted by
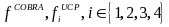 .
.
Given the national sampling rates and the estimated statewide population counts, the composite size measure for state j is
(1) 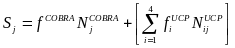 .
.
It is therefore a weighted sum of the five statewide population
counts, with weights equal to the national sampling rates for each
study population. Hence, using the joint size measure puts more
weight on jurisdictions with a greater number of individuals who lost
their jobs in the years before the subsidy qualification period than
if the measure were constructed for COBRA alone. However, the added
UCP component of the joint size measure is highly correlated with the
COBRA-alone size measure (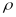 =
0.991), so adopting the joint measure will have little effect on the
jurisdiction-level selection probabilities.
=
0.991), so adopting the joint measure will have little effect on the
jurisdiction-level selection probabilities.
Among the 20 UI jurisdictions to be selected for the study, a few jurisdictions with the largest numbers of UI recipients, as gauged by their composite size measures, will be selected with certainty. These jurisdictions would appear in every random sample that could be drawn and would, on average, be included at least once if the sample were drawn with replacement. The remaining jurisdictions, known as noncertainty jurisdictions, will be selected without replacement using a sequential selection probability proportional to size (PPS) procedure (Chromy 1979) and using the stratification system described in more detail below.
Primary strata for selecting UI jurisdictions in the first stage of the sampling process will be formed to address analytic goals of the UCP and COBRA evaluations. The UCP evaluation must ensure that the sample includes adequate variability the maximum number of weeks of benefits (MNW) that became available through regular UI, the Emergency Unemployment Compensation Act of 2008, or the Extended Benefits program. Both evaluations must address potential bias in the survey estimates due to jurisdiction-level nonresponse.8 While the potential bias due to jurisdiction-level nonresponse is likely to be of greater concern for the UCP evaluation, the proposed stratification is not expected to have any adverse effect on the COBRA evaluation.
To achieve the first requirement of the UCP study, the first-stage selection will also be stratified according to the MNW in each jurisdiction. Three strata will be defined: (1) 60-79 weeks (12 states; “low”), (2) 86-94 weeks (8 states; “medium”), and (3) 99 or more weeks (30 states and DC; “high”).
Although the evaluation team will follow established practices to maximize response rates at every level (see section 3), UI jurisdictions may not cooperate with this study’s request for administrative claims data. Based on the experiences of Mathematica staff in conducting a 1990s study of the emergency unemployment compensation (EUC) program (Corson et al. 1999), UI jurisdictions that are experiencing more strain on their unemployment compensation system due to a worse economy may be less likely to cooperate. This could result in biased survey estimates if differences among states in economic conditions also affect the individual-level outcomes relevant to the COBRA study. To address this potential for nonresponse bias from jurisdictional-level nonresponse in both studies, first-stage selection will also be stratified according to the observed increase in the percentage change in UI first claims between calendar year 2007, a period that included the last business cycle peak, to calendar year 2009, a period that covered the trough of the recent recession. This stratification factor was chosen because the percentage change in claims (PCC) can be regarded as a proxy for the recessionary strain on the UC system within a state.9 Two strata will be formed based on the PCC variable: a “low” stratum containing jurisdictions in which the change in claims ranged from 23 to 74 percent (25 states and DC), and a “high” stratum in which the PCC variable ranged from 82 to 162 (25 states).10
Stratifying on the PCC variable will enable the creation of a randomly-selected reserve sample of UI jurisdictions that has a similar distribution of this measure of recessionary strains as the main sample. In the event that a jurisdiction refuses to provide data after intensive recruitment efforts, an additional randomly-selected jurisdiction from the same primary stratum (defined by the PCC and MNW variables together, as described below) can be released into the sample. Because the random addition to the sample will have a similar range for the PCC variable, augmenting the sample in this manner should reduce the likelihood that sample estimates are biased by differential nonresponse among states that experienced a certain extent of change in the volume of UI claims.
Sampling Rates by Primary Stratum. Crossing the two dimensions of stratification, the 5 primary jurisdiction-level sampling strata are:
Low PCC and low or medium MNW
Low PCC and high MNW
High PCC and low MNW
High PCC and medium MNW
High PCC and high MNW
It was necessary to collapse the low- and medium-MNW categories together within the low-PCC stratum because, otherwise, they would only contain four and two jurisdictions, respectively. Even after collapsing the two strata together, the expected number of selections from the resulting primary stratum is very small. As shown in the fourth column of Table B.2, a proportional allocation would have resulted in 0.88 states being drawn, on average, from primary stratum 1 over repeated sampling.
Table B.2. Selection Probabilities Based on the UCP-COBRA Size Measure
Primary Stratum |
Category for PCC Variable |
Category for MNW Variable |
Proportional Sampling |
|
Oversampling Low- and Medium-MNW Strata |
||
Expected Number of Jurisdictions in Sample |
|
Number of Certainty Selections |
Number of Random Selections in Main Sample |
Number of Jurisdictions in Reserve Sample |
|||
1 |
Low |
Low-Medium |
0.88 |
|
2 |
1 |
3 |
2 |
Low |
High |
11.37 |
|
3 |
4 |
13 |
3 |
High |
Low |
1.14 |
|
0 |
2 |
6 |
4 |
High |
Medium |
1.94 |
|
2 |
2 |
2 |
5 |
High |
High |
4.68 |
|
2 |
2 |
7 |
Sources: Values for the maximum number of weeks (MNW) variable were calculated using (1) annual UI policy information from the Comparison of State Unemployment Laws series archived by the U.S. Department of Labor, Employment and Training Administration (ETA) http://www.workforcesecurity.doleta.gov/unemploy/pdf/uilawcompar/ (accessed on 4/12/2011), and (2) weekly trigger notice data for the Extended Benefits and Emergency Unemployment Compensation Act of 2008 programs archived online at http://www.ows.doleta.gov/unemploy/claims_arch.asp (accessed on 4/12/2011). Values of the percentage change in claims (PCC) variable and the size measures used to calculate selection probabilities were constructed based on data on UI first payments and first claims available from ETA online at http://workforcesecurity.doleta.gov/unemploy/finance.asp (accessed 01/14/2011).
Notes: The figures in the table are based on the assumptions that 20 UI jurisdictions will be selected in the first stage of sampling and in the second stage: (1) 12,000 recipients with first payment dates between February 17, 2009, and May 31, 2010, will be selected for the COBRA subsidy evaluation (described further in section 3) and (2) 3,000 recipients with benefit year begin dates distributed equally across the four six-month intervals between October 1, 2007, and September 30, 2009, will be selected for the UCP study. Categories for the MNW and PCC variables were defined as described in the text. The expected number of selections with proportional sampling and the number of certainty selections with oversampling of the low- and medium-MNW stratum were calculated using the composite size measure displayed in equation (1).
Given the distribution of the size measure across the five primary strata, it was desirable to oversample in primary strata covering the low- and medium-MNW categories. Taking the oversampling rates into account, the fifth column Table B.2 shows the number of certainty selections in each primary stratum. These nine jurisdictions all would have expected selection frequencies larger than one using the revised sampling rates. The sixth column of the table shows the number of random selections in the main sample for in each stratum. This is equivalent to the number of randomly-selected jurisdictions included in the final sample if there were a 100 percent response rate. The final column of the table displays the number of additional UI jurisdictions in the reserve sample by stratum, which represents the maximum number of additional states that could be released into each stratum in the event of nonresponse in the initial sample.
With this specified design, selection probabilities for noncertainty states are as follows. If m noncertainty states are to be selected from a specified explicit stratum, then the probability that noncertainty state j is selected is
(2) ![]() ,
,
where
![]() is the size measure defined in Equation (1), and the denominator
represents the total combined size of all noncertainty states in the
specified explicit stratum.
is the size measure defined in Equation (1), and the denominator
represents the total combined size of all noncertainty states in the
specified explicit stratum.
e. Drawing Samples of Individuals in the Selected States
The administrative UI records from each selected state will form the basis of a sample frame from which people will be selected to be screened for the survey. Initial UI claims resulting in a payment represent the final sampling units within each state. Because subsidy eligibility depends on whether a person’s date of job separation occurs in the ARRA period, UI claims will be classified into the ARRA and post-ARRA periods according to the dates of job separation.
Within each study population, the sample from the ARRA period will have equal probabilities of selection; that is, sample members will have nearly equal weights. This will provide for greater precision in both the descriptive analyses of the subsidy-eligible population and the impact analyses. The sample from the post-ARRA period will be drawn to have a similar allocation across states as that from the ARRA period. This enhances the internal validity of the impact analyses by rendering the subsidy-eligible and subsidy-comparison samples more similar.
Because not all UI recipients are COBRA-eligible, the study will draw a larger initial sample to participate in screening. The brief screener will collect information needed to determine whether a UI recipient is eligible for the survey, and if so, to which of the three study groups he or she belongs. The initial sample will be sufficiently large to produce the desired final sample in each group, described in more detail in the next section.
The allocation of the initial sample is determined in the following manner. For the ARRA period, the number of initial sample members selected from state j, denoted by njCOBRA is
(3) 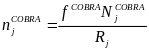
where NjCOBRA is
the number of UI recipients in the ARRA period in state j;
![]() is the probability of selecting state j (see the previous
subsection); and
is the probability of selecting state j (see the previous
subsection); and
![]() is the national sampling rate in the ARRA period, which is a constant
chosen so that the entire initial sample (from all selected states)
yields a final sample that meets the sample size targets for the ARRA
period. This allocation seeks to equalize the probability of
selection for UI recipients into the initial sample. Moreover,
because all initial sample members from a specified study population
will have an equal probability of being screened into the final
sample, the final sample from the ARRA period will have nearly equal
weights within each study population. The initial sample from
the post-ARRA period will be allocated across states in similar
proportions as the initial sample from the ARRA period. The
allocation will be designed to have similar distributions across
states for the final subsidy-eligible and subsidy-comparison samples.
is the national sampling rate in the ARRA period, which is a constant
chosen so that the entire initial sample (from all selected states)
yields a final sample that meets the sample size targets for the ARRA
period. This allocation seeks to equalize the probability of
selection for UI recipients into the initial sample. Moreover,
because all initial sample members from a specified study population
will have an equal probability of being screened into the final
sample, the final sample from the ARRA period will have nearly equal
weights within each study population. The initial sample from
the post-ARRA period will be allocated across states in similar
proportions as the initial sample from the ARRA period. The
allocation will be designed to have similar distributions across
states for the final subsidy-eligible and subsidy-comparison samples.
The initial sample of individuals whose job was terminated in the post-ARRA period will be constructed in a manner such that the samples from the ARRA and post-ARRA periods will have similar observable characteristics. This will be done by oversampling post-ARRA individuals whose observable characteristics are underrepresented in the post-ARRA period relative to the ARRA period. The characteristics to be balanced between the ARRA and post-ARRA samples are those that are recorded in the administrative UI data: gender, race, age, base-period earnings, and local unemployment rates.
Propensity score weighting methods will be used to select the sample, and the following propensity score model will be estimated as a logit regression.11 Letting Ai indicate that the job separation for individual i occurred in the ARRA period,
(4) 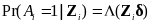
where Zi is a vector of the characteristics
discussed earlier and
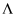 is
the logit function. From the regression estimates, every UI
recipient’s estimated propensity score,
is
the logit function. From the regression estimates, every UI
recipient’s estimated propensity score,
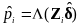 , will
be estimated. The propensity score represents the predicted
probability that the worker’s job separation occurred in the
ARRA period. Every individual will be classified into one of several
intervals of the estimated propensity score. The propensity score
intervals will essentially partition the state’s UI recipient
population into strata, referred to as propensity score strata.
Following standard practice, a sufficient number of strata will be
created so that mean propensity scores are similar between ARRA and
post-ARRA individuals in the same stratum (Rosenbaum and Rubin 1983;
Dehejia and Wahba 1999; Imbens 2004).
, will
be estimated. The propensity score represents the predicted
probability that the worker’s job separation occurred in the
ARRA period. Every individual will be classified into one of several
intervals of the estimated propensity score. The propensity score
intervals will essentially partition the state’s UI recipient
population into strata, referred to as propensity score strata.
Following standard practice, a sufficient number of strata will be
created so that mean propensity scores are similar between ARRA and
post-ARRA individuals in the same stratum (Rosenbaum and Rubin 1983;
Dehejia and Wahba 1999; Imbens 2004).
After forming the propensity score strata, individuals will be selected within each state in the following manner. First, from the ARRA period, a random sample of individuals will be selected, with implicit stratification by the propensity score strata, date of job loss (year and quarter), and demographic information. Implicit stratification will enable the sample to have a similar distribution across strata and demographic groups as the full UI recipient population in the ARRA period; moreover, implicitly stratifying by the date of job loss will improve the spread of UI recipients who are selected across the ARRA period. Second, from the post-ARRA period, individuals will be selected such that the sample also has the same allocation across strata as the UI recipient population in the ARRA period. This procedure is expected to produce ARRA and post-ARRA initial samples that are balanced on the characteristics measured in the UI data.12
f. Response Rates
An overall response rate of 80 percent is estimated for the survey. Details are provided in section 3.
2. Analysis Methods and Degree of Accuracy
The analytic methods and selected sample sizes will enable the study to identify estimates of program impacts and the distribution of characteristics of the study populations with sufficient precision to address the research goals. This section discusses the sample sizes, degree of precision, analytic methods, and construction of weights.
a. Sample Sizes and Precision
For each category of individuals defined by target population and period of job loss, Table B.3 shows the intended number of completed interviews. The subsidy-eligible and subsidy-comparison groups, each of which will be represented by 2,200 completed interviews, will be allocated larger sample sizes because of their importance in the impact analyses. The intended sample of 1,400 subsidy-ineligible individuals (split evenly between the ARRA and post-ARRA periods) will permit descriptive analyses of a broader population of COBRA-eligible job losers.
Table B.3. Intended Final Numbers of Completed Interviews
|
Intended Final Number of Completed Interviews |
||
Target Population |
ARRA Period |
Post-ARRA Period |
Total |
Subsidy-eligible |
2,200 |
- |
2,200 |
Subsidy-comparison |
- |
2,200 |
2,200 |
Subsidy-ineligible |
700 |
700 |
1,400 |
Total |
2,900 |
2,900 |
5,800 |
Estimated number of UI recipients screened |
11,000-13,000 |
11,000-13,000 |
22,000-26,000 |
As indicated in the previous section, the study requires drawing a larger initial sample of UI recipients in order to yield the desired number of completed interviews in each group. An estimated 22,000 to 26,000 persons will be drawn for the initial sample to produce the final sample of 5,800 respondents. This estimate assumes an overall response rate of 80 percent and 21 to 25 percent of respondents who screen in as subsidy-eligible or subsidy-comparison.13 The subsidy-ineligible sample will be identified through the same screening process.
The intended sample sizes for this study will enable the detection of impacts of 5 percentage points in a variety of scenarios. Table B.4 shows the Minimum Detectable Impacts (MDI) under various sample definitions and assumptions about COBRA take-up rates in the subsidy-comparison sample. In general, achievable levels of precision are higher when there is less underlying heterogeneity in outcomes. Dichotomous outcomes are most heterogeneous at a prevalence of 50 percent; thus, impacts on COBRA take-up rates can be detected more readily when take-up rates in the subsidy-comparison group are further from 50 percent. MDIs are shown under assumed take-up rates of 15 and 25 percent in the subsidy-comparison sample; this range includes the 19 percent take-up rate estimated by Hewitt Associates for the time period just before the subsidy became available (Bovbjerg et al. 2010).
Table B.4. Minimum Detectable Impacts on COBRA Take-Up Rates
|
Number
of |
Minimum Detectable Impact, in Percentage Points, if Take-Up Rate in Subsidy-Comparison Sample Is |
|
Analysis Sample |
15 Percent |
25 Percent |
|
All subsidy-eligible and subsidy-comparison individuals |
4,400 |
3.4 |
4.1 |
50 percent sub samples of the subsidy-eligible and subsidy-comparison samples |
2,200 |
4.3 |
5.2 |
Note: The calculations are based on the following assumptions: 80 percent level of power; a two-tailed test at a 5 percent significance level; 9 certainty states contain 42 percent of the sample14; 11 noncertainty states contain 58 percent of the sample; 3 percent of the total outcome variance is observed across states; the correlation between statewide mean outcomes of the subsidy-eligible and subsidy-comparison populations in the same state is 0.7; and covariates explain 20 percent of the variance in outcomes.
Using the full sample of 2,200 subsidy-eligible and 2,200 subsidy-comparison individuals, the study can detect impacts as low as 3.4 and 4.1 percentage points if take-up rates in the subsidy-comparison sample are 15 and 25 percent, respectively (Table B.4). In subsamples that make up half the full sample—for instance, in the bottom half of the sample income distribution—MDIs range from 4.3 to 5.2 percentage points. Thus, the expected levels of precision are sufficient for detecting policy-relevant impacts in both the full sample and important subgroups.
In addition to estimating impacts of subsidy availability, the study will also produce descriptive estimates of the characteristics and experiences of the study populations. As many of these descriptive estimates will measure the average difference in a specified variable between two study populations, the expected precision of these estimates is captured by the minimum detectable difference (MDD)—the smallest difference between groups that can be reliably detected.
Several of the group comparisons will assess average differences between subsidy-eligible (or subsidy-comparison) and subsidy-ineligible individuals. In general, MDDs for these comparisons are expected to be higher than the MDIs in the impact analyses because of smaller sample sizes from the subsidy-ineligible group. Table B.5 shows the MDD for one illustrative quantity of interest—the difference in rates of any health insurance coverage between subsidy-eligible and subsidy-ineligible individuals who lost their jobs in the ARRA period. The MDD ranges from 6.7 to 6.8 percentage points, depending on the prevailing rate of health insurance coverage. Thus, although the descriptive estimates will be less precise than the impact estimates, the study will likely be able to detect a large range of the differences that might reasonably be observed between study populations.
Table B.5. Minimum Detectable Differences Between Study Populations During the ARRA Period in Rates of Any Health Insurance Coverage
|
Number
of |
Minimum Detectable Difference, in Percentage Points, if Rate of Health Insurance Coverage Is |
|
Groups to Be Compared |
50 Percent |
60 Percent |
|
Subsidy-eligible (2,200) and subsidy-ineligible (700) individuals from the ARRA period |
2,900 |
6.8 |
6.7 |
Note: The calculations are based on the following assumptions: 9 certainty states contain 42 percent of the sample; 11 noncertainty states contain 58 percent of the sample; 3 percent of the total outcome variation is observed across states; and the correlation between statewide mean outcomes of any two subgroups of UI recipients in the same state is 0.7.
b. Econometric approach
The core of the econometric approach for the impact analysis is to measure differences in outcomes between subsidy-eligible and subsidy-comparison individuals who share the same observable characteristics. This approach assumes that subsidy-eligible individuals, on average, would have exhibited the outcomes of subsidy-comparison individuals with the same characteristics if the subsidy had not been available. As described in the previous section, the sampling methodology will select subsidy-eligible and subsidy-comparison samples with similar distributions of characteristics that are available in the UI administrative data. The method is designed to produce a subsidy-comparison group that has characteristics similar to those of the subsidy-eligible group and, as a result, to enable the analysis to produce an unbiased estimate of the impact of subsidy availability with a simple difference in the mean outcomes.
However, the subsidy-eligible and subsidy-comparison groups will not be identical in observable characteristics measured in the survey. Any differences will be controlled with the simultaneous use of two econometric methods: propensity score weighting and regression analysis. Propensity score weighting gives greater weight to subsidy-comparison individuals whose observable characteristics bear a stronger resemblance to those of subsidy-eligible individuals, while regression analysis models the association between observable characteristics and outcomes and directly adjusts outcome differences by netting out their influence. Conceptually, the impact of subsidy eligibility will be estimated by the difference between the average outcome of the subsidy-eligible sample and the reweighted, regression-adjusted average outcome of the subsidy-comparison sample.
The key advantage of this approach is that it provides multiple layers of safeguards against biases arising from background differences between the groups (Robins and Rotnitzky 1995). Through the use of both propensity score weighting and regression analysis, background differences that are not fully accounted for by one method will be addressed by the other. In particular, the regression analysis will adjust for the small background differences that might remain after the subsidy-comparison sample has been reweighted to mimic the characteristics of the subsidy-eligible sample, and the reweighting will reduce any bias due to the assumption implicit in the regression analysis that the effect of each characteristic is linear. These econometric adjustments are expected to be small in light of the sampling strategy and will adjust primarily for differences in characteristics captured by baseline information from the survey that is not available in the UI administrative data.
Analytic weights will be computed that account for the survey sampling methodology, including a nonresponse adjustment. Furthermore, people in the post-ARRA samples will be assigned greater weight to the extent that their characteristics more closely match those of the ARRA period. This weighting will be based on the propensity score, or the predicted probability that an individual lost a job in the ARRA period conditional on relevant characteristics. With these final weights specified, a regression analysis will be used to estimate the impacts of subsidy availability on various outcomes. Details of the construction of these weights are provided in the next subsection.
Estimation
procedure. The primary outcome is measured with a dichotomous
variable,
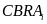 for whether individual i enrolls in COBRA at any time during
his or her period of COBRA eligibility. Accordingly, impacts on COBRA
take-up will be estimated with a logit regression,
for whether individual i enrolls in COBRA at any time during
his or her period of COBRA eligibility. Accordingly, impacts on COBRA
take-up will be estimated with a logit regression,
(5) 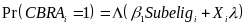 ,
,
that controls for a vector of covariates (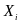 )
and weights sample members by their final weights. The coefficient of
interest,
)
and weights sample members by their final weights. The coefficient of
interest,
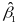 ,
will be transformed into an estimated impact on COBRA take-up
expressed in percentage points. Impacts on other dichotomous
outcomes, such as take-up of any health insurance, will be estimated
in a similar manner. For each continuous outcome
,
will be transformed into an estimated impact on COBRA take-up
expressed in percentage points. Impacts on other dichotomous
outcomes, such as take-up of any health insurance, will be estimated
in a similar manner. For each continuous outcome
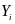 ,
impacts will be modeled with a linear regression,
,
impacts will be modeled with a linear regression,
(6) 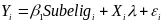 ,
,
estimated with weighted least squares on the basis of the final weights.
The vector of
covariates
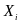 is included in equations (5) and (6) both to reduce bias and to
increase precision. The reweighting of subsidy-comparison group
members may leave small differences between the subsidy-eligible and
subsidy-comparison groups, and the regression adjustment will reduce
any bias caused by these remaining differences, which may be
correlated with take-up. To the extent that the covariates explain
variation in COBRA take-up within the subsidy-eligible or
subsidy-comparison groups, the precision of the impact estimate is
improved. Conversely, correlation between covariates and
subsidy-eligibility status may reduce precision, but this
effect is likely to be small, since the reweighting ensures similar
distributions of characteristics between subsidy-eligible and
subsidy-comparison groups.
is included in equations (5) and (6) both to reduce bias and to
increase precision. The reweighting of subsidy-comparison group
members may leave small differences between the subsidy-eligible and
subsidy-comparison groups, and the regression adjustment will reduce
any bias caused by these remaining differences, which may be
correlated with take-up. To the extent that the covariates explain
variation in COBRA take-up within the subsidy-eligible or
subsidy-comparison groups, the precision of the impact estimate is
improved. Conversely, correlation between covariates and
subsidy-eligibility status may reduce precision, but this
effect is likely to be small, since the reweighting ensures similar
distributions of characteristics between subsidy-eligible and
subsidy-comparison groups.
The vector of
covariates will include personal characteristics before or at the
time of job loss that are likely to be correlated with COBRA take-up
decisions or other outcomes. These outcomes may be linked to income,
occupation, health status, or utilization of medical care before job
loss, age, education, marital status, or number of dependents. Any
covariates that may be correlated with outcomes and differ between
the subsidy-eligible and subsidy-comparison groups will be included
in the vector both for the purposes of computing the regression
weights and for the regression adjustment. Outcomes that may be
affected by the subsidy’s availability or characteristics
measured after job loss are not included in
![]() .
.
The impact of the subsidy’s availability can be estimated separately for subgroups of interest, including low-income individuals or people who report being in poor health at the time of job loss. In addition, a similar framework will be used to test whether the impact is different for two or more subgroups by including in the regression the interaction between subsidy-eligible status and the subgroup indicator. The difference in the impact of the subsidy’s availability on COBRA take-up rates for low- and high-income individuals, for example, will be estimated using a logit regression,
(7) 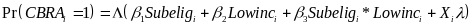
where Lowinci is equal to 1 if the person
had below-the-median income before job loss and 0 otherwise, and the
vector of covariates
![]() no longer contains Lowinci. A logit
regression with the same weights as used to estimate Equation (5)
will be used to estimate
no longer contains Lowinci. A logit
regression with the same weights as used to estimate Equation (5)
will be used to estimate
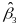 ,
which will be transformed into the difference in impacts between the
subgroups.
,
which will be transformed into the difference in impacts between the
subgroups.
Descriptive analyses. In addition to the impact analysis, data collected in the survey will be used to address the study’s other research questions. The characteristics of COBRA-eligible and subsidy-eligible individuals will be documented using means and frequencies. Means and frequencies will be computed for each of the subpopulations, separately by time period, and for the population of COBRA-eligible job losers as a whole. Comparisons will be drawn across subpopulations and over time by computing means and performing t-tests. In addition to the means and frequencies, descriptive logit analyses will be estimated to show correlates of the propensity to be subsidy-eligible and correlates of COBRA enrollment among COBRA-eligibles. As in the impact analysis, appropriate weights will be applied in these analyses to generate unbiased statements about each group and comparisons across the groups, despite the possibly unequal probability of sampling. Statistical tests comparing characteristics of different populations will also account for the complex survey design, using the variance estimation methods described below.
Variance Estimation for Descriptive Measures. Test of significance for point estimates and contrasts calculated in the descriptive analysis will be based on variance estimates that explicitly account for the complex survey design, for example, clustering, stratification, and weighting. These design-based variances will be estimated using Taylor linearization (see, Binder 1983 and Sections 5.5 through 5.10 of Särndal et al. 1992) as implemented in SUDAAN, SAS, or Stata. (In Särndal et al. [1992], equations 5.5.7 and 5.5.8 present the basic equations for the first-order Taylor series approximation; the application of the Taylor series approximation for variance estimation of ratios is given in Section 5.6, for means in Section 5.7, and for regression coefficients in Section 5.10.) A finite population correction will not be made at either the individual level or jurisdiction level so that the study will have some capacity to generalize inference based on the results beyond the study population.
Variance Estimation for Impact Estimates. As with the descriptive point estimates, variances for the estimated impact parameters can be estimated using Taylor linearization in SUDAAN, SAS, or Stata. (See the references provided previously on the use of the Taylor series approximation for variance estimation.) Such variance estimates will take into account variation in the impact parameters arising from the design of the survey.
c. Construction of Weights
Each of the analyses based on the survey data will use appropriate weights so that the estimates can be generalized to the appropriate population. These weights will be developed using a two-stage process: (1) computation of initial sampling weights; and (2) adjustment of the sampling weights for nonresponse. Each of these steps is discussed below.
Initial Sampling Weights. In the first step, initial sampling weights are computed based on the probability of selection at each of the two stages (UI jurisdictions and individuals within jurisdictions). In the first stage of the sample design, the certainty jurisdictions will have weight of 1 and the randomly selected (noncertainty) jurisdictions will have a sampling that is inversely proportional to the probability of selection. The second-stage weight component will be based on the probability of an individual being selected from the UI claims records. This component will vary within each of the strata described above.
Nonresponse Adjustments. In the second step, the sampling weights are adjusted for nonresponse at both stages. Nonresponse at the jurisdiction level will be handled differently based on whether the jurisdiction is selected with certainty or the jurisdiction is a non-certainty jurisdiction.
A certainty jurisdiction is, by definition, a jurisdiction with a sufficiently large population size that the jurisdiction is unique. Therefore, if a certainty jurisdiction refuses to provide UI administrative claims records for this evaluation, the study population will be redefined to exclude the persons in the noncooperating jurisdiction. Survey estimates will then enable inferences to the population of individuals in the remaining jurisdictions. The redefinition of the population for inferences is a conservative approach since it limits the inferences to a population that had a chance of inclusion into the study. If a noncertainty jurisdiction refuses to cooperate with a data request, this refusal will be accounted for in the nonresponse adjustment for the individual-level sampling weights.15
Individual-level nonresponse adjustments will be made using response propensity modeling and post-stratification. In essentially all surveys, the sampling weights need to be adjusted to account for sample members who cannot be located or who refuse to respond once located. The adjusted weight is the product of the sampling weight and an adjustment factor. The approach to be used in this study to calculate adjustment factors is a generalization of the commonly used method in which “weighting classes” of sample members with similar characteristics are formed and adjustment factors are calculated as the inverse of the weighted response rate in that class. This method produces unbiased estimates of population parameters when the (unobserved) outcomes and characteristics of individuals in the same weighting classes are the same, on average. The natural extension to the weighting class procedure is to use logistic regression with the weighting class definitions used as covariates. The logistic regression approach also has the ability to include both continuous and categorical variables, and standard statistical tests are available to evaluate the selection of variables for the model (Särndal et al. 1992).
For individual-level nonresponse, weights will be adjusted for three different types of nonresponse, depending on whether the UI recipient: (1) could not be located, (2) refused to complete a screener, or (3) qualified for surveying but refused to complete the survey. A weighted logistic regression will be used to model the propensity to be located or to respond. The propensity scores that are computed from the logistic regression models will be used to create the weighting classes, where weights of nonrespondents are reallocated to respondents. The adjusted weight for each sample case is the product of the initial sampling weight and the adjustment factors.
Each logistic nonresponse model will be fitted by first identifying a pool of covariates to work from using stepwise regression, then assessing candidate models using various measures of goodness of fit and predictive ability. The covariates will include factors or attributes that can be obtained from administrative data and (1) which are likely to be associated with differences in the likelihood that a sample member is located and interviewed and (2) are likely to be related to the outcomes of interest for this study. Specific examples include:
Pre-claim earnings, occupation, and industry
Reason for separation from pre-claim job
Age
Gender
Race and ethnicity
Geographic location
A chi-squared automatic interaction detector (CHAID) will be used to refine the list of candidate independent variables and identify interactions among them.16 The CHAID procedure iteratively segments a data set into mutually exclusive subgroups that share similar characteristics based on their effect on nominal or ordinal dependent variables. It automatically checks all variables in the data set and creates a hierarchy that shows all statistically significant subgroups. The algorithm finds splits in the population, which are as different as possible based on a chi-square statistic. It is a forward stepwise procedure, and it finds the most diverse subgrouping, and then each of these subgroups is further split into more diverse sub-subgroups. Sample size limitations are set to avoid generating cells with small counts. The algorithm stops when splits no longer are significant; that is, the group is homogeneous with respect to variables not yet used or when the cells contain too few cases. The CHAID procedure results in a tree that identifies the set of variables and interactions among the variables that have an association with the ability to locate a sample member and the propensity of a located sample member to be a respondent (eligible or ineligible).
The variables and interactions identified using CHAID then will be processed using forward and backward stepwise regression (using SAS Logistic procedure with weights normalized to the sample size) to further refine the candidate variables and interaction terms. After identifying a smaller pool of main effects and interactions for potential inclusion in the final model, a set of models will be evaluated to determine the final model. Because the SAS stepwise logistic procedures do not incorporate the sampling design, the final selection of the covariates will be accomplished using the logistic regression procedure in SUDAAN (Research Triangle Institute 2004).
Comparison Group Weights. To carry out the impact estimation, analytic weights for the subsidy-comparison group will be standardized to the distribution of the subsidy eligible population. Construction of these weights will use propensity score methods with individual and local area characteristics at the time of job loss measured in the survey and administrative data.
d. Use of Periodic Data Collection to Reduce Burden
The data collection instrument is designed to collect all required information in a single survey.
3. Methods to Maximize Response Rates and Data Reliability
a. Response Rates
As described in section 2.c, this study has two levels of potential nonresponse: the state and the selected individual UI recipients in a state. While the study aims to achieve 100 percent cooperation among the states, some states may refuse to provide the needed data. As with any survey, some nonresponse among the UI recipients selected for the study is inevitable. DOL and Mathematica will take steps to maximize response rates at both levels and to address potential bias through state and individual nonresponse analysis.
The study will maximize state participation by adopting practices employed in previous successful recruitment efforts. In the recent Impact Evaluation of the Trade Adjustment Assistance Program (TAA study), the contractors (Social Policy Research and Mathematica) requested that states deliver large, multipart UI administrative data files in 2010, after the end of the recession. UI claims and wage data were successfully obtained from all 26 states that were contacted for the TAA study. The COBRA study will adopt state recruitment methods used by the TAA study, including coordinating recruitment efforts between DOL and the contractor, simplifying the data request and offering logistical support, and offering cost-recovery payments.
The study will similarly seek to improve individual response rates by adopting successful practices. The methods employed will address all types of individual nonresponse, including failure to locate the individual or refusal to participate in the screener or the full survey.
The process of locating UI recipients selected for the study will begin before sending out the first mailing. This locating process will involve the use of an independent vendor that will check the full sample against current address databases. This first step is critical given that (1) the contact information for some sample members may be outdated and (2) some sample members may have moved. Extensive tracking and locating procedures that have proven successful in other Mathematica studies will be used for sample members whose mail is returned as undeliverable. These include using other independent databases, checking with neighbors and family members, and searching social networking sites. When talking with contacts, the specific purpose of the call will not be disclosed, but it will be stated that the effort to reach the sample member is for an important study being sponsored by the government.
Being faced with an increasing number of unsolicited calls, Americans are becoming more reluctant to participate in telephone surveys. Armed with the latest call screening technology, they are exercising more choice over when and how they can be contacted. Survey organizations that employ telephone surveys are finding that their response rates have been steadily decreasing in recent years. Curtin, Presser, and Singer (2005) found that the decline in telephone survey response rates from 1996 to 2003 was much steeper than in previous years. This decline corresponds with the proliferation of caller ID and other screening devices such as answering machines, voice mail, and call blocking. From 1995 to 2000, there was a 34.8 percent increase in American households that use Caller ID, and the majority of those households report using the technology to screen their calls “always” or “most of the time” (Tuckel and O’Neill 2001).
Mathematica will use a variety of procedural methods as well as offer respondents an incentive payment for completing the survey. Using its experience conducting surveys with unemployed individuals and other hard-to-reach populations, Mathematica will implement procedures that will maximize survey response and ensure the collection of reliable data for the COBRA Subsidy Study. The procedures that will be employed to achieve the targeted 80 percent response rate include the following:
An advance letter describing the purpose and sponsorship of the survey will be mailed to sample members at the address obtained from UI administrative records. This advance letter will be printed on DOL letterhead, but the envelope’s return address will be Mathematica’s to facilitate the processing of undeliverable mail and tracking. In an experiment conducted for the TAA study for DOL, Mathematica introduced the use of DOL letterhead for nonrespondents who had previously received a survey invitation letter on Mathematica letterhead, while keeping the incentive offer constant. The results of that experiment suggest that the switch to agency letterhead and envelope improved response rates among previous nonresponders. (See Appendix A for a memo detailing the experiment.)
The advance letter will explain that Mathematica is conducting interviews for a DOL-sponsored research study and not soliciting donations or selling anything. The letter will also explain that the data collected will be kept private. Toll-free numbers will be provided in the letter for sample members to call and complete initial screening and full interviews, if appropriate. Further, an information sheet containing typical questions asked by study participants and responses to those questions will be part of the advance mailing. Extensive tracking and locating procedures that have proven successful in other Mathematica studies will be used. Multiple methods for tracking and locating UI recipients will be used, including the use of extracts from state administrative data, the use of an independent vendor providing commercially available contact information, and Mathematica’s respondent tracking efforts to locate sample members.
Reminder mailings to nonrespondents to encourage response. These reminder mailings—a postcard and a final appeal letter—will stress the value of the sample member’s input to the research study and will also remind them of the potential earning opportunity. As with the advance letter, the reminder mailings will use the DOL logo and name, with a Mathematica address for the return address. Using the agency letterhead and logos are more likely to engage sample members and encourage response than will the Mathematica name. Drafts of these documents are included as Appendix B.
The use of a combination of CATI and the IVR system to maximize the ability to screen sample members. The IVR system is expected to increase response rates to the screening survey by appealing to a subset of sample members who prefer this option and may not respond to interviewer-initiated contact attempts, i.e. those using caller ID to screen calls. The IVR provides sample members the option of calling in at their convenience. It is also helpful in connecting with sample members for whom the telephone contact information obtained from the UI administrative records is invalid, since some of these sample members will call in on their own. Using CATI ensures control of sample releases, convenient call scheduling, and questionnaire logic and completeness.
Interviewer training that stresses the importance of respondent cooperation and develops skills for averting and converting refusals.
A short and simple screening interview, estimated to take about two minutes to complete.
The ability to conduct the interview in Spanish as well as English.
In addition to the procedures outlined above to maximize response and data reliability, an incentive payment of $50 for completing the full survey will be offered to those respondents who screen in through the IVR system and complete the full interview within four weeks. Forty dollars will be offered to those who complete the full survey after being screened in by a Mathematica interviewer and to IVR completers who complete the full survey outside of the four week window. The use of incentives has become more widespread as surveys try to address the problem of declining response to telephone surveys. Curtin, et al. 2005 note that the rise in effort and costs associated with achieving high response rates has made the use of incentives a more common practice. Jäckle and Lynn (2007) further acknowledge that respondent incentives are increasingly used as a measure of combating falling response rates and resulting risks of nonresponse bias.
Using these procedures, an estimated overall response rate of 80 percent will be achieved; 83 percent of sample members are expected to respond to the screening interview, and of those who complete and pass the study screens, 96 percent are expected to complete the full interview (0.83*0.96=0.80).
b. Reliability of Data Collection
Several methods will be implemented to ensure that the data collected are reliable. First, to make sure that sample members are clear about the separation of interest to the study, the job separation date and employer name will be included in the advance mailing they receive. Respondents will be reminded of this information when they call in either to the IVR or to Mathematica. All respondents to the screener will be asked exactly the same questions, regardless of the mode selected.
Another approach that will ensure the reliability of the data collected is the survey’s reliance on widely used questions that have been tested in the field. The draft questionnaire for the COBRA Subsidy Study draws heavily from questionnaires developed for other DOL studies, including the Trade Adjustment Assistance Study Follow-Up Survey (OMB number 1205-0460) and the Individual Training Account 2 (ITA2) Follow-up Questionnaire (OMB 1205-0441); as well as surveys conducted for other agencies such as the Accelerated Benefits Demonstration Project (OMB 0960-0747) conducted for the Social Security Administration. The questions in the COBRA Subsidy Study Survey were designed to be easily understood by respondents and interviewers and were refined based on internal reviews at Mathematica, reviews by staff at DOL, and comprehensive pretesting.
Other recall aids such as dates of employment subsequent to job loss and dates of participation in other health insurance plans, will be recorded and retained by the CATI program for easy reference and use at appropriate questions. Use of CATI to conduct the survey also helps ensure the reliability of the data by controlling question branching (reducing item nonresponse due to interviewer error), modifying wording (providing memory aids and probes and personalizing questions), and constructing complex sequences that are not possible to produce or are less accurate in hard-copy surveys. The probes, verifications, and consistency checks are built into the system’s standardized procedures. These procedures ensure the reliability of the data collection methods and the data collected through those methods.
Supervisory staff at Mathematica’s Survey Operation Center (SOC) will monitor at least 10 percent of each interviewer’s work using silent call-monitoring equipment and video monitors that display the interviewer’s screen. Supervisors evaluate interviewer performance based in part on this monitoring. Supervisors then discuss these evaluations and coach interviewers to ensure high-quality data collection. Retraining and/or re-assignments are provided as needed.
c. Nonresponse Bias Analysis
A bias may arise in study results if participating jurisdictions and individuals differ from the target population as a whole. The nonresponse bias analysis will provide some indication of whether a possible nonresponse bias exists and the data items and populations for which survey estimates might have a greater potential for bias. However, because survey data will not be available for nonrespondents, the analysis can never determine conclusively if bias does or does not exist in the survey estimates.
Nonresponse Bias Analysis at the Jurisdiction Level. Jurisdiction-level nonresponse results in the exclusion of a relatively large number of people, and the reason for the refusal of the jurisdiction to provide data may be correlated with the outcomes of interest for this evaluation. To assess the possibility of bias arising from jurisdiction-level nonresponse, both qualitative and quantitative analyses will be conducted.
The qualitative analysis will concentrate on the reasons for refusal given by UI jurisdictions that choose not to cooperate with the data request. Of particular concern is whether economic conditions or policies that could affect the outcomes of interest for this evaluation play a role in a refusal to provide data because this may indicate a potential for bias. The results of the qualitative analysis could be consistent with the expectation that UI jurisdictions experiencing more strain on their unemployment compensation system due to the recession are less likely to cooperate with a data request. In that case, the first-stage stratification system described in section 1 would be expected to mitigate the potential bias arising from differences across jurisdictions in the increase in UI claims stemming from recessionary strains. Depending on the results of the quantitative analysis described below, this could increase the confidence with which the study team might be able to make robust inference about the national population of COBRA-eligible UI recipients using the sample of jurisdictions selected for this study. Alternatively, if UI jurisdictions identify other economic factors or policies as being more salient in a refusal decision, these could be included as variables in the quantitative analysis.
The quantitative analysis may include one or both of the following components:
The study team will examine the extent to which the attributes of noncooperating jurisdictions differ systematically from the attributes of cooperating jurisdictions. This analysis will examine jurisdiction-level data available from DOL on the number of UI claims, number of first payments, and total benefits paid out on a monthly basis. The analysis will also consider differences across jurisdictions in the policies identified in the qualitative analysis.
Estimates from the Current Population Survey (CPS) can be used to compare the distribution of characteristics of the UI recipient population in responding jurisdictions to the full set of selected jurisdictions using the individual-level analysis methods described in the next subsection.17 Some of the characteristics available from the CPS include age, race/ethnicity, gender, occupation, and industry.
Each of these analyses can provide suggestive evidence on the extent to which jurisdiction-level response varies according to characteristics that are likely to be significant predictors of the outcomes of interest for this study. As such, the results from the nonresponse bias analysis could affect the study’s conclusions.
Substantive differences between cooperating and noncooperating jurisdictions, and/or strong associations between outcomes and nonresponse-relevant economic factors within the cooperating jurisdictions would indicate nonresponse that would be considered “informative,” relative to the potential outcomes of the sample members. Informative nonresponse would suggest a form of selection bias at the jurisdiction level, in which case it would not be reasonable to calculate fully nationally representative estimates using the survey sample. Multiple ways to analyze these data will be assessed. In one approach, the study team could seek to conduct design-based inference about a population of UI jurisdictions that the sample most closely resembles (that is, a population of UI jurisdiction with a similar distribution of the characteristics found to be significant in the analyses described above). In this case, inference could be based only on the main sample or on the entire augmented sample (including jurisdictions from the main and reserve samples), depending on the results of the qualitative analysis. Estimates based on this approach would be presented with appropriate cautions regarding the extent to which the findings can actually be generalized to such a population. Second, the study team could simply treat the entire augmented sample of cooperating jurisdictions as a convenience sample. In this case, statistical inference would be valid within the sample only, and the presentation of the findings would make it clear that estimates based on such an analysis do not generalize to any clear population.
If the quantitative analyses of jurisdiction-level nonresponse do not yield significant results (i.e., “uninformative” nonresponse), this suggests that selective nonresponse is less likely to introduce bias in the study’s findings. In this case, the study team would use the main or augmented sample (depending on the results of the qualitative analysis) to calculate national estimates. However, the study would explicitly acknowledge that (1) estimates could still be biased based on factors not accounted for in the quantitative nonresponse analysis and (2) the relatively small sample size of UI jurisdictions could limit the power of the quantitative analysis to reveal statistical differences. The findings of the study would include appropriate caveats for readers.
Nonresponse Bias Analysis at the Individual Level. As with almost any survey, some nonresponse among the UI recipients selected for the study is inevitable. Some sample members will not be located and others will not be able or willing to respond to the screening instrument or survey. The nonresponse bias analysis will use various data items in the administrative data files, including demographic information, employment status and quarterly earnings. The nonresponse bias analysis will consist of the following steps:
Compute response rates for key subgroups.
Compare the distributions of respondent and nonrespondent characteristics using initial sampling weights.
Identify the characteristics that best predict nonresponse and use this information to generate nonresponse weight adjustments.
Post-stratify survey estimates of the size of the study population to match national totals.
Compare the distribution of characteristics of respondents using the fully response-adjusted analysis weights to the distribution of characteristics of the full sample using the unadjusted sampling weights.
These bias analyses will build on the individual-level nonresponse analysis used to adjust the survey sampling weights to compensate for this nonresponse (see section 2). The analyses will be conducted within and across UI jurisdictions to assess whether the potential for nonresponse bias differs among jurisdictions. Each of these steps is discussed below in greater detail.
Compute response rates for subgroups. The response rate for the subgroups will be computed using the American Association for Public Opinion Research definition of the response rate: the weighted number of completed interviews with eligible participants divided by the estimated number of eligible individuals (AAPOR 2011). Overall response rates will be computed for the full sample and by jurisdiction. Response rates will then be computed for subgroups defined by characteristics available in the UI claims data to examine if these rates differ systematically from the overall response rate.
Compare the characteristics of respondents and nonrespondents. Next, the characteristics of respondents and nonrespondents will be calculated according to characteristics available in the UI claims data. The statistical significance of the difference between the respondent and nonrespondent subgroups will be assessed using t-tests. This type of analysis can be useful in identifying patterns of differences in observable characteristics that might suggest nonresponse bias, but it can be affected by small sample sizes and generally has low power to detect substantive differences. The large number of statistical tests conducted can also result in high rates of Type I error.
Identify the best explanatory factors of nonresponse and generate nonresponse weight adjustments. As described in section 2, logistic regression modeling is commonly used to develop adjustment factors for nonresponse. This approach is also known as response propensity modeling and can be viewed as an extension of the classical weighting-class nonresponse adjustment procedure that makes it possible to include more factors (that is, binary, categorical, and continuous factors) in nonresponse adjustments. A CHAID analysis will be used to assist in identifying potentially significant interactions among the subgroups or factors available for all individuals. The final response propensity model will use variables developed from the interaction terms identified in the CHAID analyses. Based on the final model, the inverse of the predicted propensity to respond will be used as an adjustment factor to the initial sampling weights.
Computing nonresponse adjustment factors will contribute substantially to the nonresponse bias analysis by identifying the main effects and interaction among main effects that are statistically associated with nonresponse. This information will be used in the bias analysis to form levels of categorical variables for computing response rates and point estimates using both the original sampling weights and the nonresponse adjusted sampling weights.
Post-stratify survey estimates to match available national totals. Post-stratification is a procedure whereby the response-adjusted weights are further adjusted so that survey estimates of the size of the study population are aligned to known totals external to the survey. This process offers face-validity for reporting population counts and has some statistical benefits. In this survey, there are no known population counts of each subpopulation of interest from an independent source so the study team will post-stratify to the population of UI recipients, for which population totals are known.
Compare the fully-adjusted weighted distribution of respondent characteristics to the distribution for the full sample using initial weights. In this last step, the distribution of respondent baseline characteristics will be compared to the distribution for the full study population and for key subgroups. This analysis can highlight measures where the potential for nonresponse bias is greatest and where greater caution should be exercised in the interpretation of the observed findings.
4. Tests of Procedures and Methods
The questionnaire for the COBRA Subsidy Study was pretested to assess the data collection process, evaluate the clarity of the questions asked, identify possible modifications to either question wording or question order that could improve the quality of the data, and estimate respondent burden. A pretest sample was chosen that closely mirrors the sample of UI recipients to the extent possible. Since a sample selected from UI administrative data files was not available for the pretest due to the timing and availability of sample data as well as contractual constraints related to using data collected for some other study, Mathematica solicited staff for referrals of friends and family members who received UI benefits during the time frame of interest. This approach had been used in the past with great success. By selecting pretest respondents who were unemployed in the same period as our targeted sample, Mathematica was better able to understand the recall problems sample members faced and improved our recall aids. Criteria for identifying pretest respondents were explicit. Pretest respondents were assured of the same level of privacy as other study participants.
Pretest interviews were monitored to identify questions that were problematic for interviewers or respondents, and interviewers debriefed each respondent after they completed their interview to gain additional insights. Mathematica’s survey director also conducted a debriefing session with interviewers upon completion of all pretests to get their perspective on how well the survey instrument worked and where improvements were needed. This intensive approach to debriefing pretest participants and interviewers allowed us to assess the effectiveness of approaches and instruments and identify where modifications were needed. This kind of debriefing had proven to be invaluable to similar data collection efforts. The pretests were conducted by telephone to mirror the planned data collection. However, hard-copy instruments were used since programming the pretest version was not an efficient use of resources. Pretest sample members received a $50 incentive payment for completion.
To test the IVR system, Mathematica’s central office and SOC staff will call the IVR system to assess how well the system works in terms of voice clarity, and the accuracy of data recording as well as its capacity to handle high-volume calling. Reports generated by the system will be reviewed to check the accuracy of data entered. The IVR system will be thoroughly tested to ensure that the data collected is recorded and transmitted accurately. As a further test, during data collection, some ineligible cases will be called back to verify that the IVR was properly implemented.
5. Individuals Consulted on Statistical Aspects of the Design
To ensure that the best decisions were made regarding the statistical aspects of the design, experts from outside the agency were consulted, and their input has helped to shape the sampling design. These experts included project staff from Mathematica and members of the project’s Technical Working Group. The experts consulted are listed below, along with telephone contact information. Only Mathematica staff will process and analyze the information collected.
Mathematica Staff
Dr. Anu Rangarajan, Project Director (609) 936-2765
Dr. Nathan Wozny, Researcher (609) 936-2795
Dr. Nan Maxwell, Senior Researcher (510) 830-3726
Dr. Frank Potter, Senior Fellow (239) 558-5956
Dr. Eric Grau, Senior Statistician (609) 945-3330
Dr. Hanley Chiang, Researcher (617) 674-8374
Members of the Technical Working Group
Dr. Randall Bovbjerg, Senior Fellow Health Policy Center,
Urban
Institute (202) 261-5685
Dr. Jonathan Gruber, Professor of Economics,
Massachusetts
Institute of Technology (617) 253-8892
Dr. Brigitte Madrian, Professor of Public Policy,
Harvard
University (617) 495-8917
Agency for Healthcare Research and Quality. Percent of
Private-Sector Employees Eligible for Health Insurance That Are
Enrolled in Health Insurance at Establishments That Offer Health
Insurance by Firm Size and Selected Characteristics: United States,
2009. Undated.
[http://www.meps.ahrq.gov
/mepsweb/data_stats/summ_tables/insr/national/series_1/2009/tib2a1.htm].
Accessed February 21, 2011.
American Association for Public Opinion Research (AAPOR). 2011. Standard Definitions: Final Dispositions of Case Codes and Outcome Rates for Surveys. Seventh edition. Deerfield, IL: AAPOR.
Berger, Mark C., Dan A. Black, Frank A. Scott, and Amitabh Chandra. “Health Insurance Coverage of the Unemployed: COBRA and the Potential Effects of Kassebaum-Kennedy.” Journal of Policy Analysis and Management, vol. 18, no. 3, 1999, pp. 430-448.
Biggs, David, Barry de Ville, and Ed Suen. “A Method of Choosing Multiway Partitions for Classification and Decision Trees.” Journal of Applied Statistics, vol. 18, no. 1, 1991, pp. 49–62.
Binder, D. A. “On the Variances of Asymptotically Normal Estimators from Complex Surveys.” International Statistical Review, vol. 51, 1983, pp. 279–292.
Bovbjerg, Randall R., Stan Dorn, Juliana Macri, and Jack Meyer.
Federal Subsidy for Laid-Off Workers’ Health Insurance: A
First Year’s Report Card for the New COBRA Premium Assistance.
Washington, DC: Urban Institute Health Policy Center, July 2010.
[http://www.urban.org/uploadedpdf
/412172-laid-off-workers.pdf].
Accessed August 31, 2010.
Bureau of Labor Statistics. “Employee Benefits in the United States—March 2010.” News release, July 27, 2010a. Retrieved February 21, 2011, from http://www.bls.gov/news.release/ pdf/ebs2.pdf.
Bureau of Labor Statistics. “The Employment Situation—August 2010.” News release, September 3, 2010b. [http://www.bls.gov/news.release/pdf/empsit.pdf]. Accessed September 8, 2010.
Chromy, James R. “Sequential Sample Selection Methods.” Proceedings of the American Statistical Association, Survey Research Methods Section, 1979, pp. 401-406.
Corson, Walter, Karen Needels, and Walter Nicholson. “Emergency Unemployment Compensation: The 1990s Experience Revised Edition.” Unemployment Insurance Occasional Paper No. 99-4. Washington, DC: U.S. Department of Labor, Employment and Training Administration, 1999.
Curtin, Richard, Stanley Presser, and Eleanor Singer. “Changes in Telephone Survey Nonresponse over the Past Quarter Century.” Public Opinion Quarterly, vol. 69, no.1, spring 2005, pp. 87-98.
Ebenstein, Avraham, and Kevin Stange. “Does Inconvenience Explain Low Take-Up? Evidence from Unemployment Insurance.” Journal of Policy Analysis and Management, vol. 29, 2010, pp. 111–136.
Employment and Training Administration. Comparison of State Unemployment Insurance Laws. April 6, 2010. Retrieved February 21, 2011, from http://www.ows.doleta.gov/ unemploy/comparison2010.asp.
Folsom, Ralph E., Francis Potter, and Steven R. Williams. “Notes
on a Composite Measure for Self-Weighting Samples in Multiple
Domains.” In Proceedings of the American Statistical
Association, Section on Survey Research Methods, Alexandria,
VA: American Statistical Association, 1987,
pp. 792-796.
Hirano, Keisuke, Guido Imbens, and Geert Ridder. “Efficient Estimation of Average Treatment Effects Using the Estimated Propensity Score.” Econometrica, vol. 71, no. 4, 2003, pp. 1161-1189.
Imbens, Guido. “Nonparametric Estimation of Average Treatment Effects Under Exogeneity: A Review.” Review of Economics and Statistics, vol. 86, no. 1, 2004, pp. 4-29.
Kapur, Kanika, and M. Susan Marquis. “Health Insurance for Workers Who Lose Jobs: Implications for Various Subsidy Schemes.” Health Affairs, vol. 22, no. 3, 2003, pp. 203-213.
Kass, G. V. “An Exploratory Technique for Investigating Large Quantities of Categorical Data.” Applied Statistics, vol. 29, no. 2, 1980, pp. 119–127.
Magidson, Jay. SPSS for Windows CHAID Release 6.0. Belmont MA: Statistical Innovations, Inc., 1993.
Needels, Karen E., Walter Corson, and Walter Nicholson. “Left
Out of the Boom Economy:
UI Recipients in the Late 1990s.”
Report submitted to the U.S. Department of Labor. Princeton, NJ:
Mathematica Policy Research, October 2001.
Rangarajan, Anu, Carol Razafindrakoto, and Walter Corson. “Study to Examine UI Eligibility Among Former TANF Recipients: Evidence from New Jersey.” Princeton, NJ: Mathematica Policy Research, 2002.
Research Triangle Institute. SUDAAN Language Manual, Release 9.0. Research Triangle Park, NC: Research Triangle Institute, 2004.
Robins, James, and Andrea Rotnitzky. “Semiparametric Efficiency in Multivariate Regression Models with Missing Data.” Journal of the American Statistical Association, vol. 90, no. 429, 1995, pp. 122-129.
Särndal, Carl-Erik, Bengt Swensson, and Jan Wretman. Model-Assisted Survey Sampling. New York: Springer-Verlag, 1992.
Schochet, Peter, Jillian Berk, and Pat Nemeth. “Short-Term Results of the New Survey Procedures for the TAA Evaluation.” Memo to Sande Schifferes. Princeton, NJ: Mathematica Policy Research, Inc., November 2008.
Sen, A. R. “On the Estimate of the Variance in Sampling with Varying Probabilities.” Journal of the Indian Society of Agricultural Statistics, vol. 5, 1953, pp. 119-127.
Stanton, Mark, and Margaret Rutherford. “Employer-Sponsored Health Insurance: Trends in Cost and Access.” Research in Action Issue 17. Rockville, MD: Agency for Healthcare Research and Quality, 2004.
Tuckel, Peter and Harry O’Neill. 2001. “The Vanishing Respondent in Telephone Surveys.” Journal of Advertising Research: 42: 26-48.
U.S. Census Bureau. Statistics About Business Size (Including Small Business) from the U.S. Census Bureau. Undated. [http://www.census.gov/epcd/www/smallbus.html]. Accessed September 8, 2010.
Yates, F., and P. M. Grundy. “Selection Without Replacement from Within Strata with Probability Proportional to Size.” Journal of the Royal Statistical Society Series B, vol. 15, 1953, pp. 253-261.
1 Individuals that experienced job loss between September 1, 2008 and mid-February 2009 will not be sampled even though some of these workers might have qualified for subsidies. Workers who lost jobs after September 1, 2008 and remained unemployed through February 17, 2009 would have qualified for subsidies. However, others who lost jobs after September 1, 2008, but became reemployed by February 17, 2009 and were eligible for a group health insurance plan through their employer were not eligible for the subsidy. Since subsidy eligibility during this window (for those who lost employment between September 2008 and mid-February 2009) is correlated with reemployment, a key outcome for this study, including this sample in our study could potentially introduce bias in the study’s impact analysis.
2 To ensure the comparability of the subsidy-eligible and subsidy-comparison groups, the timing of the periods from which people are sampled may be altered slightly based on economic conditions or individual characteristics based on findings from the analysis of the state UI claims data.
3 As noted in the next subsection, a small fraction of COBRA-eligible individuals who lose a job involuntarily do not apply for or receive UI. This may lead the estimates to understate the population sizes slightly. However, some individuals may have multiple UI records with a first payment, so that these individuals are counted more than once. The overall effect of these sources of error in the estimates is expected to be small.
4 Job losers whose base-period earnings are too low to meet the minimum threshold for UI eligibility might have worked part-time, or have had very low wages, or have exhibited a combination of these factors. All of these factors are associated with low rates of enrollment in employer-sponsored health insurance. Only about 11 to 14 percent of part-time workers have employer-sponsored coverage (Stanton and Rutherford 2004; Bureau of Labor Statistics 2010a), and 13 percent of workers in the bottom decile of hourly wages have employer-sponsored coverage (Bureau of Labor Statistics 2010a).
5 The estimated subsidy eligibility rate of 24 to 29 among UI recipients is based on the following evidence. First, 35 to 41 percent of UI recipients are projected to be COBRA-eligible. Specifically, of the 65 percent of UI recipients who are eligible for employer-sponsored coverage prior to job termination (Needels et al. 2001), 55 to 65 percent are assumed to have participated in their group plans (at a rate lower than the 77 percent participation rate for the general population of eligible workers reported by the Agency for Healthcare Research and Quality (n.d.). Of the job losers who participated in employer-sponsored coverage, 97 percent are assumed to have been in jobs covered by COBRA or mini-COBRA laws; this is based on estimates that 80 percent of employees work in firms covered by COBRA laws (U.S. Census Bureau n.d.), and, of the remaining 20 percent not covered by COBRA laws, 84 percent are assumed to have been covered by mini-COBRA laws (based on the calculation for the share of UI recipients in states with mini-COBRA laws). This yields a COBRA eligibility rate between 35 percent (=0.65*0.55*0.97) and 41 percent (=0.65*0.65*0.97) among UI recipients. Subtracting the one-fourth of COBRA-eligible unemployed people eligible for coverage under a spouse’s health plan (Berger et al. 1999) as well as small fractions (5 percent or less) who are eligible for Medicare or whose income exceeds the limits for subsidy eligibility, about 24 to 29 percent of UI recipients are expected to be eligible for the subsidy in the ARRA period.
6 The estimated subsidy eligibility rate in the general population is based on the following assumptions: 90 percent of U.S. households have an adult in the labor force; of the reference persons in these households, 9 percent experienced job separation during the ARRA period; of these, 92 percent experienced involuntary job loss (on the basis of the Bureau of Labor Statistics 2010b); of these, 30 percent had employer-sponsored health insurance at their most recent job (on the basis of Kapur and Marquis 2003); of these, 70 percent are subsidy-eligible (on the basis of Berger et al. 1999). Thus, an estimated 1.6 percent (=0.90*0.09*0.92*0.30*0.70) of households contain subsidy-eligible persons.
7 A separate OMB/PRA clearance package will be submitted for data collection for the UCP Evaluation.
8 The selection of UI jurisdictions will also be implicitly stratified according to geography using three strata based on DOL regions. The first stratum consists of UI jurisdictions in the Northeast, Mid-Atlantic, and South (regions 1, 2, and 3). The second stratum consists largely of states in the Rocky Mountains, the Texarkana area, the Great Plains, and the Midwest (region 5 and most of region 4). The third stratum consists of Pacific and Southwestern states (region 6 and New Mexico). Preliminary simulations of the sampling process suggested that this grouping structure could, on average, achieve a geographic balance across all of the DOL regions. Nonetheless, given that geographic stratification will occur after the sample of jurisdictions is divided into five primary analytic strata (as described in the text), the sampling process is unlikely to ensure an even allocation across regions (or geographic strata) in every sample.
9 Annual claims data are used, rather than monthly or quarterly data, to avoid having differences across states in the seasonality of unemployment affect the stratification variable.
10 Forming three or more PCC strata is not feasible because, when forming primary strata using both the PCC and MNW variables, over 60 percent of the jurisdictions selected for the analysis would be chosen with certainty, which has negative consequences for the precision and the face validity of the sample.
11 The sample frames from the ARRA and post-ARRA periods will be pooled separately in each state.
12 Matching methods provide an alternative approach to balancing the characteristics of the ARRA and post-ARRA samples. In the matching approach, each member of the UI recipient population in the ARRA period would be matched to the person in the post-ARRA period with the closest propensity score, and matched pairs would be randomly sampled. However, because persons in the post-ARRA period who were not involved in any match could never be selected, inferences about the full study populations in the post-ARRA period could not be made.
13 Some individuals who are truly in the subsidy-eligible or subsidy-comparison groups are expected to provide incorrect responses that cause them to be screened out. Therefore, although an estimated 25 to 29 percent of respondents are expected to be subsidy-eligible or subsidy-comparison, an estimated 21 to 25 percent will screen in. Similarly, some individuals might also get screened in when they should have gotten screened out. However, their responses to the more detailed questions in the full interview are expected to provide more accurate information regarding the correct population to which they belong.
14 Section 1 describes the size measure and sampling strategy that is predicted to produce nine certainty states. The projected certainty states will contain 42 percent of the sample based on the population estimates.
15 Additional adjustments may be made based on the findings of the nonresponse analysis described in section 3.
16 CHAID is normally attributed to Kass (1980) and Biggs et al. (1991), and its application in SPSS is described in Magidson (1993). Decisions about variables and interactions will be based on statistical tests with the significance level (alpha level) set to 0.30. The test size of 0.30 is used instead of the standard 0.05 because the purpose of the model is to improve the estimation of the propensity score and not to identify statistically significant factors related to response.
17 Measures derived from the CPS will be calculated using the sampling weights provided in that survey.
Draft iii
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | NWozny |
| File Modified | 0000-00-00 |
| File Created | 2021-01-31 |
© 2025 OMB.report | Privacy Policy