APPENDIX G. Common Assumptions for Statistical Models
APPENDIX G. Common Assumptions for Statistical Models_final.docx
Eval of SNAP Nutrition Edu Practices Study - Wave II
APPENDIX G. Common Assumptions for Statistical Models
OMB: 0584-0554
Appendix
G
C ommon
Assumptions for
ommon
Assumptions for
Statistical Models
Assumptions for Statistical Models of Parental Reports of Children’s Fruit and Vegetable Consumption in a Clustered, Experimental or Quasi-Experimental Design (INN and UKCES)
Sample size estimation procedures are used to quantify researchers’ level of confidence regarding their ability to accurately reject the null hypothesis when empirical differences are statistically significant. To achieve this end, a number of assumptions may be necessary. When information from previous studies or pilot studies similar to the study being planned is available, the potential validity of sample size estimation is improved. Without this information, researchers must rely on their best judgment and leverage their experience to identify reasonable values to justify sample sizes.
First, we must have an understanding of the distributional characteristic of the primary impact variables. Our main outcome measure and the focus of sample size estimation is the change in the number of cups of fruits and vegetables eaten by children participating in the program intervention, as reported by their parents or caregivers. We began with mean and standard deviation estimates from a trial in Chicago in which parents reported their children’s fruit and vegetable consumption. The study included six lower socioeconomic status communities and collected data from 516 parents on their young children’s dietary intake. In this study population, mean fruit and vegetable consumption was 3.83 servings per day, with a standard deviation of 2.04 servings (Evans, Necheles, Longjohn, & Christoffel, 2007). For our calculations, we applied the formula 1 cup = 2 servings to transform the mean and standard deviation into cup units.
Second, we must also have a reasonable expectation for the program’s impact, often referred to as the minimum detectable effect and indexed in terms of standard deviation units as the effect size. This number describes the anticipated change in observed outcomes among participants as a result of participating in the intervention. For our purposes, we assumed a change of 0.30 standard deviation units or greater. Based on the findings from the Chicago study, this suggests a realized change of 0.31 cups of fruit and vegetables from baseline values. This expectation is consistent with findings reported in a recent meta-analysis by Knai, Pomerleau, Lock, and McKee (2006) who found that across a range of dietary interventions, children’s fruit and vegetable consumption increased by 0.3 to 0.99 servings (i.e., 0.15 to 0.49 cups) per day.
Third, we needed an expression that accounts for the variance components at the individual and school levels. The intraclass correlation coefficient (ICC) provides an estimate of the proportion of variation in the endpoint attributable to the group over and above the variation associated with the individuals located within those groups. The ICC is combined with estimates of residual variance to determine within-group and between-group components of variation. We are unaware of any study that has published ICC estimates on parents’ reports of children’s dietary intake. However, Murray, Phillips, Birnbaum, and Lytle (2001) report ICCs of 0.02179 for fruit consumption and 0.02684 for vegetable consumption among a sample of middle school students. Given that the upper bounds of the 95 percent confidence interval around these estimates are 0.057 and 0.068, respectively, we anticipated the high-end range of ICC values to be 0.03 to 0.07 and used an ICC of 0.05 for the purpose of estimating statistical power.
Finally, we accounted for the characteristics of the analytic model. Our calculations are appropriate for a linear mixed model regression model that includes baseline and follow-up measures (i.e., pre- and post-test model) and allows for the inclusion of covariates associated with the outcome variable. Repeated measures and covariate adjustment can improve precision by minimizing variance components at the individual and school levels, as discussed in Murray and Blitstein (2003). We included the following adjustments:
r(yy)m = 0.60
r(yy)g = 0.70
θ(y)m = 0.10
θ(y)g = 0.00
Here r(yy) and θ(y) are reductions to variations for overtime correlation and inclusion of covariates, respectively, where, m represents level 1 (individual) and g represents level 2 (schools). We anticipated a larger r(yy) at level 2 because school means are likely to be more stable over time than individual means. Additionally, we assumed a small adjustment for inclusion of individual-level covariates but none for school level. This is a conservative approach. We may have some reduction in level 2 due to covariates. However, we are not planning to include school-level covariates because these reduce degrees of freedom for the test of the intervention effect.
Our sample size estimation procedures followed the convention of estimating sample size allowing for a Type II error rate of 0.20 (yielding 80 percent statistical power) and a Type I error rate of 0.05, with a two-tailed test.
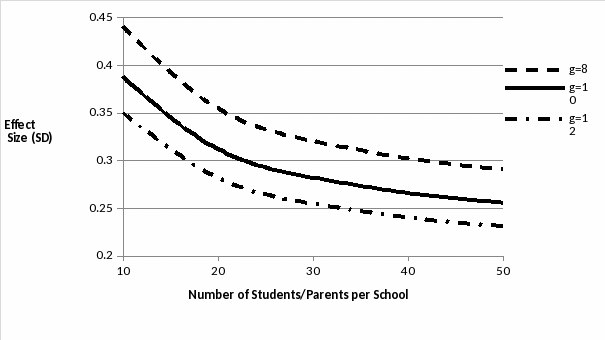
Figure G-1 provides power curves describing the number of schools and observations per school needed to identify intervention impacts. As this figure indicates, we are appropriately sized to identify program impacts of 0.30 SD or greater with 8 schools per condition and 40 students/parents per school, program impacts of 0.27 SD or greater with 10 schools per condition and 30 students/parents per school, and program impacts of 0.29 SD or greater with 12 schools per condition and 20 students/parents per school.
Figure G-1.—Power Curves Describing the Number of Schools and Observations per School Needed to Identify Intervention Impacts
Assumptions for Statistical Models of Self-Reports of Fruit and Vegetable Consumption by Seniors in a Clustered, Experimental Design (MSUE)
Sample size estimation for self-reported fruit and vegetable consumption among seniors followed the same steps and relied on many of the same assumptions detailed above. The distribution characteristics of the primary impact variables are similar. Our main outcome measure, and the focus of sample size estimation, remains the number of cups of fruits and vegetables consumed. Here, however, we are interested in self-reported consumption by seniors (aged 60 and above). We began with recent data that suggest that seniors report consuming approximately 1.735 (standard deviation = 0.98) cups of fruits and vegetables per day (Baker & Wardle, 2003; Juan & Lino, 2007; Greene, Fey-Yensan et al,. 2008). As with other SNAP nutrition education programs, we assumed a program impact of 0.30 standard deviation units, or 0.29 cups of fruits and vegetables per day.
Next, we needed an expression that accounts for the variance components at the individual and center levels. This was obtained through estimation based on the variance in the outcome variable and the ICC. Because data on ICCs among seniors are not available, we again assumed an ICC of 0.05 for the purpose of sample size estimation and included the following adjustments for repeated measures and covariates:
r(yy)m = 0.60
r(yy)g = 0.65
θ(y)m = 0.10
θ(y)g = 0.00
These expectations are similar to the expectations noted for parents and students in elementary schools. However, we took a slightly more conservative position on the benefits of repeated measures at the center level given current uncertainty regarding the make-up and characteristics of the pool of available centers. Our sample size estimation procedures followed the convention of estimating sample size allowing for a Type II error rate of 0.20 (yielding 80 percent statistical power) and a Type I error rate of 0.05, with a two-tailed test.
Figure G-2 provides power curves describing the number of centers and observations per center needed to identify intervention impacts. As this figure indicates, we are appropriately sized to identify program impacts of 0.30 SD or greater given any of the following conditions:
10 centers per condition with complete data from 45 seniors per center
12 centers per condition with complete data from 25 seniors per center
14 centers per condition with complete data from 18 seniors per center
16 centers per condition with complete data from 14 seniors per center
As can be seen by examining the spacing of the curves in Figure G-2, there is an interesting relationship between the number of centers and the number of seniors surveyed per center. As the number of centers increases, the needed number of seniors drops, but the gain demonstrates a pattern of diminishing returns. Given cost and logistical considerations, including a review of average center size and expectations regarding response and participation rates, we will work with MSUE to recruit at least 28 centers (yielding 14 centers per condition or greater) with an average of no less than 40 persons per center. This will provide a sample large enough to yield tests of intervention effects with a minimum of 80% statistical power.
Figure G-2.—Power Curves Describing the Number of Senior Centers and Observations per Center Needed to Identify Intervention Impacts

References
Baker, A. H. and J. Wardle (2003). "Sex differences in fruit and vegetable intake in older adults." Appetite, 40: 269-275.
Evans, W. D., Necheles, J., Longjohn, M., & Christoffel, K. K. (2007). "The 5-4-3-2-1 Go! Intervention: Social Marketing Strategies for Nutrition. " Journal of Nutrition Education and Behavior, 39(2, supplement 1), s55–s59.
Greene, G. W., N. Fey-Yensan, et al. (2008). "Change in fruit and vegetable intake over 24 months in older adults: Results of the SENIOR project intervention." The Gerontologist 48(3): 378-387.
Juan, W. Y. and M. Lino (2007). Fruit and vegetable consumption by older Americans. Nutrition Insight, 34. Center for Nutrition Policy and Promotion. Alexandria, VA, United States Department of Agriculture.
Knai, C., Pomerleau, J., Lock, K., & McKee, M. (2006). Getting children to eat more fruit and vegetables: a systematic review. Preventive Medicine, 42(2), 85–95.
Murray, D. M., Phillips, G. A., Birnbaum, A. S., & Lytle, L. A. (2001). Intraclass Correlation for Measures from a Middle School Nutrition Intervention Study: Estimates, Correlates, and Applications. Health Education and Behavior, 28(6), 666–679.
Murray, D. M. and J. L. Blitstein (2003). "Methods to reduce the impact of intraclass correlation in group-randomized trials." Evaluation Review 27(1): 79-103.
Resnicow, K., Smith, M., Baranowski, T., Baranowski, J., Vaughan, R., & Davis, M. (1998). "Two-year tracking of children’s fruit and vegetable intake." Journal of the American Dietetic Association, 98(7), 785–789.
.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Sharon Barrell |
| File Modified | 0000-00-00 |
| File Created | 2021-01-31 |
© 2026 OMB.report | Privacy Policy