APPENDIX E. Statistical Methods for Impact Evaluation
APPENDIX E. Statistical Methods for Impact Evaluation_final.docx
Eval of SNAP Nutrition Edu Practices Study - Wave II
APPENDIX E. Statistical Methods for Impact Evaluation
OMB: 0584-0554
Appendix E.
Statistical
Methods for the
Impact Evaluation
This appendix provides a detailed description of the statistical methods that will be used by the contractor, RTI International, for the impact evaluations of the three demonstration projects.
INN IMPACT EVALUATION
Respondent Universe and Sampling Methods
The population of interest is third grade students attending eligible schools in four Iowa school districts (Council Bluffs, Waterloo, Des Moines, and Davenport). Data on this population will be gathered through surveys of children’s parents and/or guardians about dietary behavior in the family home. In each school district, schools will be recruited to participate in the study by INN. Eleven schools will be recruited from Des Moines, 11 schools will be recruited from Davenport, and a total of 11 schools will be recruited from the combined list of eligible schools in Council Bluffs and Waterloo.
Procedures for the Collection of Information
Statistical Methodology for Sample Selection
Our evaluation of the INN BASICS and Pick a better snack™ nutrition education interventions is based on a quasi-experimental design. The study will include two active intervention conditions and one comparison condition. One of the active interventions includes the school-based BASICS curriculum (single channel); the other active intervention combines the school-based BASICS curriculum and the Pick a better snack™ social marketing campaign delivered in the community through grocery stores and supermarkets (multichannel). The application of a quasi-experimental design – rather than a fully randomized design – is driven by several factors including: (1) the implementing agencies’ pre-existing arrangements with school districts and nutrition educators and (2) the use of a county-wide intervention (e.g., the social marketing program) limits opportunities to randomize schools while maintaining a design in which children and parents from control/comparison schools would not be influenced by the intervention. The study will take place in the school districts of four counties purposively selected and assigned to treatment conditions based on prior working relationships with INN. The Waterloo and Council Bluffs school districts have been selected as the location for the single-channel intervention, the Des Moines school district as the location for the multichannel intervention, and the Davenport school district has been selected to serve as the comparison condition.
Because of logistical considerations, the selection of schools for inclusion in the 2012 school-year evaluation will not be possible until the end of the 2011 school year. Selection of schools for inclusion in the study will occur in two steps. In the first step, a list of schools that meet inclusion criteria will be generated in each district. Inclusion criteria will ensure that schools in the study meet FNS eligibility requirements and are large enough to meet student/parent level sampling needs. Second, we will review the lists (i.e., the universe) of available schools and the available data on each to determine whether a matching or stratification approach is likely to be beneficial. Matching and stratification processes are employed to ensure that potential confounds are similarly distributed across study conditions. Matching implies a one-to-one pairing of units based on an algorithm that summarizes all the schools in each district according to their measure on a confounding factor or set of factors and established similarity based on relative rank ordering. With stratification, the schools in each district are assigned to a category (i.e., strata) defined by measured values on a confounding factor or set of factors. Selection of a similar number of schools from each stratum putatively ensures that the exogenous factors are similarly distributed across study conditions.
Estimation and Analysis Procedures
We will assess the pre-intervention equivalence of the intervention and control groups based on statistical analysis of the pre-intervention survey data. We will examine categorical and continuous measures of demographic and socio-ecological variables using simple model-base methods that account for the correlated nature of the data and provide tabular results that include tests of association (e.g., t-tests, chi-square tests). In addition to demographic and socio-ecological variables, we will assess baseline levels for the key outcome measures. Factors that are significantly different will become candidate control variables for subsequent statistical assessment.
Given the limited number of units available for randomization in a group-randomized trial, it is common to use design characteristics such as matching and stratification to control potential confounding. Whether these features are then incorporated into analyses should be based on their value in helping to control random error. Other factors constant, simpler models offer greater statistical power. Design characteristics such as matching can provide greater statistical power (i.e., increased precision) only when they function to reduce random variation in the data.
Models that include design features such as matching and repeated measures will be compared to simpler models. As a first step, unadjusted statistical models involving the primary impact variable (cups of fruits and vegetables) will be run compared with the aim of identifying the model that provides the best linear unbiased estimate. This will be the model that combines the smallest standard error of the test in the intervention impact with the greatest number of degrees of freedom. The form of the impact model selected will be the one that reflects the highest level of precision and the least biased estimate. Once the form of the model is selected, we will look at the bivariate associations between outcome variables and treatment assignment. Program impact will be assessed through difference-in-difference, multivariate general, and generalized linear model analyses. As directed by our preliminary analyses, we will include control variables that are not well distributed across the intervention and control groups.
The analysis will be conducted using mixed-effect models that properly account for the complex and nested structure of the data. In our study, children are nested in schools, and schools are nested in conditions (intervention versus control), leading to sources of random variation at the school and individual levels; these sources will be accounted for in the model.
We will also investigate the potential impact of attrition on generalizability by comparing the pre-intervention similarity of study participants who provide post-intervention data (completers) and those who do not (attriters). This is accomplished by fitting logistic regression models that regress variables of interest on indicator variables that differentiate completers and attriters. This analysis provides odds ratios comparing completers with attriters on each variable, highlighting any association between a variable of interest and the likelihood of providing data at the post-intervention survey. If significant differences are found, a dummy indicator can be constructed to account for any bias that may be associated with attrition.
Degree of Accuracy Needed for the Purpose Described in the Justification
Table E.1 provides the sampling design for the evaluation of the INN BASICS and Pick a better snack™ interventions and our assumptions regarding response rate and attrition. We estimated sample size for a two-group comparison with a Type II error rate of 0.20 (yielding 80 percent statistical power) and a Type I error rate of 0.051. Our estimate is based on a two-tailed test, with the aim of detecting a change in consumption of servings of fruits and vegetables of 0.30 standard deviation units or better.
Table E.1.—Sample Design for the INN BASICS and Pick a better snack™ Evaluation
Group |
Number of Schools |
Estimated Number of Children* |
Number of Completed Surveys |
|
Pre-intervention Survey (Number of Parents/ Caregivers)† |
Post-intervention Survey (Number of Parents/ Caregivers)‡ |
|||
Single
Channel |
11 |
583 |
303 |
242 |
Multichannel (Des Moines) |
11 |
583 |
303 |
242 |
Comparison (Davenport) |
11 |
583 |
303 |
242 |
*
Assumes an average of 53 third-grade students per school.
†
Assumes that 65 percent will consent to providing contact
information and an 80 percent response rate for the
pre-intervention survey.
‡ Assumes an 80
percent response and retention rate between the pre- and
post-intervention surveys.
Appendix G provides our assumptions for sample size estimation; the assumptions include the minimum detectable effect, an estimate of the mean and standard deviation for the main outcome, estimation of intraclass correlation coefficients (ICCs), and reduction to the standard error due to characteristics of the statistical model (e.g., use of repeated measures, inclusion of covariates). Based on the characteristics of the BASICS program outlined above and the assumptions described in appendix G, our proposed sample design will provide an 80 percent probability of detecting a statistically significant difference if the realized increase in fruit and vegetable consumption is 0.27 cups of fruits and vegetables or greater. To the extent that we have overestimated the ICC or underestimated the benefits of correlated measures and covariate adjustment, statistical power will improve.
UNIVERSITY OF KENTUCKY COOPERATIVE EXTENSION SERVICE (UKCES) IMPACT EVALUATION
Respondent Universe and Sampling Methods
The population of interest is first through third grade students attending eligible schools in two Kentucky school districts. Ten schools in Laurel County and six schools in Perry County will be recruited to participate in the study; schools will be recruited by UKCES. Data will be gathered through surveys of children’s parents and/or guardians about dietary behavior in the family home. To avoid clustering within families we will conduct post-hoc examination of the survey data to identify parents who have more than one child attending a study school in the first through third grades. When this pattern is identified, a random selection process will be employed to select the index child who will be included in the analysis sample.
Statistical Methodology for Stratification and Sample Selection
Because of the sample size requirements detailed below, schools with fewer than 40 first- through third-grade students were removed from consideration prior to selection and randomization. All remaining schools were included in a simple random selection process; random selection was conducted for each county separately.
To control for potential differences between the two counties, schools were matched within county. One school from each pair was randomly selected to receive the intervention. Data provided by UKCES on school size (number of anticipated first- through third-grade students) and percentage of students receiving free and reduced-price meals (FARM) were used to create matched pairs. Matching was accomplished by using an algorithm that included these two variables—school size and percentage of students receiving FARM. The algorithm applies the following formula:
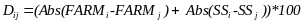 ,
,
where Dij is the distance value between two schools i and j, Abs indicates the absolute value, FARM indicates free and reduced-price meals, and SS indicates school size. For each school i, the lowest distance value to each school j is deemed the best match.
To
achieve the best set of matches, Dij is
calculated for each pair of schools, producing an i-by-j symmetric
matrix with values Dij on the principal
diagonal. Next, for each school, the lowest Dij
is identified, creating a column vector of Dij
scores. The lowest Dij
value representing the best matching pair is determined; these
schools constitute a matched pair and are removed from the pooled
list. The column vector of Dij scores is
recalculated among the remaining schools. Again the lowest Dij
representing the best matching pair is determined; these schools are
paired and removed. The process continues until all schools are
paired. This approach provides the lowest value for
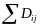 . When
there are an uneven number of schools, as in Laurel County, the
school remaining after the final pairing is dropped from
consideration for the study. Therefore, as a result of our matching
approach, Hunter Hills Elementary School in Laurel County will not be
included in the evaluation.
. When
there are an uneven number of schools, as in Laurel County, the
school remaining after the final pairing is dropped from
consideration for the study. Therefore, as a result of our matching
approach, Hunter Hills Elementary School in Laurel County will not be
included in the evaluation.
Next, one school in each pair was assigned a uniform random number (1 to 100). In pairs where the selected schools drew an even number, the selected school will receive the LEAP2 intervention, and the other school was assigned to the control condition. In pairs where the selected schools drew an odd number, the selected school was assigned to the control condition, and the other school will receive the LEAP2 intervention. Results of the assignment process are provided in Table E.2. Table E.3 provides additional detail, showing the anticipated number of children by grade for the treatment and control schools.
Table E.2.—Treatment and Control Schools Assignment for the Independent Evaluation of the UKCES LEAP2 Intervention
Intervention |
Control |
||||
|
Anticipated |
|
|
Anticipated No. of Students in 20111 |
|
School |
FARM (%) |
FARM |
School |
||
Laurel County |
|||||
East Bernstadt |
206 |
63 |
63 |
139 |
Johnson |
Camp Ground |
192 |
70 |
67 |
220 |
Colony |
Sublimity |
170 |
53 |
50 |
229 |
Bush |
Keavy |
151 |
73 |
80 |
172 |
Hazel Green |
Wayne-Pine |
291 |
54 |
68 |
343 |
London |
Perry County |
|||||
RW Combs |
122 |
84 |
81 |
107 |
Willard |
Chavies |
114 |
68 |
76 |
110 |
AB Combs |
DC Wooten |
221 |
64 |
56 |
235 |
Walkertown |
1 Anticipated numbers of students (grades 1–3) for school year 2011–2012 based on reported 2010 enrollment for students in grades K –2.
Table E.3.—Number of Children by Grade for Treatment and Control Schools for the Independent Evaluation of the UKCES LEAP2 Intervention
Intervention |
Control |
||||||
|
No. of 1st Graders |
No. of 2nd Graders |
No. of 3rd Graders |
No. of 1st Graders |
No. of 2nd Graders |
No. of 3rd Graders |
|
School |
School |
||||||
Laurel County |
|||||||
East Bernstadt |
64 |
64 |
78 |
42 |
51 |
46 |
Johnson |
Camp Ground |
58 |
81 |
53 |
89 |
61 |
70 |
Colony |
Sublimity |
59 |
49 |
62 |
89 |
69 |
71 |
Bush |
Keavy |
39 |
45 |
67 |
60 |
55 |
57 |
Hazel Green |
Wayne-Pine |
93 |
99 |
99 |
121 |
122 |
100 |
London |
Mean |
62.6 |
67.6 |
71.8 |
80.2 |
71.6 |
68.8 |
Mean |
SD |
19.5 |
22.5 |
17.7 |
30.4 |
28.9 |
20.2 |
SD |
Perry County |
|||||||
RW Combs |
44 |
39 |
39 |
36 |
35 |
36 |
Willard |
Chavies |
43 |
28 |
43 |
33 |
36 |
41 |
AB Combs |
DC Wooten |
71 |
78 |
72 |
80 |
89 |
66 |
Walkertown |
Mean |
52.7 |
48.3 |
51.3 |
49.7 |
53.3 |
47.7 |
Mean |
SD |
15.9 |
26.3 |
18.0 |
26.3 |
30.9 |
16.1 |
SD |
Estimation and Analysis Procedures
We will assess the pre-intervention equivalence of the intervention and control groups based on statistical analysis of the pre-intervention survey data. We will examine categorical and continuous measures of demographic and socio-ecological variables using simple model-base methods that account for the correlated nature of the data and provide tabular results that include tests of association (e.g., t-tests, chi-square tests). In addition to demographic and socio-ecological variables, we will assess baseline levels for the key outcome measures. Factors that are significantly different will become candidate control variables for subsequent statistical assessment.
Given the limited number of units available for randomization in a group-randomized trial, it is common to use design characteristics such as matching and stratification to control potential confounding. Whether these features are then incorporated into analyses should be based on their value in helping to control random error. Other factors constant, simpler models offer greater statistical power. Design characteristics such as matching can provide greater statistical power (i.e., increased precision) only when they function to reduce random variation in the data.
Models that include design features such as matching and repeated measures will be compared to simpler models. As a first step, unadjusted statistical models involving the primary impact variable (cups of fruit and vegetable) will be run compared with the aim of identifying the model that provides the best linear unbiased estimate. This will be the model that combines the smallest standard error of the test in the intervention impact with the greatest number of degrees of freedom. The form of the impact model selected will be the one that reflects the highest level of precision and the least biased estimate. Once the form of the model is selected, we will look at the bivariate associations between outcome variables and treatment assignment. Program impact will be assessed through difference-in-difference, multivariate general, and generalized linear model analyses. As directed by our preliminary analyses, we will include control variables that are not well distributed across the intervention and control groups.
The analysis will be conducted using mixed-effect models that properly account for the complex and nested structure of the data. In our study, students are nested in schools, and schools are nested in conditions (intervention versus control), leading to sources of random variation at the school and individual levels; these sources will be accounted for in the model.
We will also investigate the potential impact of attrition on generalizability by comparing the pre-intervention similarity of study participants who provide post-intervention data (completers) and those who do not (attriters). This is accomplished by fitting logistic regression models that regress variables of interest on indicator variables that differentiate completers and attriters. The results of this analysis provide odds ratios comparing completers with attriters on each variable, highlighting any association between a variable of interest and the likelihood of providing data at the post-intervention survey. If significant differences are found, a dummy indicator can be constructed to account for any bias that may be associated with attrition.
Degree of Accuracy Needed for the Purpose Described in the Justification
Table E.4 provides the sampling design for the evaluation of the UKCES LEAP2 intervention and our assumptions regarding response rate and attrition. We estimated sample size allowing for a two-group comparison with a Type II error rate of 0.20 (yielding 80 percent statistical power) and a Type I error rate of 0.052. Our estimate is based on a two-tailed test, with the aim of detecting a change in consumption of servings of fruits and vegetables of 0.30 standard deviation units or better.
Table E.4. —Sample Design for the UKCES LEAP2 Intervention
Group |
Number of Schools |
Number of Children* |
Number of Completed Surveys |
|
Pre-intervention Survey (Number of Parents/ Caregivers)† |
Post-intervention Survey (Number of Parents/ Caregivers)‡ |
|||
LEAP2 |
8 |
770 |
400 |
320 |
Control |
8 |
770 |
400 |
320 |
*
Assumes an average of 96 first- through third-grade students per
school.
† Assumes that 65 percent will consent
to providing contact information and an 80 percent response rate for
the pre-intervention survey.
‡Assumes an 80
percent response and retention rate between the pre- and
post-intervention surveys.
Appendix G provides our assumptions for sample size estimation; the assumptions include the minimum detectable effect, an estimate of the mean and standard deviation for the main outcome, estimation of ICCs, and reduction to the standard error due to characteristics of the statistical model (e.g., use of repeated measures, inclusion of covariates). Based on the characteristics of the LEAP2 intervention outlined above and the assumptions described in appendix G, our proposed sample design will provide an 80 percent probability of detecting a statistically significant difference if the realized increase in fruit and vegetable consumption is 0.27 cups of fruits and vegetables or greater. To the extent that we have overestimated the ICC or underestimated the benefits of correlated measures and covariate adjustment, statistical power will improve.
MICHIGAN STATE UNIVERSITY EXTENSION (MSUE) IMPACT EVALUATION
Respondent Universe and Sampling Methods
The study population is comprised of older adults (age 60 and up at the beginning of the intervention) who attend one of approximately 30 senior centers throughout the state of Michigan. For the purposes of this study, a senior center is defined as a facility that is open to the public and offers social services or support to seniors. The study excludes very small centers, housing or assisted living facilities, and locations that provide two or more meals per day to seniors. Because of logistical considerations, the selection of centers for inclusion in the evaluation will not be possible until spring 2011. Centers will be assigned randomly to a study condition (treatment versus control). Centers will be recruited by MSUE with the understanding that they must agree to the random assignment.
Procedures for the Collection of Information
Statistical Methodology for Stratification and Sample Selection
In order to provide a rigorous experimental design and avoid potential confounds, we will begin by reviewing the list of available centers. In addition to the number of centers available in each region, MSUE will provide details on the following characteristics:
Average number of seniors served per week,
Availability of meals at center, and
Number of meals served at the center per week.
We plan to implement the following sampling and allocation scheme:
Exclude assisted living facilities and centers serving more than one meal daily since seniors in these centers have limited opportunity for increasing the offering of fruits and vegetables at meal and snack time.
Exclude centers that report serving fewer than 30 seniors.
Stratify centers based on the five geographic regions (Central, North, Southeast, Southwest, and Upper Peninsula) and include at least one pair from each region to ensure statewide representation.
Where feasible, stratify within a region based on number of meals provided by centers.
Because each region has a small number of very large centers (serving 100+ seniors), we will remove these centers prior to randomization, stratify the group of large centers based on number of meals provided by centers, and randomize from within strata. Further, to maintain balance across centers at the individual level, we will randomly select a sub-sample of seniors from larger centers to participate in the study.
Estimation and Analysis Procedures
We will assess the pre-intervention equivalence of the intervention and control groups based on statistical analysis of the pre-intervention survey data. We will examine categorical and continuous measures of demographic and socio-ecological variables using simple model-base methods that account for the correlated nature of the data and provide tabular results that include tests of association (e.g., t-tests, chi-square tests). In addition to demographic and socio-ecological variables, we will assess baseline levels for the key outcome measures. Factors that are significantly different will become candidate control variables for subsequent statistical assessment.
Given the limited number of units available for randomization in a group-randomized trial, it is common to use design characteristics such as matching and stratification to control potential confounding. Whether these features are then incorporated into analyses should be based on their value in helping to control random error. Other factors constant, simpler models offer greater statistical power. Design characteristics such as matching can provide greater statistical power (i.e., increased precision) only when they function to reduce random variation in the data.
Models that include design features such as matching and repeated measures will be compared to simpler models. As a first step, unadjusted statistical models involving the primary impact variable (cups of fruit and vegetable) will be run compared with the aim of identifying the model that provides the best linear unbiased estimate. This will be the model that combines the smallest standard error of the test in the intervention impact with the greatest number of degrees of freedom. The form of the impact model selected will be the one that reflects the highest level of precision and the least biased estimate. Once the form of the model is selected, we will look at the bivariate associations between outcome variables and treatment assignment. Program impact will be assessed through difference-in-difference, multivariate general, and generalized linear model analyses. As directed by our preliminary analyses, we will include control variables that are not well distributed across the intervention and control groups.
The analysis will be conducted using mixed-effect models that properly account for the complex and nested structure of the data. In our study, seniors are nested in centers, and centers are nested in conditions (intervention versus control), leading to sources of random variation at the center and individual levels; these sources will be accounted for in the model.
We will also investigate the potential impact of attrition on generalizability by comparing the pre-intervention similarity of study participants who provide post-intervention data (completers) and those who do not (attriters). This is accomplished by fitting logistic regression models that regress variables of interest on indicator variables that differentiate participants who complete the program and those who do not (program dropouts). The results of this analysis provide odds ratios comparing nonparticipants with participants on each variable, highlighting any association between a variable of interest, the likelihood of completing the intervention, and providing data at the post-intervention survey. If significant differences are found, a dummy indicator can be constructed to account for any bias that may be associated with program dropouts.
Degree of Accuracy Needed for the Purpose Described in the Justification
Table E.5 provides the sampling design for the evaluation of MSUE’s Eat Smart, Live Strong intervention and our assumptions regarding response rate and attrition. We estimated sample size allowing for a two-group comparison with a Type II error rate of 0.20 (yielding 80 percent statistical power) and a Type I error rate of 0.053. Our estimate is based on a two-tailed test, with the aim of detecting a change in consumption of servings of fruits and vegetables of 0.30 standard deviation units or better.
Table E.5.—Sample Design for the MSUE Eat Smart, Live Strong Intervention
Group |
Number of Centers |
Number of Seniors* |
Number of Completed Surveys |
|
Pre-intervention Survey (Number of Seniors)† |
Post-intervention Survey (Number of Seniors)‡ |
|||
Eat Smart, Live Strong |
14 |
560 |
360 |
252 |
Control |
15 |
600 |
390 |
273 |
*
Assumes an average of 40 individuals per center will
participate in the evaluation study, which means we will need to
sample at the larger centers.
† Assumes that
65 percent will consent to participate in the pre-intervention
survey.
‡ Assumes a 70 percent response and
retention rate between the pre- and post-intervention surveys.
Appendix G provides our assumptions for sample size estimation; the assumptions include the minimum detectable effect, an estimate of the mean and standard deviation for the main outcome, estimation of ICCs, and reduction to the standard error due to characteristics of the statistical model (e.g., use of repeated measures, inclusion of covariates). Based on the characteristics of the Eat Smart, Live Strong program outlined above and the assumptions described in appendix G, our proposed sample design will provide an 80 percent probability of detecting a statistically significant difference if the realized increase in fruit and vegetable consumption is 0.29 cups of fruits and vegetables or greater. To the extent that we have overestimated the ICC or underestimated the benefits of correlated measures and covariate adjustment, statistical power will improve.
1 It is common among health prevention programs to apply a two-tailed test to assess intervention impacts. While a one-tailed test would yield greater power, we must consider that secular phenomena (e.g., extra-programmatic influences) could lead to reduction in children’s consumption of healthy foods.
2 It is common among health prevention programs to apply a two-tailed test to assess intervention impacts. While a one-tailed test would yield greater power, we must consider that secular phenomena (e.g., extra-programmatic influences) could lead to reduction in children’s consumption of healthy foods.
3 It is common among health prevention programs to apply a two-tailed test to assess intervention impacts. While a one-tailed test would yield greater power, we must consider that secular phenomena (e.g., extra-programmatic influences) could lead to reduction in consumption of healthy foods.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | SNAP–ED DRAFT REVISED STUDY PLAN |
| Subject | March, 23, 2009 |
| Author | lbell |
| File Modified | 0000-00-00 |
| File Created | 2021-01-31 |
© 2025 OMB.report | Privacy Policy