ADAM II Technical Documentation Report

Beginning in 1997, the National Institute of Justice (NIJ) began redesigning their decade-long data collection program, called Drug Use Forecasting (DUF), to orient the program towards a more scientifically sound foundation. The redesign led to a new data collection program, Arrestee Drug Abuse Monitoring (ADAM). The revised program introduced probability-based sampling at the facility and arrestee level as well as new instrumentation, and also added sixteen new survey sites. The new collection series was initiated in 23 sites in January 2000. After sponsoring quarterly data collection and expanding further to 35 sites, NIJ terminated ADAM due to budget cuts in 2003. Recognizing the important of the data series, in the fall of 2006, the Office of National Drug Control Policy (ONDCP) revived the ADAM program (ADAM II) in ten of the former ADAM data collection sites. ADAM II retained all of the original ADAM instrumentation, sampling, and data collection protocols, and added innovative estimation procedures, imputation methods and trend analysis. From 2007 to 2011, ADAM II collected data over two 14-day data collection periods in the ten sites^¹. In 2012, due to federal budget cuts, the number of sites was reduced to five and a single 21- day data collection period was instituted.

This report documents the ADAM II sampling procedure, data collection protocol, quality control procedures and estimation methodology employed in the five ADAM II sites in 2012. Procedural changes in the 2012 cycle were limited to a shorter total number of days for the data collection period (21 days instead of 28 days) and the elimination of one of the collection cycles (one quarter of collection instead of two quarters). Although the reader may question differences between trends moving to the one-time administration in 2012, the estimates with earlier years are comparable since the estimator adjusts for seasonality. In Washington DC, where no interview data were collected in 2012, we were able to use D.C. Pretrial Services urinalysis data to provide estimates of drug use only.

Allowing for comparisons over the 2000-2003 and 2007-2012 time periods, ADAM II uses the same template for sampling and data collection across all sites as ADAM did. Similarly, instrumentation has remained the same since 2000, as well as the general approach to sampling facilities within a county (the estimation catchment area) and arrestees within each facility. Original methodological templates were based on an analysis of data on operations and arrestee movements in one site (Portland, Oregon) in 1999. Some aspects of the methodological template have been modified over the years to adapt to specifics at a site (i.e., lags times from entry into a facility and availability for interviews), but these adaptations are often minor. For example, certain sites provide booking data that are more detailed than the booking data from other sites. Consequently, the estimation methodology takes advantage of greater detail where available, and accommodates lesser detail where necessary.

Some adaptations are more involved; as a result of multiple rounds of changes in police booking practices, data collection practices in Washington, D.C. demanded an involved methodological adaptation. In the second quarter of 2010 D.C. police stopped booking arrests in seven roughly equivalent sized districts and began booking all arrests at the Central Cell Block facility. Hence, data collection moved from each of the districts to the Central Cell Block facility. In the first quarter of 2011, police reverted to district booking for all misdemeanants, prompting another change in data collection. Thus, throughout 2011, ADAM II data for D.C. were collected for one week in the Central Cell Block facility and for one week in local districts. In addition, D.C. estimations use urine test data from D.C. Pretrial Services. In 2012, Washington, D.C. was not selected as an ADAM II collection site. Nonetheless, we continued to use the D.C. Pretrial Services drug test results, as they can provide an estimate of use (see Section 4.2), if appropriately methodologically adapted; We weighted the Pretrial Services data to the booking population and maintained the same protocol for using pretrial services data. Thus, there is a control for mistaking changes in the trends which might otherwise be a consequence of design changes.

This report does not attempt to document or explain all adaptations of the generic sampling procedure, quality control procedures and estimation methodology. The authors felt that since the explanation of the generic approach itself is complex, burdening readers with details about continuously evolving adaptations would detract from this report’s objective—namely, explaining the overall ADAM II methodology. However, it is important to document those adaptations for those interested in the research community so the ADAM II project maintains catalogued files of data and annotated computing software that meet professional standards for documentation. Those electronic documentations are available by request.

Section 1 explains ADAM II sampling procedures. As in ADAM, ADAM II sites were selected purposefully, so they do not represent a random sample of counties across the United States. Within each site, ADAM II represents all but very small booking facilities in the county; and within each booking facility, ADAM II selects a systematic sample of arrestees that mimics a random sample with unequal sampling probabilities.

Section 2 explains ADAM II data collection protocols. It identifies four data collection sources used to identify the sampling frame: the ADAM II interview, the associated urine test, the face sheet completed during sample selection and the booking census data. This section explains how ADAM II interviewers sample arrestees, approach them for interviews and replace sampled arrestees who are unavailable or who refuse the interview.

Section 3 explains case weighting and propensity scores. This section explains the logic of using propensity scores and describes the diagnostic tests applied to each site to assure that the inverse of the estimated propensity scores produces acceptable sampling weights.

Section 4 explains the ADAM II approach to imputation. Urinalysis results are sometimes missing, either because a respondent refuses to provide a urine specimen following his interview or because the respondent is unable to provide a urine specimen. ADAM II uses imputation routines to estimate the proportion of arrestees who would have tested positive for a specific illegal drug had all arrestees been tested.

Section 5 explains point prevalence and trend estimation for 2012. Except for data imputation, calculations of point prevalence estimates are straightforward given sampling weights. Because of the need to control for extraneous factors that may account for changes in the proportion of arrestees testing positive for illegal drugs, trend estimation proves to be more complicated.

Section 6 provides some concluding comments regarding the technical challenges addressed in ADAM II.

The ADAM II 2012 Sample

The original 35 counties in the ADAM from 2000-2003 were selected through a competitive grant process sponsored by NIJ. Consequently, the counties did not constitute a probability-based sample of US counties. In 2007 for ADAM II, ONDCP selected 10 counties from the original 35 based on geographic distribution (to represent different regional drug use) and adequacy of prior data (complete quarters of collection from 2000-2003).

In 2012, ADAM II had to limit collection to 5 of those 10 counties, but continued to provide estimates and trend analysis for those 5 counties. In addition, in 2012, the data collection period was reduced to one 21-day collection period in the second calendar quarter of the year instead of two 14-day data collection periods in the second and third calendar quarters, as was true from 2007-2011. As mentioned in the introduction, the trend estimates are not affected by the move to one collection period thanks to a control for seasonality.

While ONDCP wished to retain all sites, it was necessary to develop some criteria for site selection. The retention of 5 of the 10 sites was based on case production and response rates, cost efficiency and geographic representation of drug use patterns. ONDCP wanted to retain at least one southern site (Atlanta or Charlotte) and one Western site (Sacramento or Portland) so that the unique drugs use of those areas of the country were represented. The final selection resulted in the following sites for the 2012 collection: New York, NY (Borough of Manhattan); Atlanta, GA (Fulton County); Chicago, IL (Cook County); Denver, CO (Denver County) and Sacramento, CA (Sacramento, County). While we did not conduct interview in 2012 in the booking facilities in Washington, D.C., we used urine test data from the D.C. Pretrial Services agency to provide some estimates of prevalence of use for Washington, D.C.

While in ADAM and ADAM II the counties comprise a non-probability sample of counties, the sample of arrestees constitutes a probability-based sample of arrestees booked into jails within those counties. The sampling of facilities and arrestees is described in sections that follow.

Sampling Facilities Within Counties

Most ADAM II counties have a single jail or central booking facility where all county arrestees are booked pending further processing.^² The other ADAM II counties have multiple booking facilities, ranging from very small entities booking only a handful of arrestees (as in Hennepin County, MN) to booking facilities of equivalent size to the central county facilities (as in the Atlanta Detention Center). Where there are multiple jails, those small jails are excluded from the study, and the sampling frame comprises arrestees booked into large jails. Within an ADAM II site, each of the large jails is treated as a stratum, and a random sample is drawn from each stratum.

For example, in New York (Borough of Manhattan) there is a smaller municipal court ( the Midtown Community Court or MCC) where a subset of misdemeanant arrestees are taken for booking; the Midtown Community Court deals with what are often called “quality-of-life” or “nuisance” crimes such as farebeating, prostitution, vending without a proper license, shoplifting, public drunkenness ,and vandalism. While many offenders in these charge categories are also found in the main Manhattan criminal court facility, officers have the ability to deliver misdemeanants who are willing to plead guilty to their crimes to the MCC. The MCC arraigns approximately 200-300 persons per week compared to the over 1000 adult male offenders arraigned in the main Manhattan Criminal Court where ADAM II collects data. In another example, the ADAM and ADAM II samples in Chicago (Cook County) sample have always been somewhat different than in other sites. Cook County has multiple law enforcement agencies within the city of Chicago and in the county outer areas---the city has over 100 police precincts and the county holds nine suburban bond courts that process misdemeanor cases. The Cook County Jail (where ADAM II collects data), however, is where all those charged with felonies or serious misdemeanants in the county are transferred for processing. Therefore, the Chicago sample is limited to those moving through the large Cook County Jail--- all city and county felony arrests and serious misdemeanor arrests. In Atlanta (Fulton County) there are two principal booking facilities of approximately the same size. One (Atlanta Detention Center) is a facility where the Atlanta Police Department (APD) books all misdemeanants. The other (Fulton County Jail) is a large county facility where the APD books all felons and county law enforcement books both all felons and misdemeanants.^³

Small facilities in these sites might be represented by using cluster sampling, but this is impractical. Each small booking facility processes so few arrestees that without an excessive expenditure of project resources, interviewers are unable to gather data from anything more than a small, and consequently uninformative, sample of arrestees within the designated time frame. Not representing small facilities does not alter prevalence estimates materially because small facilities account for a small proportion of the counties’ bookings. Furthermore, exclusion of small facilities does not affect trends, provided it is understood that the trends pertain to those jails that are included in the sample.

In 2012, ADAM II interviews arrestees over 21 consecutive days in every sampled jail with the exception of Atlanta. In Atlanta, ADAM II samples from one facility for 11 days (the slightly higher volume facility) and 10 days in the other facility (the slightly lower volume facility).

Sampling Arrestees Within Facilities in each County

Although arrests are made and arrestees are brought into booking facilities 24 hours a day, it is neither logistically or financially feasible to station interviewers in booking facilities twenty-four hours per day for an extended data collection period. Recognizing this constraint, the original ADAM redesign team considered a plan to randomly sample periods or shifts during a twenty-four hour day, stationing interviewers in the jails during those sampled periods. This plan proved impractical for several reasons. First, jail personnel both prohibit interviewing of inmates during certain periods and require standard scheduling to minimize disruption of operations. ADAM II interviewing occurs in the active booking areas of booking facilities and by definition is somewhat disruptive to the regular law enforcement routine. Consequently, as “guests” in those facilities the research team must be as accommodating as possible. Second, sampling periods of relative quiescence force interviewers to be idle for at least some parts of their work shifts.

Consequently, the sampling design developed for ADAM and continued in ADAM II in each facility divides the data collection day (and the interview cases) into periods of stock and flow. Interviewers arrive at the jail at a fixed time during the day, typically the eight hours from 4 PM to 11 PM each day. Call this H. They work a shift of length S. The stock comprises all arrestees booked between H-24+S and H, and the flow comprises all arrestees booked between H and H+S. For example, if interviewers start working at 4 PM and work for 8 hours, then the stock period runs from 12PM to 4PM, and the flow period runs from 4PM to 12PM. Cases are sampled from the stock and flow strata.

In the stock period, sampling is done from arrestees who have been booked between H-24+S and H. This sampling begins at time H, and while arrestees identified as having been brought in during that time remain in the sample frame, interviewers can only interview those arrestees who remain in jail as of time H. In the flow period, sampling is done continuously for arrestees as they are booked between H and H+S.

To determine sampling rate, supervisors examine recent booking data from the facility, i.e., the number of bookings that occur during the stock and flow periods based on data for each facility reflecting the 21 day period prior to the quarter’s collection. Call the daily total N; call the number booked during the stock period N_S; and call the number booked during the flow period N_F. Then 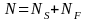. Supervisors set goals for sampling from the stock and flow for each site equal to n_Sand n_F, respectively, such that:

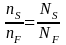
The actual sample size (n=n_S+n_F) depends on the number of interviewers and sometimes (for small jails) the number of bookings (N=N_S+N_F), since n cannot exceed N. Interviewers continue to sample and interview to the end of the shift period even when the tentative goals have been achieved.

The Lead Interviewer (LI) who serves as on-site sample manager lists arrestees according to when they were booked. With the intention of sampling n_s arrestees from N_s arrestees, the LI identifies n_s sequential strata with approximately N_s/n_s arrestees per strata.

The LI randomly selects the m^th arrestee in the first stratum and systematically selects the m^th arrestee in each of the remaining n_s-1 strata. If the sampled arrestee is unavailable or unwilling to participate, the supervisor selects the nearest temporal neighbor—meaning the arrestee whose booking time occurs immediately after the arrestee who is unavailable or who declined. Replacement continues until an arrestee is interviewed. Because of administrative practices of jails and courts, arrestees are frequently unavailable to interviewers, i.e., they have been transferred to another facility, have already been released or are in court. The selection of the nearest neighbor is intended to reduce or eliminate any bias that otherwise would occur from apparently low response rates. All cases sampled remain part of the sample for overall response rate calculations.

During the flow period, the supervisor selects the arrestee booked most recently and assigns an interviewer. If the arrestee is unavailable or unwilling to participate, the LI selects the next most recently booked arrestee as a substitute. This process continues until the workday ends at time H+S.

This procedure produces a sample that is reasonably well balanced, meaning that arrestees have about the same probability of being included in the sample. If the sample were perfectly balanced, weighting would be unnecessary for unbiased estimates; and, in fact, estimates based on weighted and unweighted ADAM data are similar. The sample is not perfectly balanced, however, for several reasons.

First, while LIs attempt to sample proportional to volume during the stock and flow periods based on recent data from the facility, achieving this proportionality requires information that is not available at the time that quotas are set. Analysts can only estimate N_S and N_F based on recent historical experience; furthermore, the LIs cannot know the length of time required to complete each interview because the length of the ADAM II interview depends on the extent of the arrestee’s comprehension and cooperation level, as well as the extent of his reported drug use and market activity. Hence, the achieved value of n_F is variable.

Second, the number of bookings varies from day-to-day, but the number of interviewers working each day based on historical data is constant. Days with a high number of bookings result in lower sampling probabilities than do days with a low number of bookings. Furthermore, the number of bookings varies over the flow period, so that arrestees who are booked during periods with the most intensive booking activity have lower sampling rates than do arrestees who are booked during periods with the least intensive booking activity. Sampling rates do not vary as much across the stock period because of the way that the period is partitioned.

Third, and perhaps most importantly, arrestees can exit the jail during the stock period. The probability that an arrestee has been released prior to being sampled depends on both the time during the stock period when he is booked and his arrest charges. The earlier that booking occurred during the stock period, the greater the opportunity he has had to be released. The more serious the charge, the lower the probability of being released, because serious offenders are more likely to be detained pending trial or require time-consuming checks for outstanding warrants. Neither factor plays an important role during the flow period because of the way that the sample is selected.

Data Collection Protocol

Data collection protocols are described in detail in the annual ADAM II reports (2007-2012) available through ONDCP’s website. The protocols are briefly summarized here to provide some context for the discussion of weighting and estimation methodologies.

Selecting Study Subjects

Interviewers work in teams in each jail. As discussed in Section 1, the supervising interviewer, a specially trained Lead Interviewer (LI), samples from the stock and flow and assigns interviewers to each case. The stock sample is generated from a list of all individuals booked since the interviewer’s last work period and is obtained from facility records each night. Not all arrestees are still in the facility, but who is there and who has left is not known at the point the stock sample is drawn. The LI requests an officer to bring the sampled arrestee to the interview area, and, if that arrestee is unavailable or unwilling to be interviewed, the LI records the reason and draws a replacement from the sample list. Sampling from the flow requires a list of individuals as they are booked into the jail. Throughout the data collection shift the LI continuously compiles a list of incoming arrestees and seeks the most recently booked arrestee. If that arrestee is unavailable or unwilling to be interviewed, the LI records the reason and seeks the closest temporal replacement.

For any arrestee sampled (regardless of their availability), the LI completes a face sheet based on facility records. The face sheet contains sufficient identifying information to allow the arrestee to be matched with “census” data (that is, a census or records representing all bookings into the jail in each of the 21 data collection days) that are collected long after sampling. The role of the census data is described in Section 2.2. The LIs use the facesheet to record that an interview occurred, and, if it did not, the reasons why it did not. Analysts use the facesheet to compute response rates. Bar-coded labels are attached to the facesheet, the interview form and a urine specimen bottle, tying all data together. All arrestees sampled have a facesheet, but not all have the other components of the collection (interview, urine specimen). To be eligible for interview, an arrestee must be: male, over 18, arrested no longer than 48 hours prior to the interview^⁴, coherent enough to answer questions and not an immigration or Federal Marshalls’ hold.

Arrestees who consent are interviewed for 15-20 minutes on average. The interview is the source of self-report ADAM II data. The request for a urine sample is made at the beginning of the interview and repeated at its completion. If the arrestee consents, he is given a specimen bottle which he takes to a nearby lavatory to produce a sample. The bottle is returned to the interviewer, stickered with a barcode, bagged and sent at the end of the shift to a national laboratory for testing. In most sites over 80% of arrestees consent to provide a urine specimen.

The Role of Census Data in Developing
Case Weights

Developing propensity scores for case weighting requires complete data on all bookings (a census) that occurred in each ADAM II facility during the 21-day period of data collection. These data are provided by each law enforcement agency participating in ADAM II after their data collection is completed. Site law enforcement partners submit census data in a variety of forms: electronic files listing each case, PDF, or other text files of cases and paper format listing all cases. The Abt Data Center staff transforms each into site and facility specific data sets containing the following data elements for each arrestee:

Date of Birth and or Age
ID (computer generated number)
Charges
Time of arrest
Time of booking
Day of arrest
Race

All data are transformed into a SAS dataset. The census data represents the sampling frame. As noted, ADAM II interviewers complete a facesheet that includes the above variables for every arrestee sampled for the study, information on whether the arrestee answered the interview and whether he provided a urine specimen.

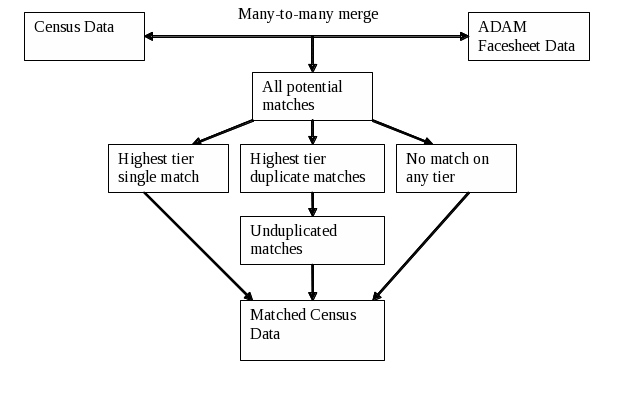
Figure 1 represents the steps included in the manipulation of the raw census data done in preparation for matching with the ADAM II facesheet data. The raw census data received from booking facilities are cleaned to correct invalid data and reformatted for compatibility with the other data components. The census data typically have one row of data per charge and must be converted to single records identifying arrestees with multiple charges. First, arrestees in the census data that are ineligible for the ADAM II survey are excluded: juveniles, women and people booked on days other than those when ADAM II surveys were conducted. Second, charges recorded in the census data are converted into a set of standardized ADAM II charges and the top severity, top charge and top charge category (violent, property, drug, other) are determined for each individual.

Figure 1: First Step in Matching Process

Figure 2 shows the process of matching the census records to the ADAM II facesheet records. The variables common to both the facesheet and the census data used to match the records are:

booking date/booking time
date of birth
arrest date/arrest time
charges
race.

Potential matches are outputted if records match on any single key variables; they are then ranked into tiers based on the goodness of the fit. For example, a facesheet record that matches a census record on just booking date/booking time and charges will be superseded in rank by a facesheet-census match that links on booking date/booking time, charges and date of birth. Out of all the potential matches the best census match is selected for each facesheet. If, in fact, multiple census records match the same facesheet, and these duplicate matches have equivalent rankings, booking date/time is used as a tiebreaker. The output dataset from this process is a one-to-one match between each facesheet record and census records.

Rarely, a facesheet fails to match any booking record. When this happens, a pseudo-booking sheet is created and inserted into the booking data. This process is represented by the right-hand flow in Figure 2.

Figure 2: Matching Census with Facesheet Data

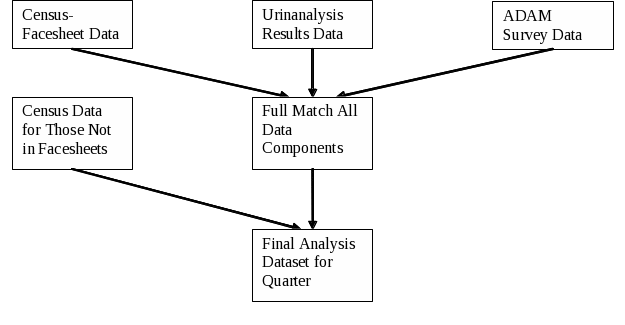
Figure 3 demonstrates the last step in the construction of the analysis file for each site and each data collection period. The linked census-facesheet data are merged with the appropriate urinalysis and survey record using unique identification numbers recorded in barcoded labels on the facesheet, interview, and urine specimen. The result is the final analysis dataset for each period for each particular ADAM II site.

Figure 3: Creation of Final Analysis File

Weighting the ADAM II Sample

The original ADAM program (2000–2003) used post-stratification weighting of cases. This meant that after the data have been assembled, analysts stratified the sample in each site according to jail, stock and flow, day-of-the-week and charge. The sampling probability was the number of interviews completed within each stratum divided by the number of bookings that occurred in that same stratum. Weights were the inverse of the achieved sampling probabilities. Although post-stratification may seem straightforward, weighting was time-intensive and uncertain. The resulting strata sometimes had empty cells or so few observations that one stratum had to be merged with one or more other strata.

To increase the validity of the weights and to reduce standard errors of the estimates, ADAM II adopted propensity score weighting. This section explains the logic of using propensity scores to weight survey data.

The Logic of Weighting with Propensity Scores

Unlike what is true when cases are drawn from a simple random sample, In ADAM II sampling probabilities vary systematically with features of the data: the individual’s arrest charge, the number of bookings on the day of collection, and time of day the individual is booked. Logistic regression is used to estimate the probability of appearing in the sample conditional on these features of the data. Consistent with the professional literature, predictions based on the logistic regression are called the estimated propensity scores. The inverse of the estimated propensity score provides a weight that, when applied to sample data, provides consistent estimates of drug use and other behaviors for the population of arrestees.^⁵

The use of propensity scores dates to work such as Rosenbaum (1984) and Rosenbaum and Rubin (1984). Rotnitzky and Robins (1995), among others, proposed using “inverse probability weighting” as a solution for missing data problems, of which sampling provides an illustration. Wooldridge (2003) proposed a generalized two-step estimation method, which produces consistent and asymptotically normal estimates. This method estimates propensity scores (i.e., probabilities of being sampled) in the first step, and uses inverses of the estimated propensity scores as weights when estimating the parameters of interest in the second step.

However, estimating standard errors is complicated using the two-step estimators. In ADAM II, relying on Wooldridge (2003), standard errors are programmed in STATA and SAS and the results from that programming are used when estimating preliminary ADAM II population statistics. The ADAM II experience is that the adjustment to the sampling variance is immaterial, and users can apply these weights without fear that the sampling variance is too high.^⁶

The use of propensity scores is a rapidly developing research topic, and some authors consider the methods for estimating standard errors as unsettled. Most survey applications currently in use appear to ignore the apparently minor variance inflation that occurs because of two-step estimation, and that is the ADAM II approach. As noted, however, the risk of materially understating standard errors appears minor, and estimators will be modified as estimation routines evolve.

Development of Propensity Scores

The following discussion uses original ADAM data from Portland for 2000 and 2001 as an illustration of estimating and testing propensity score weights for a single jail. Because the 2000 and2001 data were readily available, they were originally used to develop estimation routines, including diagnostic tools, that were then adapted to each of the other nine sites. As we will explain later, those estimation routines and diagnostic tools were used to reweight the original ADAM data for 2000 and 2001 and to weight all ADAM II data going forward.^⁷ Section 3.3 describes an adaptation to the weighting procedure implemented in 2011. The diagnostic routines are repeated for each site each quarter. The diagnostic output for ADAM II sites is voluminous and we do not report it here, but electronic documentation is available upon request.

Throughout the notation used in this section, the subscripts reference the i^th arrestee who was booked during the k^th half-hour on the j^th day of year t. The index k runs from 1 to 48 beginning at the thirty-minute period immediately after midnight.

S_ijkt This is a dummy variable coded 1 if the i^th arrestee who was booked during the k^th half-hour of the j^th day of year t was included in the sample. It is coded zero otherwise.

ST_ijkt This is a dummy variable denoting that the arrestee was booked during the stock period.

FL_ijkt This is a dummy variable denoting that the arrestee was booked during the flow period.

H_ijkt This is a dummy variable representing the half-hour during which the arrestee was booked.

FEL_ijkt This is a dummy variable coded 1 if the arrestee was charged with a felony and coded 0 otherwise.

MIS_ijkt This is a dummy variable coded 1 if the arrestee was charged with a misdemeanor and coded 0 otherwise.

OTH_ijkt This is a dummy variable coded 1 if the arrestee was charged with neither a felony nor misdemeanor and coded 0 otherwise.

NS_jt This is the number of bookings that occurred during the entire stock period of the j_th day of year t.

NFH_jkt This is the number of bookings that occurred during the k_th half-hour on the j_th day of year t.

Q_qt This is a dummy variable coded 1 if the arrestee was booked during the q_th quarter of year t.

To estimate the propensity score, a logistic regression is estimated with the logit:

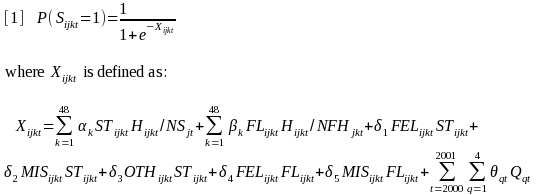
This model is used to estimate weights for the ADAM II samples (2007-2012), and to estimate new weights for the 2000 and 2001 ADAM sample. The reason for estimating new weights for 2000 and 2001 is that the propensity score estimator is an improvement over the post-stratification weighting procedure used previously. Since the propensity score is estimated using all available data, computing new weights for 2000 and 2001 is not an additional burden. In trend estimations (discussed in a Section 5), ADAM II utilizes the reweighted data (2000-2001), but has to rely on the only weights available for 2002-2003, the original post stratification ADAM weights.

The model specification requires some explanation. While [1] is the general specification used across the sites, site-specific changes are often made to this specification. Typically, the specification is modified because offenses appear to be coded differently across the years, so the felony/misdemeanor/other distinction cannot always be identified. When data allow, race and age are included in the construction of propensity scores.

The term appears in this model to account for variation in the sampling rate during the stock period. Because the quota n_S is invariant while NS varies over the sampling period, the probability of being interviewed during the stock period changes from day-to-day, depending on the number of bookings during that day’s stock period. Hence, NS_j appears in the denominator. The parameter should not vary greatly across the stock period because ADAM II replaces missing respondents with their nearest temporal neighbor. This replacement may not work perfectly, however, so the model allows the probability of selection to vary within a given stock period. Note that may be taken to be zero when k occurs during the flow period.^⁸

The term 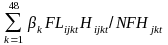appears in the model to account for variation in the sampling rate during the flow period. Because n_F is fixed while N_F varies, and because bookings are not evenly distributed over time, the probability of sample selection decreases with the number of bookings that occur during the half-hour when the arrestee is sampled. Hence NFH_jkt appears in the denominator. Given how the sample is selected, one would not expect to vary much over time, but allowing this parameter to vary by hour increases the model’s flexibility with little costs for the estimates.

The terms and appear in the model to account for variation in the sampling rate due to the severity of the charge. An arrestee booked during the stock period cannot be sampled if he is released prior to being approached by an interviewer. As mentioned before, the probability of being released during the stock period depends in part on the charge. One would not expect that the probability of being sampled varies appreciably across charge types during the flow period. 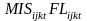However, it may be that arrestees charged with certain types of offenses (serious violent crimes) are comparatively inaccessible, so the terms and 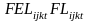are introduced. The interaction term 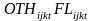is the reference category.

Finally, variations in the sampling probabilities across quarters are controlled for by adding quarter dummy variables for each year in the logistic model [1]. Table 1 (column 3) shows variability in the realized sampling proportions across periods. Without introducing these dummy variables into [1] (see column 4), the average estimated sampling probabilities fail to adequately capture the average realized sampling probabilities (compare columns 3 and 4). After introducing these dummy variables into [1] (see column 5), the average estimated sampling probabilities capture the average realized sampling probabilities (compare columns 3 and 5). Unless these seasonal differences are controlled, it may be impossible to model arrestees’ sampling probabilities correctly.

Table 1: Sampling Proportions By Quarter and Year
Year	Quarter	Realized Sampling Proportion (SP)	Estimated SP (Quarters not controlled)	Estimated SP (Quarters controlled)
2000	1	.137	.165	.137
2000	2	.149	.176	.149
2000	3	.209	.171	.209
2000	4	.216	.174	.216
2001	1	.150	.158	.151
2001	2	.152	.170	.153
2001	3	.191	.179	.192
Notes: Quarter 4 is missing in 2001 since ADAM interviews were not conducted in Portland in this quarter.

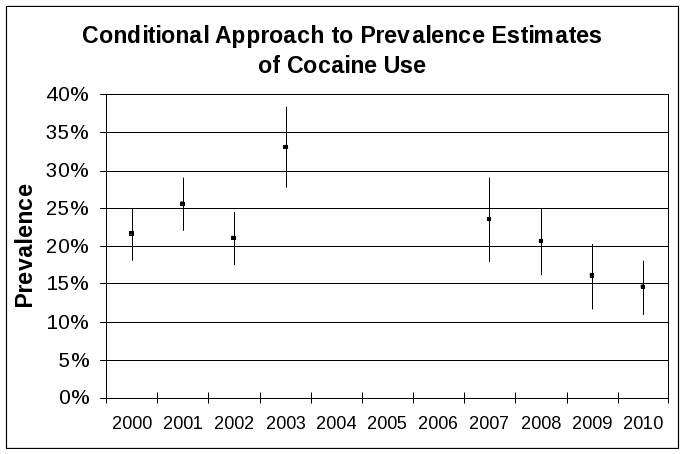
Figure 4 (panel a) shows the number of bookings and the number of arrestees in the sample by half-hour period; Figure 4 (panel b) reports the sampling proportions by half-hour period. The figures show some differences in the sampling rates between the stock period (roughly 20/100 were sampled) and flow period (roughly 15/100 were sampled). Because these sampling rates imply weights of 5 and 6.7, respectively, the conclusion is that the sample is reasonably balanced.

Looking at Figure 4 (panel b), there is apparent variation in the sampling rates from half-hour to half-hour. To prevent the weights from getting too large, the weights are trimmed so that the largest 5 percent of the weights have the same value, namely, the size of the smallest weight among the largest 5 percent. In Figure 4 (panel b), this places a ceiling of about 10 on these weights. The smallest weight is about 3. Again, the sample is reasonably balanced in the sense that there are no wide disparities in the weights.

Table 2 shows the number of bookings and the number of arrestees in the sample by charge. Overall the sampling probabilities do not vary materially with the charge. They are 0.18 for felony charges, 0.19 for misdemeanor charges, and 0.15 for other charges. Both the figures and table demonstrate that ADAM II is able to achieve reasonable balance with respect to booking time and charge, the two variables that are likely to have the greatest effect on sampling rates.

Figure 4

Panel a: Number of Bookings and Number of Sampled Arrestees by Half-Hour

Panel b: Sampling Proportions by Half-Hour

Table 2: Number of Bookings and Number of Arrestees In the Sample By Charge Portland 2000 and 2001
Charge	Number of Bookings	Number of Arrestees in the Sample	Sampling Rate
Felony	2492	456	0.18
Misdemeanor	2141	400	0.19
Other	2663	388	0.15

Table 3 presents coefficient estimates of the logit model specified by equation [1]. As would be expected, the parameter estimates are typically significantly different from zero. Although a reader cannot tell from inspection of the table (because estimated parameter covariance are not reported), the parameters do not necessarily differ from each other.

The model specification varies slightly across the sites due to variations in data availability, but departures from this generic form are never large. Variations are not detailed in this report, but as noted in the introduction, details are available in electronic form by request.

Table 3: Parameter Estimates from the Logit Model for Propensity Scores: Portland 2000 and 2001
Covariates	Coefficient	Std. Error	Z	P>\|z\|
Felony*Stock	-0.675	0.192	-3.52	0.000
Felony*Flow	-0.890	0.202	-4.41	0.000
Misdemeanor*Stock	0.193	0.114	1.70	0.089
Misdemeanor*Flow	-1.036	0.196	-5.28	0.000
Other*Stock	-0.136	0.116	-1.17	0.240
Stock*Half_Hour 1/NS_j	43.585	13.005	3.35	0.001
Stock*Half_Hour 2/NS_j	26.344	11.681	2.26	0.024
Stock*Half_Hour 3/NS_j	27.307	9.290	2.94	0.003
Stock*Half_Hour 4/NS_j	17.385	9.891	1.76	0.079
Stock*Half_Hour 5/NS_j	27.546	9.308	2.96	0.003
Stock*Half_Hour 6/NS_j	5.876	12.050	0.49	0.626
Stock*Half_Hour 7/NS_j	42.028	10.230	4.11	0.000
Stock*Half_Hour 8/NS_j	18.372	12.879	1.43	0.154
Stock*Half_Hour 9/NS_j	26.061	8.648	3.01	0.003
Stock*Half_Hour 10/NS_j	26.835	9.227	2.91	0.004
Stock*Half_Hour 11/NS_j	15.628	12.725	1.23	0.219
Stock*Half_Hour 12/NS_j	21.247	12.495	1.70	0.089
Stock*Half_Hour 13/NS_j	41.062	12.674	3.24	0.001
Stock*Half_Hour 14/NS_j	40.899	14.811	2.76	0.006
Stock*Half_Hour 15/NS_j	31.188	19.377	1.61	0.108
Stock*Half_Hour 16/NS_j	-12.757	18.706	-0.68	0.495
Stock*Half_Hour 17/NS_j	35.026	15.282	2.29	0.022
Stock*Half_Hour 18/NS_j	22.691	14.733	1.54	0.124
Stock*Half_Hour 19/NS_j	46.892	11.299	4.15	0.000
Stock*Half_Hour 20/NS_j	23.556	11.386	2.07	0.039
Stock*Half_Hour 21/NS_j	17.823	11.596	1.54	0.124
Stock*Half_Hour 22/NS_j	17.740	10.110	1.75	0.079
Stock*Half_Hour 23/NS_j	27.260	10.426	2.61	0.009
Stock*Half_Hour 24/NS_j	19.201	11.099	1.73	0.084
Stock*Half_Hour 25/NS_j	24.344	10.729	2.27	0.023
Stock*Half_Hour 26/NS_j	36.517	10.315	3.54	0.000
Stock*Half_Hour 27/NS_j	27.684	10.536	2.63	0.009
Stock*Half_Hour 28/NS_j	32.131	10.407	3.09	0.002
Stock*Half_Hour 29/NS_j	21.347	9.837	2.17	0.030
Stock*Half_Hour 30/NS_j	29.673	10.244	2.90	0.004
Stock*Half_Hour 31/NS_j	43.304	17.492	2.48	0.013
Stock*Half_Hour 32/NS_j	34.297	19.029	1.80	0.071
Stock*Half_Hour 33/NS_j	45.035	15.906	2.83	0.005
Stock*Half_Hour 34/NS_j	43.197	15.183	2.85	0.004
Stock*Half_Hour 47/NS_j	-47.981	30.179	-1.59	0.112
Stock*Half_Hour 48/NS_j	23.942	11.696	2.05	0.041
Flow*Half_Hour 1/NFH_jk	0.813	0.575	1.41	0.158
Flow*Half_Hour 2/NFH_jk	-1.618	1.169	-1.38	0.166
Flow*Half_Hour 31/NFH_jk	0.461	0.421	1.09	0.274
Flow*Half_Hour 32/NFH_jk	0.439	0.404	1.09	0.277
Flow*Half_Hour 33/NFH_jk	0.840	0.370	2.27	0.023
Flow*Half_Hour 34/NFH_jk	0.759	0.398	1.91	0.057
Flow*Half_Hour 35/ NFH_jk	1.493	0.367	4.07	0.000
Flow*Half_Hour 36/NFH_jk	0.332	0.374	0.89	0.375
Flow*Half_Hour 37/NFH_jk	0.283	0.388	0.73	0.466
Flow*Half_Hour 38/NFH_jk	0.763	0.347	2.20	0.028
Flow*Half_Hour 39/NFH_jk	1.263	0.335	3.77	0.000
Flow*Half_Hour 40/NFH_jk	0.027	0.393	0.07	0.946
Flow*Half_Hour 41/NFH_jk	0.936	0.328	2.85	0.004
Flow*Half_Hour 42/NFH_jk	0.886	0.335	2.65	0.008
Flow*Half_Hour 43/NFH_jk	0.965	0.334	2.89	0.004
Flow*Half_Hour 44/NFH_jk	0.024	0.392	0.06	0.952
Flow*Half_Hour 45/NFH_jk	-0.123	0.405	-0.30	0.762
Flow*Half_Hour 46/NFH_jk	-1.950	0.666	-2.93	0.003
Flow*Half_Hour 47/NFH_jk	-0.793	0.672	-1.18	0.238
Flow*Half_Hour 48/NFH_jk	1.600	0.548	2.92	0.004
Quarter 1 in 2000	-0.544	0.137	-3.97	0.000
Quarter 2 in 2000	-0.507	0.123	-4.13	0.000
Quarter 4 in 2000	0.023	0.116	0.20	0.843
Quarter 1 in 2001	-0.316	0.117	-2.70	0.007
Quarter 2 in 2001	-0.396	0.118	-3.36	0.001
Quarter 3 in 2001	-0.172	0.117	-1.47	0.142
Constant	-1.289	0.136	-9.46	0.000
Notes: In this table, Half_Hour_k denotes the dummy variable for half hour k. NS_j, and NFH_jk are defined as in the text. Quarter 4 in 2001 and other (drug offenses in Portland)*flow are the omitted dummy variables.

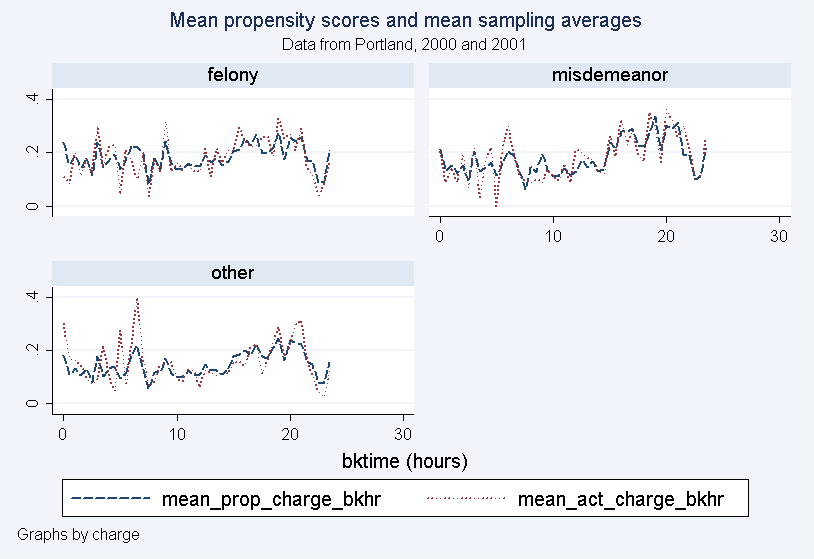
The estimated coefficients are then employed to predict propensity scores for the sampled arrestees. Inverses of the estimated propensity scores are the sampling weights. Figure 5 tabulates the mean propensity score estimates and the mean sampling averages as a function of the time of day and the charge. The largest discrepancy between the propensity score and the achieved sampling rate is for those times of the day when bookings are fewest (see Figure 4), but overall the figure suggests that the logistic model is successful in capturing the variation in the sampling rates by time of the day and charge.

Figure 5: Mean Propensity Scores and Mean Sampling Averages by Charge and Half-Hour

The new propensity score ADAM II weights and old ADAM weights are comparable in the sense that they both sum to the population size, but beyond that there are differences. The propensity score weights have a standard deviation of 2.89; the original ADAM weights have a standard deviation of 3.90. This suggests that the estimates based on the propensity score weights should have smaller sampling variances, because small variation in the weights should lead to smaller variances in the weighted estimates. In short, the ADAM II estimates are more precise than the original ADAM estimates. This additional precision improves both point estimates and trend estimates.

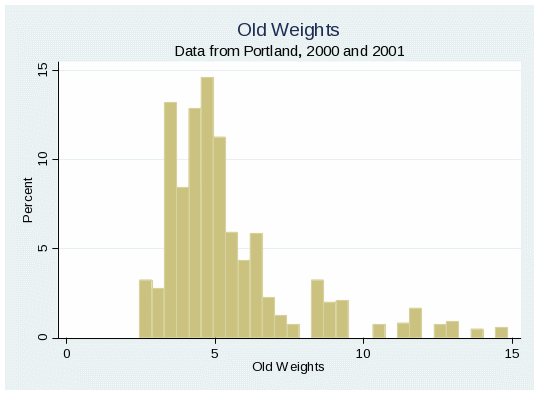
Figure 6 displays histograms of the propensity score weights and the old weights after discarding weights larger than 15 (which represents fewer than 1% of the propensity score weights and fewer than 3% of the old weights). These weights are discarded to improve the resolution of the figure. A regression of the propensity score weights on the old weights produce a regression:

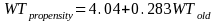
The parameter estimates are significant at P<0.001. The R²=0.09.

Obviously, the propensity score weights are not the same as the old ADAM weights. In part, this is because the old weights fall into discrete categories since they are based on a finite number of strata (Hunt and Rhodes, 2001). The new weights are comparatively continuous. Consequently, the old weights do not perfectly explain the new weights.

The propensity score weights are also not simply distributed about the old weights because the constant is 4.04 rather than 0. This finding seems curious, but the explanation is likely that the range of the weights is small. The average weight is about 5.9. The standard error about the regression is about 2.1. Thus, the propensity score weights are not actually much smaller or much larger than the original weights.

Figure 6: Propensity Score Weights and Old Weights

Estimating Propensity Scores for 2007 and Later Years

Formula [1] pertains to estimating propensity scores using data from Portland for 2000 and 2001.^⁹ The model described by formula [1] applies to 2007-2012 with model modification. Referring to formula [1], the last term is:

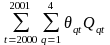
To extend the formula to 2007 and beyond, this term is replaced with:

Y_t is a dummy variable coded 1 if the arrestee was booked during the year t.

2012 represents the most recent year of ADAM II data. Note that beginning in 2012, since there is only one three week collection period per year, there is only one parameter estimated per year.

This formulation implies the update of propensity scores for each site every time that ADAM II is administered. Potentially, then, earlier ADAM estimates could be changed with each administration of ADAM II. This periodic updating was felt to be confusing, and it was decided to “freeze” estimates once reported. This decision has effects for estimates going forward, which are discussed in section 5.

Prior to 2011, the propensity score was updated every year using data from the original ADAM and ADAM II. Concerned that as booking practices change, the propensity score model would become mis-specified, the analysis team made a minor change to the estimation algorithm that was effective in 2011. . To overcome the potential problem changing practices pose, the methodology updated the propensity score model using ADAM II data exclusively starting in 2001. No weights or estimates were changed retrospectively for 2010 and earlier. All changes are prospective, affecting weights and estimates for 2011 and later.

Imputation of Missing Test Data

For a variety of reasons, some of the ADAM II sites have higher than expected levels of missing urine test results. The consequences of high missing urine rates and how they are dealt with are discussed here.

Dealing with Missing Test Data

Missing data are a frequent problem in social science research. Perhaps the most common way of dealing with missing data is to discard cases in which data are missing and only work with data that are not missing. The original ADAM project took this approach. Whatever the merits of this approach generally, discarding survey data when the urine test result is missing is problematic when missing data comprise a material proportion of the sample. First, there is the prospect of introducing bias, because those arrestees who fail to provide a urine specimen may differ systematically from those who provide a urine specimen, and the propensity score may fail to control for those differences. Second, when missing data are material, sampling variances will be larger than is intended by the planned sampling design.

Statisticians have developed sophisticated approaches for dealing with missing data problems (Rubin, 1987; Schaefer, 1997). While the ADAM II team explored some complicated approaches, ADAM II estimation relies on an approach that is simple. To provide some intuition for the approach, an imputation example is presented here for recent cocaine use. The ADAM II interview asks all respondents the question: Did you use cocaine within the last three days? The answer is either “yes” or “no.” In subset A of those respondents, ADAM II also obtains a drug test result, which indicates that the offender is either positive or negative for cocaine use in the prior three days. For subset B, ADAM II fails to obtain a test result, and imputations are done exclusively for subset B.

Using data from subset A, the probability of a positive urine test is P₁ when the respondent says that he used cocaine in the last three days, and the probability of a positive urine test is P₂ when the respondents says that he did not use cocaine in the last three days. P₁ is typically close to 1; P₂ is larger than 0 but much lower than 1 because (1) many respondents who deny use are being truthful so P₂ < 1, but (2) many respondents who deny recent drug use are being untruthful, so P₂ > 0. Turning to imputations for subset B, the best estimate is that a proportion P₁ of those offenders who answered “yes” to the 3-day question would in fact have tested positive for cocaine had they in fact been tested, and the best estimate is that a proportion P₂ of those offenders who answered “no” to the 3-day question would have tested positive for cocaine had they in fact been tested. Nothing in the approach assumes truthful reporting. This logic provides the basis for data imputation, although in practice (discussed below) the statistical underpinnings of this approach are complicated.^¹⁰

Deriving an imputation uses the following steps. First, the probability that a urine test result would be positive when an arrestee said that he had used a drug during the last three days is estimated. In fact, the probability is close to 1. Second, the probability that a urine test result would be positive when an arrestee said that he had not used a drug during the last three days is estimated. In fact, the probability is positive, but much closer to 0. Basically, the approach is to estimate these probabilities, draw a random sample from a Bernoulli distribution, and thereby assign a value of 1 or 0 to replace the missing value.

Although the basics of the imputation are simple, using the imputation when estimating the proportion of arrestees who tested positive for each drug is more complicated. Although a value of 1 or 0 based on the above procedure can be imputed, subsequent statistical analysis would not reflect two forms of sampling error without additional steps. First, the estimates of the probability of testing positive conditional on a self-report of recent drug use are, in fact, an estimate with its own sampling variance. Second, the random draw from the Bernoulli distribution is only one possible realization of a random process. Estimation must take additional sampling variation into account. A step-by-step explanation is provided below. These steps are taken separately for each site and for each drug.

1. According to current analysis, the probability of testing positive conditional on admission of use in the last three days does not vary much over time. Consequently, estimation is based on a simple model. Conditional on the respondent saying “YES” to the three day use question, the estimated probability of testing positive when the urine test is known is estimated as P₁. Conditional on the respondent saying “NO,” the estimate is P₂.

2. Of course P₁ and P₂ are estimates, but the distribution of the estimates is known—they are asymptotically normal with estimated variances of σ₁=P₁(1-P₁)/N₁ and σ₂=P₂(1-P₂)/N₂ respectively, where N₁ and N₂ are the number of observations with self-reports of “YES” and “NO” that have corresponding urine test results.

3. The distributions of σ₁ and σ₁ are distributed as inverted Chi-square with N₁ and N₂ degrees of freedom, respectively. Using a Bayesian logic (Lancaster, 2004), a realization of σ₁ and σ_{1 a} is drawn from the inverted Chi-square. These realizations are used in the next step.^¹¹

3. Continuing to apply Bayesian logic, estimates of P₁ and P₂ are drawn from the normal distribution conditional on the previous draws of σ₁ and σ₂.

4. The previous draws of σ₁ and σ₁ and of P₁ and P₂ define two independent normal distributions.

A. Conditional on an offender saying that he used the drug in the last three days, random draws are made from the normal with P₁ and σ₁. Missing responses for urine test results are replaced with these random draws. No non-missing reports for urine test results are replaced.

B. Conditional on an offender saying that he did not use the drug in the last three days, random draws are made from the normal with P₂ and σ₂. Missing responses for urine test results are replaced with these random draws. No non-missing reports for urine test results are replaced.

5. Steps 2 through 4 are repeated twenty times. Schaefer (1997) argues that five to ten repetitions are usually adequate for computing standard errors, but computing time is insignificant for the ADAM II problem, so the computing algorithm uses a conservative twenty repetitions. (Testing shows that more repetitions [50] are unnecessary because results do not change.) This leads to twenty data sets that have the same responses when the urine test result is known and potentially different imputed responses when the urine test result is otherwise missing.

6. Each of these data sets yields parameter estimates and a variance.

A. These estimates are averaged to produce the grand estimate. This is reported as the estimate.

B. Twenty variance estimates are computed for each of the 20 point estimates. These are averaged to produce a grand estimate of the variance. Call this V1.

C. The variance of the 20 point estimates is computed. Call this V2.

D. The variance estimates used for reporting is V=V1+V2. The square-root of V is reported as the standard error.

One might improve the imputation by using multiple imputation procedures—for example, by adding age, race and other variables to the imputation model. Although this improvement is possible, the imputations are applied in computing loops across drugs and over sites, and simplicity is desirable.^¹²

Special case of Washington, DC

What follows is the step-by-step estimation procedure used for Washington, D.C., for ADAM II data from 2000 - 2011:

1. Given the availability of PTS data, the DC census data are divided into two partitions: arrestees whose urine tests are reported by PTS data and arrestees whose urine tests are not reported by PTS data. The estimation methodology differs for these two partitions.

a. The first partition comprises all arrestees who are represented in the PTS data. Establishing this partition is judgmental, based on an inspection of the offense types that appear in the PTS data and the offense types that appear in the census data.

b. The second partition comprises all arrestees who are not represented in the PTS data.

c. A total of N1 census records have a corresponding record in the PTS data. A total of N2 census records have no corresponding record in the PTS data.

2. The proportion of adult males who test positive for a month according to the PTS data is computed as P1.

3. Otherwise the probability of testing positive during the sampling period is P2. It has a sampling variance of S2. P2 and S2 are estimated exactly the same way that drug test results are estimated in every other ADAM II sites.

4. The grand estimate of the probability of testing positive in DC is:

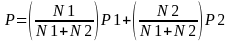
The sampling variance is:

This explains the estimation procedure for Washington, D.C. P is an estimate of the proportion of arrestees who test positive for a specified drug. P1 comes from analysis of the PTS data and P2 comes from analysis of the ADAM II data that do not have corresponding records in the PTS data. The two are weighted by the proportion of census records that do and do not have corresponding PTS records.

VAR is the sampling variance. There is no variance when the estimate is based on the PTS data because the sample equals the population. The only component of the variance comes from the ADAM II records that are used in the estimation of P2.

Beginning in 2012, only the Washington, D.C. booking data and PTS data were available. Therefore, we may only estimate P1, the proportion of adult males who test positive for a month according to the PTS data. To preserve compatibility with the ADAM II data, we weighted individual urine tests to the booking data, using the propensity weighting strategy described in equation [1]. For the PTS data, we used a different specification for , as it was unnecessary to control for the sampling proportions within stock and flow periods:

Developing Estimates

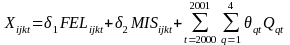
ADAM II reports two types of estimates. One is a point prevalence estimate such as the proportion of arrestees who test positive for cocaine. The second is trend estimate that reflect the short-run and long-run changes in drug use.

Point Prevalence

As the term is used here, a “point prevalence” estimate is an estimate of the proportion of arrestees who would have tested positive for a specific drug had all arrestees been tested for that drug during the 21-day period when ADAM II sampled arrestees in 2012. Three methods for calculating the point-prevalence estimate of the proportion of arrestees testing positive for methamphetamine were first developed using data from Portland as a prototype. The methods were then extended to all sites and each of the drugs of interest.

The first method uses an unweighted logit regression to model the probability of a sampled arrestee’s testing positive for a particular drug. This regression uses the results from urine testing as the dependent variable and variables that appear in the census data as independent variables. These independent variables will be described subsequently. Then, estimation uses the coefficient estimates from this model to estimate the probability of testing positive for every arrestee appearing in the census data. (The prediction applies to arrestees for whom there are no drug test results. The drug test results, rather than the predictions, are used otherwise.) Finally, these predicted probabilities are averaged over the population of all arrestees to compute the point-prevalence estimate.

The second method is very similar to the first one, except it employs inverses of the propensity scores as weights when estimating the logit model for testing positive for a particular drug. The second method is used in developing trends over time.

Lastly, using the inverses of the propensity scores, the third method estimates the weighted proportion of arrestees who tested positive for a drug in the survey sample.^¹³ Since the weights are an important element in the analysis, the third method is used for estimating point prevalence.

These three approaches are asymptotically equivalent, provided models are correctly specified. That is, the first two approaches will produce estimates that are consistent, provided the regression of urine test results on census variables is correctly specified. The second and third approaches will produce estimates that are consistent, provided the propensity score regression is correctly specified. All three estimates will be consistent, if both the propensity score regression and the urine testing regression are correctly specified.

This report previously explained the estimation of the propensity scores. To explain the first two estimators identified above, logistic regression is used to regress the outcome from a drug test onto variables that appear in the census data. The illustration comes is based on Portland ADAM data for 2000 and 2001, which was historically the first test site. However, the exercise has been repeated in each of the other sites and similar results were obtained in all.

When regressing the test results onto the census variables, let index i denote an arrestee booked on the j^th day of year t. In addition, let N_jt be the number of bookings occurred on the j^th day of year t and n_jt be the number of arrestees selected into the sample on day j. The data are arranged in such a way that for the j^th day of year t, the index i runs from 1 to n_jt for members of the sample and it runs from 1 to N_jtfor members of the population, where N_jt> n_jt. Using these indexes, the following variables are defined:

M_ijt This is a dummy variable coded one if the ith arrestee, who was booked and sampled on the j^thday of year t tested positive for methamphetamine. It is coded zero if he tested negative. Note that this variable is available for . It is unobservable, and therefore missing for .

P (M_ijt=1) This is the probability that the ith arrestee booked on day j tested positive for methamphetamine. It is estimated from available data.

FV_ijt This is a dummy variable coded one if the ith arrestee booked on day j was charged with a violent felony and coded zero otherwise.

FP_ijt This is a dummy variable coded one if the ith arrestee booked on day j was charged with a property felony and coded zero otherwise.

FO_ijt This is a dummy variable coded one if the ith arrestee booked on day j was charged with a felony that cannot be categorized as a violent, property related or drugs related offense and coded zero otherwise.

MV_ijt This is a dummy variable coded one if the ith arrestee booked on day j was charged with a violent misdemeanor and coded zero otherwise.

MP_ijt This is a dummy variable coded one if the ith arrestee booked on day j was charged with a property misdemeanor and coded zero otherwise.

MO_ijt This is a dummy variable coded one if the ith arrestee booked on day j was charged with a misdemeanor that cannot be categorized as a violent, property related or drugs related offense and coded zero otherwise.

YD_tThis is a dummy variable coded one for the observations from 2000 (t=2000) and zero otherwise.

Using the sample data ( ), estimate the following logistic regression:

where Z_ijt is defined as:

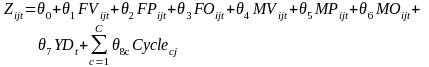
Note that this model specification captures any differences of drug use across charge categories defined by the severity (felony, misdemeanor, other) and the nature (violent, property, other) of the charge. A dummy variable that estimates the yearly trend in the overall drug use between years is included. Finally, the last term in [2], which is based on Fourier transformations, represents half-yearly and yearly cycles, which control for periodicity in drug use.

This logistic model is estimated first without using any weights; this is the basis for the first estimation method. Then the logistic regression is estimated using propensity score weights. This is the basis for the second regression. Coefficient estimates and standard errors are displayed in Table 4. As would be expected given that the sample is balanced, the parameter estimates are similar for the weighted and unweighted regressions.

Estimates reported for ADAM II use the ADAM data for 2000-2003, as well as the ADAM II data. Additional year dummy variables control for the year and provide the means to test for trends.^¹⁴ Table 4 is just an illustration of the approach.

Table 4: Determinants of Methamphetamine Use in Portland: Weighted and Unweighted Logistic Regression
	Unweighted Logistic		Weighted Logistic
Covariates	Coefficient	Std. Error	Coefficient	Std. Error
Felony-Violent	-0.269	0.231	-0.258	0.218
Felony-Property	0.293	0.236	0.233	0.217
Felony-Other	-0.033	0.199	-0.046	0.177
Misdemeanor-Violent	-1.038***	0.254	-0.941***	0.247
Misdemeanor-Property	-0.829***	0.28	-0.836***	0.279
Misdemeanor-Other	-0.728**	0.35	-0.848***	0.316
Sin Year	-0.075	0.131	-0.199	0.125
Cos Year	-0.037	0.11	-0.02	0.109
Sin Half-Year	-0.174	0.313	-0.48	0.319
Cos Half-Year	0.061	0.379	0.363	0.392
Year 2000	-0.059	0.182	-0.071	0.170
Constant	-0.952***	0.152	-0.84***	0.140
N	1242
Notes: * p<0.01, p<0.05, * p<0.1.

In order to test the significance of the estimated coefficients of the charge categories and the cycle covariates, the Abt team performed likelihood ratio and Wald tests for the unweighted and weighted specifications respectively.^¹⁵ Results of these tests suggest that the coefficients on the charge categories are jointly significant, whereas the coefficients for the cycles are not significant at conventional levels.^¹⁶ At least for Portland during the period studied, it appears important to take offense category into account, but unimportant to take seasonality into account. These findings can change as ADAM II data are added to the study and when the regressions are applied to other sites. Most importantly, the analysis shows how offense and seasonality are taken into account without prejudging if offense and seasonality must be taken into account by the analysis. The electronic documentation for specifics across each of the sites is available by request.

These results emphasize why weighting is important for estimation. Each of the misdemeanor categories predicts a lower rate of testing positive than does the omitted drug category. (The felony categories do not differ significantly from the omitted drug category). Consequently, in this example, unweighted statistics would produce biased estimates of methamphetamine use, if the sampling probabilities differed by felony and misdemeanor charges. As noted previously, the sampling probabilities do vary by charge category during the stock and flow periods. Hence, failing to weight is a potential problem for estimation.

It may not be a large problem, however. The ADAM II sample is reasonably balanced, meaning that the sampling probabilities are roughly constant for all members of the sample. If the sampling probabilities were exactly equal, there would be no need to weight. The fact that they are close to equal implies that unweighted estimates will not depart greatly from weighted estimates. However, one cannot be sure that this balance will be maintained as additional data are assembled over time; nor is it certain that this high level of balance will be preserved across the ADAM II sites. .

The first two estimation methods use the coefficient estimates reported in Table 4. The third uses only the propensity score weights. Results using each method are presented and compared below.

Method 1

Method 1 uses results from the unweighted logistic regression [2] to estimate in this example the proportion of arrestees who would have tested positive for methamphetamine had all arrestee been tested. Using these coefficient estimates, the probability of testing positive for methamphetamine is estimated for every member of the population. Call this:

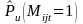
where the subscript u shows that this is the unweighted probability estimate. Using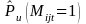 , the point prevalence value (proportion of arrestees testing positive) is estimated by:

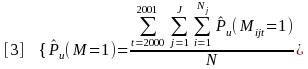
where N denotes the number of arrestees in the census and J represents the number of days in the sample. (i.e.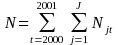 ). The standard error of this proportion is derived using a standard Taylor approximation. Let 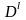be the derivative of P_u(M_ij=1) with respect to the l^th parameter in the logistic model in [2]:

Note that here, X^l denotes the l^th covariate in the model. There are L of these D^l terms (l=1, 2,…, L) so that D is defined as the Lx1 column vector:

Let 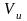denote the variance-covariance matrix for the parameters from the unweighted logistic regression. Then the sampling standard error for the proportion P (M=1) is calculated by:

where D^T is the transpose of D. For example, using this approach, the unweighted point-prevalence estimate of the proportion of arrestees testing positive for methamphetamine is 0.221 with a standard error of 0.012.

Method 2

The second method for calculating the point-prevalence estimate also employs the logistic model represented by equation [2]. Here, the only difference is that inverses of the propensity score estimates from equation [1] are used as weights when estimating this logistic regression. Resulting parameter estimates and standard errors are presented in Table 4. Note that here, when estimating the standard errors, estimation takes into account the fact that the propensity scores have been estimated. Otherwise the second and first estimation procedures are the same. Utilizing this second method, the point-prevalence estimate is 0.226 with a standard error of 0.011 for methamphetamine. The extensions to other drugs for this site are found in Tables 5 and 6 in the Appendix.

Method 3

The third method for the point-prevalence estimate uses the inverses of the propensity scores to weight the arrestees who tested positive for methamphetamine. Let:

PS(U_ijt=1) This is the estimated propensity score of the i^th arrestee’s (booked on the j^th day of year t) providing a urine sample.

Then the point-prevalence estimate is calculated by:

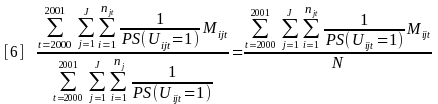
Recall that n_jt denotes the number of arrestees sampled on day j. Using this formula, the point-prevalence estimate is found to be 0.226 with a standard error of 0.013 for methamphetamine.^¹⁷

Discussion of the Three Methods

All three methods are consistent for the true rate of testing positive for methamphetamine provided the propensity score model and the drug test model are correctly specified. The three estimates are virtually indistinguishable. The three estimates can be compared with the estimate that results from using the previous ADAM weights and with unweighted estimates. For instance, when the previous ADAM weights are used in place of the propensity score weights in the second method, the point-prevalence estimate becomes 0.225 with a standard error of 0.012, which is very close to the previous three estimates. Finally, the unweighted proportion of sampled arrestees testing positive for methamphetamine is 0.220 with a standard error of 0.012. Given the balance in this sample, the unweighted estimates do not depart materially from the weighted ones.

Extending the Estimators to Other Drugs and Other Variables

The illustration has focused on a single drug (methamphetamine) in a single ADAM site (Portland) for each of three estimators. Table 5 and Table 6 (in the appendix) show comparable estimates for three other drugs (cocaine, heroin, and marijuana) for the same years in Portland.^¹⁸

As was true for methamphetamine in Portland, Table 6 shows that each of the three estimation procedures produces similar point estimates and standard errors. Method 2 is preferred, because the estimates are consistent, provided either equation [1] or [2] is correctly specified. Nevertheless, all three estimation procedures produce good estimates, and provided a user ignores the complicated variance calculations, method 3 is the easiest to apply. The cost of ignoring the complicated variance calculations is slightly inflated standard errors, but experience is that the inflation factor is small and acceptable.

When estimating prevalence using ADAM II data, the following rules apply:

When estimating the proportion of offenders testing positive for a drug of interest, typically the second method is used.
Some drugs have very low prevalence, and for them the third method is used. This approach is required because it is not possible to estimate equation [4] for rare outcomes.
For prevalence estimates other than the proportion of arrestees testing positive for drugs, the third method is used.

In practice, the methodology described by the first two bullets is slightly modified to deal with missing drug test results. This modification is described in subsection 4.1.

Extending the Estimators to Other Drugs and Other Variables

The example in formula [2] pertains to Portland for 2000 and 2001. Extending the estimator to other sites and other years is straightforward. Returning to formula [2], replace the term:

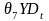
with the term:

This is an obvious extension. The YD are year dummy variables.

Formula [2] in both its original and modified forms pertains to urine test results. For some purposes, it is useful to modify the estimation procedure and extend it to other variables including self-reports, offender characteristics, and so on. Specifically, a modification of [2] provides:

Here Y_ijt is a generic outcome variable, F(…) represents some appropriate link function, and Z_ijt is defined as:

This model only uses quarters and years. The more complicated model (with offenses and Fourier transformations) is used for all estimates based exclusively on the urine tests. The simpler model (with just the year and quarter) is used to annualize all statistics that involved self-reports in any form.^¹⁹ The process of annualizing the statistics is discussed in the next section.

Trends and Annualizing the Statistics

The logistic regression model estimates the probability of testing positive for a specified drug conditional on the offense, season, and the year. This regression can be extended to all years of data using the propensity score weights for 2000 and 2001, the original ADAM II weights for 2002/2003, and the propensity score weights for later years (2007-2012). The year parameter is especially useful for testing the null hypothesis that drug use has not changed between any two years (i.e., 2000-2001, 2002-2003, 2003 and 2007, etc.) or between any clusters of years (i.e., 2000 through 2003 and 2007 through 2012).

In order to represent how drug use changes over the years, the point-prevalence estimates of drug use are calculated for each year of interest using two approaches. The unconditional approach calculates the point-prevalence estimates for each year using the second method as described above. Using Portland data as the example, Figure 7 plots the point prevalence estimate for each year and provides a 95 percent confidence interval about the point estimates. In the conditional approach, the estimated regression equation [2] is evaluated at the mean values of the independent variables (setting the cycle values to zero) for each year. Figure 8 plots the corresponding conditional point prevalence estimate and provides a 95 percent confidence interval. Because Figures 7 and 8 are sufficient to demonstrate the concepts involved; we have not updated them using 2011 and 2012 data.

The first (Figure 7) and second (Figure 8) methods of estimating trends differ both conceptually and numerically. If arrest practices change over time, so that, for example, a larger proportion of arrestees are booked for drug-law violations, then the unconditional estimate will differ from the conditional estimate because the conditional estimates hold arrest practices constant and annualize the estimates. The conditional estimate is a better reflection of trends in drug use because arrest practices are partly a political decision. For example, a jurisdiction’s decision to place renewed emphasis on making arrests for public order offenses (as occurred in Manhattan during the ADAM era) would change the distribution of charges in the booking population and the positive drug test rates without there really being a change in drug use. Another example is a political or legal change in pretrial detention practices, for example, by expanding the use of field citations.

Estimating the probability of testing positive at a fixed mix of charges controls for these political and administrative changes. Furthermore, when there are annual cycles in drug use, the unconditional estimate is sensitive to when the survey was actually conducted. The conditional estimate, in contrast, can be seen as annualized because it sets the cyclical variables to their mean values for the year (namely, zero). When the regression includes quarters instead of Fourier transformations, the estimates are annualized by setting the estimates equal to the average over the quarters.

Figure 7: Trends in Cocaine Use Based on the Unconditional Approach

Figure 8: Trends in Cocaine Use Based on the Conditional Approach

However, a change in drug use may itself result in changes in the booking populations; this would happen, for example, if increased drug use caused more drug-law violators to come to the attention of police. On balance, political and legal decisions are of greater concern, but for public policy purposes, it seems worthwhile to report trends based on both measures.

It is important to know if there was a statistically significant change in drug use between any two years. One cannot answer this question by inspecting Figure 7 or Figure 8, because the estimates are not independent, so the simple overlap of the confidence intervals is not a reliable guide to whether two estimates differ. However, the differences between any two years (such as 2003 and 2007) or clusters of years (such as 2000/2001 and 2002/2003) can be tested using the estimated covariance matrix from the logistic regression. When figures comparable to Figures 7 and 8 appear in the ADAM II annual reports, the report indicates when the estimates for two sequential years are statistically significant.

Confidence Intervals for Trend Analysis

Because the trend estimates are based on a regression model that uses all the data from across the ADAM and ADAM II years (both data weighted with propensity scores and data weighted with the original ADAM method), the parameter estimates for the yearly trends are not independent, a fact that complicates the development of confidence intervals.

Let V represent the parameter covariance matrix for the year dummy variables in the logistic regression with dependent variable “testing positive for drug D”. If there were four years of data, the covariance matrix would be a symmetric 4x4 matrix:

The terms in this matrix represent the variances and covariances for the four parameter estimates pertaining to year dummy variables, and one of the four year dummy variables is the omitted category. The terms below are not shown for below the diagonal, because the matrix is symmetric.

Let B represent a row vector with the parameter estimates for the four year dummy variables:

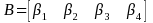
Let P represent a second row vector that records the average probability of testing positive for each of the four years.

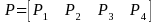
The difference between the parameter estimates for year i and year j has an approximately normal distribution with a sampling variance of:

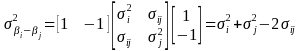
This sampling variance can be used to test the null hypothesis that the probability of testing positive for drug D has changed between year i and year j.

Confidence Intervals for Point Estimates

For ADAM II data, the delta method is used to estimate a confidence interval for a point estimate. This approach requires no new notation, because the discussion surrounding equations [3], [4] and [5] presented earlier already introduced suitable notation when explaining how to estimate the standard error for the confidence interval for testing positive for drug use. See equation [5].

The estimate of the confidence interval for the estimate of testing positive for drug use conditional on a fixed set of covariates is actually a simplification. First, in equation [3], the probability of testing positive during a year for the average arrestee is estimated. The average arrestee is a hypothetical arrestee who has an average value on all variables that enter into the logistic regression used to estimate the probability of testing positive for a specified drug, except that the year dummy variable is not averaged. Second, the estimate for each year is computed for the average arrestee, allowing only the year variable to change from year to year. This approach is a simplification compared with equations [3], [4] and [5] because calculations require no summations. All calculations are specific to the average offender.

Linear Trends

We also report a test for a linear time trend in the ADAM annual report. For this test we run a separate weighted regression similar to the model with offenses and Fourier transformations. The difference is that we replace all of the year dummy variables with a single variable, a time trend that ranges from 0 representing the earliest year to 1 representing the latest year. The null hypothesis is that the parameter associated with this time trend is zero, and we report the p-value from the test of that hypothesis.

Examining Figures 7 and 8, future trend analysis should consider non-linear trends. Presently data are sparse, so a linear trend seems justified and, of course, answers the question of whether there have been linear trends over this eleven year period.

Estimating Trends for 2008 and Beyond

From 2000 through 2003, ADAM used post stratification to estimate sampling probabilities and to calculate weights. Data were stratified by jail, stock and flow, and day of the week. Within each stratum, the sampling probability was estimated as the number sampled per number booked. Although conceptually simple, the approach was operationally difficult. The principal operational difficulty was that strata sometimes had no or few members of the sample. This meant that strata had to be merged, and it often resulted in heterogeneous strata being combined.

To avoid these complications, ADAM II adopted propensity scores as an alternative device for estimating sampling probabilities and computing weights. The propensity score approach does not require stratification, because the sampling probability can be modeled as a continuous function of factors that affect the sampling rate. As mentioned earlier, because 2000 and 2001 ADAM data provided the necessary census data, the survey team replaced the original weights for the 2000 and 2001 ADAM data with new weights based on propensity scores. That is, the survey team replicated the ADAM II weighting procedure using the 2000 and 2001 ADAM data.

This replication was not possible for the 2002 and 2003 ADAM data because the ADAM contractor for those years did not retain the census data for those years. Thus, for purposes of reporting trend statistics, the ADAM II survey team:

Uses the reweighted ADAM data for 2000 and 2001;
Uses the ADAM data for 2002 and 2003 without changing the weights; and
Uses the propensity score weights for the ADAM II data.

It is important to note that there was nothing wrong with the original ADAM weights. They simply led to sampling variances that were larger than necessary, so the ADAM II study team improved the weights when possible. Because there was nothing wrong with the original sampling weights, there is nothing misleading about mixing the reweighted data for 2000-2001, the 2002-2003 data with their original weights, and the new ADAM II data in producing trend estimates.

However, this reweighting has two consequences. The first is that the 2000- 2001 estimates changed slightly from those reported earlier. The second is that estimates from year-to-year in reweighted years are no longer independent. Consequently, to test for trends, an analyst requires an estimate of the parameter covariance matrix.

As anticipated, this has the result of potentially slightly changing the prior years’ estimates that appeared first in the 2007 report. Although this approach improves the efficiency of the estimates, there is concern that yearly revisions going forward, regardless how slight, would be confusing. Consequently, 2008-2012 estimates are developed holding earlier estimates at their previously reported levels.

In this procedure, the earlier estimates for parameters and standard errors are treated as fixed for subsequent estimation. There are five steps for estimation procedures for 2008 and beyond data.

The first step uses the regression results that are part of the 2007 report. Recall from equation [2] that these are a function of the offense, the Fourier transformations, and the year dummy variables. All the θ parameters and the covariance matrix are retained for those θ parameters V_θ. For convenience, equation [2] is repeated as equation [7].

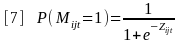
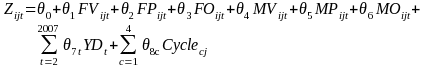
Following Bayesian logic, analysts sample the covariance matrix V_θ from an inverted Wishert distribution. Conditional on that sampled V_θ, analysts sample θ from a multivariate normal distribution.
Conditional on the θ in the previous step, a new regression is estimated with the specification described by equation [8]. Note that this regression has a single free parameter β.

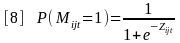
The β could be estimated using just one year of ADAM II data, but using the entire set of ADAM II data is a programming convenience.

Steps 3 and 4 are cycled through 100 iterations. Each iteration provides a somewhat different estimate of β (100 β estimates β₁ through β₁₀₀) and somewhat different estimates of (100 estimates through ). The final estimate of β and are:

[9]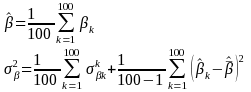

The above steps provide everything needed for trend estimation except the covariances between β and the θ_7t. To estimate the covariance estimates for β and any selected θ, the formula is:

[10]

Given estimates of the variance and covariance for the parameters associated with the year dummy variables, the statistical significance of any pair of years can be tested.

This approach is useful because it guarantees that once an estimate is reported for a year, it will not change as the ADAM II data are updated for subsequent years. There is a noteworthy disadvantage, however. The θ parameters do not get updated as new ADAM II data accumulate. A reader can object that the past data have an undue influence on current and future estimates.

In the future, consideration could be made to recalibrate the regressions so that past reports of prevalence are not held constant. For example, as of 2012, an analyst might recalculate prevalence estimates for 2000 through 2012. This would change past estimates slightly, and it may change them more than slightly if the θ parameters change over time. Revisions should check for the constancy of the θ parameters. Analysts could then fix the 2000 through 2011 estimates as data accumulate for 2013 and beyond.

Additionally, one might consider the relying on trend estimates beginning with 2007 as ADAM II collects data beyond 2012. This would allow a simplification because the control variables for cyclical patterns would be unnecessary. This follows because ADAM II always administers its surveys at approximately the same calendar time every year.

Annualizing Point Prevalence Estimates

Most of the statistics appearing in the ADAM II reports are point prevalence estimates. A point prevalence estimate is straightforward, because it only requires weighting the desired variable by the propensity score weights. The statistics reported in the 2007 ADAM II report and subsequent reports use this estimator, shown below in an illustration of the methodology.

As mentioned above, in preparation for the 2007 ADAM II report, it was determined that the prevalence estimates should be annualized to account for the fact that the ADAM sample was collected at different times during the year (3 or 4 quarters versus 2 quarters in ADAM II). This complicates the estimation explained in the previous subsection.

Annualizing the prevalence estimates requires applying the same five steps as above, except that equation [7] is replaced with equation [11]:

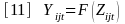
F(…) is a link function that depends on the context. When the variable of interest is binary, for example, F(…) represents the logit. Also Z is simplified:

The Q are dummy variables representing quarters of the year. The λ parameters are estimated using data from before 2008. The β parameter is estimated using 2008 data. The same procedure is followed in later years. The parameter covariance matrix is estimated by following steps 1 through 5 from the previous subsection.

When making the estimates, each Q is set equal to 0.25 and each year before 2008 is set equal to 0. This gives an annualized estimate of every variable reported in the 2008 and beyond for estimates exclusive of drug test results.

Special Issues

Special issues arise in different sites. To reweight the ADAM II data, the methodology requires consistent reporting of charge codes during 2000, 2001, 2007 and later. (Again, the 2002 or 2003 data cannot be reweighted because the census data for those years are lacking). Tabulations of specific charge codes over the years suggest that the offense categories were not always reported consistently. There appeared to be no problem with consistently identifying the four broad offense types (violent, property, drugs and other), but there were problems with distinguishing severity levels (felony, misdemeanor and “other”). Frequently misdemeanor and “other” categories have to be merged in analyses and sometimes it is necessary to ignore the severity categories altogether. As a result, the propensity scores may be based on fewer offense categories than are identified earlier in equation [1].

Concluding Comments

In summary, developing estimates for ADAM II poses several challenges.

In reviving ADAM in 2006, the program faced the challenge that ADAM had not been operational since 2003, and for some sites the layoff had been longer and collection sporadic. As seen during data collection beginning in 2007, many of the old ADAM sites had undergone changes. New jails had opened; some old jails had closed. Even when the jails remained the same, their use and purpose sometimes changed since the ADAM years Furthermore, law enforcement practices often change, so that the jail populations represented by the ADAM sample can differ from the jail populations represented by the ADAM II sample. Consequently, sampling and estimation procedures used in ADAM did not necessarily transfer directly into suitable procedures for ADAM II.

In addition, for reasons not yet fully understood, ADAM II respondents in two of the ADAM II sites (New York and Washington, D.C.) have been less willing than those in ADAM to provide urine samples. The resulting bias and inflated standard errors are of concern, so procedures for imputing values for missing drug test results are implemented in ADAM II. After experimentation, a simple provisional method was developed. However, every ADAM II site seems to pose a new challenge, and it is anticipated that this imputation methodology will change over time as the best way to analyze these data is found.

Both the Drug Use Forecasting system and the original ADAM provided yearly estimates of drug use. But neither DUF nor ADAM attempted to provide a probability basis for estimating trends. Estimating meaningful trends is deceptively difficult because of changes that have happened since 2000. As noted, jails and the populations they house have gone through changes; failing to account for those changes confuses trends attributable to changes in law enforcement and judicial practices with changes attributable to the frequency of drug use. The process of developing trend estimates is especially challenging because problems could not be identified and solutions explored until ADAM II data was collected and weighting undertaken. Given six years of ADAM II data, the Abt team continues to make modifications of estimation procedures and refine analyses.

References

Hirano, K., Imbens, G. and Rider, G. (2003) “Efficient estimation of average treatment effects using the estimated propensity score,” Econometica Vol 71 (4): 1161-189.

Hunt, D. and Rhodes, W. (2001) Methodology Guide for ADAM. National Institute of Justice, Washington DC.

Lancaster, T. (2004) An Introduction to Modern Bayesian Econometrics. Malden, MA. Blackwell Publishing.

Morgan, S. and Winship, C. (2007) Counterfactuals and Causal Inference: Methods and Principals for Social Research. Cambridge University Press.

Robins, J., and Rotnitzky, A. (1995) “Semiparametric efficiency in multivariate regression models with missing data,” Journal of the American Statistical Association Vol 90 (429): 122-129.

Rosenbaum, P. (1984) “From association to causation in observational studies: The role of tests of strongly ignorable treatment assignment,” Journal of the American Statistical Association Vol 79 (385): 41-48.

Rosenbaum, P. and Rubin, D (1984) “Reducing bias in observational studies using subclassification on the propensity score,” Journal of the American Statistical Association, Vol 79 (387): 516-524.

Rotnitzky, A. and Robins, J. (1995) “Semiparametric regression estimation in the presence of dependent censoring,” Biometrica Vol 82 (4): 805-820.

Rubin, D. (1987) Multiple Imputation for Nonresponse in Surveys. New York, John Wiley & Sons/

Schaefer, J. (1997) Analysis of Incomplete Multivariate Data, New York, Chapman and Hall.

Wooldridge, J (2003) Cluster sample methods in applied econometrics,” The American Economic Review Vol 93 (2): 133-138.

Appendix

Tables 5 and 6

Table 5: Determinants of Cocaine, Heroin and Marijuana Use in Portland: Weighted and Unweighted Logistic Regression
Drug	Cocaine		Heroin		Marijuana		Methamphetamine
	Unweighted	Weighted	Unweighted	Weighted	Unweighted	Weighted	Unweighted	Weighted
Covariates

Felony-Violent	-1.069***	-1.093***	-0.902***	-0.819**	0.195	0.269	-0.269	-0.258
	(0.25)	(0.21)	(0.32)	(0.27)	(0.20)	(0.17)	(0.231)	(0.218)
Felony-Property	-0.927***	-0.698**	-0.662**	-0.727**	0.130	0.243	0.293	0.233
	(0.28)	(0.27)	(0.33)	(0.30)	(0.22)	(0.20)	(0.236)	(0.217)
Felony-Other	-0.393**	-0.273	-0.354	-0.353	-0.0188	0.0287	-0.033	-0.046
	(0.19)	(0.17)	(0.24)	(0.22)	(0.18)	(0.16)	(0.199)	(0.177)
Misdemeanor-Violent	-1.179***	-1.118***	-1.842***	-1.964***	-0.110	-0.218	-1.038***	-0.941***
	(0.23)	(0.20)	(0.41)	(0.35)	(0.18)	(0.16)	(0.254)	(0.247)
Misdemeanor-Property	-0.444*	-0.422*	0.146	-0.0918	-0.169	-0.0527	-0.829***	-0.836***
	(0.23)	(0.20)	(0.25)	(0.23)	(0.21)	(0.19)	(0.28)	(0.279)
Misdemeanor-Other	-1.042***	-0.999***	-0.603	-0.698*	-0.908***	-0.780**	-0.728***	-0.848***
	(0.35)	(0.31)	(0.38)	(0.38)	(0.31)	(0.33)	(0.35)	(0.316)
Sin Year	-0.221*	-0.278**	-0.0952	-0.103	0.0617	0.0170	-0.075	-0.199
	(0.13)	(0.11)	(0.16)	(0.13)	(0.11)	(0.101)	(0.131)	(0.125)
Cos Year	0.0547	0.0924	-0.0928	-0.0517	0.0234	0.0253	-0.037	-0.02
	(0.10)	(0.10)	(0.13)	(0.12)	(0.093)	(0.085)	(0.11)	(0.109)
Sin Half-Year	0.174	0.119	-0.0759	-0.227	0.244	0.218	-0.174	-0.48
	(0.31)	(0.28)	(0.38)	(0.33)	(0.27)	(0.249)	(0.313)	(0.319)
Cos Half-Year	-0.224	-0.116	0.0545	0.183	-0.236	-0.244	0.061	0.363
	(0.37)	(0.34)	(0.46)	(0.41)	(0.32)	(0.30)	(0.379)	(0.392)
Year 2000	-0.327*	-0.308	0.325	0.377	-0.146	-0.189	-0.059	-0.071
	(0.18)	(0.16)	(0.22)	(0.21)	(0.15)	(0.14)	(0.182)	(0.170)
Constant	-0.473***	-0.525***	-1.616***	-1.637***	-0.458***	-0.473***	-0.952***	-0.84***
	(0.14)	(0.13)	(0.18)	(0.17)	(0.13)	(0.12)	(0.152)	(0.140)
N	1242
Notes: Standard errors are in parentheses. *, , and * denote p<0.01, p<0.05, and p<0.1 respectively.

Table 6: Point-Prevalence Estimates for Cocaine, Heroin, and Marijuana Use in Portland

Drug

Method 1

Method 2

Method 3

Cocaine

0.252

(0.013)

0.248

(0.01)

0.243

(0.013)

Heroin

0.143

(0.01)

0.135

(0.009)

0.132

(0.010)

Marijuana

0.376

(0.014)

0.371

(0.012)

0.365

(0.015)

Methamphetamine

0.221

(0.012)

0.226

(0.011)

0.226

(0.013)

Notes: Standard errors are presented in parentheses

1 The ten ADAM I sites from 2007-2011 were Atlanta, GA (Fulton County), Charlotte, NC (Mecklenburg County), Chicago, IL (Cook County), Denver, CO (Denver County), Indianapolis, IN (Marion County), Minneapolis, MN (Hennepin County) New York, NY (Borough of Manhattan), Portland, OR (Multnomah County), Sacramento, CA (Sacramento County) and Washington, D.C. (District of Columbia).

2 The movement from arrest by local police to booking and arraignment can differ. In most of the ADAM II sites, local or city police arrest an individual and, even if held temporarily at a local station house, transport him to the county facilities where he is charged and appears before a magistrate. The discretion to release minor offenders before booking or with a citation only varies by state law, and those offenders are not in the ADAM II samples.

3 The city of Atlanta sits in two counties: Fulton and DeKalb. The city police book in Fulton County because it represents the largest geographic segment of the city.

4 The sample is selected within a 24 hour period. However, the arrest may have occurred outside that 24 hour period, especially if the arrestee was held temporarily in a local holding facility for several hours. ADAM II imposed a 48 hour rule for the arrest period to assure that the urine test is valid.

5 This assumes selection on observables. This means that inclusion in the sample is random, conditioned on the estimated propensity score. One cannot be sure this condition holds, but nearest neighbor replacement sampling helps assure that the condition is met, and the use of propensity score weighting reduces bias when the condition is not met exactly.

6 Although Wooldridge offers one approach to adjusting standard errors, other authorities offer alternative approaches, and according to Morgan and Winship (2007), there is no universal standard. As statistical theory and statistical software evolve, future versions of ADAM II will incorporate improved standard error estimation. Fortunately, current ADAM II testing using the Wooldridge approach suggests that standard errors are not seriously biased, so correcting them at this time is not critical.

7 The 2002/2003 contractor was unable to provide the census data for those years, so only 2000 and 2001 data were originally included.

8 The starting time H and the stopping time H+S are not always constant from day-to-day. Therefore, we cannot precode this summation to start at the beginning of the stock period and end at the termination of the stock period.

9 Again, ADAM II is not able to reweight data from 2002–2003, as the development of propensity scores requires each site’s census data for each quarter. These data are not available from the prior ADAM contractor. Census data from 2000–2001 were kept in-house by Abt Associates, the contractor for those years.

10There is an important assumption: Failure to provide a urine test must not be correlated with recent drug use conditional on the response to the 3-day question. Put another way, among those respondents who denied using cocaine, those who did and those who did not use cocaine must be equally likely to provide a urine test. This assumption is not testable. Even if the assumption is incorrect, Schaefer (1997) argues that imputation will reduce bias that will otherwise arise from discarding data for arrestees who fail to provide urine specimens.

11 In early applications of the imputation methodology, the analysis team applied step 4, but failed to apply step 3. This caused the standard errors to be slightly underestimated. This error is corrected in the current estimation methodology.

12 The imputations could be done with a logistic regression, but especially when dealing with drugs whose use is infrequent, the logistic regression is increasingly unstable as more variables are added as conditioning variables. The reason is that unique combinations of variables result in a probability of 1 or 0, in which case no estimate is possible. Dealing with this problem is straightforward for a single regression, but is problematic in an automated estimation procedure.

13 Note that this is the second step of the two-step estimator that Wooldridge (2003) proposes in the presence of nonrandom selection.

14 As noted earlier, census data for 2002 and 2003 are not available. In these analyses, the propensity score weights calculated for 2000 and 2001 and the original ADAM weights for 2002 and 2003 are used (because census data for those years is not available). All ADAM II estimates (2007-2012) use the new propensity score weights.

15 Note that when weights are employed, it is not appropriate to use a likelihood ratio test.

16 Joint significance means a test of the null hypothesis that the offense category does not affect the probability of testing positive (the first test) and a test of the null hypothesis that seasonality does not affect the probability of testing positive (the second test).

17 As noted in footnote 4, statistical theory and software to improve standard error estimation in models such as those used in ADAM II are still evolving. The analytic team follows this literature and will incorporate improved estimation techniques as they develop.

18 The same estimation procedures and diagnostic steps described here are conducted with all sites each quarter.

19 For ADAM II, all statistics are annualized. This is necessary because yearly reports (2000-2003, 2007-2012) are based on different quarters of data; e.g., three or four quarters for sites in 2000-2003, two quarters in 2007-2011 and one 21 day period in 2012). Estimating variation over the quarters allows annualization, removing the quarter effects. Consequently, data from 2007-2012 are annualized. The annualization process is described in Section 5.2.

Abt Associates Inc. Technical Report 4

File Type	application/vnd.openxmlformats-officedocument.wordprocessingml.document
Author	AAlmozlino
File Modified	0000-00-00
File Created	2021-01-30