Employee Benefits Security Administration Participant Assistance Program Customer Survey Justification
Employee Benefits Security Administration Participant Assistance Program Customer Survey Supplemental Supporting Statement(20130724).docx
DOL Generic Solution for Customer Satisfaction Surveys and Conference Evaluations
Employee Benefits Security Administration Participant Assistance Program Customer Survey Justification
OMB: 1225-0059
OMB Approval No. 1225-0059
CUSTOMER SATISFACTION SURVEY AND CONFERENCE EVALUATION CLEARANCE FORM
A. SUPPLEMENTAL SUPPORTING STATEMENT
A.1. Title: |
EBSA Participant Assistance Program Customer Survey |
||||
A.2. Compliance with 5 CFR 1320.5: Yes X No _____ |
A.3. Assurances of confidentiality: No confidential data will be collected.
|
||||
A.4. Federal cost: $572,431.69 Based on the cost for research contractor and for IT contractor for support |
A.5. Requested expiration date (Month/Year): 01/2016
|
||||
A.6. Burden Hour estimates:
a. Number of Respondents: 6380 a.% Received Electronically 0% b. Frequency: Once c. Average Response Time: 8 minutes d. Total Annual Burden Hours: 851 hours
|
A7. Does the collection of information employ statistical methods?
__ ____ Yes (Complete Section B and attach BLS review sheet).
|
||||
A.8. Abstract: This survey will collect customer satisfaction data for a sample of private citizens who call into the participant assistance program to ask about their private sector employer provided benefits such as pensions, retirement savings, and health benefits. Three types of callers will be queried: 1. Those who need benefit claim assistance 2. Those who have a valid benefit claim and 3. Those who have an invalid benefit claim.
|
|||||
Program Official Terri Thomas
|
Date 07/24/2013 |
Departmental Clearance Officer Michel Smyth |
Date 07/24/2013 |
||
SURVEYS AND EVALUATIONS EMPLOYING STATISTICAL METHODS
B.1. Describe (including a numerical estimate) the potential respondent universe and any sampling or
other respondent selection methods to be used. Data on the number of entities (e.g., establishments, State and
local government units, households, or persons) in the universe covered by the collection and in the
corresponding sample are to be provided in tabular form for the universe as a whole and for each of the
strata in the proposed sample. Indicate expected response rates for the collection as a whole. If the collection
had been conducted previously, include the actual response rate achieved during the last collection.
The goal of this study is to evaluate EBSA’s Participant Assistance Program (PAP) and the universe consists of participant inquiries (individuals who had contacted EBSA for assistance) handled by the 10 regional offices and the Office of Participant Assistance (OPA). Inquiries are made by telephone as well as using letters, emails, web-based inquiries and walk-in visits. For each of the 10 regional offices, the universe includes only telephone inquiries. For the OPA, the universe will consist of mail and web inquiries. For the purpose of sampling, the universe will be stratified into 11 strata (the 10 regional offices and the OPA as shown in Table 1 below) and sampling will be done independently within each office using a simple stratified sample design. Table 1 below provides the approximate number of “closed” inquiries (web/mail inquiries for the OPA and telephone inquiries for the rest of the offices) during FY2012.
Table 1: Closed Inquiries by 11 offices during FY2012
-
Regional Office
Number of Inquiries
Atlanta
33,079
Boston
13,431
Chicago
13,672
Cincinnati
19,880
Dallas
16,922
Kansas City
14,229
Los Angeles
13,320
New York
13,321
Philadelphia
12,936
San Francisco
14,775
OPA
4,613
Total
170,178
Every two weeks, EBSA will send data on all of the participant inquiries identified as newly “closed” during the previous two weeks. The newly closed cases consist of all inquiries assigned a determination or closure analysis status in the Technical Assistance Information System. Closure types include Benefit Claim- Assistance, Benefit Claim-Valid Recovery, Benefit Claim-Not Valid, Benefit Claim-Enforcement Lead or Benefit Claim-Secondary Enforcement Lead. [Gallup will select samples of participant inquiry records on a bi-weekly basis using a simple stratified sample design. Based on information from the past administration of this study conducted by Gallup for fiscal year 2012, we anticipate an average response rate of around 33.5% for each two-week period across all offices. In order to examine the issue of non-response bias, a non-response bias analysis will be conducted. The non-response bias analysis plan to be followed for this purpose is described in Section B3. In total for FY2013, there will be 24 two-week data collection periods. The goal will be to complete a total of about 24 interviews from each of the 11 offices in each period so that a total of 576 (= 24 X 24) interviews can be completed for each office over the course of the 24 periods of data collection. The total number of interviews across all offices is therefore estimated to be around 6,336 (=576 X 11).
The population parameter of primary interest will be the proportion of customers in specific categories. For example, the “proportion of customers in the population who are satisfied with EBSA overall” or the “proportion of customers who think EBSA is a name they can trust” will have to be estimated based on survey data. The corresponding sample estimates will be computed based on responses to the survey. On a satisfaction question such as : “How satisfied are you with EBSA overall?”, the proportion of satisfied customers may be estimated based on the proportion selecting one of the top two boxes on a 5-point likert scale. Customers will also be asked to indicate their level of agreement with statements like “EBSA is a name I can always trust” or “EBSA always delivers on what they promise” on a 5-point scale. The proportion of customers who select one of the top two boxes will provide an estimate of the corresponding population proportion. The sample based estimate (p) of the parameter representing an unknown population proportion (P) can be expressed as:
p
=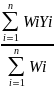 ,
,
where Yi = 1 if the ith sampled respondent belongs to the category of interest (satisfied, for example) and 0 otherwise; Wi is the sample weight attached to the ith respondent and ‘n’ is the number of completed surveys.
These parameters (proportions or means) may have to be estimated at the overall EBSA level, for each of the 11 strata (offices) separately and possibly for other domains of interest within each stratum. For example, it may be of interest to generate similar estimates by the three Closure Types: (i) those who need benefit claim assistance (ii) those who have a valid benefit claim and (iii) those who have an invalid benefit claim. The bulk of the calls (about 80 to 90% on an average) will belong to the first Closure type (those who need benefit claim assistance) and hence the number of completed surveys within each stratum for this subgroup will be large enough (around 500) to generate estimates of acceptable precision. Similar estimates for the other two Closure types can also be generated but the sample size within individual offices will be low and hence the estimates for these two Closure types may have to be generated at the overall EBSA level.
B.2. Describe the procedures for the collection of information including:
• Statistical methodology for stratification and sample selection – The universe of all telephone inquiries will be stratified by the 10 offices such that each office will be a separate stratum. For the OPA office, the universe will consist of all web and mail inquiries. The bi-weekly files to be transmitted from EBSA to the contractor for the purpose of sampling will contain variables necessary to link each inquiry to a particular office. Within each stratum, a simple random sample of specified size will be drawn independently once every two weeks. The initial sample size within each stratum for every two week period will be large enough to yield around 24 completed interviews. Based on an anticipated response rate of 33.5 percent (adjusted for eligibility) and taking into account the expected loss due to ineligibility, we will sample about 85 inquiries on an average for each two week data collection period. That should on an average yield 24 completed surveys. The response rate may actually vary across the data collection period or across different offices and so the sample sizes will be continuously adjusted based on observed response rates at the office level to meet the target for the number of completed surveys.
• Estimation procedure – Sample data will be weighted to generate unbiased estimates for the target population subgroups. Within each stratum, weighting will be carried out to adjust for (i) probability of selection in the sample and (ii) non-response. Once the sampling weights are generated, weighted estimates will be produced for different unknown population parameters (means, proportions etc.) for the target population and also for population subgroups of interest. For the purpose of illustration, let us assume that we receive a total of 1,600 inquiries in a stratum (or regional office) in a particular two-week period and we select a random sample of size 80 from those 1,600 inquiries. Also, assume that 24 of those 80 sampled cases actually respond i.e. we get 24 completed surveys. The weight assigned to each of those 24 completed surveys will consist of two weighting factors: (i) selection probability weight (1600/80) and (ii) non-response weight (80/24). The first weighting factor is the inverse of the selection probability while the second factor is the ratio of the sample size and the number of completed surveys. The final weight will be the product of these two factors. In this specific example, the final weight assigned to each of those 24 completed cases will be (1,600/80) * (80/24) = 1,600/24. The sum of the weights of these 24 cases will add up to 1,600, the total number of inquiries for that two-week period.
Based on our previous experience in conducting this survey, we do expect some “ineligible” cases in the sample. The weighting procedure can be easily adjusted to account for ineligible cases. If, for example, 8 out of the 80 sampled cases turn out to be ineligible, the non-response weight factor will be equal to 72/24 and then the final weight assigned to each of the 24 completed surveys will be (1600/80)*(72/24). The sum of the weights for all 24 cases will then equal 24*(1600/80)*(72/24) = 1440, the estimated number of eligible cases in the population during that particular data collection period.
In
terms of mathematical symbols, the weighting steps can be described
as follows. Let
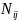 and
and
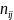 denote
the population size (total number of cases received) and the
corresponding sample size (number of cases sampled) for any
particular office i (i=1,2, …,11) and for a specific two-week
data collection period j (j=1,2,…,24). Also, let
denote
the population size (total number of cases received) and the
corresponding sample size (number of cases sampled) for any
particular office i (i=1,2, …,11) and for a specific two-week
data collection period j (j=1,2,…,24). Also, let
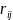 denote the number of responding units in the sample in ith
office and jth
data collection period. Then, the base-weight or the probability
weight factor (
denote the number of responding units in the sample in ith
office and jth
data collection period. Then, the base-weight or the probability
weight factor (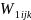 )
assigned to kth
sampled unit (k=1, 2, …,
)
assigned to kth
sampled unit (k=1, 2, …,
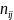 )
will be derived as:
)
will be derived as:
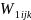 =
Nij/nij…
(1)
=
Nij/nij…
(1)
At
the next step, the non-response adjustment factor (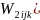 will be derived as:
will be derived as:
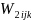 =
=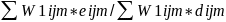 … (2)
… (2)
if the kth unit (k=1, 2, …, nij) is a responding unit and 0 otherwise;
eijm = 1 if the mth unit in the sample is eligible and 0 otherwise; dijm = 1 if the mth unit is eligible and responds to the survey and 0 otherwise.
In the right hand side of equation (2) above, note that the summation in the numerator is over all sampled eligible cases whereas the summation in the denominator is over all selected eligible persons who actually respond to the survey.
The final weight (Wijl) assigned to all rij responding units (in ith office in jth data collection period) will be the product of the two weighting factors:
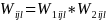 …
(3) (l = 1, 2, …,
rij).
…
(3) (l = 1, 2, …,
rij).
The simple random samples drawn during each data collection period within each office are likely to include proportional representation of cases (inquiries) by Closure types (those who need benefit claim-assistance, those who have a valid benefit claim, and those who have an invalid benefit claim). Construction of non-response adjustment cells based on Closure types may be considered. However, for most strata (offices), the bulk of the calls (80 to 90%) are likely to belong to the first Closure type category (those who need benefit claim assistance) only and the number of calls belonging to the other two types (valid and invalid) will be small. Collapsing of non-response adjustment cells, therefore, will be necessary. We anticipate using rules based on the (i) size of the cell and (ii) value of the non-response adjustment factor. For this study, given that bulk of the calls will belong to the first category only, we anticipate using the entire stratum as the non-response adjustment cell for most strata. In some strata, it may be possible to use two cells (those who need benefit claim assistance and Others). The non-response weighting adjustment procedure within each of these non-response adjustment cells will be the same as described above.
• Degree of accuracy needed for the purpose described in the justification – For each stratum (office), the total number of completed interviews over the 24 data collection periods will be around 576. For estimation of any unknown population proportion (P), for example, this will result in a margin of error of 4 percent at the 95% level of significance ignoring any design effect. The margin of error (MOE) for estimating the unknown population proportion ‘P’ at the 95% confidence level can be derived based on the following formula:
MOE
= 1.96 *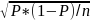 where ‘n’ is the sample size (i.e. the number of
completed surveys).
where ‘n’ is the sample size (i.e. the number of
completed surveys).
Under
the most conservative assumption (P=0.5), the MOE for a sample size
of 576 will be 1.96*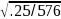 =
4.08%. Based on the past data, the average design effect within each
stratum is not expected to exceed 1.2 and hence the sampling error is
likely to be in 4% to 5% range for estimates at the individual office
level. It may be noted that, for any given office, the allocation of
sample across all 24 data collection periods is not strictly
proportional because a fixed number of completed surveys (24) will be
targeted in each two-week period. However, for the same office, the
total number of cases (inquiries) is not expected to vary
significantly over time and hence its impact on design effect for
estimates based on data for several data collection periods should be
minimal.
=
4.08%. Based on the past data, the average design effect within each
stratum is not expected to exceed 1.2 and hence the sampling error is
likely to be in 4% to 5% range for estimates at the individual office
level. It may be noted that, for any given office, the allocation of
sample across all 24 data collection periods is not strictly
proportional because a fixed number of completed surveys (24) will be
targeted in each two-week period. However, for the same office, the
total number of cases (inquiries) is not expected to vary
significantly over time and hence its impact on design effect for
estimates based on data for several data collection periods should be
minimal.
At
the overall agency level, the total sample size will be around 6,336
and hence the MOE is expected to be around 1.96*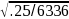 =
1.2% under the assumption of no design effect. However, at the agency
level, the disproportional sample allocation across different offices
will contribute to the design effect. The design effect
was defined formally by Kish (1965) , Section 8.2, p. 258) as “the
ratio of the actual variance of a sample to the variance of a simple
random sample of the same number of elements.” Based
on Kish’s approximate formula
=
1.2% under the assumption of no design effect. However, at the agency
level, the disproportional sample allocation across different offices
will contribute to the design effect. The design effect
was defined formally by Kish (1965) , Section 8.2, p. 258) as “the
ratio of the actual variance of a sample to the variance of a simple
random sample of the same number of elements.” Based
on Kish’s approximate formula
{design effect= (sample size)*(sum of squared weights)/ (square of the sum of weights)},
the design effect at the overall agency level based on past data is expected to be around 1.72. After accounting for an expected estimate of design effect equal to 1.72, the margin of error for estimates of population proportions at the overall agency level based on a sample size of 6,336 will be about 1.6%.
The sample size across all offices within a quarter will be 6336/4=1584. For testing of hypotheses for the difference in proportions between quarters, a difference of 5% in proportions (minimal detectable effect) can be detected based on this sample size with α=0.05 and 80 percent power ignoring design effect when the proportion is about 50% in one quarter and 45 percent, for example, in another. Under the assumption of a design effect of 1.72, the minimal detectable effect size based on quarterly sample will be around 6.5% when the proportion is about 50% in one quarter and 43.5 percent, for example, in another. The formulas for two-sample proportion test are:
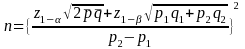 [1-tailed test]
[1-tailed test]
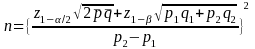 [2-tailed test]
[2-tailed test]
In these expressions,
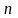 is the sample size required to
achieve the desired statistical power;
is the sample size required to
achieve the desired statistical power;
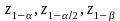 are
the normal abscissas that correspond to the respective probabilities;
are
the normal abscissas that correspond to the respective probabilities;
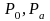 are the null and alternative
hypothesis in the one-sample test;
are the null and alternative
hypothesis in the one-sample test;
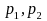 are
the two proportions in the two-sample test;
are
the two proportions in the two-sample test;
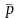 is the simple average of
is the simple average of
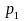 and
and
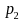 and
and
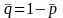 .
.
The sample size for any particular office for the entire fiscal year will be around 576. For comparison between two offices, a difference of 8% in proportions (minimal detectable effect) can be detected based on this sample size with α=0.05 and 80 percent power ignoring design effect when the proportion is about 50% in one quarter and 42 percent, for example, in another. The design effect within an office, as mentioned earlier, is not likely to exceed 1.2. Based on the assumption of a design effect of 1.2, a difference of 9% in proportions (minimal detectable effect) can be detected based on this sample size with α=0.05 and 80 percent power ignoring design effect when the proportion is about 50% in one quarter and 41 percent, for example, in another.
• Unusual problems requiring specialized sampling procedures and – We don’t foresee any unusual problems requiring specialized sampling procedures.
• Any use of periodic (less frequently than annual) data collection cycles to reduce burden – For this study, Gallup will sample once every two weeks and the data collection for every bi-weekly sample will be completed within the following two weeks. The data collection will therefore be a continuous process throughout the year but every respondent will be contacted/interviewed within two weeks after his/her inquiry is closed. This will be done to minimize the recall error and thereby increase the overall accuracy of the survey data.
B.3. Describe methods to maximize response rates and to deal with issues of non‑response. The accuracy and reliability of information collected must be shown to be adequate for intended uses. For collections based on sampling, a special justification must be provided for any collection that will not yield "reliable" data that can be generalized to the universe studied.
Methods to maximize response rates – In order to maximize response rates, Gallup will utilize a comprehensive plan that focuses on (1) a call design that will ensure call attempts are made at different times of day and different days of the week to maximize contact rates, (2) conducting an extensive interviewer briefing prior to the field period that educates them about the content of the survey as well as how to handle reluctance and refusals, (3) having strong supervision that will ensure that high quality data are collected throughout the field period, and (4) utilizing troubleshooting teams to attack specific data collection problems that may occur during the field period. Gallup will use a 5+5 call design i.e. a maximum of five calls will be made on the phone number to reach the specific person that we are attempting to contact and another up to five calls will be made to complete the interview with that selected person.
Issues of Non-Response: Survey based estimates for this study will be weighted to minimize any potential bias including any bias that may be associated with unit level non-response. The bi-weekly files (sampling frames) to be received from DOL will contain some useful information (like Closure types) for all cases including the non-respondents. Non-response adjustment cells, if found necessary, will be formed based on these variable and then ratio type adjustments will be carried out to correct for non-response. This will make the non-response weighting procedure quite effective in terms of minimizing non-response bias, if any. The data collection mode for this study is telephone and so the item non-response rate is expected to be less compared to data collected using self-administered modes. The respondent will however have the opportunity to refuse to answer a specific question. The item missing rate is not expected to be significant and so imputation of missing item level data was not used in the past and is not recommended for the 2013 study.
As described above in Section B2, the sampling error associated with estimates of proportions at the individual office level is expected to be in the 4% to 5% range and that for the overall agency level is not likely to exceed 1.5% at the 95% level of confidence. For any other subgroup of interest (based on closure types, for example) the sampling error will depend on the sample size. Also, all estimates will be weighted to reduce bias. It will be possible to calculate the sampling error associated with any subgroup estimate in order to ensure that the accuracy and reliability is adequate for intended uses of any such estimate
Non-response Bias Analysis: A non-response bias analysis will be conducted to identify potential source of non-response bias. Non-response bias associated with estimates consists of two factors - the amount of nonresponse and the difference in the estimate between the groups of respondents and non-respondents. The bias of an estimate can be expressed mathematically as follows:
Bias (yr) = (1 – r) {E (yr – yn )}
where yr is the estimated characteristic based on survey respondents only, ‘r’ is the response rate and so (1 – r) is the nonresponse rate, yn is the estimated characteristic based on the non-respondents only, and E is the expectation for averaging over all possible samples.
Bias may therefore be caused by lower response rate and/or by significant difference in estimates between respondents and non-respondents. As described earlier in this section (B3), necessary steps will be taken to maximize response rates and thereby minimize any non-response bias that may be caused by low response rates. Also, non-response weighting adjustments (refer to “Issues of non-response” above) will be carried out to minimize potential non-response bias. However, despite all these attempts, non-response bias can still persist in estimates. The goal of the non-response bias analysis will be to identify potential sources of nonresponse bias on estimates and to identify potentially biased estimates.
The non-response bias analysis will compare the “Early” respondents to “Late” respondents on selected key variables of primary interest. The basic assumption in such an approach is that later respondents to a survey are more similar to non-respondents than are earlier respondents. In this study, data collection will be conducted using telephone and a respondent can receive anywhere between 1 and 10 calls to complete an interview. Respondents will be divided into two groups (Early and Late respondents) based on the number of calls received. The exact definition of these two groups will be finalized after examining the distribution of the ‘number of calls’ needed to complete an interview for this study. Comparison of estimates (proportions or means of selected key variables like proportion of satisfied customers, for example) between these two groups will be carried out by testing the hypothesis of equality of proportions (or means). The analysis can be done using non-response adjusted weights but can also be done using the base weights. This process will help identify estimates that may be subject to non-response bias.
The key variables (or survey questions) for the comparison of “Early” and “Late” respondents will include the following eight questions that are expected to be strong predictors of overall customer satisfaction. (Each of these eight questions uses a five-point scale, where 5 means strongly agree and 1 means strongly disagree and the respondent is asked to tell how much he or she agrees or disagrees with each statement as it applies to EBSA).
EBSA treats me like a valued customer
EBSA is willing to work with me to make sure my needs are met
EBSA acts in a timely fashion
EBSA does what it says it will do
EBSA services are available when I need them
EBSA is easy to reach
The information I receive from EBSA is clear and easy to understand
EBSA does its best to help me out
For each of these selected variables, the mean of the two groups (‘early’ and ’late’ respondents) will be compared based on a t- test using using software SUDAAN so that the sample design and the resulting sample weights can be taken into consideration.
Let the mean (or equivalently the proportion of 1s for a 0-1 variable) of ‘early’ and ‘late’ respondents for a specific variable (Y) based on survey data be denoted by p1 and p2 respectively. Then, p1 can be written as
p1 = ∑Wiyi/∑Wi, where yi is 1 if the value of variable Y for the ith respondent is 1 and ‘0’ otherwise; Wi is the weight assigned to the ith respondent and the summation in both numerator and denominator is over all ‘early’ respondents in the sample. p2 can be similarly defined. The t-statistic for testing the equality of means for those two groups (Ho: P1=P2 vs. H1:P1 ≠ P2 where P1 and P2 are the corresponding population means) will be computed as:
t=(p1 – p2)/SE (p1 – p2) , where SE (p1 – p2) is the standard error or the estimated square-root of the variance of (p1 – p2).
In order to obtain the value of t-statistic (and the corresponding significance level or p-value), the main SUDAAN commands using the DESCRIPT procedure will be as follows:
PROC DESCRIPT DATA=XXXX FILETYPE=SAS DESIGN=STRWR;
nest office_period;
WEIGHT FINALWT;
class early_late;
var Y;
contrast early_late = (1 -1)/name = "respondent vs. nonrespondent";
print nsum t_mean p_mean mean;
The variable office_period (obtained by crossing the levels of regional offices and data collection periods) will represent all the strata. The design STRWR is proposed in the design statement based on the assumption that the sampling fraction within each stratum will be small ( less than 10 percent). If that condition is not satisfied, the STRWOR (stratified without replacement) option will be used and necessary information (TOTCNT representing the total number of cases per stratum) will be included in the SUDAAN statements. The WEIGHT statement specifies the final weight variable. The CLASS statement defines the independent variables as categorical and REFLEVEL specifies the reference level for each of these variables.
The early_late variable will contain two distinct values (0-1 for example) to identify the two groups (‘early’ or ‘late’) for each case in the data set. The VAR statement will include the variables for which the mean has to be compared between the two groups. For each selected variable included in the VAR statement, the hypothesis of equality of means will be rejected (or not) based on the p-value (less than 0.05 or not).
Non-response bias analysis may also involve comparison of survey based estimates to known Population Values and/or (ii) External Estimates that may be available. For this study, variables like Subject entry code, Closure types and Date open and Date closed (of inquiry) will be available for all cases on the sampling frame. It is, therefore, possible to compute the actual value of population parameters that are functions of these variables and compare those with the corresponding sample based (weighted) estimates. For example, the following three population parameters may be used for this comparison.
P_BCA: Proportion of Benefit Claim Assistance (BCA) calls (derived from the Closure Analysis variable on the sampling frame)
M_Close: Mean of the variable Days to Close (derived based on Date Opened and Date Closed variables on the sampling frame)
P_PBS: Proportion of calls falling under a certain subject entry code (for example, the proportion of calls under PBS (Pension Benefits, Social Security Notice). This was derived from the Subject Entry Code variable on the sampling frame.
The corresponding sample-based weighted estimates for the three population parameters will be generated using the values of those variables from the completed surveys. The comparison will be carried out using a one-sample t-test based on a t-statistic = (p–P)/SE(p) where ”p” is the sample-based estimate of the corresponding population proportion (or mean) ”P,” and SE(p) is the estimated standard error of p. The main SUDAAN statements to be used for the computation of SE(p) for the variable “Days to Close”, for example, will be as follows:
PROC descript data = XXXX filetype = sas design = strwr;
NEST office_period;
WEIGHT finalwt;
VAR days_to_close;
PRINT nsum wsum mean semean;
[NEST statement specifies the strata determined by office and period (2-week data collection period) and FINALWT is the final weight variable. The VAR statement will include the variable (M_Close: Days to Close) for which the mean was to be compared between the two groups. The hypothesis of equality of means will be rejected (or not) based on the p-value (less than 0.05 or not).]
Once SE(p) is estimated using SUDAAN, the t-statistic will be calculated using the values of p and P, and the hypothesis of equality (p = P) will be rejected (or not) based on the observed significance level (less than 0.05 or not).
For the purpose of comparing survey based estimates with External estimates, the estimate of the proportion of satisfied customers (proportion of responses in the top two boxes on the overall satisfaction question) from the previous round of this survey may be used as an External estimate. The sample based estimate for the same proportion can be obtained from the current round of the survey and compared with that from the previous round. The comparison can be done based on a test of hypothesis of equality (as described above for comparison with population values). It is, however, noted that such comparisons may be subject to confounding factors (changes due to non-response bias or actual change in satisfaction level over time etc.) and the results may not be influenced by non-response only. However, the results of such comparison along with other findings of the non-response bias analysis may be helpful for examining the issue of non-response bias.
The non-response bias analysis plan described above will be carried out at the full population level and there is no plan to carry out similar analyses for any sub-populations.
B.4. Describe any tests of procedures or methods to be undertaken. – None.
B.5. Provide the name, affiliation (company, agency, or organization) and telephone number of individuals consulted on statistical aspects of the design and the name of the agency unit, contractor(s), grantee(s), or other person(s) who will actually collect and/or analyze the information for the agency.
Name |
Agency/Company/Organization |
Number Telephone |
Susan Conner |
Gallup Organization |
202-715-3124 |
Manas Chattopadhyay |
Gallup Organization |
202-715-3179 |
Camille Lloyd |
Gallup Organization |
202-715-3188 |
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | SUPPORTING STATEMENT FOR |
| Author | kurz-karin |
| File Modified | 0000-00-00 |
| File Created | 2021-01-29 |
© 2026 OMB.report | Privacy Policy