Att7_SampleSize PowerCalc
Att7_SampleSize PowerCalc.docx
Anniston Community Health Survey: Follow up and Dioxin Analyses (ACHS-II)
Att7_SampleSize PowerCalc
OMB: 0923-0049
Attachment 7
Anniston Community Health Survey: Follow-up Study and Dioxin Analyses
Sample Size and Power Estimation for Exposure Assessment
Part A. Sample size estimation for change in PCB congener value between Time 1 and Time 2
Study Design: One-time cross-sectional follow-up study seven years after baseline
Assumption 1: Metabolism and elimination of PCB congener follows an exponential decay model
Assumption 2: Additional individual exposure to PCB congener between Time 1 and Time 2 is minimal
Assumption 3: Change in PCB congener variable is lognormal
Null Hypothesis (HO): PCB congener concentration follows an exponential decay model (Seegal et al., 2011) where half-life (HL) = 14 years (for PBCs 118, 153, 206 based on Knobeloch et al., 2009).
Alternative Hypothesis (HA): PCB congener concentration follows and exponential decay model, where half-life (HL) = 20 years or longer.
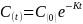 ,
where
,
where
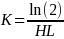
Let
x1,
. . . ., xn
denote the data at Time 1. Then x1
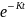 ,
. . . . , xn
,
. . . . , xn
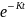 are the data at Time 2.
are the data at Time 2.
The change in PCB level for individual, i, is given by:
Change
= xi
– xi
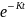 = xi
(1–
= xi
(1–
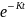 ).
).
Since we assume these variables are lognormal, we use a log-transformation to make the distribution normal.
g(x)
 ln
(Change) = ln [xi
ln
(Change) = ln [xi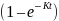 ]
= ln (xi)
+
ln (J),
]
= ln (xi)
+
ln (J),
where
J is the constant, (1–
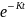 ).
).
We
can use a 2nd
order Taylor series around the mean,
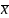 =
=
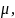 to approximate Var (g(x)). [See Dudewicz & Mishra, p263, Theorem
5.5.18]
to approximate Var (g(x)). [See Dudewicz & Mishra, p263, Theorem
5.5.18]
Var
(g(x))
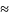 [g’ (
[g’ (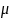 )]2
)]2
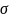 2,
2,
where
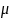 and
and
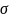 2
are the mean and the variance of the individual data. It follows that
2
are the mean and the variance of the individual data. It follows that
Var
(g(x))
 Var [ln (xi)
+ ln (J)]
Var [ln (xi)
+ ln (J)]
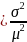 .
.
The
standard deviation of g(x)
is approximated by
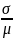 .
.
Restated, the standard deviation of the natural log of the change in PCB level is approximately equal to the standard deviation of the individual data divided by their mean.
Before calculating a sample size, it is worth noting that the mean change in PCB level is equal to the change in the mean.

Mean
Change in PCB Level = x1
(1–
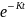 )
+ . . . . . . + xn
(1–
)
+ . . . . . . + xn
(1–
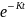 )
)
n
 =
(1–
=
(1–
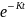 )(
x1
+
. . . . +
xn)
)(
x1
+
. . . . +
xn)
n
=
(1–
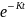 )
)
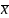 = Change in Mean PCB Level
= Change in Mean PCB Level
Thus on the natural log scale,
Mean
ln (Change in PCB Level) = ln (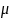 )
+ ln (J)
)
+ ln (J)
Example for representative low, moderately, and highly chlorinated PCB congeners using NCSS Power Analysis and Sample Size (PASS) 2008 Software, Kayesville, UT:
Test for One-Sample T-Test: HO: HL = 14 years vs. HA: HL ≥ 20 years
Under HO,
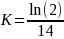 = 0.04951 and J = (1–
= 0.04951 and J = (1–
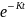 )
= 0.2929
)
= 0.2929
Under HA,
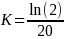 = 0.03466 and J = (1–
= 0.03466 and J = (1–
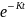 )
= 0.2154
)
= 0.2154
For PCB 118:
From
Time 1, based on serum PCBs from n=765 ACHS participants, assume
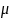 = 70, σ = 177, and Var [ln (Change)] = 177/70 = 2.5286.
= 70, σ = 177, and Var [ln (Change)] = 177/70 = 2.5286.
HO:
Mean
ln (Change in PCB Level) = ln (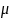 )
+ ln (J) = ln (70) + ln (0.2929)
)
+ ln (J) = ln (70) + ln (0.2929)
= 3.0206
HA:
Mean
ln (Change in PCB Level) = ln (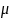 )
+ ln (J) = ln (70) + ln (0.2154)
)
+ ln (J) = ln (70) + ln (0.2154)
= 2.7132
A
sample size of 420 achieves 80% power to detect a difference of 0.3
between the null hypothesis mean of 3.0 and the alternative
hypothesis mean of 2.7 with an estimated standard deviation of 2.5
and
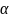 = 0.05, using a one-sided one-sample t-test.
= 0.05, using a one-sided one-sample t-test.
For PCB 153:
From
Time 1, based on serum PCBs from n=765 ACHS participants, assume
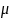 = 218, σ = 409, and Var [ln (Change)] = 409/218 = 1.8761.
= 218, σ = 409, and Var [ln (Change)] = 409/218 = 1.8761.
HO:
Mean
ln (Change in PCB Level) = ln (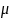 )
+ ln (J) = ln (218) + ln (0.2929)
)
+ ln (J) = ln (218) + ln (0.2929)
= 5.3845 - 1.2279 = 4.1566
HA:
Mean
ln (Change in PCB Level) = ln (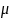 )
+ ln (J) = ln (218) + ln (0.2154)
)
+ ln (J) = ln (218) + ln (0.2154)
= 5.3845 - 1.5352 = 3.8492
A sample size of 232 achieves 80% power to detect a difference of 0.3 between the null hypothesis mean of 4.2 and the alternative hypothesis mean of 3.8 with an estimated standard deviation of 1.9 and with a significance level (alpha) of 0.05 using a one-sided one-sample t-test.
For PCB 206:
From
Time 1, based on serum PCBs from n=764 ACHS participants, assume
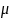 = 40, σ = 98, and Var [ln (Change)] = 98/40 = 2.4500.
= 40, σ = 98, and Var [ln (Change)] = 98/40 = 2.4500.
HO:
Mean
ln (Change in PCB Level) = ln (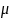 )
+ ln (J) = ln (40) + ln (0.2929)
)
+ ln (J) = ln (40) + ln (0.2929)
= 3.68887945 - 1.22792403 = 2.4610
HA:
Mean
ln (Change in PCB Level) = ln (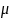 )
+ ln (J) = ln (40) + ln (0.2154)
)
+ ln (J) = ln (40) + ln (0.2154)
= 3.68887945 - 1.53525851 = 2.1536
A sample size of 395 achieves 80% power to detect a difference of 0.3 between the null hypothesis mean of 2.5 and the alternative hypothesis mean of 2.2 with an estimated standard deviation of 2.5 and with a significance level (alpha) of 0.05 using a one-sided one-sample t-test.
References:
Dudewicz, E.J., Mishra, S.N., 1988. Modern Mathematical Statistics. John Wiley & Sons, Inc., New York.
Knobeloch, L., Turyk, M., Imm, P., Schrank, C., Anderson, H., 2009. Temporal changes in PCB and DDE levels among a cohort of frequent and infrequent consumers of Great Lakes sportfish. Environ. Res. 109(1), 66-72.
Seegal, R.F., Fitzgerald, E.F., Hills, E.A., Wolff, M.S., Haase, R.F., Todd, A.C., Parsons P., Molho, E.S., Higgins, D.S., Factor, S.A., Marek, K.L., Seiby, J.P., Jennings, D.L., McCaffrey, R.J., 2011. Estimating the half-lives of PCB congeners in former capacitor workers measured over a 28-year interval. J. Exposure Sci. Environ. Epi. 21, 234–246.
Part B. Power estimation to detect difference in PCB levels between incident diabetes cases and non-diabetics
Method: Two-Sample T-Test Power Analysis
Estimated number of incident diabetes cases:
We estimate to enroll 365 persons without diabetes (out of 500 total). To estimate the total number of incident diabetes cases we used combined average rate of 9.5 /1,000 per year for 255 normoglycemic individuals and 50/1,000 for 110 pre-diabetics over the average of 7 years of follow up (See Section B.1 – Sample Size).
Supplemental Table 1. Estimated number of incident diabetes cases.
Year |
No. Available |
Rate per Year |
No. Incident Cases |
|
No. Available |
Rate per Year |
No. Incident Cases |
|
Normoglycemic |
|
Pre-Diabetic |
||||
|
|
|
|
|
|
|
|
1. |
255.0 |
0.0095 |
2.42 |
|
110.0 |
0.050 |
5.50 |
2. |
252.6 |
0.0095 |
2.40 |
|
104.5 |
0.050 |
5.23 |
3. |
250.2 |
0.0095 |
2.38 |
|
99.3 |
0.050 |
4.96 |
4. |
247.8 |
0.0095 |
2.35 |
|
94.3 |
0.050 |
4.72 |
5. |
245.4 |
0.0095 |
2.33 |
|
89.6 |
0.050 |
4.48 |
6. |
243.1 |
0.0095 |
2.31 |
|
85.1 |
0.050 |
4.26 |
7. |
240.8 |
0.0095 |
2.29 |
|
80.9 |
0.050 |
4.04 |
Total |
|
|
16.48 |
|
|
|
33.18 |
The calculations suggest that we can assume to detect an estimated 16 cases of incident diabetes in normoglycemic individuals and about 33 cases in pre-diabetic individuals in 7 years of follow up for a total of 49 cases.
Report Definitions:
Power is the probability of rejecting a false null hypothesis. Power should be close to one.
N1 (non-diabetics) and N2 (incident diabetics) are the number of items sampled from each population.
Alpha is the probability of rejecting a true null hypothesis. It should be small.
Beta is the probability of accepting a false null hypothesis. It should be small.
Mean1 is the mean of populations 1 and 2 under the null hypothesis of equality.
Mean2 is the mean of population 2 under the alternative hypothesis. The mean of population 1 is unchanged.
S1 and S2 are the population standard deviations. They represent the variability in the populations.
Numeric Results for Two-Sample T-Test:
Null Hypothesis: Mean1=Mean2. Alternative Hypothesis: Mean1<Mean2.
Assumptions: The standard deviations were assumed to be unknown and unequal.
Power N1 N2 Ratio Alpha Mean1 Mean2 S1 S2
0.865 316 49 0.155 0.05000 6.1 6.6 1.3 1.2
Summary Statements:
Group sample sizes of 316 and 49 achieve 86.5% power to detect a difference of -0.5 between the null hypothesis that both group means are 6.1 and the alternative hypothesis that the mean of group 2 is 6.6 with estimated group standard deviations of 1.3 and 1.2 and with a significance level (alpha) of 0.0500 using a one-sided two-sample t-test.
References:
Machin, D., Campbell, M., Fayers, P., Pinol, A., 1997. Sample Size Tables for Clinical Studies, second edition. Malden, MA, Blackwell Science.
Zar, J.H., 1984. Biostatistical Analysis, second edition. Englewood Cliffs, NJ, Prentice-Hall.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Office of Science |
| File Modified | 0000-00-00 |
| File Created | 2021-01-29 |
© 2025 OMB.report | Privacy Policy