Attachment B - Experimental Design
Attachment-B-Experimental-design-v4-42715.docx
Experimental Economic Research
Attachment B - Experimental Design
OMB: 0536-0070
OMB Control Number 0536-0070, expires 06/30/2016
Attachment B
Experimental Design Protocol
Overview
This document provides an overview of a lab experiment that examines the cost-effectiveness of alternative auction design mechanisms for an auction environment resembling USDA’s Conservation Reserve Program’s (CRP’s) General Signup. The CRP General Signup is a multi-unit, pay-as-bid, reverse auction. A consequence of the multi-unit, pay-as-bid approach is that the CRP runs a risk of paying substantial information rents. Currently the CPR uses a bid-cap approach based on estimates of reserve values to limit information rents. The goal of this research is to investigate the performance of alternative auction mechanisms designed to limit information rents. Conceptually, most of these mechanisms operate by accepting some higher cost bids to maintain competitive pressure on the lower cost bidders who have the most potential to extract information rents.
Key Design Terminology
Experiment – The experiment is composed of multiple 90-minute sessions. The number of sessions in an experiment is determined by the budget for the project and the statistical power required to test the primary research hypotheses.
Session – A session involves one group of participants, starts when we open the doors of the lab and ends 90 minutes later.
Treatment – A treatment, for the purposes of this experiment, is a particular auction structure (design). During each session the participants will participate in at least three different treatments, or types of auctions. Each treatment will consist of several rounds of that type of auction. For example, if there are three treatments and each treatment has five rounds, then a given session would consist of 15 total rounds, implying that each round would take about five minutes, leaving 15 minutes to provide participants with information about how the different auctions and the payoff structure operate.
Round – There will be multiple auctions, or rounds in each session. More rounds per treatment will allow for individuals to learn about both the incentive structure in each treatment as well as to update their beliefs about the distribution of valuation among the other participants in each auction. However, more rounds per treatment also limit the number of treatments that can be included per session.
Information rents: Participants within the experiment may learn how to use the information they acquire strategically to receive a rental payment in excess of their costs. – in excess over a normal market rent. This information rent will increase the cost to the buyer in the auction.
Experiment structure
Z-tree interface with internet administration
12 experimental sessions, 16 participants per session
3 treatments per session up to 15 rounds (based on pretesting, we predict an average of 12 rounds of each treatment, but subjects in different sessions often proceed at different speeds, making 15 rounds possible in some circumstances; in all cases we will maintain a 90 minute maximum experiment time.
Random order of treatment within session
Total of 5 treatments to be tested
Baseline (tight bid cap)
Loose cap
Reference price
Endogenous reference price
Grouping
-
Table 1. Experimental Design
Session
Treatment*
Average # of rounds per treatment
Max # of rounds per treatment
Time (in minutes)
# of participants
1
1,2,3
12
15
90
16
2
1,2,4
12
15
90
16
3
1,2,5
12
15
90
16
4
1,3,4
12
15
90
16
5
1,3,5
12
15
90
16
6
1,4,5
12
15
90
16
7
1,2,3
12
15
90
16
8
1,2,4
12
15
90
16
9
1,2,5
12
15
90
16
10
1,3,4
12
15
90
16
11
1,3,5
12
15
90
16
12
1,4,5
12
15
90
16
* Random order of treatment within session.
Payment
We will normalize payment so that the average payment is $25 per 1.5 hour session.
In the pretest, the average earnings were 45.81 Experimental Currency Units (ECU), with a minimum payment of 9 and a maximum payment of 106. In order to ensure that the average payment is $25, this implies a conversion factor of approximately 0.5. That is, one ECU will be worth $0.50. The high payment in this case would have been $53 and the low payment $4.50.
If
subjects bid less than their value and their bid is accepted, they
earn $(value - bid). If their bid is not accepted in a given
round, they earn $0.
They
will receive a cash payment based on the experimental market outcome
which results from each student’s behavior.1
The cash payment will be of uncertain value before the experiments
take place, but we do not expect any payments in excess of $5023
The average payments will be approximately $25. While a maximum cap
would be desirable, given that the market equilibriates within the
experiment and we are specifically testing a treatment without price
caps, we cannot guarantee that someone will not earn more than the
$50 if we calibrate the ECUs for a $25 USD average payment. The
payments listed here are for the entire 90 minute session, i.e. all
auctions participated in by a given individual. Although individuals
participate in many rounds within a session, individuals are paid at
the end of the 90 minute session based on 2 randomly-drawn rounds for
each auction type (for example, in a session for one treatement that
includes 12 rounds, experimentalists will draw two rounds at random
to be the auctions on which payment is based). This practice
prevents any wealth
effects from
distorting the findings of the experiment.4
This practice is standard in the literature.5
Therefore, their payments will be based on the sum of 6 randomly
drawn rounds: 2 per each auction type. Minimum payment will be 7
USD.
If more than 16 participants show up for the experiment, the last person(s) to have registered will receive 7 USD.
The
payments need to be set such that students are compensated for their
participation of 1.5 hours. Please see Mini Supporting Statement
Part A (section A.9) for further details and discussion of the
payment plan and its justification.
Auction
clearing
The auction will clear based on a fixed unit demand (as opposed to a budget-constrained auction). Assuming 16 participants (sellers) per experiment and a single unit available for each participant to sell, the buyer will accept 8 units. If all participants choose to make a bid, then this will result in a 50 percent bid-acceptance rate.
Key Auction Terminology
Unit: A unit is the item that participants are selling at auction. At the beginning of each round, each participant has one unit to sell.
Valuation:
The valuation of each unit (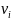 )
is private information about the cost (i.e.: “reserve value”
or “opportunity cost”) of each unit. Each participant
knows their own valuation, which is given to them at the beginning of
a round. Participants do not know each other’s valuations.
The buyer does not know any of the participants’ valuations.
)
is private information about the cost (i.e.: “reserve value”
or “opportunity cost”) of each unit. Each participant
knows their own valuation, which is given to them at the beginning of
a round. Participants do not know each other’s valuations.
The buyer does not know any of the participants’ valuations.
Reference
price: The buyer’s beliefs about the cost of
each unit (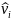 )
is semi-private information about the buyer’s beliefs. In some
treatments, participants learn the buyer’s estimate of their
own unit’s value. Participants are never told what the
buyer believes about the values of other participants’ units.
The reason that the buyer’s beliefs are disclosed is that these
beliefs are explicit determinants of key parameters in the auction
design. For example, in the simplest auction design, the buyer’s
estimate serves as an upper limit on each individual’s bid.
)
is semi-private information about the buyer’s beliefs. In some
treatments, participants learn the buyer’s estimate of their
own unit’s value. Participants are never told what the
buyer believes about the values of other participants’ units.
The reason that the buyer’s beliefs are disclosed is that these
beliefs are explicit determinants of key parameters in the auction
design. For example, in the simplest auction design, the buyer’s
estimate serves as an upper limit on each individual’s bid.
Determination of value
The first steps in running each round involve determining each participant’s valuation for the unit that they can offer in that round. The parameterization of the valuation process is an important part of the design of this experiment.
Each
unit’s value is determined by the following process:
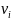 is
drawn from a uniform distribution U[10, 110].
is
drawn from a uniform distribution U[10, 110].
The
buyer can estimate the valuation
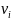 of each of the participants in the auction, and will try to use this
information to reduce the total cost of procuring units in the
auction. The buyer does not observe any valuation with perfect
precision, however. What the buyer actually observes is
of each of the participants in the auction, and will try to use this
information to reduce the total cost of procuring units in the
auction. The buyer does not observe any valuation with perfect
precision, however. What the buyer actually observes is
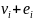 ,
where
,
where
 is an error term and
is an error term and
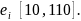
Treatments
Baseline (tight bid cap)
Bid cap = 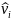
Loose cap
Identical to the baseline treatment, but the maximum bid is equal to
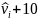
Reference price ranking
The buyer will use their estimate of
value to create a reference
price for each unit. The
reference price for each unit is equal to 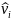 .
The score of each bid is equal to the bid divided by the reference
price. The buyer will accept the 8 bids with the lowest scores to
purchase, and will reject the remaining bids.
.
The score of each bid is equal to the bid divided by the reference
price. The buyer will accept the 8 bids with the lowest scores to
purchase, and will reject the remaining bids.
Endogenous reference price
The reference price for each unit is
equal to the average of the bids of bidders in the respective group.
The score of each bid is equal to the bid divided by the reference
price. The group of the ith
bidder is defined as the four nearest-neighbors in terms of the value
estimate ( 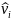 ).
The buyer will accept the 8 bids with the lowest scores to purchase,
and will reject the remaining bids.
).
The buyer will accept the 8 bids with the lowest scores to purchase,
and will reject the remaining bids.
Grouping
There are a maximum number of bids from
each group (A and B) that will be accepted by the buyer. These are
parameters controlled by the experimenter. There are 8 bidders in
group A and 8 bidders in group B. The 8 bidders with the lowest
values of 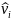 are in group A; the remainder are in group B. The buyer will accept
the 8 lowest bids to purchase, unless doing so causes the buyer to
accept more than the maximum number of bids from a given pool. If
the buyer is prevented from purchasing a unit because of the pool
limit, the buyer will select for purchase the eligible unit with the
next-lowest bid.
are in group A; the remainder are in group B. The buyer will accept
the 8 lowest bids to purchase, unless doing so causes the buyer to
accept more than the maximum number of bids from a given pool. If
the buyer is prevented from purchasing a unit because of the pool
limit, the buyer will select for purchase the eligible unit with the
next-lowest bid.
Outcomes of interest and power analysis
Outcomes
(1) Total procurement cost is the primary outcome of interest. Our power analysis is based on this primary outcome (see table and discussion below).
(2) A parameterized bidding function is a secondary outcome of interest. We will use a polynomial function of the value draws to estimate a bidding function bid = b(value). We will control for fixed factors with session and individual fixed-effects.
Power analysis
Each experiment will yield an average of 12 rounds of data per treatment ( three treatments—36 rounds of data). Because the 12 rounds are not independent (the same subjects participate in each of the rounds), we cluster at the session level. That is, the 36 observations generated in each session are not treated as independent. We are interested in the total procurement cost for each auction treatment; we obtain one (non-independent) observation of a given auction outcome each round. The requested number of burden hours allow us to conduct a total of 12 sessions. This means that we are conducting a test of means (mean procurement cost) clustered at the session level (12 clusters).
We have 12 sessions, each session yielding 36 observations. This gives us a total of 12*36 = 432 observations, or an average of 86 (rounded down) observations per auction treatment.
Based on an estimated average of 241.1 ECUs (Experimental Currency Units) and a standard deviation of 65 for the baseline treatment, the estimated minimum detectable effect (MDE) is 40.20.
The simulations used to determine the average procurement cost of 241.1 and the standard deviation of 65 are copied below in the Appendix.
Appendix
Simulations to determine expected cost of procurement for the baseline auction were run in the computer programming language R.
R is freely available at www.r-project.org/.
# What is the procurement cost of a baseline auction? These costs will be the basis of comparison to the three treatments
# Calculate based on simulations, with bidding behavior given by game theoretic analysis.
# The bidding behavior is given by:
# b*_i = cap_i if v_i < cap_i (the bidder will bid the cap if their underlying value is less than the cap, unless…
# b*_i = 0.3974+0.4210*v_i if v_i < 0.3974+0.4210*v_i < cap_i (the bidder trades off the probability of being accepted with receiving a higher payment if their optimal bid is less than the cap)
# b*_i = v_i if 0.3974+0.4210*v_i < v_i < cap_i (bidder will bid exact costs)
# Monte Carlo size
mc <- 10000
# Create a container variable for the cost of each iteration
cost <- rep(0,mc)
# Set seed
set.seed(12)
# Execute simulation
for (i in 1:mc) {
# Draw a random sample from [0,1]
v <- runif(16, min = 0, max = 1)
# Draw a buyer's estimate of value (equal to the price cap)
vHat <- v + runif(16, min = 0, max = 1)/20
# Bidding function
bTilda <- 0.3974+0.4210*v
b <- rep(0,16)
for (j in 1:16) {
if (v[j] < vHat[j]) {
b[j] <- vHat[j]
}
if ((v[j] < bTilda[j]) & (bTilda[j] < vHat[j])) {
b[j] <- bTilda[j]
}
if ((bTilda[j] < v[j]) & (v[j] < vHat[j])) {
b[j] <- v[j]
}
}
# Sort bids from lowest to highest
sb <- b[order(b)]
# Select the 8 lowest and sum the cost of enrolling them
cost[i] <- sum(sb[1:8])
}
# Multiply cost by 100 and add 10 to project onto proper scale
cost <- cost*100 + 10
# The average cost of an auction is:
summary(cost) # 241.10
# The sd of cost is:
sd(cost) # 64.96152
1 The number of auctions participated in by each individual within a session will be identical, but may vary across sessions. For more details, please see Attachment B - Experimental Design Protocol.
2 We are using $50 because the maximum payment in the pre-test which was less competitive (fewer people) than the proposed experiment was $53 when the ECU were converted into dollars.
3 Because auctions are competitive, it is not possible to directly limit the earnings that can be generated by participation without an explicit limit – a price cap. Because this experiment includes auctions without price caps as a very explicit treatment, it is not possible to guarantee that payments greater than $50 will not be made. Competition, however, is an excellent check on high payments. All auctions will be competitive and payments above $50 will be exceedingly rare. Furthermore, the payment design can be changed after the completion of a session, further reducing payment risk. That is, if in live testing – which by definition cannot be conducted at scale with 16 bidders until PRA clearance is received – individuals earn amounts in excess of the planned maximum, the rate of exchange between “experimental dollars” (the currency used in the experiment and displayed onscreen to the experiment participants) and $U.S. can be modified to ensure that payment stay within the proposed range in future sessions.
4 Wealth effects are the theoretical changes in behavior that occur after a given individuals’ wealth increases. Since the CRP is a “one-shot” auction – there is only one CRP auction conducted at a moment in time, not a series of CRP auctions – it is necessary to eliminate wealth effects.
5 See “Incentives in Experiments: A Theoretical Analysis” by Azrieli, Chambers, and Healy. http://www.econ.ucsb.edu/about_us/events/seminar_papers/Healy.pdf.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Wallander, Steve - ERS |
| File Modified | 0000-00-00 |
| File Created | 2021-01-26 |
© 2025 OMB.report | Privacy Policy