CVSA SS 011215 Part B - revised - May2015 -clean
CVSA SS 011215 Part B - revised - May2015 -clean.docx
Contingent Valuation/Choice Experiment Surveys for Hurricane Sandy Restoration Efforts in Forsythe National Wildlife Refuge in New Jersey and Jamaica Bay, NY
OMB: 0648-0714
SUPPORTING STATEMENT
Contingent Valuation/Choice Experiment Surveys for
Hurricane Sandy Restoration Efforts in
Forsythe National Wildlife Refuge in New Jersey and Jamaica Bay, NY
OMB CONTROL NO. 0648-xxxx
B. COLLECTIONS OF INFORMATION EMPLOYING STATISTICAL METHODS
1. Describe (including a numerical estimate) the potential respondent universe and any sampling or other respondent selection method to be used. Data on the number of entities (e.g. establishments, State and local governmental units, households, or persons) in the universe and the corresponding sample are to be provided in tabular form. The tabulation must also include expected response rates for the collection as a whole. If the collection has been conducted before, provide the actual response rate achieved.
ERG (NOAA’s subcontractor on this survey) will use GfK Knowledge Network’s online panel “Knowledge Panel.” GfK recruits its online panel members using a combination of random digit dialing (RDD) and address-based sampling (ABS). The ABS sampling allows for inclusion of cell-only households and non-internet households who join the panel are provided with computers to allow them to take the online surveys. Thus, GfK builds its internet panel from non-internet sources. This avoids some issues related to “opt-in” panels on the internet. The sampling frame we will use will be comprised of individuals living in the New Jersey and New York areas that were recruited by GfK, agreed to be part of the GfK panel, and were retained in the GfK panel at the time we implement our survey.
GfK claims that its panel is representative of the U.S. population:
“Representativeness of KnowledgePanel sample—including hard-to-reach groups such as young adults, males and minorities, for specific studies—has been documented in a number of papers and publications (Baker, Wagner et al 2003; Baker, Bundorf et al, 2003; Schlenger and Silver, 2006; Silver, Holman et al, 2002; Heeren et al, 2008; Chang and Krosnick, 2009; Baker et al, 2010; Yeager et al, 2011; Boxer, Aronson and Saxe, 2013).”1
The respondents will be selected from GfK’s panel from New Jersey, the New York City area, and selected counties in eastern Pennsylvania for the Forsythe survey and from New York and New Jersey for the Jamaica Bay survey. Eastern Pennsylvania was added to the Forsythe survey since individuals from eastern Pennsylvania may be familiar with Forsythe.
Response for our survey should reflect the response rates that GfK obtains in recruiting, onboarding, and retaining its panel, as well as the rate of completion of the survey we implement. GfK calculates four separate response/cooperation rates:
Recruitment rate: the percentage of those who were recruited that agreed to become part of the GfK panel. GfK quoted to ERG a current recruitment rate of 10%.
Profile rate: the percentage of those who agreed to become part of the panel who complete a demographics survey that GfK asks them to complete. Individuals who do not complete the demographics survey are not part of the panel. The current profile rate is 85%.
Completion rate: This is the percentage of people who complete surveys. This will vary from survey to survey and the one we implement with them will have its own completion rate. However, GfK suggested we use a value of 60% as an estimate for the completion rate.2
Retention rate: This is the percentage of people in the panel who remain in the panel from year to year. GfK’s estimated retention rate is 75%.
GfK has indicated that each of these rates iscalculated in ways consistent with AAPOR standards. Furthermore, they indicate that the appropriate method to calculate a response rate from these four rates is to multiply them together.3 Using the values provided by GfK indicates that the panel has a response rate of 6.4% (all rates except the completion rate). Accounting for the (expected) completion rate in the surveys we plan to implement implies a project response rate of 3.8% taking into account all of the rates quoted by GfK. We have provided a discussion of our approach to dealing with and analyzing non-response under Question B3 below. In calculating necessary sample sizes, however, we only use the completion rate in the tables that follow.
Table B-1 summarizes the number of households in each area and the associated sample to be selected from that area. Sample size calculations and selection are discussed under Question B2 below. NOAA expects to be able to attain a 60 percent or better completion rate in this survey since this survey involves a significant event (Hurricane Sandy). Stratification of the sample across states (“Percent of Sample from State” column) is discussed in Question B2 below.
Table B-1 – Respondent Universe and Sample Sizes
Area |
Total Number of Households, 2009-2013 (Universe) [a] |
Percent of Sample from State |
Sample Size |
Expected Completion Rate in Panel [b] |
Expected Number of Responses |
|
|||||
FNWR Salt Marsh Restoration Survey |
|||||
New Jersey |
3,186,418 |
60% |
500 |
60% |
301 |
New York [c] |
4,451,487 |
20% |
167 |
100 |
|
Eastern Pennsylvania [d] |
1,988,698 |
20% |
167 |
100 |
|
TOTALS |
9,626,603 |
|
834 |
501 |
|
|
|||||
Jamaica Bay Coastal Protection Survey |
|||||
New Jersey |
3,186,418 |
30% |
250 |
60% |
150 |
New York [c] |
4,451,487 |
70% |
584 |
350 |
|
TOTALS |
7,637,905 |
|
834 |
500 |
|
[a] Total household numbers were taken from Census Bureau data and reflect average number of households in the 2009-2013 time frame. See http://quickfacts.census.gov/qfd/index.html.
[b] The 60 percent completion rate assumption is based on response rates that GfK has been able to achieve through in its online survey efforts. NOAA has assumed that this represents a reasonable completion rate for our surveys.
[c] Includes the counties of New York (New York City), Richmond, Kings, Queens, Nassau, Suffolk, Bronx, Westchester, and, Rockland.
[d] Includes the counties of Bucks, Montgomery, Philadelphia, Delaware, Chester, Lehigh, Berks, and Lancaster.
2. Describe the procedures for the collection, including: the statistical methodology for stratification and sample selection; the estimation procedure; the degree of accuracy needed for the purpose described in the justification; any unusual problems requiring specialized sampling procedures; and any use of periodic (less frequent than annual) data collection cycles to reduce burden.
Necessary Sample Size (Degree of Accuracy)
The sample size for each survey was calculated using the rule of thumb developed by Johnson and Orme (1996)4 and summarized in Orme (2010).5 The rule of thumb value provides a minimum sample size needed for a choice experiment study that involves having respondents assess multiple alternatives in which the attributes of the alternatives have multiple levels. In our case, the alternatives are the salt marsh restoration options or coastal protection options that we are asking the respondents to vote on. The attributes are the different aspects or the restoration or coastal protection that we use to define the option’s benefits and cost.6 Each attribute has a set number of levels. Furthermore, the rule of thumb takes into account that each respondent can assess more than one set of alternatives. The rule of thumb is
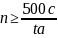
where
n is the (minimum) sample size,
t is the number of tasks that each respondent is being asked to perform. In our case, this is the number of alternative sets that we’ll ask each respondent to vote on. We will ask each respondent to vote on two different sets (t = 2)
a is the number of alternatives being presented to respondents each time they are asked to vote (excluding the “status quo” or “no action” scenario). In our case, we are asking respondents to compare two options each time (a = 2)
c is the number of levels for each attribute. In cases where the number of levels varies across the attributes, c is set equal to the largest number of levels for any attribute. For both surveys, the largest number of levels for any attribute is 4 (c = 4).
Using these values for t, a, and c in the rule of thumb results in an estimated sample size of 500 for each survey.
Stratification and Sample Selection
NOAA will be focusing on New Jersey, the New York City area, and selected counties in eastern Pennsylvania for the Forsythe NWR Salt Marsh Restoration survey and on the New York City area and New Jersey for the Jamaica Bay Coastal Protection survey. NOAA’s approach is to stratify by state for each survey. As noted, NOAA is targeting a sample of 500 respondents for each survey. Assuming a 60 percent completion rate, this implies selecting an initial sample of 834 respondents. To stratify the sample across states in each survey, NOAA has selected percentages for each state in the sample. For the Forsythe NWR survey, NOAA has selected 60 percent for New Jersey and 20 percent for the New York City area and eastern Pennsylvania. The concentration on New Jersey reflects the fact that Forsythe is located in New Jersey. For the Jamaica Bay survey, NOAA has selected 70 percent for the New York City area and 30 percent of sample for New Jersey. NOAA selected 70 percent for the New York City area since Jamaica Bay is located in New York.
Table B-2 – Stratification and Sample Size by State
Area |
FNWR Salt Marsh Restoration Survey |
Jamaica Bay Coastal Protection Survey |
||||
Percentage for State |
Initial Sample |
Expected Sample |
Percentage for State |
Initial Sample |
Expected Sample |
|
New Jersey |
60% |
500 |
301 |
30% |
250 |
150 |
New York [b] |
20% |
167 |
100 |
70% |
584 |
350 |
Eastern Pennsylvania [c] |
20% |
167 |
100 |
- |
- |
- |
TOTALS |
100% |
834 |
501 |
100% |
834 |
500 |
[a] Reflects English-speaking households only.
[b] Includes the counties of New York (New York City), Richmond, Kings, Queens, Nassau, Suffolk, Bronx, Westchester, and, Rockland.
[c] Includes the counties of Bucks, Montgomery, Philadelphia, Delaware, Chester, Lehigh, Berks, and Lancaster.
Estimation
To analyze the data that are collected from the surveys, NOAA will use a multinomial logisitic (MNL) regression analysis. MNL regression is the standard approach for analyzing choice experiment data. Before describing our use of MNL to derive values, we will provide some context on the analytical data set. First, respondents will represent multiple records in the final analytical data set. For example, for Forsythe, we are asking each individual to make a choice from two separate choice sets and each set has three choices (e.g., “Status quo,” “Option A,” and “Option B”). Thus, each response to the survey represents six records in the data (2 choice sets × 3 options to choose from within each set). Each record will have a binary variable set equal to 1 (= yes) if the respondent selected that option or 0 (= no) if the respondent did not select that option.7 Second, although the attributes we have included have quantitative levels, the data should be thought of as discrete in nature.8 For example, in the Forsythe survey, we will use four separate levels for the number of homes protected from storm surge: 1,000, 3,000, and 6,000, as well as and an implied “no additional” as part of the status quo. We cannot treat this as continuous data, but need to define four binary variables:
Alternative included no additional homes to be protected, yes or no.9
Alternative included 1,000 additional homes protected, yes or no.
Alternative included 3,000 additional homes protected, yes or no.
Alternative included 6,000 additional homes protected, yes or no.
Only one of these can be equal to one for any record in the database.10 Each other attribute would be treated similarly. Finally, the value for cost to respondent is used in its quantitative form. For example, if the cost for the option was listed as $100, then the value for the cost variable is simply 100. This is necessary to derive willingness to pay values.
The MNL regression analysis would use the binary variable for selection of the option (1 = respondent selected the option, 0 = respondent did not select the option) as the dependent variable. The independent variables would then be the binary variables used to represent the attributes (described above),11 the cost of the option, and characteristics of the respondent (age, gender, distance from site, etc.). The estimated marginal effect coefficients for the different attribute level variables in the MNL can then be divided by the negative12 of the marginal effect for the cost variable to provide an estimate of the willingness to pay for the attribute level. Comparing the estimated willingness to pay values for the attribute levels and the different attributes provides estimates of trade-offs between levels with the attribute and between attributes.
Unusual problems requiring special sampling procedures
There are no unusual problems in this effort requiring special sampling procedures.
Less frequent than annual collection
This is a one-time date collection.
3. Describe the methods used to maximize response rates and to deal with nonresponse. The accuracy and reliability of the information collected must be shown to be adequate for the intended uses. For collections based on sampling, a special justification must be provided if they will not yield "reliable" data that can be generalized to the universe studied.
NOAA expects this survey will provide sufficient data for its intended purpose. First, the results are meant to provide information on how people value trade-offs and to provide input into future restoration decisions. It is not NOAA’s intent that these results be used as the sole decision factor in making restoration decisions. The results are expected to provide indications of the relative values that people place on restoration options. Second, the data will be relevant for the areas where we are surveying. However, the results are not meant to drive decisions in the areas we are surveying. At Forsythe, the results will provide an estimate of the value of work that was performed. In Jamaica Bay, the results will provide input into the larger conversation about shoreline protection in the Bay, but will not be a primary driver of decisions in the Bay.
NOAA’s approach to maximize response begins with following good survey practices. First, as described above, NOAA will obtain a sample email list to use under this project that is representative of the U.S. population. NOAA will draw a random sample from that list and implement the survey using that sample. NOAA will send a pre-notification email, a follow-up email with the survey link, and then up to two additional reminders to each.
NOAA will have its subcontractor, ERG, perform a series of analyses and adjustments to assess and deal with potential nonresponse bias. These include:
Compare sample characteristics to population characteristics derived from archival data. The sample will contain information on gender, age, race, Hispanic origin, employment status, marital status, home ownership, education level, and household income. ERG will use statistical tests to compare each of these sample characteristics to data from the Census Bureau for the areas where we draw the sample. This analysis will allow us to determine whether the respondents to our survey are similar to those in the geographic area from which they were drawn. If the sample does not match the population characteristics, there should be some concern for nonresponse bias. However, even if the sample is not statistically different from the population on the key characteristics, this does not guarantee an unbiased sample. This simply tells us that our sample matches the population for the area we are sampling. If the sample does match, on the other hand, we can say that the sample is most likely not biased due to differences in these characteristics.
Compare the characteristics of responders to non-responders within the panel using panel profile data available from GfK. GfK maintains a large amount of data on its panel members, including gender, age, race, Hispanic origin, employment status, marital status, home ownership, education level, and household income. These data can be made available to ERG for both respondents and individuals within the panel who did not respond. ERG will use statistical tests to compare the responders to the non-responders within the panel on the characteristics listed above. Thus, ERG can assess whether the pool of respondents differs from the pool of non-respondents within the panel for the characteristics that GfK maintains. If non-responders within the panel are significantly different, we should have concerns over a biased sample.
Compare results to other studies. ERG will compile studies that have used similar methods (e.g., contingent valuation studies or choice experiments), especially in the New York and New Jersey area, for similar issues (salt marsh restoration and storm protection) and compare our estimates to those from other studies.13 There is no requirement that our estimates be equivalent to other studies, but our resulting estimates should be consistent. For example, if our sample is biased due to nonresponse and the resulting sample is comprised of people who have strong feelings for environmental protection, our estimates may be significantly larger than values from other studies. For the most part, this will be a qualitative comparison. If we identify some studies that are particularly relevant, we can compare the 95 percent confidence intervals for the resulting estimates, although we have not identified any such study to date. Another approach in this regard would to be to compare our estimates to values that could be derived from meta-analysis functions. John Loomis at Colorado State University has spent considerable time and effort developing a set of meta-analysis functions that could be used for this purpose.14 If our estimates are consistent with the values derived from meta-analyses we can have some confidence in our estimates.15 If our resulting estimates are not consistent with estimates from other studies or meta-analyses, and the inconsistencies are not explainable in the study design, we should be concerned about nonresponse bias.
Compare early to late respondents. In implementing the survey, ERG will send out an initial request for response and then follow up with reminders. ERG will compare the responses for those who responded to the first request to those who responded to later requests. The purpose of this analysis is to determine whether those who took more effort to obtain a response from (late responders) are different than those who took less effort to obtain a response from (early responders). If the late responders differ significantly in the data being provided from the early responders, then we should have some concern over nonresponse bias. Specifically, if late responders differ from early responders, it may also be the case the non-responders would also differ in the responses to the survey questions. Although similar responses from early and late responders does not guarantee unbiased data, we can have more confidence in our data if the two groups answered questions similarly.
Calculate weights reflecting non-response. Finally, ERG will adjust the sampling weights for nonresponse. Each respondent will have a sampling weight equal to the inverse of his/her probability of selection into the sample. ERG will adjust the weights using the following approach:
First, we will partition the sample into sub-groups where nonresponse appears to be an issue. For example, if we compare the sample to Census data and the GfK panel for the area and find that lower income individuals were less likely to respond, then we will use income to partition the sample.16
Second, using the GfK sample data for the relevant characteristics (e.g., income), we will formulate response probabilities for the different groups. We will be able to do this since the sample is being drawn from the GfK panel and we will know the characteristics of the non-responders. Continuing the example above, we may form 4 income groups and calculate the probability of response from each income group.
Finally, we will adjust the sampling weights by multiplying the sampling weight by the inverse of the response probability.
These adjusted weights will then be used in place of the non-adjusted weights in performing our analyses.
Finally, ERG will generate a memo that details the results of these analyses and provide that to NOAA as part of the project record. Furthermore, all reports or papers for this project will contain a section that details the results of the non-response analyses.
4. Describe any tests of procedures or methods to be undertaken. Tests are encouraged as effective means to refine collections, but if ten or more test respondents are involved OMB must give prior approval.
NOAA has pre-tested the Forsythe instrument, and in the process of pre-testing the Jamaica Bay instrument, with a limited number of individuals to refine the instrument as needed. For each instrument, NOAA asked its subcontractor ERG to pre-test the instrument with nine (or fewer) people who live the in New York and New Jersey area. For the Forsythe pre-test, ERG conducted a total of seven pre-tests and had each individual complete a paper version of the instrument and then discussed the instrument with each individual to obtain feedback on the instrument and to get ideas on how to improve the instrument. An identical process is being followed for the Jamaica Bay instrument. Based on feedback from the Forsythe pre-test, ERG implemented a number of changes to the instrument.
To develop this instrument, NOAA worked with ERG and its consultant Craig Landry at the University of Georgia. Dr. Landry is an expert at designing contingent valuation and choice experiment surveys. Furthermore, ERG and Dr. Landry started with the instrument used by Petrolia et al. (2014) as a basis for developing the instruments for this data collection.17
5. Provide the name and telephone number of individuals consulted on the statistical aspects of the design, and the name of the agency unit, contractor(s), grantee(s), or other person(s) who will actually collect and/or analyze the information for the agency.
NOAA worked with the following individuals in developing this study design and survey instrument.
Name |
Organization |
Contact information |
Lou Nadeau, Ph.D. |
Eastern Research Group, Inc. |
781-674-7316 |
Craig Landry, Ph.D. |
University of Georgia |
706-542-2481 |
Additionally, NOAA and ERG held conversations with a number regional stakeholders about this project, including Forsythe National Wildlife Refuge, USGS, The Nature Conservancy, Jamaica Bay Eco-Watchers, and the U.S. Army Corp of Engineers.
The data collection process will be managed by Eastern Research Group, Inc. (ERG).
References
Baker, Laurence, Todd H. Wagner, Sara Singer, and M. Kate Bundorf. 2003. “Use of the internet and email for health care information: Results from a national survey,” Journal of the American Medical Association 289: 2400-2406.
Baker, Laurence C., M. Kate Bundorf, Sara Singer, and Todd H. Wagner. 2003. Validity of the survey of health and the internet, and Knowledge Networks’ panel and sampling. Stanford, CA: Stanford University Press
Schlenger, William E., and Silver, R. C. 2006. Web-based methods in disaster research. In F. H. Norris, S. Galea, M. J. Friedman, & P. J. Watson (Eds.), Methods for Disaster Mental Health Research (pp. 129-140). New York: Guilford Press.
Silver, R. C., E. A. Holman, D. N. McIntosh, M. Poulin and V. Gil-Rivas. 2002. Nationwide longitudinal study of psychological responses to September 11. Journal of the American Medical Association 288(10): 1235-1244.
Heeren, T., E.M. Edwards, J.M. Dennis, S. Rodkin, R.W. Hingson, and D.L. Rosenbloom. 2008. A comparison of results from an alcohol survey of a prerecruited internet panel and the National Epidemiologic Survey on Alcohol and Related Conditions. Alcoholism: Clinical and Experimental Research 32(2): 222 - 229.
Chang, LinChiat, and Jon A. Krosnick. 2009. National surveys via RDD telephone interviewing vs. the internet: Comparing sample representativeness and response quality. Public Opinion Quarterly 73(4): 641-678.
Baker, R., S.J. Blumberg, J.M. Brick, M.P. Couper, M. Courtright, J.M. Dennis, D. Dillman, M.R. Frankel, P. Garland, R.M. Grovers, C. Kennedy, J. Krosnick, and P.J. Lavrakas. 2010. Research Synthesis: AAPOR Report on Online Panels. Public Opinion Quarterly DOI: 10.1093/poq/nfq048.
Yeager, David S., Jon A. Krosnick, LinChiat Chang, Harold S. Javitz, Matthew S. Levendusky, Alberto Simpser, and Rui Wang. 2011. Comparing the accuracy of RDD telephone surveys and internet surveys conducted with probability and nonprobability samples. Public Opinion Quarterly 75(4): 709-747.
M Boxer, JK Aronson, L Saxe, 2013. Using consumer panels to understand the characteristics of US Jewry, Contemporary Jewry 33 (1-2), 63-82.
1 https://www.gfk.com/Documents/GfK-KnowledgePanel-ESOMAR-28-Questions.pdf; the citations for the studies do not appear in the linked document above, but have been included below and can be found (along with others) in GfK’s bibliography document: http://www.knowledgenetworks.com/ganp/docs/KN-Bibliography.pdf. ERG also notes that the bibliography document contains references to valuation studies that have used the GfK sample (see page 2 of the bibliography).
2 NOAA previously used a 65 percent estimate from Gfk for this value. In recent discussion, GfK recommended using 60 percent instead.
4 Johnson, R. and Orme, B. (1996), ”How Many Questions Should You Ask In Choice-Based Conjoint Studies?” ART Forum Proceedings.
5 Orme, B. (2010), Getting Started with Conjoint Analysis: Strategies for Product Design and Pricing Research. Second Edition, Madison, Wis.: Research Publishers LLC.
6 For example, for the salt marsh restoration survey, the attributes are the amounts of the marsh restored, coastal protection, flood protection, habitat, and recreation, as well as the cost. For the coastal protection survey, the attributes are storm surge protection, flood protection, habitat, recreation, and cost.
7 Thus, since each respondent has six records and was presented with two choice sets, each respondent must have 2 records with a “yes” in the selection binary variable and 4 records with a “no.”
8 This, however, is not true for the cost variable which is treated as a quantitative value for analytical purposes.
9 In MNL regression, the yes values are converted to a one and the no values are converted to a zero.
10 As above, each record in the analysis database corresponds to one option that was presented to a respondent. Each option would have no additional home protected (“status quo”), 1,000 homes protected, 3,000 homes protected, or 6,000 homes protected.
11 One additional detail must also be accounted for; one of the binary variables for each attribute must be omitted (i.e., a “base” level) or the model would be perfectly collinear. This complicates calculation of marginal willingness to pay. However, a coding scheme exists to allow for estimation of the marginal effects of for the “base” attribute level. This is described in Holmes, Thomas P. and Wiktor L. Adomowicz, 2003. “Attribute-Based Methods,” in Champ, Patricia A., et al., eds, A Primer on Nonmarket Valuation, Springer Science+Business Media, New York, pp. 187-188.
12 The value must be multiplied by -1 for algebraic reasons.
13 One aspect we would need to assess from other studies is whether those studies also have nonresponse issues.
15 We do note, however, that the assessment usually runs in reverse. Specifically, primary studies such as ours are used to validate estimates derived from meta-analyses. Nevertheless, using the meta-analyses as a comparator may provide some insight into the potential for nonresponse bias.
16 It may be necessary to partition the sample in more than one dimension; for example, income and age.
17 Petrolia, D.R., M.G. Interis, and J. Hwang. 2014. “America's wetland? A national survey of willingness to pay for restoration of Louisiana's coastal wetlands.” Marine Resource Economics 29(1):17-37.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Modified | 0000-00-00 |
| File Created | 2021-01-25 |
© 2026 OMB.report | Privacy Policy