WIA Gold Standard Evaluation, Part B of supporting statement, 10.2.2012 Final
WIA Gold Standard Evaluation, Part B of supporting statement, 10.2.2012 Final.docx
WIA Gold Standard Follow-Up Surveys, Veterans' Study, and Cost Data
OMB: 1205-0504
WIA Gold sTANDARD fOLLOW uP AND vets
part b: collection of information
involving
statistical methods
The U.S. Department of Labor’s (DOL) Employment and Training Administration (ETA) is undertaking the Workforce Investment Act (WIA) Adult and Dislocated Worker Programs Gold Standard Evaluation (WIA Evaluation). The overall aim of this evaluation is to determine whether adult and dislocated worker services funded by Title I of WIA—currently the largest source of federal funding of employment and training services—are effective and whether their benefits exceed their costs. ETA has contracted with Mathematica Policy Research and its subcontractors—Social Policy Research Associates, MDRC, and the Corporation for a Skilled Workforce—to conduct this evaluation. The evaluation was launched in sites starting in November 2011, and all sites will begin the intake of customers into the study no later than August 2012.
An initial data collection package, approved in September 2011 (Office of Management and Budget [OMB] clearance number 1205-0482), requested clearance for a form to check the study eligibility of the customer, a customer study consent form (indicating the customer’s knowledge of the evaluation and willingness to participate) and the collection of data at baseline through a study registration form and contact information form, as well as site visit guides for the collection of qualitative information on WIA program processes, services and training.
As part of the WIA Evaluation, ETA has now authorized a supplemental study of veterans seeking employment and training assistance through the American Job Center system. The Veterans’ Supplemental Study (VSS) has two components: (1) a qualitative study examining how the system provides services to veterans and (2) a quantitative study examining the characteristics of veterans served through the American Job Center system, the services veterans receive, and their outcomes, using administrative data reported by states. These sub-studies will use data from the same 28 sites participating in the WIA Evaluation.
This second and final package requests clearance for the veterans’ data as well as two other remaining data collection efforts for the WIA Evaluation, specifically:
Two follow-up surveys conducted at 15 and 30 months after random assignment, with a sample of approximately 6,000 WIA customers included in the WIA Evaluation;
Cost data collected on three forms—a program costs questionnaire, a staff activity log, and a resource room sign-in sheet—for use in estimating the costs of WIA services received by sample members for the benefit-cost analysis; and
The aforementioned veterans’ data for the VSS, consisting of qualitative data on veterans served at the 28 local workforce investment areas (LWIAs) participating in the WIA Evaluation. For the VSS qualitative analysis, additional questions and several activities will be added to the WIA Evaluation’s second round of site visits to the 28 LWIAs. (A separate quantitative analysis will use two sets of administrative data that states already report to the DOL: the WIA Standardized Record Data [WIASRD] and Wagner-Peyser data. Because the data is already reported to the DOL, there is no additional burden associated with this quantitative data collection.)
Appendices A and B of this package present the 15- and 30-month follow-up survey instruments, respectively. Appendix C includes the advance letters, reminders, and follow-up letters that will be sent to sample members as part of the follow-up survey efforts. Appendix D presents the cost data collection package. Appendix E presents the site visit protocols for the VSS, and a short form to be completed by focus group respondents. Also for the VSS, Appendix F presents the customer consent form that will verify the veteran’s consent to participate in a focus group (organized in a portion of the LWIAs). The form also includes a consent request to have researchers review the veteran’s case file, if selected for review.
1. Respondent Universe and Sampling
a. WIA Evaluation
One of the main goals of the WIA Evaluation is to broadly generalize the findings to the national population of WIA adults and dislocated workers who are served by the program during the period covered by the evaluation. To accomplish this, a two-stage clustered design will be employed, first by randomly selecting sites and then by randomly assigning all WIA adults and dislocated workers (with a few exceptions) who reach the point of being offered intensive services.
i. Site Selection
While the overall WIA study was approved under OMB clearance number 1205-0482, it may be beneficial in understanding the current Information Collection Request to review some of the elements addressed in that earlier clearance. The WIA Evaluation will estimate the impact of intensive services and training funded by WIA adult and dislocated worker local formula funding. As this funding is administered by LWIAs, the LWIA is the sampling unit for the WIA Evaluation.
The
sample frame. To construct the sample frame for LWIA selection,
a list of all active LWIAs was assembled from the latest two years of
the WIASRD available, which were from April 2006 through March
2008. For each LWIA, these data include the annual number of adults
and dislocated customers who received WIA intensive services (some of
whom also received training) and exited the program (referred to as
“WIA exiters”). This average annual number was then
multiplied by 1.5 to represent the number of such customers who would
be served in an
18-month period. The study will include only
persons who are eligible for and seek intensive services. Thus, the
2006 to 2008 counts of WIA exiters were used to construct a sample
frame for assessing the likely flow of customers in each LWIA who
will be subject to random assignment during the 18-month sample
intake period.
In recent years, some LWIAs changed their service receipt definitions so that nearly all American Job Center customers are reported as having received intensive services, even though the intensive service received might be defined as staff-assisted core services in other areas. These definition changes resulted in large increases in reported WIA intensive service customers in some areas in recent years. For example, in Program Year (PY) 2007, New York received seven percent of all WIA formula funding, but nearly 20 percent of all WIA customers who were designated as having received intensive services or training. On the basis of this information, ETA has decided that random assignment should be conducted at the point when customers start receiving intensive services as defined by most sites. Consequently, the exact definition of “core” and “intensive” services is currently being determined after gathering detailed information on the nature and timing of WIA service offerings from each of the study sites and may differ slightly from the definitions used by the sites.
The population counts in some LWIAs were adjusted to reflect the definition of what constitutes “intensive services.” This adjustment moves the point of random assignment later in the WIA service flow process in sites that define intensive service receipt particularly early in the process. Two approaches were used for identifying these sites: (1) gathering information from the study’s advisory panel and evaluation team on LWIAs that are known to have changed their service designations, and (2) identifying large program year increases in intensive service customer counts using recent WIASRD data.
This analysis identified four areas for count adjustments: (1) three LWIAs in Texas, (2) all LWIAs in Oklahoma, (3) the “balance-of-state” LWIA in Indiana (which excludes the Indianapolis LWIA), and (4) all LWIAs in New York. Intensive service customer counts were adjusted downwards in these sites using two approaches: (1) dividing their trainee rates in the years after the definition changes by their typical trainee rates during the years prior to the changes, and (2) using the ratio of WIA funding levels to counts of intensive service customers. The first adjustment was made in all four sets of sites mentioned above. The second adjustment was made on top of the first only for the New York sites, where definitional changes began before our earliest available data, and hence, the first deflation approach alone was insufficient for estimating the number of intensive customers using a common definition. The main implication of these adjustments is that LWIA counts in New York were reduced to about 35 percent of the unadjusted counts. Smaller adjustments were made in the aforementioned sites in Texas, Oklahoma, and Indiana.
In 2006-2008, there were slightly fewer than 600 active LWIAs. The smallest sites—defined as those with fewer than 100 intensive service customers annually—were excluded from the sample frame, as well as sites outside the 48 contiguous states and the District of Columbia. The exclusion of the smallest LWIAs and those outside the U.S. mainland avoids the expenditure of substantial resources on recruiting and supporting the sites with little added to the precision of the impact estimates. Thus, the sample frame included 487 LWIAs representing more than 98 percent of the WIA population of intensive service customers in the mainland United States.
Site selection approach. WIA services vary by region, so that regional balance was a top priority in site selection. Accordingly, the evaluation team explicitly stratified by the six DOL administrative regions and selected sites within each region with probabilities proportional to the size of the site (PPS), where the size of the site was measured by the number of customers who received intensive services. The random selection of sites was conducted without replacement.
The number of LWIAs to select within each region was determined based on the regional shares of the total sample universe. This resulted in the following allocation of sites across the six regions: four sites in Region 1, three sites in Region 2, seven sites in Region 3, five sites in Region 4, seven sites in Region 5, and four sites in Region 6. These allocations reflect (1) the allocation of a “residual site” due to rounding to Region 2 which had only two sites based on their population shares, and (2) one site being added to Region 5 from Region 3 to ensure an adequate representation of large Midwest states.
The New York City LWIA and Gulf Coast Workforce Board LWIA were selected with “certainty” because they each contain a large fraction of the WIA customer population in their regions and so they had selection probabilities of greater than one.
The noncertainty sites were selected without replacement using PPS sampling within the explicit strata defined by the six DOL administrative regions. Within each region, the team implemented the PPS sampling process using systematic sampling, where sites were sorted (implicitly stratified) in order by (1) whether they are big or small (greater or less than 600 exiters annually), (2) their state, and (3) whether their training rate for the adult and dislocated worker populations (the percentage of intensive service customers who participated in a WIA-funded training program) is greater or less than 50 percent. This approach ensured a diverse set of states within each region, protected against getting many small sites by chance, and ensured a representative distribution of site-level training rates.
After sorting the sites within each region on those three characteristics and then randomly after that (using computer-generated random numbers), the team implemented PPS sampling by first “duplicating” site observations based on the site’s size measure (for example, a site with 200 customers contributed 200 observations to the ordered dataset). The team then selected a random starting number for each ordered list. The team first selected for the study the site corresponding to the starting number, and then sequentially selected every Nth site thereafter, where N depended on the desired number of sites to be selected in the region and the total number of observations in the ordered list. For example, if the ordered list for a region had 1,000 site observations, four sites were to be selected, and the 50th observation was the random starting point, then the team selected the sites corresponding to observations 50, 300, 550, and 800 (where N=250).
Using simulations to test the site selection approach. To determine the likelihood that the site selection strategy might fail to generate an adequately representative sample of sites along the desired characteristics, simulations of the site selection approach were conducted prior to sampling. Each simulation is a test run of the sampling procedure, implemented exactly as it would be for the actual selection of study sites. These simulations entailed drawing 2,000 different sets of 30 sites and examining the distribution of sites across the regions that resulted. The distribution of the training rate was also calculated each time. Table B.1 shows the results of the simulations. The second column shows the share of the population in each DOL region and the training rate in the population. The third column shows the mean share of the sample in each region and the mean training rate across the 2,000 simulations. The final three columns show the 10th, 50th, and 90th percentiles in the distributions for each region. (Because the percentiles are shown separately for each region, the columns do not reflect results for a single simulation. Thus, the percentages in each of these columns do not always sum to 100.) The final three columns also show the 10th, 50th, and 90th percentiles for the training rate.
As Table B.1 shows, the distribution of possible site characteristics closely tracks the population distribution, even when relatively low (10th percentile) or high (90th percentile) points in the distribution are considered. Simulations were also conducted for other site selection rules—including selecting sites at random without stratification, using several other stratification schemes, or using sets of sites matched prior to sampling—however, the approach described above generated the closest predicted match to the distribution of site characteristics in the full population while also maintaining a good distribution of sites across states within regions. Most importantly, this approach performed well even if the draw was “unlucky”—other approaches did well on average but were susceptible to draws that, by chance, did not mirror the population characteristics.
Table B.1. Simulated Distributions of Site Characteristics
Characteristic |
Population |
Simulated Sample Distribution |
|||
Mean |
10th
|
50th
|
90th
|
||
Percentage of Population in Administrative Region |
|
|
|
|
|
Region 1 (Boston): CT, MA, ME, NH, NJ, NY, RI, VT |
14 |
13 |
11 |
12 |
14 |
Region 2 (Philadelphia): DE, DC, MD, PA, VA, WV |
7 |
8 |
6 |
8 |
10 |
Region 3 (Atlanta): AL, FL, GA, KY, MS, NC, SC, TN |
26 |
25 |
23 |
25 |
28 |
Region 4 (Dallas): AR, CO, LA, MT, ND, NM, OK, SD, TX, UT, WY |
17 |
19 |
17 |
19 |
21 |
Region 5 (Chicago): IA, IL, IN, KS, MI, MN, MO, NE, OH, WI |
21 |
21 |
19 |
21 |
23 |
Region 6 (San Francisco): AZ, CA, ID, NV, OR, WA |
14 |
14 |
12 |
14 |
16 |
Percentage of Those Who Request Intensive Services Who Receive Training |
57 |
55 |
50 |
55 |
59 |
Source: WIA Standardized Record Data for adult and dislocated worker exiters between April 2006 and March 2008 projected to 18 months.
Note: Characteristics are weighted by sample size at selected sites.
The selected sites. Table B.2 shows the 30 selected sites, by region. The sample is balanced across regions and has a mix of sites that are large and small and that have high and low training rates. The 30 sites are spread across LWIAs from 21 states, and the sample has 16 sites from the eight states with the largest WIA funding levels (in PY07), including at least one site in each of those eight states. Seventeen of the 30 sites are large (greater than 600 customers annually) and 18 have a high training rate (greater than 50 percent).
Table B.2. LWIA Sites Selected for Evaluation
Region |
State |
Size |
Training Rate |
Site Name |
1 |
NJ |
Small |
Low |
Essex County Workforce Investment Board |
1 |
NY |
Large |
Low |
New York City |
1 |
NY |
Large |
Low |
Albany/Rensselaer/Schenectady Counties |
1 |
NY |
Small |
High |
Chautauqua County |
2 |
PA |
Large |
Low |
Central Pennsylvania Workforce Development Corp. |
2 |
PA |
Small |
Low |
Southwest Corner Workforce Investment Board |
2 |
PA |
Small |
Low |
Northwest Workforce Investment Board |
3 |
FL |
Large |
High |
Region 8, First Coast Workforce Investment Board |
3 |
GA |
Small |
High |
Atlanta Regional (Area 7) |
3 |
KY |
Large |
Low |
Kentuckiana Works |
3 |
MS |
Large |
High |
Twin Districts Workforce Investment Area |
3 |
SC |
Large |
Low |
Lower Savannah Council of Governments |
3 |
SC |
Small |
High |
Santee Lynches Regional Council of Governments |
3 |
TN |
Large |
High |
East Tennessee Human Resource Agency |
4 |
LA |
Small |
High |
Orleans Parish |
4 |
SD |
Large |
Low |
South Dakota Consortium |
4 |
TX |
Large |
Low |
Gulf Coast Workforce Board-The WorkSource |
4 |
TX |
Large |
High |
North Central Texas Workforce Development Board |
4 |
TX |
Small |
High |
South Plains Workforce Development Board |
5 |
IL |
Small |
High |
Du Page County Workforce Investment Board |
5 |
IN |
Large |
Low |
Indianapolis Private Industry Council |
5 |
MI |
Large |
High |
Thumb Area Michigan Works! |
5 |
MI |
Small |
High |
Muskegon County Department of Employment and Training |
5 |
MO |
Small |
High |
Central Region |
5 |
OH |
Large |
High |
WIA Area 7 |
5 |
WI |
Small |
High |
WOW Workforce Development Inc. |
6 |
CA |
Large |
Low |
Fresno County Workforce Investment Board |
6 |
CA |
Large |
High |
Sacramento Employment & Training Agency |
6 |
NV |
Small |
High |
Nevadaworks |
6 |
WA |
Large |
High |
Workforce Development Council of Seattle-King County |
Note: “Small” sites are those with fewer than 600 customers annually, and “large” sites are those with 600 or more annually. “High” and “Low” training rate categorization is based on whether the site’s training rate is greater or less than 50 percent.
Recruiting sites. Recruitment activities included letters and calls from the Assistant Secretary of ETA and multiple visits from the evaluators to explain the study. While these visits involved lengthy discussions about the evaluation with senior staff and members of the workforce investment boards, no data were collected during those visits and no WIA customers were contacted.
Following a review of Section 172 of the WIA and queries to staff in the Department’s Solicitor’s Office, ETA concluded that the Department does not have statutory authority to require local workforce investment areas (LWIAs) to participate in the evaluation. Although Section 172 requires the Secretary to “provide for the continuing evaluation of the programs and activities” and directs the Secretary to “conduct as (sic) least 1 multisite control group evaluation,” there are no provisions regarding participation in these evaluations by any organization(s). This includes those receiving Federal funding for WIA programs or for providing services to WIA participants.
All but four of the 30 sites that were originally selected (and listed in Table B.2) have agreed to participate in the evaluation. Thus 26 of the 30 sites—or 87 percent of the sites, representing 89 percent of the customers in the 30 sites—agreed to participate. The sites that declined to participate in the study were (1) WIA Area 7 in Ohio, (2) Thumb Area Michigan Works!, (3) DuPage County, Illinois, and (4) Nevadaworks. These sites are highlighted in Table B.2.
Accounting for sites that choose not to participate. Because the 26 sites that agreed to participate may differ from the four sites that refused to participate in ways that affect the magnitude of the impacts, a potential exists for a bias in the impact estimates. Hence, we will conduct a comprehensive sensitivity analysis to address potential nonresponse biases on the impact estimates due to the noncooperation of some sites.
We propose two approaches for dealing with nonresponse. Our primary approach for assessing the sensitivity of our impact findings to site nonparticipation calls for the selection of “matched replacement” sites for each of the four sites that refused to participate (referred to as “refuser” sites). As discussed further below, for each refuser site, we selected the most closely matched replacement sites based on the stratification variables discussed above. Impacts in the replacement sites could differ from those in the initially-selected refuser sites. However, the replacement sites matched well to the refuser sites based on the observable matching data (see below), and thus, form a reasonable alternative approach for “imputing” missing impact data for customers in the refuser sites. This approach also has the potential for increasing the precision of the impact estimates by increasing the number of study sites. Finally, the inclusion of additional “matched” sites will allow the evaluation to obtain more precise estimates of specific program features, which is an important evaluation objective.
The secondary approach will be to statistically adjust for site nonparticipation using information on the characteristics of the 26 sites that agreed to participate and the four sites that refused. As discussed in more detail below in Subsection 2c, this approach will involve adjusting the sample weights for nonresponse using propensity score methods and using multiple imputation methods.
Selection of replacement sites. Replacement sites were selected to be as similar as possible to the refusing sites using the stratification variables discussed above. To do this, when the sites were selected, ordered lists of five replacement sites were also developed for each site. Replacements were chosen by searching for sites that were of similar size, in the same region, in the same state, and had similar training rates as the originally-selected site. The criteria were prioritized in the order listed. The size of the site was considered the most important feature to match on to ensure sample size targets could be met without drastically changing the rates at which customers were assigned to the restricted services groups.
Importantly, this selection procedure for the replacement sites is similar in spirit to a simple stratification approach that would have called for the allocation and random selection of replacement sites within strata. Our approach is an extreme form of stratification where replacement sites were matched to original sites using the stratification variables. Under either stratification approach, the inclusion of replacement sites in the analysis sample could yield unbiased estimates to the extent that site nonresponse is independent of impacts within the strata. In this case, it is effectively random whether the original or replacement sites were selected “first.”
The main advantage of our stratification approach is that it is more likely to yield replacement and original sites that are better balanced on the stratification variables, especially due to small sample sizes. The analogy of our approach in randomized control trial sampling is the use of propensity scoring to first pairwise match sampling units prior to random assignment and then to select one of each pair to the treatment or control group (see, for example, Murray 1998 and Schochet 2008a) or to use minimization to achieve balance for treatment assignments within strata (see, for example, Pocock 1983).
In essence, our replacement site selection strategy used a “model” that minimized differences between the original and replacement sites using the stratification variables that were available at the time of sampling. The replacement sites were selected at the same time as the original sites due to the considerable amount of uncertainty as to when the original sites would make their participation decisions. Thus, in order to obtain a timely sample, we often contacted replacement sites before the original sites made their final decisions.
Recruitment of Replacement Sites. We recruited two replacement sites. The first replacement site for Thumb Area Michigan Works!—Southeast Michigan—agreed to participate. We were required to go to the second replacement site for WIA Area 7 in Ohio—Chicago Workforce Investment Council. The two other sites that declined—DuPage County and Nevadaworks—declined to participate later in the study and have not yet been replaced. Because of the lateness of their decisions, they will not be replaced. Table B.3 summarizes our recruitment success.
Table B.3. Success at Site Recruitment as of June 2011
Selected to Participate/Agreed to Participate |
Number
|
Number
of Customers Who Receive |
Sites selected originally to participate in the study |
30 |
68,130 |
Agreed to participatea |
26 |
60,811 |
Did not agree to participate |
4 |
7,319 |
Replacement sites agreed to participateb |
2 |
4,424 |
Replacement site did not agree to participateb |
1 |
8,937 |
All sites that agreed to participate in the study |
28 |
65,235 |
aThe primary analysis sample.
bThe second replacement site was used to replace one site that refused.
Our primary analysis will include 28 sites—the 26 sites that were originally selected and have agreed to participate in the evaluation and the two replacement sites. An important reason for including the two replacement sites in the study is that three of the four refuser sites were from the Midwest Region; only four of the seven original sites in this region remain in the 26-site sample. Standard nonresponse adjustments could be applied to adjust for this serious underrepresentation of the WIA population in the large Midwest Region (for example, by giving larger weights to the four sites in this region that are in the 26-site sample). However, another approach to adjust for this potential site-level nonresponse is to include in the sensitivity analysis the two replacement sites that are both in the Midwest Region.
Table B.4 compares the characteristics of the original 26-site samples with the 30- and 28-site samples using the stratification variables used for sampling. The two replacement sites are from the same Midwest region as the two refuser sites and one is in the same state as the site it is replacing. The replacement sites are of similar size to the attrited sites (about 3,000 customers). The training rate is somewhat lower in the replacement sites than their two matched original sites, however, because a lower priority was placed on the training rate in the matching than on the region and size variables. It is interesting, however, that the training rate in the two replacement sites are similar to the overall training rate in the 30- and 26-site samples.
Table B.4. Stratum Characteristics of Sites in Different Samples
Characteristic |
Original |
Post-Attrition |
Attrited Sites |
Replaced Sites |
Replacement Sites |
Post-Replacement Sites |
Number of Sites |
30 |
26 |
4 |
2 |
2 |
28 |
Region |
|
|
|
|
|
|
1 |
13.3% |
15.4% |
0 |
0 |
0 |
14.3% |
2 |
10.0 |
11.5 |
0 |
0 |
0 |
10.7 |
3 |
23.3 |
26.9 |
0 |
0 |
0 |
25.0 |
4 |
16.7 |
19.2 |
0 |
0 |
0 |
17.9 |
5 (Midwest) |
23.3 |
15.4 |
75 |
100 |
100 |
21.4 |
6 |
13.3 |
11.5 |
25 |
0 |
0 |
10.7 |
Size Stratum |
|
|
|
|
|
|
1 |
10.0% |
11.5% |
0 |
0 |
0 |
10.7% |
2 |
33.3 |
30.8 |
50 |
0 |
0 |
28.6 |
3 |
26.7 |
26.9 |
25 |
50 |
50 |
28.6 |
4 |
10.0 |
11.5 |
0 |
0 |
0 |
10.7 |
5 |
6.7 |
7.7 |
0 |
0 |
0 |
7.1 |
6 |
10.0 |
7.7 |
25 |
50 |
50 |
10.7 |
7 |
3.3 |
3.8 |
0 |
0 |
0 |
3.6 |
Average Number of Customers |
2,271 |
2,339 |
1,830 |
2,878 |
3,066 |
2,391 |
Percent in Training |
55.9 |
52.7 |
76.5 |
74.5 |
55.5 |
52.9 |
We will conduct a sensitivity analysis for the inclusion of the replacement sites. Before using these two replacement sites in the analysis, we will compare the impacts in the two replacement sites with the impacts in the four original Midwest sites to examine whether the impacts in the replacement sites are atypical, and conduct F-tests to gauge whether the differences in the impacts are statistically significant. We will also use F-tests to compare the 26- and 28-site impact findings. To the extent that they provide different results, the two sets of results could suggest some selection bias due to the inclusion of the 2 replacement sites. For both the 26- and 28-site samples, we will employ statistical adjustments for site nonparticipation (see Subsection 2c).
We also will use WIASRD and Area Resource File (ARF) data to compare the final set of study LWIAs to the 30 randomly selected and to all LWIAs nationwide. (ARF data are collected by the Health Resources and Services Administration and contain detailed information on local area characteristics by county.) This comparison can be used to check the extent to which the sites resemble the LWIAs nationwide on observable characteristics. The WIASRD and ARF data will also be used to adjust the weights for site nonresponse and to perform multiple imputations.
To the extent that these adjustment methods do not fully capture unobservable differences between site responders and nonresponders that are correlated with study impacts, the impacts estimated in this study are biased estimates of the impact of the program nationwide. However, the estimates are still unbiased estimates of the impacts of the program in the sites that participated in the study.
ii. Selection of Individuals Within Sites
At each site, nearly all consenting WIA adult and dislocated worker customers who would, in the absence of the study, be offered intensive services will be randomly assigned into one of three research groups just before they would have been offered intensive services. The three research groups are the (1) full-WIA group—customers in this group can receive any WIA services and training for which they are eligible; (2) core-and-intensive group—customers in this group can receive any WIA services for which they are eligible but not training; and (3) core group—customers in this group can receive only WIA core services and no WIA intensive services or training. Thus, this evaluation is examining the impacts of WIA intensive services and training on customers’ outcomes relative to a situation in which customers have access to WIA core services only.
In selecting a point of random assignment, we considered the following criteria: (1) the point must allow customers to receive core services; (2) the point must allow us to address a meaningful research question and the intervention studied must be sufficiently large for us to expect to be able to detect its impacts; (3) the point must be at a similar point in the service flow in each site so we are addressing the same research question in each site; and (4) random assignment at this point must be operationally feasible.
Selecting the point of random assignment was challenging in this study because the sites differed in their service provision and in their definitions of intensive services. For example, some sites include nearly all staff-customer interactions as intensive services while others include only substantial interviews with employment counselors. Our approach is to define intensive services as services that require “substantial” staff input irrespective of how it is defined by the site.
While many people who use the American Job Center receive only core services, we are not evaluating core services because (1) few sites would agree to turn a customer away from the American Job Center without the offer of some service; (2) the services are typically co-funded by the Employment Service; (3) some services are accessed on-line making it difficult to deny the services; and (4) the impact of these light-touch services is likely to be too small to detect with the sample size feasible for such study. Hence, we are only evaluating the impact of “intensive” services as defined above and training.
We worked with each site to define substantial intensive services. Site staff helped to define the point of random assignment based on their understanding that the study is attempting to apply a uniform definition of intensive services and training across sites (to the extent possible).
While the terms core, intensive, and training are clear in the legislation and discussed by policy makers, frontline staff are often unaware of the terms and rarely use the term “intensive” services. In our training of staff, we will be careful to describe the point of random assignment in terms of the names staff use for services rather than “intensive” services. This will prevent any confusion with the different definitions of the terms “intensive” service. We are not asking sites to make any changes to how they record the receipt of services in their management information systems. To conduct random assignment, WIA intake counselors will input key identifying information on each customer in the study universe into a web-based computer system that will be developed by the evaluation team. The web-based system will return random assignment results within seconds. These results will be obtained using pre-programmed randomly-generated strings of random assignment statuses. The string length will depend on the sampling rates to the core-and-intensive (CI) and the core groups (C), and one CI and one C code will be randomly ordered (using computer-generated random numbers) within each string. This process will ensure that the selection of the restricted services groups will be evenly spread out over the sample intake period.
Administrative records data—including unemployment insurance (UI) records and state or local WIA management information systems (MIS) data—will be collected for the full research sample. However, as discussed later, follow-up surveys will be conducted only for random subsets of the full research sample using computer-generated random numbers within explicit strata to ensure a balanced survey sample in terms of key population characteristics. To attain a sufficient sample size, the sample intake period will span 18 months. Based on recent data, it is estimated that during an 18-month period, the participating evaluation sites would offer intensive services to about 65,000 adult and dislocated workers. Thus, we expect that about 65,000 people will go through the random assignment process.
Research group assignment rates. Only a small proportion of customers—2,000 total—will be assigned to the core group. Similarly, only 2,000 customers will be assigned to the core-and-intensive group. This leaves approximately 61,000 customers in the full-WIA group. Although an alternative approach that uses research groups of equal size would yield more statistical efficiency, this approach would also lead to large numbers of customers in the research groups who do not have full access to WIA services. Keeping the rates of assignment to these groups low is important so as not to change program operations and to be more acceptable to the sites. The planned approach, which involves restricting access to the full set of WIA services to a small portion of the customers in the study, will provide sufficient statistical power for the impact analysis (as shown by the minimum detectable impacts shown in response to question 2 below), and is likely to foster sites’ cooperation in the study.
Assignment rates to the restricted-service groups that will not have access to full-WIA services will differ by the size of the site; the rates will be lower in larger sites than in smaller sites. This is necessary to ensure that the customer sample will not consist mainly of individuals from the largest sites. The sampling rate for each of the restricted-services groups—the core group and the core-and-intensive group—will be eight percent in the smaller sites and 0.7 to five percent in the larger sites (Table B.5). By design, the sample will be close to “self-weighting.” Smaller sites are less likely to be selected under PPS sampling, but conditional on the site being selected, a higher proportion of customers will be included in the research sample, such that any given customer in the WIA population is close to equally likely to be selected into the research study. The sample will be largely self-weighting both within and across regions. However, the analysis will use sampling weights to correct for any imbalances arising if selected sites represent a smaller or larger proportion of the expected sample than they would of the population.
Sampling for the surveys. Because some important outcomes are not available from administrative sources, two follow-up surveys will be conducted with 6,000 customers. The surveys will collect a rich amount of information on sample members’ training, training program characteristics and employment and self-sufficiency outcomes.
Table B.5. Research Assignment Rates in the 28 Study Sites, by Annual Site Size
|
Sampling Rates (Percentages) |
||||
Research Group |
7,000 or More Customers |
3,000 to 6,999 Customers |
1,800 to 2,999 Customers |
900 to 1,799 Customers |
100 to 899 Customers |
Core group |
0.7 |
1.5 |
3.0 |
5.0 |
8.0 |
Core-and-intensive group |
0.7 |
1.5 |
3.0 |
5.0 |
8.0 |
Full-WIA group |
98.6 |
97.0 |
94.0 |
90.0 |
84.0 |
Source: WIA Standardized Record Data for average annual adult and dislocated worker who received intensive services and exited the program between April 2006 and March 2008, extrapolated to 18 months.
All adult and dislocated workers randomly assigned to the core-and-intensive or core groups will be included in the survey sample. However, only a random subset of 2,000 full-WIA group members will be included. Thus, the survey sample will be balanced across the three research groups, with 2,000 people in each of the three groups, yielding more precise impact estimates than would other allocations of the 6,000 customers. The random selection of full-WIA members for the survey sample will be stratified by site; within each site, the survey sample size of full-WIA members will be the same as the sample sizes for the core-and-intensive and core groups. Stratification on other characteristics will be performed to ensure that the sample is balanced in terms of adult/dislocated worker status, sex, and race/ethnicity and is well matched to the core and core-and-intensive services groups on these dimensions.
The matching approach was also considered. Such an approach would yield better balance between the survey samples. However, there are two main drawbacks. First, because there are three research groups, it will be operationally difficult to match the full-WIA (FW) group to both the CI and C groups. This can be done by, for example, (1) estimating a multinomial logit model that regresses the dependent variable (1 = FW, 2 = CI, 3 = C) on the matching variables, (2) calculating propensity scores, and (3) obtaining the matched FW group by minimizing the average distance between the FW propensity scores and those of the CI and C groups (or using another loss function). However, it is not clear that the complexity of this procedure is worth the benefits, especially since the CI and C survey samples will not be matched to each other. The second, and perhaps more important drawback, is that standard error calculations using the matching approach are less developed and transparent than under the stratified random sampling approach. This is especially true given the clustered design.
We will use the stratification approach for two reasons. First, although the stratification approach may not achieve the same level of balance as the matching approach, it will likely yield sufficiently balanced samples due to relatively large study samples and random sampling. And, we will regression-adjust the impact estimates in the analysis to account for any residual imbalances between the survey samples due to randomization. Second, the standard error calculations using this approach have been well established.
Sample attrition and response rates. The first potential source of attrition is the refusal of sites to participate (Table B.6). As discussed above, 26 out of the 30 initially-selected sites agreed to participate. The participation rate in terms of individuals is 89 percent (first row of Table B.6).
Table B.6. Assumptions About Sample Attrition in the WIA Evaluation
1. Proportion of all customers in the 30 initially-selected sites that are in the 26 sites that agreed to participate |
89% |
2. Proportion of all customers in the 26 participating sites who consent to participate in the study |
98% |
3. Proportion of consenting customers who respond to each follow-up survey |
82% |
4. Proportion of all customers (both consenting and nonconsenting) in the 30 sites who respond to each follow-up survey |
72% |
5. Proportion of all consenting customers for whom we receive administrative data |
100% |
6. Proportion of all customers (both consenting and nonconsenting) in the 30 sites for whom we receive administrative data |
87% |
7. Proportion of consenting customers who respond to both follow-up surveys |
74% |
The second potential source of attrition from the sample of customers in the participating sites occurs in obtaining consent to participate in the study (Table B.6). We expect that a high percentage of customers will agree to participate in the study. While exact numbers from other random assignment studies are unavailable, we have been told by evaluation site staff in studies of Job Corps (Schochet et al. 2003), individual training accounts (McConnell et al. 2006), National Supported Work (MDRC 1980), and a relationship skills training program (Dion et al. 2006) that refusing consent is rare. (In this study, the number of customers who refuse to participate in the study is being tracked by the Eligibility Checklist). We assume that 98 percent of all customers will agree to participate in the study (second row of Table B.6).
The third source of attrition is nonresponse to the follow-up surveys (Table B.6). We expect to receive an 82 percent response rate to each follow-up survey (third row of Table B.6). With similar adults in the 15-month follow-up for the ITA Experiment, Mathematica achieved an 82 percent response rate in a telephone survey (McConnell et al. 2006).1 We expect that 74 percent of consenting customers will respond to both surveys (seventh row of Table B.6). (We discuss our approach to obtaining a high response rate in the follow-up surveys in Section 3 that follows.)
The fourth row in Table B.6 shows the percentage of all customers (both consenters and nonconsenters) in the 30 initially randomly selected sites who we expect to respond to each follow-up survey. It is calculated as the response rate (82 percent) times the percentage of customers who consent to the study in each site (98 percent) times the percentage of customers in the 30 sites who are located in the 26 participating sites (89 percent). Sample attrition in the traditional sense will not occur in the collection of the UI wage records (Table B.6) because of the interpretation of nonmatching records. We will send the social security numbers of all participants in our study to the participating state UI agencies. The agency will match the social security numbers with their records. If they find a match, they will return the information about earnings for the quarter on that study participant. If they do not find a match, we will assume that the study participant was not employed and had no earnings in that quarter. Hence, we will have information for every study participant (fifth row of Table B.6). The sixth row in Table B.6 shows the percentage of all customers (both consenters and nonconsenters) in the 30 initially randomly selected sites for whom we expect to receive administrative data.
We recognize, however, that the information obtained from UI records could be incorrect. They could be incorrect for several reasons including: (1) the study participant’s earnings are not covered by the system (because for example, the participant is self-employed, an independent contractor, or a federal government worker); (2) the study participant works in a state not included in the study; (3) the employer incorrectly reports the participant’s earnings (employers have an incentive to under-report the amount of reported earnings because they affect the payroll tax); or (4) the study participant has given an incorrect social security number. Despite the potential concerns with these data, we propose to collect them because when reported, the amount of earnings may be more accurate and there is the potential to collect data for a longer follow-up period without additional burden to the study participants.
b. Veterans’ Supplemental Study
i. Site Selection
The VSS will include all 28 sites that were selected for and are participating in the WIA Evaluation. A detailed description of the selection process is described above.
Additional data collection—focus groups with veterans and case file reviews—are planned for eight LWIAs. These eight sites will be selected from among the 28 LWIAs participating in the WIA Evaluation. They will be purposively selected based on two factors—the size of the LWIA’s veteran population and information about a site’s promising or innovative practices. The most recent WIASRD data will be used to assess the size of each LWIA’s veteran population; those with the largest numbers of veterans served will be selected. However, as this study is also interested in learning about unique service-delivery practices, we also will seek to identify sites among the 28 that may be using such practices. Our main source of information will be the WIA Evaluation’s liaisons, who will have in-depth knowledge about their sites as a result of their regular communications with sites and their first-round visits. We also will solicit input from other sources, including VETS staff, the state veteran coordinators, and available literature. Using both these factors, we will purposively select the eight sites for additional activities so that the set includes both those serving large numbers of veterans and those implementing innovative service approaches.
The purpose of selecting these eight sites is to illuminate the experiences of veterans in the American Job Center system. Results from the data collected from veterans at these sites will not be generalizable to all LWIAs. However, they will provide useful descriptions of the types of successes, challenges, and innovations that are occurring in selected sites that can have relevance to a broader set of LWIAs.
ii. American Job Center Staff Serving Veterans and Veterans in Focus Groups for the VSS
For each LWIA, a range of staff members who are involved in various aspects of customer interaction, service provision, management, and supervision will be interviewed. They will be selected largely based on their positions and roles, so that a wide range of experiences may be probed. Some will be staff already selected for participation in the second-round implementation study visits of the WIA Evaluation, while others, such as Disability Veterans’ Outreach Program (DVOP) specialists and Local Veterans’ Employment Representatives (LVERs) specialists, will be specially chosen for this supplement.
Focus group participants will be a convenience sample of veterans who have received services recently and who are willing to participate. We will provide the designated American Job Center staff member with text to email to veterans who have received services in the past six months. The email will briefly describe the nature of the study as well as when and where the focus group will be conducted, and will ask willing participants to contact the designated staff member. That staff member will compile a list of the volunteers and some characteristics needed to select a diverse focus group, such as gender, presence of a service-connected disability, year of discharge, and job market prospects. The site visit team will then work with the designated staff member to select focus group members to recruit and the staff member will contact the selected individuals. If we are unable to convene a focus group in one of the sites, we will attempt to talk individually with up to three veterans from that site in person or by telephone, to gain some insight into veterans’ experiences.
From among the veteran customers who consent to participate in the focus groups, we will select three for a case file review. These cases will again represent a range of backgrounds and experiences, such as a mix of male and female veterans, pre- and post-9/11 veterans, and veterans with and without a service-connected disability.
Participants of these focus groups and case reviews are not intended to be representative of experiences of all veterans within a site, and are subject to bias by staff recruiting participants and by veterans themselves in deciding to participate. The data collection is intended to capture a potential range of experiences within the American Job Center system to identify themes in successes, challenges, and improvements that could be made.
c. Unusual Problems Requiring Specialized Sampling Procedures
There are no unusual problems requiring specialized sampling procedures for either the WIA Evaluation or the WIA Evaluation’s VSS.
d. Periodic Cycles to Reduce Burden
The follow-up surveys are conducted twice, at 15- and 30-months after study intake and random assignment to maximize the length of the period in which we can analyze impacts, while also maximizing recall to enhance data quality and reducing the time burden on respondents for each survey. The collection of data on program costs to support the benefit-cost analysis will occur only once. For the VSS, the interviews with staff serving veterans and the focus groups among veterans served by American Job Centers are also conducted only once.
2. Analysis Methods and Degree of Accuracy
a. WIA Evaluation’s Analysis Methods for Impact Estimation
The WIA Evaluation will estimate impacts using a finite-population, design-based approach. Accordingly, study inferences will be generalized to the WIA customer universe from which the research groups will be selected (not to a “superpopulation” of WIA programs and customers). We adopt this approach because WIA services, customer populations, and the local area context (such as unemployment rates) change somewhat over time; thus, policymakers can assess whether the evaluation findings for the full sample and key subgroups pertain more broadly to program superpopulations. The estimated variances of the impacts under this approach will be adjusted for design effects due to clustering and weighting.
The central feature of the evaluation is the random assignment of WIA customers who are eligible to receive intensive services to one of three research groups within each study site. Experimental statistical methods will yield unbiased estimates of the net impacts of WIA as it operates during the study period. For adults and dislocated workers, the net impacts of each WIA service tier can be estimated by comparing outcomes of the (1) full-WIA treatment group and the core-and-intensive group, (2) the full-WIA group and the core group, and (3) the core-and-intensive group and the core group. Impacts will be estimated not only for the full sample, but also for important subgroups defined by customer, program, and site characteristics.
i. Estimating Impacts for the Full Sample
With a random assignment design, there should be no systematic observable or unobservable differences between research groups except for the services offered after random assignment. Thus, for each customer population (adults, dislocated workers, or both combined), simple differences in the mean values of outcomes between customers assigned to any two research groups will yield unbiased impact estimates of program impacts, and the associated t-tests (adjusted appropriately for design effects due to weighting and clustering) can be used to assess statistical significance.
The study will also use regression estimators to control for residual differences between the treatment and comparison groups and to construct more efficient estimators than the simple difference-in-means estimators. The next sections discuss the variance formulas for these impact estimators under a design-based approach that will be employed for the study.
Differences-in-means estimators. The design for the evaluation is a two-stage stratified design, where nh sites (referred to as primary sampling units, or PSUs) were selected within region h with probabilities proportional to size, and mhig customers from region-h site-i will then be randomly assigned to research group g with the site-specific assignment probabilities discussed above. As discussed, site sample sizes will be selected to yield a sample that is largely self-weighting (but not completely), and there will be no poststratification. Thus, weights for customer j, denoted, by whij will be used to correct for the sample design and for site and survey nonresponse as discussed below.
Under
this design, the simple differences-in-means impact estimate for
comparing two research groups ( and
and
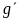 ) to
each other for a continuous or binary outcome, y, will be
calculated as follows:
) to
each other for a continuous or binary outcome, y, will be
calculated as follows:
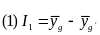
where:
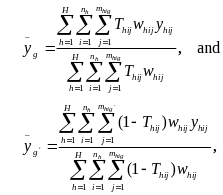
where Thij is a binary variable equal to 1
for customers in group
 and 0
for customers in group
and 0
for customers in group
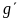 .
.
The study will use the Taylor linearization method to calculate the variance of I1. To highlight the features of this method, suppose that we are interested in estimating the variance of a population parameter =F(x1,x2,…,xn), where F(.) is a nonlinear function of the observed data vector x. Suppose next that we perform a Taylor expansion of around (1,2 ,…, n) where p= E(xp), where the E(.) operator is the expected value of xp averaging over repeated sampling from the sample universe. This Taylor expansion yields the following expression for the variance of :

Consequently, to estimate the variance of , the linearized covariates, Zi, can be used in formulas for calculating variances for population totals under clustered designs.
To
apply this method for the impact estimator in equation (1), we note
that the mean outcomes for the two research groups in equation (1)
are ratios of two sums (denoted by
 and
and
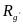 ,
respectively). Thus, using equation (2), the corresponding
linearized variables for these ratio estimators can be expressed as
follows:
,
respectively). Thus, using equation (2), the corresponding
linearized variables for these ratio estimators can be expressed as
follows:
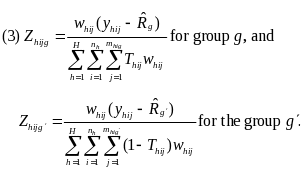
As discussed next, the way in which the study will use these linearized Z variables in the variance calculations will differ for those in the certainty and noncertainty sites.
Certainty sites. As discussed in Section 1a of Part B, two sites were selected with certainty (because these sites had selection probabilities greater than one). The customer samples in each of these sites can be treated as a simple random sample from each site. This is because the certainty sites were not “sampled,” and hence, each certainty site is effectively its own stratum. Consequently, the variance of the impact estimates in the certainty sites do not need to account for between-site variability but only within-site variability.
The study will estimate the variance of the impact estimates in the certainty sites as follows:

and where fi is the sampling fraction in site i. It is important to note that, for simplicity, the formulas are not indexed by “certainty,” although this index is implied, because these calculations will be performed using data on only those customers in the certainty sites. This convention is followed for the remainder of this section.
Noncertainty sites. The variance of the impact estimates in the noncertainty sites must account for clustering due to the sampling of sites. A key feature of these variance calculations is that the research groups are selected from the same sites, thereby creating a potential correlation between the mean outcomes of customers across the research groups.
The formulas that the study will use to calculate the variance of the impact estimates in the noncertainty sites will differ depending on whether it is assumed that the sampling of sites was performed with replacement (WR) or without replacement (WOR). Under the WR assumption, the variance formula is very simple:
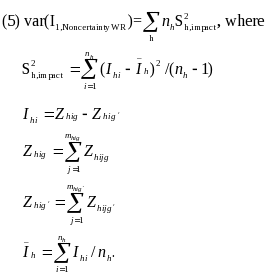
This variance expression represents the extent to which estimated impacts vary across sites (and thus, accounts for the covariance between the mean outcomes of the research groups within the same site).
One problem with the WR assumption is that it is likely to produce conservative variance estimates because it does not incorporate the finite sample correction at the site level. One way to adjust for this problem is to include the finite population correction in the variance expression in equation (5) as follows:
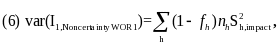
where fh represents the sampling rate in stratum h. This approach is the formula for a WOR design where PSUs (sites) are sampled with equal probabilities within each stratum (region), and where second-stage sampling rates are small (which will be the case for the evaluation).
Another approach is to assume WOR sampling with unequal first-stage state selection probabilities and to use the Yates-Grundy-Sen variance estimator:
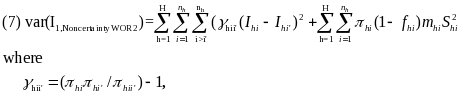
hi are state selection probabilities, and hii’ are joint inclusion probabilities for each pair of sites in the stratum. This method is somewhat cumbersome, because of the large number of joint inclusion probabilities that need to be calculated. Thus, the study will explore using this approach, but will rely more on the methods shown in equations (5) and (6).
Combined variance estimates. The study will calculate overall variance estimates by combining the variance estimates from the certainty and noncertainty sites as follows:
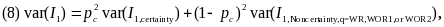
where pc is the population share in the certainty sites.
Test statistics. To assess the statistical significance of the impact estimates, the study will compute t-tests by dividing the estimated impacts in equation (1) by the square root of estimated variances from equation (8). The number of degrees of freedom for these tests will be approximated as the number of sites in the sample minus the number of strata minus 1.
ii. Regression Estimators
To obtain regression-adjusted impact estimates, the study will estimate variants of the following regression (ANCOVA) model:
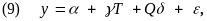
where y is an outcome variable at a specific time point, T
is an indicator variable equal to 1 for customers in group g
and 0 for customers in group
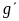 , Q
are baseline explanatory variables that are associated with key
outcome measures,
is a mean zero disturbance term, and ,
, and
are parameters to be estimated. The estimate of
represents the regression-adjusted impact estimate of WIA on the
outcome variable, and the associated t-statistic can be used to gauge
the statistical significance of the impact estimate.
, Q
are baseline explanatory variables that are associated with key
outcome measures,
is a mean zero disturbance term, and ,
, and
are parameters to be estimated. The estimate of
represents the regression-adjusted impact estimate of WIA on the
outcome variable, and the associated t-statistic can be used to gauge
the statistical significance of the impact estimate.
The study will use generalized linear model methods to estimate regression-adjusted impacts and their variances to account for the sample design. These methods generalize the Taylor series linearization method discussed above for parameters that are defined as implicit functions of linear statistics or estimating equations. These methods can be used to estimate linear models for continuous outcome measures as well as nonlinear logistic models for binary outcomes (the two main types of outcomes for which impacts will be estimated in the evaluation).
The theoretical assumptions for generalized linear models are as follows:


and g is a link function such that:

Note that the X variables in equation (12) contain both the T and Q variables in equation (9), and that the kx1 parameter vector contains both the and parameters.
The estimating equations for the exponential family of distributions (of which linear and logistic regressions are special cases) can be derived by setting to zero the derivatives of the log likelihood function with respect to . These estimating equations can be expressed as follows:
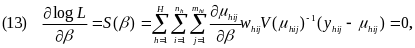
where S() is the score function.
Estimates of in equation (13) can be obtained using Newton-Raphson (Taylor Series) methods. The variance of these estimates can be calculated as follows:

where J0 is a k-by-k matrix of derivatives of the score function with respect to , and Var[S()] is the design-based variance of the score function.
An estimate of Var[S()] can be obtained using the Taylor linearization method discussed in the previous section. This is because the score function is a sum of linearized kx1 Z vectors, where the Z vector for each individual is of the form:
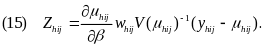
Consequently, similar procedures to those described in the previous section for the differences-in-means estimators can be used to compute Var[S()] using the linearized Z vectors. For instance, under the WR assumption, the variance estimate in the noncertainty sites can be computed as follows:
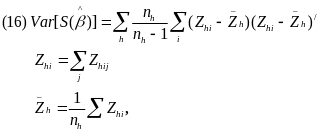
and under the WOR assumption with equal state sampling probabilities, the variance estimate can be obtained by multiplying equation (16) by (1-fh).
Linear and logistic regression procedures are special cases of the above generalized linear model formulation. For linear regression, the parameters can be estimated using the following weighted least squares formula:

where W is a matrix of weights. Design-based variances for these regression coefficients can be estimated using the formulas in equations (13) to (15) where:

For logistic regression models, the assumptions are:

The estimated impacts using the regression approach should be similar to the differences-in-means impact estimates, because the covariates should be uncorrelated with treatment status due to random assignment. However, the standard errors of the impact estimates should be smaller using the regression models because the covariates are likely to be correlated with the outcome measures, and hence, are likely to reduce intraclass correlations.
iii. Estimating Impacts for Participants and Adjusting for Crossovers
The experimental framework will provide unbiased estimates of the impact of the opportunity to receive specific WIA services (intent-to-treat [ITT] effects). However, since some sample members may decide not to use the offered WIA services, the net impacts on just those who participate in the program (treatment-on-the-treated [TOT] effects) are also of interest.
Crossovers occur if customers assigned to one research group receive WIA services for which they are ineligible given their study assignment to the core or core-and-intensive group. Our main approach to crossovers is to prevent them. Site staff will be carefully trained on the importance of not undermining the experiment. We will monitor the extent of crossovers by collecting administrative data on service receipt from the sites. In the National Job Corps Study, only 1.2 percent of control group members enrolled in Job Corps before their restriction period ended (Schochet et al. 2001). If we find that more than five percent of customers cross over, we will adjust using techniques similar to the one we describe below for addressing whether study participants do not receive services.
Methods to adjust for nonparticipation and research group crossovers are complex because research groups will be offered different combinations of services. Thus, both the full-WIA and the core-and-intensive services research groups under investigation could have nonparticipants and crossovers. This problem becomes more tractable under certain assumptions, in which case policy-relevant TOT estimates can be generated, although they must be interpreted carefully. Assuming that crossovers are few enough that they will not require an adjustment, TOT impacts will be estimated using two potential approaches.
First, assuming the treatment has no impact on those who did not receive the service, the Bloom adjustment will be used to calculate the impact of the treatment on those who did receive the service. The TOT impact is calculated by dividing the estimated ITT impact from the full sample by the proportion of the relevant group that received services (Angrist et al. 1996; Bloom 1984). In our case, a participant will be defined as a customer who receives any intensive services or training. Bloom adjustment procedures will be applied to the various contrasts:
Impacts of the receipt of intensive services. These impacts can be obtained by dividing the difference between the mean outcomes of those in the core-and-intensive services and core groups by the percentage of core-and-intensive services group members who received intensive services.
Impacts of the receipt of training beyond core and intensive services. These impacts can be obtained by dividing the difference between the mean outcomes of the full-WIA and core-and-intensive services groups by the difference between the participation rates for the two groups. These TOT estimates must be interpreted carefully because they will reflect both the receipt of training services as well as differences in the amount of intensive services received by the two groups.
The second approach for obtaining TOT estimates uses counselors’ predictions on how likely each customer would be to receive intensive services and training, if offered. The study registration form (SRF) requests that the WIA counselor, using check boxes, indicate the likelihood that each customer eligible for random assignment will receive WIA training services. This information will be obtained prior to random assignment, and thus, will be available for all members of the FW, CI, and C research groups. The accuracy of these predictions will be assessed by comparing predicted and actual training receipt designations for members of the FW group.
If these predictions are highly accurate, we will estimate TOT impacts on the actual receipt of WIA intensive services and training by comparing the mean outcomes of predicted trainees in the FW and C groups. To assess TOT impacts of the actual receipt of training, beyond intensive services, we will compare the mean outcomes of predicted trainees in the FW and CI groups and divide this impact by the proportion of the CI group that receives intensive services (to account for some customers in the CI group who do not receive intensive services).
We will also use additional baseline data from the study registration forms along with propensity scoring methods to obtain more precise training predictions and impacts (Schochet and Burghardt 2007). This will be done in three stages, which we discuss using the FW and C groups. In the first stage, we will use the FW group only to estimate a logit model that regresses an indicator variable that equals 1 for those who actually received training and 0 for those who did not on indicators of the counselor training predictions and other baseline covariates. In the second stage, we will compute predicted probabilities (propensity scores) for both FW and C members using the parameter estimates from the model. Because of random assignment, the parameter estimates pertain not only to the FW group but also to the C group.
There are two options for the third stage. One option—the traditional method—is to use the estimated propensity scores to match a C member to each FW member (with replacement) using nearest neighbor, caliper, or kernel matching. Trainee impacts would then be obtained by comparing the outcomes of actual trainees in the FW group to their matched C members. The second option—the cutoff method—obtains a “predicted” trainee group by selecting FW and C members with propensity scores larger than a cutoff value. Trainee impacts would then be estimated by comparing FW and C members in the predicted trainee group. Under this approach, it is natural to select the cutoff value so that the proportion of all FW members in the predicted trainee group is the same as the proportion of all FW members who actually received training (see Schochet and Burghardt, 2007 for more details).
iv. Estimating Impacts for Subgroups
Subgroup analyses will address the question of whether access to a certain tier of WIA services or training is more effective for some subgroups than others. Analyses will be conducted for subgroups defined by customer characteristics and for subgroups defined by program and community characteristics. The first set of subgroup analyses will determine the extent to which specific services benefit customers with different baseline characteristics, such as age, sex, race/ethnicity, education level, and employment history. The second set of subgroup analyses will determine the extent to which key LWIA characteristics, such as performance on DOL’s common measures, quality of implementation, site size, and local area characteristics, are related to observed impacts.
Impacts
for each subgroup will be estimated in turn using a straightforward
modification to equation (9), where, for simplicity of exposition, an
analysis contrasting two research groups is assumed and the subgroup
indicator
 is
defined at the individual level and has two levels (for example,
is
defined at the individual level and has two levels (for example,
 for
females and
for
females and
 for
males):
for
males):
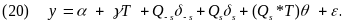
Equation
(20) differs from equation (9) because of the inclusion of the
interaction term,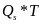 ,
and where
,
and where
 represents the vector of baseline covariates that excludes
represents the vector of baseline covariates that excludes
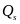 . The
regression-adjusted impact for those with
. The
regression-adjusted impact for those with
 (for
example, females) is
(for
example, females) is
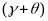 , and
for those with
, and
for those with
 (for
example, males), it is
(for
example, males), it is
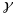 . The
parameter
. The
parameter
 represents the difference in the impacts across the two
subgroup levels. Equation (20) can be generalized to subgroups with
more than two levels (such as race/ethnicity) by including additional
treatment-by-subgroup indicator variables and using F-tests to
assess whether differences in impacts across subgroup levels are
statistically significant.
represents the difference in the impacts across the two
subgroup levels. Equation (20) can be generalized to subgroups with
more than two levels (such as race/ethnicity) by including additional
treatment-by-subgroup indicator variables and using F-tests to
assess whether differences in impacts across subgroup levels are
statistically significant.
v. Construction of Weights and Nonresponse Adjustments
All impact analyses will be conducted using sample weights that adjust for the sample design and for site and customer nonresponse, so that the design-based impact estimates can be generalized to the customer universe for the evaluation. The primary analysis sample will include the 26 originally-selected sites that agreed to participate in the study. A secondary analysis sample for the sensitivity analysis will also include the two replacement Midwest sites. For this secondary analysis using the 28-site sample, we will construct weights assuming that the two replacement sites were “original” sites.
For both the primary 26-site sample and the secondary 28-site sample, the survey weights will be obtained by first calculating the following selection probability for each survey respondent:
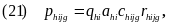
where
 is
the probability that customer j in region h, site i,
and research group g completes a follow-up interview;
is
the probability that customer j in region h, site i,
and research group g completes a follow-up interview;
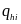 is
the probability that site i in region h is selected for
the study;
is
the probability that site i in region h is selected for
the study;
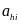 is
the probability that a selected site agrees to participate in the
evaluation;
is
the probability that a selected site agrees to participate in the
evaluation;
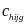 is
the probability that a customer within a participating site is
selected for follow-up interviews; and
is
the probability that a customer within a participating site is
selected for follow-up interviews; and
 is
the probability that the customer is a survey respondent. The weight
for a customer,
is
the probability that the customer is a survey respondent. The weight
for a customer,
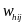 , will
then be computed to be inversely proportional to
, will
then be computed to be inversely proportional to
 .
.
Calculating
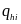 and
and
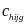 .
The probability that a site is selected for the study (
.
The probability that a site is selected for the study (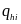 )
will be computed using the sampling probabilities discussed above
that are based on recent WIASRD data on the number of LWIA customers
who received intensive services. Similarly, values for
)
will be computed using the sampling probabilities discussed above
that are based on recent WIASRD data on the number of LWIA customers
who received intensive services. Similarly, values for
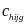 will
be obtained using the customer sampling probabilities to the various
research groups from above.
will
be obtained using the customer sampling probabilities to the various
research groups from above.
Calculating
 .
As discussed, 30 sites were randomly selected for the study, 26
agreed to participate, and two Midwest sites were selected as
replacements for two refuser Midwest sites. Sites who refused to
participate may differ from more cooperative sites in ways that are
potentially related to customer outcomes and impacts. If not
corrected, the effects of site nonresponse could lead to biased
impact estimates.
.
As discussed, 30 sites were randomly selected for the study, 26
agreed to participate, and two Midwest sites were selected as
replacements for two refuser Midwest sites. Sites who refused to
participate may differ from more cooperative sites in ways that are
potentially related to customer outcomes and impacts. If not
corrected, the effects of site nonresponse could lead to biased
impact estimates.
To examine the effects of site nonresponse, the contractor will first conduct statistical tests (chi-squared and t-tests) to gauge whether the characteristics of responding sites are fully representative of the 30 sites. These analyses will be conducted using the following data: strata indicators used for site selection (region, size, and training rate), WIA funding levels, additional customer characteristics in the WIASRD data, and local area data (such as the unemployment rate) in the ARF data.
Our
primary approach for adjusting for site nonresponse will be to
calculate
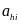 using
the following propensity score matching procedure:
using
the following propensity score matching procedure:
Estimate a logit model predicting site nonresponse. A binary variable—equal to 1 for a participating site and zero for a nonparticipating site—will be regressed on the variables listed above.
Calculate a propensity score for each site. This score is the predicted probability that a site is a respondent, and will be constructed using the parameter estimates from the logit regression model and the site’s covariate values. Sites with large propensity scores are more likely to be respondents, whereas sites with small propensity scores are more likely to be nonrespondents.
Construct response probabilities (the
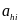 probabilities) using the estimated propensity scores. The
response probability for a site will be calculated as the site’s
estimated propensity score. It is important to note that the
propensity score procedure adjusts only for observable
differences between site respondents and nonrespondents. The
procedure does not adjust for potential unobservable differences
between the two groups. Thus, this procedure only partially adjusts
for potential nonresponse bias.
probabilities) using the estimated propensity scores. The
response probability for a site will be calculated as the site’s
estimated propensity score. It is important to note that the
propensity score procedure adjusts only for observable
differences between site respondents and nonrespondents. The
procedure does not adjust for potential unobservable differences
between the two groups. Thus, this procedure only partially adjusts
for potential nonresponse bias.
Calculating
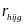 .
Survey nonresponse can also bias impact estimates if outcomes of
survey respondents and nonrespondents differ. To assess whether
survey nonreponse may be a problem for each follow-up survey, three
general methods will be used:
.
Survey nonresponse can also bias impact estimates if outcomes of
survey respondents and nonrespondents differ. To assess whether
survey nonreponse may be a problem for each follow-up survey, three
general methods will be used:
Comparing the baseline characteristics of survey respondents and nonrespondents within research groups. We will conduct statistical tests to gauge whether those in a particular research group who respond to the interviews are fully representative of all those in that research group. The statistical tests will use baseline data from the SRF (which will be available for the full research sample). For each baseline characteristic, we will test whether there are significant differences between customers who responded to the follow-up survey and those who did not respond to the follow-up survey, using t-tests to test for significant differences in univariate characteristics (such as age) and chi-square tests to test for significant differences in categorical variables (such as educational attainment). These tests will be conducted separately for each research group. Noticeable differences between respondents and nonrespondents could indicate potential nonresponse bias and limit the generalizability of the study results if not taken into account.
Comparing the baseline characteristics of respondents across research groups. Tests for whether the baseline characteristics of respondents across research groups differ from each other will be conducted. Similar to the comparisons between respondents and nonrespondents, for each baseline characteristic on the SRF, we will test whether there are significant differences in baseline characteristics for respondents in each of the three research groups, again using t-tests for univariate characteristics and chi-square tests for categorical variables. Statistically significant differences between respondents in different research groups could indicate potential nonresponse bias and limit the internal validity of the study if not taken into account.
Comparing impacts for respondents and nonrespondents using administrative data. Administrative outcome data will be available for both survey respondents and nonrespondents. To gauge the extent to which survey nonresponse may be a problem, statistical tests will be conducted to assess whether estimated impacts based on administrative outcome data differ for survey respondents and those in the survey sample who did not respond to the survey. This will be done in the same framework as the subgroup analysis described in Equation (3) and the accompanying text, where the subgroup is follow-up survey response status. The parameter estimate for λ represents the estimated difference in the impacts for survey respondents and nonrespondents.
Two
approaches for correcting for potential survey nonresponse bias will
be used in the estimation of program impacts based on survey data.
First, adjustments for any observed differences between respondents
across the various research groups will be performed by including
baseline characteristics of the respondents in all the regression
models. Second, because this regression procedure will not correct
for differences between respondents and nonrespondents, we will
construct values for
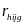 so
that the weighted observable baseline characteristics are similar for
respondents and the full sample that includes both respondents and
nonrespondents. For each survey instrument and research group, the
study will construct
so
that the weighted observable baseline characteristics are similar for
respondents and the full sample that includes both respondents and
nonrespondents. For each survey instrument and research group, the
study will construct
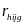 using
the propensity score methods discussed above, where (1) a logit model
will be estimated that predicts interview response using baseline
data, and (2)
using
the propensity score methods discussed above, where (1) a logit model
will be estimated that predicts interview response using baseline
data, and (2)
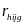 will
be calculated as the predicted propensity score.
will
be calculated as the predicted propensity score.
This propensity score procedure will yield large weights for those survey respondents with characteristics associated with low response rates (that is, for those with small propensity scores). Similarly, the procedure will yield small weights for those respondents with characteristics that are associated with high response rates. Thus, the weighted characteristics of respondents should be similar, on average, to the characteristics of the entire research sample.
Poststratification. The study will not poststratify the sample for several reasons. First, the study initially selected the sample using stratified random sampling methods, and thus, will obtain proportionate representation within key subgroups of the WIA customer population. Second, because of large sample sizes, stratified random selection will tend to generate proportionate sample sizes even across customer subgroups that are not used to define the initial strata. Finally, the study will not obtain additional key data items on individual sample members and the full sample universe after sampling that will be useful for adjusting the means of the treatment and comparison groups using poststratification methods. Thus, the sample weights for the study will not be adjusted for poststratification.
Multiple Imputations. To test the sensitivity of our results to this propensity score procedure, we will also use multiple imputation procedures (Rubin 1976) that replace missing customer outcomes with a set of plausible values that represent the uncertainty about the correct imputed value. We will generate five multiply imputed data sets, analyze them using standard procedures for complete data, and combine the results from these analyses. This multiple imputation technique has become quite commonly used in experimental evaluations of social policy interventions (Puma et al. 2009; Rubin 1987).
Specifically, we will use the regression method where a regression model is fitted for each variable with missing values, with the previous variables as covariates. The models will include both site-level and customer-level baseline variables. Based on the fitted regression coefficients, a new regression model will be simulated from the posterior predictive distribution of the parameters and will be used to impute the missing values for each variable. This process will be repeated sequentially.
We
will estimate impacts using each of the five data sets and using the
sampling weights. Let
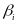 be
the estimated impact for data set i. The final estimate for
the treatment effect will be the mean of the
be
the estimated impact for data set i. The final estimate for
the treatment effect will be the mean of the
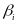 (that
is,
(that
is,
 ).
).
The
standard error of the combined estimate will be calculated from (1) a
within-imputation variance component, (2) a between-imputation
variance component, and (3) an adjustment factor for the number of
repetitions (D=5 in our case). Let Wi be
the estimated variance of the parameter from repetition i. Then the
within-imputation variance is
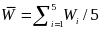 , the
between-imputation variance component is
, the
between-imputation variance component is
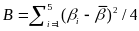 , and
the total variance is
, and
the total variance is
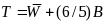 ,
which will be used for significance testing.
,
which will be used for significance testing.
b. Degree of Accuracy for the Impact Estimation
A sample size that is adequate to detect any net impacts that are large enough to be policy relevant is key to the success of the evaluation. This section presents minimum detectable impacts (MDIs) on quarterly earnings—one of the key outcomes of the evaluation—for both the survey and administrative record samples for the sample of 26 sites (Table B.6). In calculating the MDIs, a five percent significance level and two-tailed test are assumed. The power calculations incorporate design effects stemming from the clustering of individuals within sites and the use of sampling weights, as well as multiple comparison adjustments.
Variances under a clustered design. To consider sources of variance under a clustered design, a hypothetical unclustered simple random assignment design in which customers would be randomly assigned to each research condition across all LWIAs is considered first. Under this design, the variance of the estimated impact on an outcome measure (that is, the difference between the mean outcomes of those assigned to two research groups being compared) must account for between-customer variance only and can be expressed as follows:
![]()
where
k1 is the number of customers in the first
research group, k2 is the number of
customers in the second research group, and
![]() is the variance of the outcome measure.
is the variance of the outcome measure.
Under the two-stage design proposed for the evaluation, study sites will first be randomly selected from the universe of LWIAs, and then study-eligible WIA customers within the study sites will be randomly assigned to the research groups. Under this design, there is clustering at the site level. Intuitively, if sampling were repeated, a different set of sites would be selected, which introduces additional variance to the impact estimates relative to the simple random sample design discussed above. Mathematically, the variance expression becomes
![]()
where s is the number of study sites (s = 30), is the between-site variance as a proportion of the total variance of the outcome measure—the intraclass correlation—and f is the finite population correction at the site level. If there is no between-site variance (that is, if mean customer outcomes are the same in every LWIA), then = 0 and equation (5) reduces to equation (4). Even if is small, design effects from clustering can be large because the site-level term in the variance expression is deflated by the number of sites, not the much larger number of customers. However, if the sites in the selected sample represent a large proportion of the total WIA customer population, then the finite population correction reduces the site-level term in proportion to the share of the population represented by the sample. For example, if half of the customers are represented by the sampled sites—that is, f = 0.50—then the site-level variance term is half of what it would have been otherwise.2 If all of the sites were selected—that is, f = 1—then the site-level term would disappear. The within-site correlation between the outcomes of those assigned to the two research groups is captured by the parameter c and is likely to be positive. Thus, this correlation will likely reduce the variance and, hence, the design effects, due to clustering.
An equivalent way of expressing equation (5) is as follows:
![]()
where
![]() is
the variance of the net impacts across sites. Thus,
design effects will be small if impacts are similar across LWIAs,
which would occur if c is close to 1 or
is close to 0 in equation (5). Based on data from recent
employment-related impact evaluations on populations similar to the
WIA population, the value of c is set to 0.7 and
is equal to 0.04 in the MDI calculations. Estimates of rho and c
come from three sources: (1) DOL’s National Evaluation of the
Trade Adjustment Assistance Program that included a national sample
of workers filing for UI benefits across 26 randomly selected
states and hundreds of local workforce areas, (2) DOL’s
Evaluation of the Individual Training Account Demonstration; and (3)
DOL’s National Job Corps Evaluation which contained national
samples across 100 Job Corps centers nationwide. In the simulations
used to test the sampling procedure, as discussed in Subsection 1a
above, design effects from clustering and weighting were calculated
in each of the simulated random draws. On average, design effects
that incorporate both clustering and weighting effects are expected
to be about 1.51 for impacts based on the follow-up interview
sample—that is, the variance is about 51 percent larger
compared to an unclustered, self-weighting design—and this
estimated design effect did not vary much across the simulations.
For the administrative records sample, the site-level term is a
larger proportion of the total variance, and as such, the design
effect for the administrative records sample is larger, 2.25, mostly
due to a greater relative effect of clustering on the variance.
is
the variance of the net impacts across sites. Thus,
design effects will be small if impacts are similar across LWIAs,
which would occur if c is close to 1 or
is close to 0 in equation (5). Based on data from recent
employment-related impact evaluations on populations similar to the
WIA population, the value of c is set to 0.7 and
is equal to 0.04 in the MDI calculations. Estimates of rho and c
come from three sources: (1) DOL’s National Evaluation of the
Trade Adjustment Assistance Program that included a national sample
of workers filing for UI benefits across 26 randomly selected
states and hundreds of local workforce areas, (2) DOL’s
Evaluation of the Individual Training Account Demonstration; and (3)
DOL’s National Job Corps Evaluation which contained national
samples across 100 Job Corps centers nationwide. In the simulations
used to test the sampling procedure, as discussed in Subsection 1a
above, design effects from clustering and weighting were calculated
in each of the simulated random draws. On average, design effects
that incorporate both clustering and weighting effects are expected
to be about 1.51 for impacts based on the follow-up interview
sample—that is, the variance is about 51 percent larger
compared to an unclustered, self-weighting design—and this
estimated design effect did not vary much across the simulations.
For the administrative records sample, the site-level term is a
larger proportion of the total variance, and as such, the design
effect for the administrative records sample is larger, 2.25, mostly
due to a greater relative effect of clustering on the variance.
Multiple comparisons problems and solutions. The evaluation will randomly assign adult and dislocated workers to three research groups. Thus, there are three possible contrasts for analysis:
1. Comparisons of the full-WIA group to the core-and-intensive group
2. Comparisons of the full-WIA group to the core group
3. Comparisons of the core-and-intensive group to the core group
Suppose separate t-tests were conducted for each contrast to test the null hypothesis of no impacts, where the type I error rate (statistical significance level) is set at = five percent for each test. This means that the chance of erroneously finding a statistically significant impact is five percent. However, when the hypothesis tests are considered together, the “combined” type I error rate could be considerably larger than five percent. For example, if all null hypotheses are true, the chance of finding at least one spurious impact across the three tests would be 14 percent (assuming that the tests are independent). Thus, without accounting for the multiple comparisons being conducted, there is a greater chance that the study will erroneously conclude that some particular treatment is preferred over others. A similar issue arises when considering estimating program impacts on many outcome measures or for many different subgroups of customers—the probability of finding spurious impacts increases greatly.
At the same time, statistical procedures that correct for multiple testing typically result in hypothesis tests with reduced statistical power—the probability of rejecting the null hypothesis given that it is false. Stated differently, these adjustment methods reduce the likelihood of identifying real differences between the contrasted groups because controlling for multiple testing involves lowering the type I error rate for individual tests, with a resulting decrease in the power to detect statistically significant impacts when the program is indeed effective (Schochet 2008b).
The MDI calculations for the full sample adjust for multiple comparison testing. One MDI adjustment approach, based on the Bonferroni method, is to calculate MDIs in which the usual significance level ( = five percent) is divided by the number of tests (three in the case of the main contrasts). This approach is conservative because it assumes independent tests, even though the tests are correlated because of the repetition of each research group sample across tests. Instead, the less conservative Tukey-Kramer method that accounts for the repetition of research groups in each comparison will be used (Kramer 1956; Tukey 1953).
The multiple comparisons problem also occurs when tests of intervention effects are conducted across multiple outcomes. To address this issue, outcomes for which the analysis is confirmatory versus outcomes for which the analysis is exploratory will be distinguished. The confirmatory analysis will focus on priority outcomes—average quarterly earnings and employment—and provide estimates whose statistical properties can be stated precisely. The goal of this analysis will be to present rigorous tests of the study’s central hypotheses; for these analyses, significance levels will be adjusted for multiple testing. Confirmatory analyses will be limited to estimates based on the full sample of customers.
The purpose of exploratory analysis, on the other hand, will be to examine other outcomes of interest, such as participation in training and receipt of public assistance, for which impacts might exist. The aim of this analysis will be to identify hypotheses that could be subject to more rigorous future examination. For the exploratory analysis, multiple comparison adjustments will not be made.
Finally, the multiple comparisons problem also arises when considering many subgroups for which separate impacts are estimated. Therefore, all subgroup analyses will be treated as exploratory. We will conduct F-tests of the differences in impacts within categories of subgroups. For example, we will conduct an F-test of whether the impact on older customers is different than the impact on younger customers. We will note in our report that with an alpha threshold high enough to account for the multiple comparisons among all the subgroups (not just those in a category), it is likely that no impact on a subgroup would be found significant.
Minimum detectable impacts. For the overall participant sample, we can expect to detect a significant quarterly earnings impact for each comparison if the true program impact were $161 or more using the survey sample and $127 or more using the administrative records sample (Table B.7). The MDIs are lower for the administrative records sample as we will collect administrative data on everyone in the full-WIA group and not just the 2,000 selected for the survey sample.
Table B.7. Minimum Detectable Impacts on Quarterly Earnings, for Adults and Dislocated Workers in 26 Sites that Agreed to Participate
|
Full-WIA vs. Core |
|
Full-WIA vs. Core-and-Intensive |
|
Core-and-Intensive vs. Core |
|
Quarterly
Earnings |
|
Quarterly
Earnings |
|
Quarterly
Earnings |
Survey Data |
|
|
|
|
|
Adult and dislocated workers |
161 |
|
161 |
|
161 |
WIA training participants |
316 |
|
316 |
|
NA |
Adults only |
169 |
|
169 |
|
169 |
Dislocated workers only |
198 |
|
198 |
|
198 |
50% subgroup of customers |
181 |
|
181 |
|
181 |
50% subgroup of sites |
200 |
|
200 |
|
200 |
Administrative Data |
|
|
|
|
|
Adult and dislocated workers |
127 |
|
127 |
|
151 |
WIA training participants |
249 |
|
249 |
|
NA |
Adults only |
127 |
|
127 |
|
127 |
Dislocated workers only |
144 |
|
144 |
|
157 |
50% subgroup of customers |
134 |
|
134 |
|
168 |
50% subgroup of sites |
159 |
|
159 |
|
188 |
Notes: The MDI formula used for the calculations is as follows:
![]()
where is the standard deviation of quarterly earnings ($1,250) based on results from previous similar studies, f is the finite population correction (0.247), r is the response rate (0.82 for the survey, 1.00 for administrative records), R2 is 0.20 both within and across sites, the intraclass correlation is 0.04, the correlation of treatment and control groups within sites c is 0.70, k1 and k2 are pertinent sample sizes for groups 1 and 2, and s is the total number of sites (26). The MDI calculations assume two-tailed tests, 80 percent power, and a five percent significance level that is adjusted for multiple testing using the Tukey-Kramer approach, yielding a factor of 3.19. For subgroup estimates, no multiple testing adjustment is made, yielding a factor of 2.80. To calculate the MDI on those who participate in training, the MDI for the full sample is divided by the estimated training rate of 51 percent.
NA = not applicable.
MDIs can also be calculated for customers who participate in training, which is an important, and often expensive, component of WIA services. About 51 percent of WIA customers who receive intensive services also participate in training. Using the Bloom adjustment, it is estimated that the MDI for full-WIA group members who participate in training—the estimate of TOT—is $316 for the survey sample and $249 using administrative records data when compared to the core-and-intensive services group. (Since only the full-WIA group is eligible for WIA-funded training, the estimated MDIs for training participants for the core-and-intensive versus core comparison are not calculated.)
MDIs as measured by the survey data are about $181 for a subgroup including 50 percent of customers. The design will also be slightly less effective at detecting impacts for subgroups of sites than for subgroups defined by customer characteristics, because of larger clustering effects, but it can still reliably detect impacts on quarterly earnings that are $200 or larger for the survey sample and $159 for the administrative sample.
The MDIs are comparable to the inflation-adjusted quarterly earnings impacts found for adults in the National JTPA Study (Bloom et al. 1993). The MDIs also suggest that the study will have sufficient precision to assess whether the impact of the WIA services are sufficient to justify the costs. The ITA Experiment found that the cost of WIA-funded training on average was about $3,200 per customer (McConnell et al. 2006). Hence, for the benefits from increased earnings to outweigh the costs of training, earnings would need to increase by more than $320 per quarter on average over the 30-month period. The MDIs are sufficiently small that we will be able to detect an impact as small as $320 per quarter for the full sample with either the survey or administrative data.
c. Analysis Methods and Degree of Accuracy for the Benefit-Cost Analysis
The question of the effectiveness of WIA Adult and Dislocated Worker programs extends beyond whether the services they provide are effective at improving training or employment outcomes, to whether the benefits these services accrue are large enough to justify their costs. A benefit-cost analysis uses an accounting framework to itemize the relative benefits and costs of the three service tiers. Benefits include increased earnings and taxes paid after receiving the services. Costs include foregone earnings while receiving the services and the resources used to provide the services. We will use information from participant surveys and the cost data collection package to assign a dollar value to each measured program impact and cost.
WIA
Adult and Dislocated Worker programs affect multiple stakeholders.
For example, any increase in earnings as a result of participating in
job training financed by an ITA is a benefit
to customers. Yet
the value of the ITA used to pay for that training is a cost to the
government. We will examine the benefits and costs from the
perspectives of the customers, the government/taxpayers, and society
as a whole. The benefits and costs to society are the sum of those
for customers and the government, and are therefore calculated
irrespective of who actually reaps the benefits or pays the costs.
Thus, any benefit to either customers or the government is a benefit
to society and, likewise, any cost to either customers or the
government is a cost to society. Using the accounting framework,
some benefits and costs cancel each other out from the perspective of
society because they are a benefit to one group but an equal cost to
another. For example, an increase in taxes is a benefit to the
government and taxpayers, but a cost to customers who pay them, and
are neither a cost nor a benefit to society.
The first step in the benefit-cost analysis is to measure four potential benefits of WIA Adult and Dislocated Worker programs: (1) earnings and fringe benefits, which are benefits to customers and society; (2) taxes associated with higher earnings, which are a benefit to the government, a cost to customers, but cancel each other out from society’s perspective; (3) UI benefits and administrative costs, which are a benefit to customers, a cost to government, and a net cost to society (since administrative costs are not recouped by customers receiving UI benefits); and (4) public assistance receipt, which is a transfer from government to customers but, like UI, has associated administrative costs that result in a net cost to society. The estimates of the benefits from increased earnings, UI, and public assistance receipt will be derived directly from estimated impacts. The estimated benefits from increased fringe benefits, taxes, and UI and other public assistance programs will be derived from publicly available statistics.
The second step is to assign costs associated with providing WIA Adult and Dislocated Worker services to each sample member. The cost components associated with each service are described below (and listed in column 1 of Table A.3 in Part A):
Resource room. The resource room is predominantly self-serve; although a program employee typically staffs the resource room to provide assistance logging on to computers, enforcing time limits, and directing customers to relevant materials. Therefore, the primary cost components of the resource room are overhead (for example, rent, utilities, and internet service provider fees) and employee time to staff the room, including both salary and fringe benefits. Since many people use the resource room at the same time, we must also have a measure of how many people visit the resource room in order to calculate the average cost of a visit to the resource room.
Workshops. The primary cost component of a workshop is staff time to prepare for, conduct, and follow up after the workshop. In addition, there might be costs of workshop-specific workbooks or other materials. Since more than one person typically attends a workshop, to calculate a per-participant cost of attending a workshop we must also know the number of attendees who typically attend.
Peer support groups. A staff person typically moderates the peer support group; this would be the primary cost of such a meeting. Since more than one person typically attends a peer support group, to calculate a per-participant cost of attending a peer support group we must also know the number of attendees who typically attend.
Assessments. The main cost components of assessments are the materials associated with paper-and-pencil assessments (for example, test booklets), licensing fees associated with online assessments, and any scoring fees associated with either type of assessment. The time counselors spend on discussing the findings from assessments with customers is accounted for in the individualized meetings with counselors.
Individualized counseling. The primary cost component of a meeting with a counselor is the cost of that counselor’s time spent preparing for, conducting, and following up on the one-on-one meetings (including salary and fringe benefits).
Supportive services. The cost of supportive services is simply the dollar value of those services, plus the cost of any counselor time to determine need for and process supportive services payments.
The cost of education or training is the cost to enroll in the program; the costs to attend these types of programs can be paid by an ITA, but can also be paid with other forms of financial aid or out-of-pocket.
In addition to the services customers can receive directly, American Job Center managers, supervisors, and staff such as receptionists and administrative assistants, closely support the work of the front line staff. Therefore, their salaries and fringe benefits contribute to the cost of delivering each service. Similarly, overhead costs are necessary for operating the programs, but are not associated with a particular activity. These include rent and utilities, computers, internet access, furniture, office supplies, and phone and fax lines. To incorporate these administrative and overhead costs, we will calculate these costs per counselor hour and add them to the labor costs.
Costs will be assigned using information from data on what services or training participants received, as reported on the surveys, combined with the information on the cost per service and training collected from the cost data collection package, administrative data, and the surveys.
To illustrate the methodology of estimating costs, consider a core-and-intensive service group member who indicates having spent five hours meeting one-on-one with a counselor. Using the cost collection forms, we will collect information on staff salaries and the cost of fringe benefits as a percentage of salaries and then calculate the total hourly cost of staff time. For example, if a counselor earns $35,000 per year, the work year includes 2,080 hours, and fringe benefits equal 25 percent of salaries, we estimate an hourly cost of staff time at $21.03 ($35,000 ÷ 2,080 x 1.25). This hourly rate will be combined with information collected from activity logs on the amount of preparation and follow-up time corresponding to each hour of one-on-one meetings to assign a total cost to each activity involving staff time. For instance, if counselors typically spend 30 minutes in preparation and follow-up work for each hour with a customer, then we would value that hour of face-to-face time with the counselor at $31.55 ($21.03 x 1.5).
We must then apply an administrative and overhead cost to the hour of one-on-one meeting time. To do so, we will divide total annual program administration costs (for example, administrative staff salaries and fringe) by the number of front-line staff and hours worked per year to get an hourly administration rate per full-time equivalent front-line staff person. We will do the same with overhead costs and apply both rates to the hourly staff costs associated with delivery of each service to get a loaded labor rate. For example, if total program administration and overhead costs per year are $250,000, there are 50 full-time equivalent front-line staff, and a full time equivalent year consists of 2,080 hours, we estimate an hourly cost of program administration per front-line staff at $2.40 ($250,000 ÷ 50 ÷ 2,080). This increment will be added to the salary plus fringe hourly rate of front-line staff to result in a loaded hourly labor rate of $33.95 ($31.55 + $2.40). Thus, the total cost of the five face-to-face meetings with a counselor would be $169.75.
A similar approach will be used to compute the staffing costs associated with other services such as workshops and assessments. When applicable, costs of materials or scoring fees will also be incorporated. Summing the costs of each of the services a customer received together, we will arrive at a total cost per participant.
We will then compare the costs per participant—which are borne predominantly by the government and society—with the benefits per participant, as viewed from the perspective of the customer, government, and society, as described previously. The following example illustrates the three perspectives of interest in the benefit-cost analysis. Suppose a customer received $300 of services and paid nothing for them out-of-pocket, so the government bore all the costs. Suppose this customer experienced an increase in earnings of $1,000 per year—which is taxed at 15 percent—but had no change in UI or other public assistance receipt. Then the cost to the customer is zero dollars and the benefit is $850 ($1,000 minus $150 in taxes), so the net benefit from the customer’s perspective is $850. The government paid out $300 and is receiving $150 in increased taxes, so the net benefit from its perspective is minus $150. From society’s point of view, the net benefit is the sum of the net benefits to the customer and the government, so the net benefit is $700.
The final step in the benefit-cost analysis is to sum the net benefits across participants in each of the study groups. By comparing these differences in benefits and costs across the three study groups, we can determine each group’s relative cost effectiveness.
d. The VSS Analysis Methods
The study will document services as they are currently implemented, the experiences of veterans and nonveterans as they move through the system, the activities and interactions of various types of staff, outcomes for veterans, and any special needs of veterans or issues around serving them. The main sources of data for the implementation analysis are site visits that will be conducted to each of the 28 sites. In each site, the VSS team will conduct interviews in the LWIA’s American Job Centers selected for the WIA Evaluation’s second round of implementation study visits. The sample will include centers of different sizes and in different areas (although they may be geographically clustered so that the evaluation team can visit the centers in the time available). While specific on-site activities may vary somewhat from center to center, across the LWIAs, the VSS will interview up to six American Job Center staff members and an average of two LVER and DVOP staff. Each LWIA’s state veteran coordinator will also be interviewed. At eight of the sites, focus group interviews will be conducted with veteran customers, and reviews of individual case files will be undertaken.
An important part of the implementation study will be ensuring the accuracy and reliability of both the data and the conclusions derived through analysis of the data. As described in more detail in Section B.3, strategies to ensure that the data are reliable and as nearly complete as possible include flexibility in scheduling of visits and the assurance given to respondents of the privacy of the information that they provide. Furthermore, training of site visitors on how to consistently use the protocols will facilitate a high degree of accuracy in the data. In addition, shortly after each site visit, the visitors will synthesize the data from each on-site activity to the requirements of a structured write-up guide. Because most questions will be asked of more than one respondent during a visit, the analysis will allow for triangulation of the data so that discrepancies among different respondents can be interpreted.
Because the WIA program differs by LWIA and operates in very different environments, and because the types and densities of veterans vary by LWIA, there is no single, precise, uniform implementation experience at LWIAs across the country. In recognition of this, the analysis will identify both themes that span across the 28 sites and distinctive features or patterns that occur in only a subset of the 28 sites.
The VSS will also analyze two sets of administrative data that states report to DOL: WIASRD and Wagner-Peyser data. These data sets describe the veterans who have registered for services and the employment-related services they received. Since these data include customers’ employment and earnings (through UI wage matching), we will not conduct special UI wage matching. The data used for the analysis will include only veterans and will be stripped of any identifying information. The analysis of the data will include an exploration of veteran characteristics, the services they receive, and the outcomes they achieve. The analyses will also seek to identify any associations between specified “service menus” and outcomes experienced by different veterans subgroups.
3. Methods to Maximize Response Rates and Data Reliability
The methods to maximize the response rates and data reliability are discussed for each data collection effort that is part of this request for clearance.
For the WIA Evaluation
a. Follow-up Surveys
The contractor will use well-established methods to maximize response rates and data reliability for the 15- and 30-month follow-up surveys. We have used the methods described below in other data collection efforts, such as the Trade Adjustment Assistance (TAA) Study (OMB number 1205-0460) and the Individual Training Account (ITA2) Follow-up Study (OMB number 1205-0441).
The strategy for maximizing response to the follow-up surveys begins with the survey development and carries through the entire survey process. The methods employed mitigate all types of individual nonresponse, from failure to locate the sample member to a refusal to participate in the survey. Using the methods for the two follow-up surveys that follow, we expect to obtain a response rate of at least 82 percent.
Survey development. Elements of the survey development and administration itself can support high response:
Survey language and length. The two follow-up questionnaires are designed to be easy to complete. The questions are written in clear and straightforward language. The average time required for the respondent to complete the survey is estimated at 40 minutes for the 15-month follow-up and 30 minutes for the 30-month follow-up.
Multilanguage survey administration. During telephone contact, interviewers will identify Spanish-speaking respondents and connect or schedule them to speak with a bilingual interviewer. Also, if the study intake documents (consent, study registration, or contact information forms) were completed in Spanish, a bilingual interviewer will automatically be assigned the case. When necessary, translators for languages other than Spanish will be used. Mathematica employs staff who speak a wide range of languages and have experience conducting interviews in a number of languages. The intake forms have been translated into a variety of languages including Spanish, Russian, Vietnamese, Creole, Korean, and Chinese Simplified (Mainland). Mathematica will use interpreters when contacting these sample members.
Methods to enhance locating efforts, promote positive contacts with sample members, and sustain outreach efforts over time and with the toughest sample members also support high survey response:
Locating sample members. An essential step in a successful survey effort is the ability to locate as much of the survey sample as possible. The locating process will begin with the use of an independent vendor that will check the full sample against current address databases prior to any initial outreach. This first step is critical given that some sample members may have moved since the time of their entry into the study. For any mail that is returned as undeliverable after the initial advance letter (described below), the evaluation team will begin a series of extensive tracking and locating procedures that have proven successful in other Mathematica studies. These procedures include using other independent address databases and searching social networking sites. When these attempts fail to locate the sample member during the survey period, the contractor will turn to checking with neighbors and family members. At the time of study intake, customers completed a contact information form to provide contact information for up to three friends or relatives who might know how to get in contact with them at some future date (OMB clearance number 1205-0482). When talking with these contacts, the specific purpose of the call will not be disclosed, but Mathematica locators will convey that the effort to reach the sample member is for an important study being sponsored by the government.
Once all centralized efforts to locate and interview a sample member have been exhausted, with no completed interview, the evaluation team will prepare locating packets to send to local interviewers. These local interviewers will be trained on the project’s goals and the questionnaire, but their main purpose is to find the sample member and have that person call into the telephone interviewing center. The field interviewer may also discover other information about the sample member, including that they have moved, have been incarcerated, entered the military, or are deceased. In some cases, the field interviewer may receive an adamant refusal from the customer to participate in the survey. All information gleaned by the field staff will be sent back to the contractor for further determination on how to proceed.
Initial contact with sample members. Establishing the authenticity of the survey effort with sample members from the start lays an important foundation in promoting a high response. To provide sample members with an initial, official introduction to the survey, including its purpose, content, and length, the evaluation team will send an advance letter on DOL letterhead (including the evaluation project logo) shortly before fielding of the survey begins (Appendix C). This letter will (1) explain the voluntary nature of participation and their privacy protection, (2) extend the incentive offer, and (3) give a toll-free number for telephone calls. The envelope will be printed with the DOL logo to capture the sample member’s attention and to communicate the legitimacy of the study. (However, Mathematica’s return address will be used to facilitate the processing of returned mail and locating procedures.)
Mathematica staff will also work with the evaluation study sites to encourage participation in the survey by sample members. Project site liaisons will remind LWIA personnel of the survey effort in anticipation of telephone calls to confirm the legitimacy of the calls. Mathematica survey experience has shown that participants often forget about their participation in a study and sometimes call their service provider, in this case the local American Job Center, for validation of the study.
Gaining and maintaining cooperation. The evaluation team will make multiple attempts to reach all sample members through a series of outreach methods by mail and telephone. Also, the team will send out a reminder postcard to sample members who remain difficult to reach one week after the initial advance letter (discussed above) is sent. The postcard will provide a toll-free number to use to call in and complete the survey at their convenience and will prominently display the incentive amount for survey completion. Based on the experience in past survey efforts, we have found that the incentive amount captures the attention of anyone who receives the postcard—if it is not the sample member directly, then the mail recipient is more likely to pass along the postcard to its intended recipient. Another postcard providing similar information is sent out to sample members after another two weeks of nonresponse. Two more reminder letters will be sent out to nonrespondents at the midpoint of the data collection and again three to four weeks prior to the end of data collection. The advance letter and reminder postcards are provided in Appendix C.
Getting a respondent on the phone is clearly an important step, but gaining their cooperation to begin and ultimately complete the survey is paramount. Mathematica’s interviewers are highly trained in establishing rapport with respondents, gaining their cooperation, and avoiding refusals. During project-specific training, interviewers focus on skill development and role-playing to secure respondents’ cooperation and avert and convert refusals. Sample members who still refuse to participate once reached will be sent a tailored refusal-conversion letter that addresses their specific concerns. Following the letter, an expert refusal-conversion interviewer will make follow-up calls to try to gain the sample members’ cooperation.
Incentives
for survey participants. Offering an incentive for completion of
the follow-up surveys is important for obtaining the desired response
rates and reducing overall survey costs without affecting data
quality. There is substantial evidence on the benefits of offering
incentives. According to Singer et al. (2000), incentives can help
to achieve high response rates by increasing the propensity of sample
members to respond. By doing so, incentive payments have been found
to contain evaluation costs by significantly reducing the number of
calls required to resolve a
case. Studies offering incentives
show decreased refusal rates and increased contact and cooperation
rates. Incentives also increase the likelihood of participation from
subgroups with a lower propensity to cooperate with the survey
request. This is an important component of ensuring the
representativeness of the survey respondents and the quality of the
data being collected. For example, Jäckle and Lynn (2007) find
that incentives increase the participation of sample members more
likely to be unemployed. There is also evidence that incentives
bolster participation among those with lower interest in the survey
topic (Schwartz et al. 2006; Jäckle and Lynn 2007; Kay 2001),
resulting in data that are more nearly complete. Furthermore, paying
incentives does not distort responses and impair the quality of the
data obtained (as reflected in item nonresponse or the distribution
of responses) from groups that would otherwise be underrepresented in
the survey (Singer et al. 2000). Part A of this clearance package
provides additional justification for the $25 incentive payment
chosen for this demonstration.
A $25 incentive will be offered to all survey respondents. It is anticipated that about 10 percent of the survey sample will be offered $15 more, for a total of $40. This $40amount will be reserved for the most difficult to reach and hardest to convince customers. In the TAA Evaluation (OMB Control No. 1205-0460), after evaluating the outcomes of an incentive experiment conducted during the baseline survey, Mathematica obtained OMB approval for the follow-up survey to offer $25 to those sample members participating in the TAA program (treatment group) and $50 to those in the comparison group, people similar to those in the treatment group, but with no connection to TAA. This experience suggests that for the WIA evaluation, those sample members with less connection to the range of WIA services (customers placed in the core group) may be more likely to refuse the survey. The increased incentive may motivate more of them to participate.
Data reliability. The two follow-up surveys are unique to the current evaluation and will draw from a sample of participants from across all the evaluation sites, ensuring consistency in the collected data. The surveys have been extensively reviewed by project staff and staff at DOL, and have been thoroughly tested in a pretest involving six individuals from nonparticipating sites.
Evaluation sample members will be interviewed by trained members of Mathematica’s survey operations staff who are experienced working on previous studies conducted for DOL as interviewers, supervisors, and monitors. Most of these staff are familiar with similar questionnaire content and sensitive to the difficulties faced by job seekers and unemployed individuals. All survey operations staff assigned to the study will participate in both general training (if not already trained) and extensive project-specific training. Interviewers will not work on the survey until they have been certified as prepared. The project-specific training will include role-playing with scenarios and other techniques to ensure that interviewers are ready to respond effectively to questions from sample members about the study and the survey in order to illicit complete and accurate responses from respondents. A list of frequently asked questions and answers (FAQs) will be developed and included in the operational procedures manual for the survey administered via computer-assisted telephone interviewing (CATI). Interviewers will also be able to access the FAQs at any time during the survey.
When each survey administration is completed, an analysis that compares response rates in the full WIA, core-and-intensive and core groups will be conducted to assess whether there are systematic differences between the groups in the likelihood of nonresponse and in the characteristics of individuals responding to the survey. This analysis will use data from the SRF, which will be available for all sample members. These data will include the same variables used to monitor the random assignment process. If it appears that the survey respondent sample is not representative of the study sample, weights to adjust for nonresponse will be developed using propensity scoring methods. (The details of these methods are discussed previously in Part B, Section 2.)
b. Cost Data Collection Package
i. Program Costs Questionnaire
Response rates. To ensure a high response rate, a group of researchers from the evaluation team will provide technical assistance to all sites. The benefit-cost technical assistance team will have an in-depth knowledge of the types of information being sought and will work with site liaisons—who at the point of cost data collection will have worked with their sites for over a year—to familiarize themselves with site operations. Program costs questionnaires will be mailed to sites upon receiving OMB clearance and respondents will have one month to gather the cost information requested on the questionnaire and to ask questions of the technical assistance team if any items are unclear or require further explanation. Site liaisons and the technical assistance team will follow up directly with any sites that have not provided data by the end of one month. We expect to obtain a 100 percent response rate, as the data on costs are crucial to the benefit-cost analysis.
Data reliability. Several strategies will be used to ensure the reliability of the program costs data. First, a dedicated set of researchers will be trained on collecting high quality cost data, including how to determine whether the cost information reported by sites is correct and complete. These researchers will assess the quality and completeness of the cost data submitted by sites and gather additional information when necessary, working in conjunction with site liaisons. Second, the use of a questionnaire that is standardized across sites (aside from minor adjustments to reflect the organizational and funding structures of each LWIA), will ensure that the data are collected in a uniform and systematic way. This standardized approach facilitates quick identification of data items that are missing or incomplete within and across sites. Finally, respondents will be assured of the privacy of the information they provide, encouraging as much transparency in cost reporting as possible.
ii. Front-Line Staff Activity Log
Response rates. Activity logs will be distributed to a randomly selected set of counselors at two randomly selected American Job Centers in each LWIA. To ensure high response rates, local management staff will be asked to distribute the activity logs to the selected staff and encourage them to complete the logs for one week; front-line staff will have one month to return the activity log. The activity logs contain a pre-specified list of codes to capture counselors’ typical activities and minimize the time needed to complete the logs; this will also support high response rates. Site liaisons, who in many cases will have already established relationships with the selected counselors as a result of previous site visits, will follow up directly with nonresponders to encourage them to complete the activity logs. We expect completed activity logs from all randomly selected staff.
Data reliability. The use of a standardized activity log will enhance data reliability by providing a set of nine pre-specified codes from which staff can choose to indicate the activity in which they are engaged. The activity log also contains a brief set of instructions and an example to illustrate correct use of the log. In addition, the selected staff will be able to contact the benefit-cost technical assistance team if they have questions about the correct use of the log.
iii. Resource Room Sign-in Sheet
Response rates. Sign-in sheets will be distributed only to those American Job Centers that do not already have a mechanism for collecting the number of customers using the resource room in a week; centers will have one month to complete and return the sign-in sheets (the sign-in sheets need only be filled out for one week within that month). To ensure high response rates, the cover letter to the cost data collection package and the instructions on the front page of the sign-in sheet ask that resource room staff place the sign-in sheet in a prominent location and ask that all customers note their initials on the form. In addition, if a customer does not fill out the sign-in sheet, the staff person can simply enter “Customer” to reflect that a customer entered the resource room. Finally, LWIA central office staff, site liaisons, and the benefit-cost technical assistance team will follow up directly with any sites that have not provided this information.
Data reliability. LWIA central office staff and site liaisons will monitor sites using the sign-in sheets to ensure that they are placed in a prominent location and all customers are signing in. To further enhance data reliability, the benefit-cost technical assistance team and site liaisons will review submitted sign-in sheets and cross-check them with existing data about customer flow to see if the number of resource room users seems broadly consistent with that information.
For the VSS
Response Rates. The 28 LWIAs participating in the WIA Evaluation have already agreed to participate in the evaluation’s second round of implementation study visits that will include topics relevant to the VSS. Thus, we do not foresee issues in scheduling and conducting the site visits. While some staff identified for the supplemental study, such as the DVOP specialists, LVERs, and state veterans coordinators, are not WIA staff, we also do not foresee issues in garnering their participation, since the work of these staff are integral to the American Job Center services provided to veterans.
Site visitors will begin working with site staff well in advance of each visit to ensure that the timing of the visit is convenient. Because the visits will involve several interviews and activities each day, there will be flexibility in the scheduling of specific interviews and activities to accommodate the particular needs of respondents and American Job Center operations.
Data Reliability. Several well-proven strategies will be used to ensure the reliability of the data. First, site visitors, most of whom already have extensive experience with this data collection method, will be thoroughly trained in veteran services provided through the American Job Center system and issues in service delivery. Site visitors also will be instructed on how to probe for additional details to help interpret responses to interview questions. Second, this training and the use of the protocols will ensure that the data are collected in a standardized way across sites. Finally, all interview respondents will be assured of the privacy of their responses to questions.
4. Tests of Procedures or Methods
For the WIA Evaluation
All data collection procedures, instruments, and protocols to be used in the conduct of the WIA Evaluation will be tested to: (1) ensure that the procedures can be feasibly and efficiently carried out, (2) assess the clarity of the questions to be asked, (3) identify possible modifications to either question wording or question order that could improve the quality of the data, and (4) estimate respondent burden.
a. Follow-up surveys
The follow-up survey instruments were thoroughly tested with six individuals from nonparticipating sites. Mathematica employed an iterative pretesting approach; that is, survey staff administered three pretests and incorporated lessons learned before proceeding with the remaining pretests. For the initial pretests, Mathematica incorporated cognitive interviewing techniques in which respondents were encouraged to think through their responses out loud. Survey researchers encouraged respondents to identify any words and phrases that were confusing as the questions were asked rather than waiting for an end of interview debriefing. These techniques were applied to the survey introduction, answers provided to frequently asked questions, as well as to questionnaire items. The survey researchers used non-leading probes to minimize bias (for example, “I noticed you hesitated. Tell me what you were thinking”) when administering the interviews.
After the first three pilot tests were completed as cognitive interviews, the final three pretest interviews provided timing estimates. Project staff debriefed those respondents using a standard debriefing protocol to determine if any words or questions were difficult to understand and answer. Respondents in the pilot test of the follow-up surveys were given an incentive for their time completing the survey. Appendix I contains the memo summarizing the results of the pretests.
b. Cost Data Collection Package
i. Program Costs Questionnaire
To ensure that the program costs questionnaire effectively captures all the data on costs, we will pilot the questionnaire at one site during the first implementation site visit. The purpose of piloting the questionnaire is to ensure that respondents understand the data request and that the technical assistance team, working in conjunction with the site liaison, can identify areas where the forms are incomplete or incorrect. Adjustments to the questionnaire will be made as necessary.
ii. Front-Line Staff Activity Log
As with the program costs questionnaires, the activity log will be piloted at one site. The purpose of piloting the activity log is to determine whether additional response categories need to be added to capture other counselor activities and whether respondents find recording their activities for five days to be overly burdensome. Adjustments will be made as necessary.
iii. Resource Room Sign-In Sheet
Similarly, the resource room sign-in sheet will be piloted at one site; the study team will ask for feedback on the proposed approach to collecting this information for sites that do not already collect it, and whether another approach—such as having resource room staff simply keep a tally of customers—might work better.
For the VSS
To ensure that the site visit protocols are used effectively as field guides and that they yield comprehensive and comparable data across the 28 sites, senior research team members will conduct a pilot site visit before the round of site visits. The purposes of the pilot test are to ensure that the field protocols, which will guide field researchers as they collect data on-site, include appropriate probes that assist site visitors in delving deeply into topics of interest, and that the protocols do not omit relevant topics of inquiry. Furthermore, use of the protocols during a pilot site visit can enable the research staff leading this task to assess that the site visit agenda—including how data collection activities should generally be structured during each site visit—is practical, given the amount of data to be collected and the amount of time allotted for each data collection activity. Adjustments to the site visit guides will be made as necessary.
5. Individuals Consulted on Statistical Methods
No statistical methods will be used for the VSS. For the WIA Evaluation itself, consultations within the evaluation team on the statistical methods have been used to ensure the technical soundness of the study.
The following individuals were consulted on the statistical methods discussed in this submission to OMB:
Mathematica Policy Research
Dr. Kenneth Fortson (510) 830-3711
Dr. Annalisa Mastri (609) 275-2390
Dr. Sheena McConnell (202) 484-4518
Dr. Karen Needels (541) 753-0201
Dr. Frank Potter (239) 558-5956
Dr. Natalya Verbitsky Savitz (202) 554-7521
Dr. Allen Schirm (202) 484-4686
Dr. Peter Schochet (609) 936-2783
Social Policy Research Associates
Dr. Ronald D’Amico (510) 763-1499 (x628)
Dr. Andrew Wiegand (510) 763-1499 (x636)
The following individuals will be responsible for collecting the information:
Mathematica Policy Research
Survey director, Pat Nemeth (609) 275-2294
Deputy survey director, Julita Milliner-Waddell (609) 275-2206
VSS lead, Linda Rosenberg (609) 936-2762
Cost data collection lead, Dr. Mastri (609) 275-2390
The following individuals will be responsible for analyzing the information:
Mathematica Policy Research
Dr. Peter Schochet (609) 936-2783
Dr. Sheena McConnell (202) 484-4518
Dr. Annalisa Mastri (609) 275-2390
Ms. Linda Rosenberg (609) 936-2762
Dr. Natalya Verbitsky Savitz (202) 554-7521
Social Policy Research Associates
Dr. Ronald D’Amico (510) 763-1499 (x628)
Angrist, J., G. Imbens, and D. Rubin. “Identification of Causal Effects Using Instrumental Variables.” Journal of the American Statistical Association, vol. 91, no. 434, 1996, pp. 444-455.
Bloom, H. S. “Accounting for No-Shows in Experimental Evaluation Designs.” Evaluation Review, vol. 8, no. 2, 1984, pp. 225-246.
Bloom, H. S., L. L. Orr, G. Cave, S. H. Bell, and F. Doolittle. “The
National JTPA Study:
Title II-A Impacts on Earnings and
Employment at 18 Months.” Bethesda, MD: Abt Associates, 1993.
Dion, M, S. Avellar, H. Zaveri, and A. Hershey. Implementing Health Marriage Programs for Unmarried Couples. Report prepared for the U.S. Department of Health and Human Services. Mathematica Policy Research, 2006.
Jäckle, Annette, and Peter Lynn. “Respondent Incentives in a Multi-Mode Panel Survey: Cumulative Effects on Nonresponse and Bias.” Working paper presented to the Institute for Social and Economic Research, University of Essex, Colchester, United Kingdom, 2007.
Kay, Ward R. “The Use of Targeted Incentives to Reluctant Respondents on Response Rates and Data Quality.” Proceedings of the American Association for Public Research. Montreal, Canada: American Association for Public Opinion Research, 2001.
Kramer, C. Y. “Extension of the Multiple Range Test to Group Means with Unequal Numbers of Replications.” Biometrics, vol. 12, 1956, pp. 307-310.
McConnell, S., E. Stuart, K. Fortson, and others. “Managing Customers’ Training Choices: Findings from the Individual Training Account Experiment.” Report prepared for the U.S. Department of Labor, Employment and Training Administration, December 2006.
MDRC Board of Directors. Summary and Findings of the National Supported Work Demonstration. MDRC: New York City.
Murray, D. Design and Analysis of Group-Randomized Trials. Oxford: Oxford University Press, 1998.
Pocock, Stuart. Clinical Trials: A Practical Approach. Wiley-Blackwell, 1983.
Puma, Michael, Robert Olsen, Stephen Bell, and Cristofer Price. “What to Do When Data Are Missing in Group Randomized Controlled Trials.” U.S. Department of Education, Technical Methods Report, NCEE 20090049, 2009.
Rubin, D.B. Inference and Missing Data. Biometrika, vol. 63, 1976, pp. 58-592.
Rubin, D.B. Multiple Imputation for Nonresponse in Surveys. New York: J. Wiley & Sons, 1987.
Schochet, Peter Z., Jillian Berk, Ron D’Amico, and Nathan Wozny. “National Evaluation of the Trade Adjustment Assistance Program: Methodological Notes on the Impact Analysis.” Draft report submitted to the U.S. Department of Labor, 2011.
Schochet, Peter Z., John Burghardt, and Sheena McConnell. Does Job
Corps Work? Impact Findings from the National Job Corps Study.
American Economic Review, vol. 68, no. 5,
December 2008,
pp. 1864-1886.
Schochet, Peter Z. and John Burghardt. “Using Propensity Scoring Techniques to Estimate Program-Related Subgroup Impacts in Experimental Program Evaluations.” Evaluation Review, vol. 31 no 2, April, 2007.
Schochet, P. Z. “Guidelines for Multiple Testing in Impact Evaluations of Educational Interventions.” Princeton, NJ: Mathematica Policy Research, 2008a.
Schochet, Peter Z. Statistical Power for Random Assignment Evaluations of Education Programs. Journal of Educational and Behavioral Statistics, vol. 33, no. 1, 2008b, pp. 62-87.
Schochet, P.Z., S. McConnell, and J, Burghardt. “National Job Corps Study: Findings Using Administrative Earnings Records Data.” Report prepared for the U.S. Department of Labor, Employment and Training Administration, October 2003.
Schochet, P.Z., J. Burghardt, and S. Glazerman. “National Job Corps Study: The Impacts of Job Corps on Participants’ Employment and Related Outcomes.” Report prepared for the U.S. Department of Labor, Employment and Training Administration, June 2001.
Schwartz, Lisa K., Lisbeth Goble, and Edward M. English. “Counterbalancing Topic Interest with Cell Quotas and Incentives: Examining Leverage-Salience Theory in the Context of the Poverty in America Survey.” Proceedings of the American Association for Public Research. Montreal, Canada: American Association for Public Opinion Research, 2006.
Singer, Eleanor, John Van Hoewyk, and Mary P. Maher. “Experiments with Incentives in Telephone Surveys.” Public Opinion Quarterly, vol. 64, no. 2, summer 2000, pp. 171-188.
Tukey, J. W. “The Problem of Multiple Comparisons.” In mimeographed notes. Princeton, NJ: Princeton University, 1953.
U.S. Congress.
“Workforce Investment Act of 1998.” Pub. Law No. 105-220,
August 7, 1998. Retrieved from
http://www.doleta.gov/USWORKFORCE/WIA/wialaw.txt
on September 10, 2009.
2 The sampling strategy is designed to generalize to the full population of WIA sites at the time of the study (excluding small sites and sites not on the U.S. mainland), so the finite population correction is appropriate for the site-level term in the variance formula.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | Workforce Investment Act (WIA) Adult and Dislocated Worker Programs Gold Standard Evaluation |
| Author | Gretchen Kirby |
| File Modified | 0000-00-00 |
| File Created | 2021-01-25 |
© 2025 OMB.report | Privacy Policy