1205-0431 Supporting Statement, Part B_FINAL 3.28.16
1205-0431 Supporting Statement, Part B_FINAL 3.28.16.docx
Unemployment Insurance Data Validation
OMB: 1205-0431
1205-0431 Supporting Statement, Part B: Collection of Information Employing Statistical Methods
B-1. Description of universe and selection methods used.
The Unemployment Insurance Data Validation (UI DV) system assesses whether the aggregate counts of claimants, payments, determinations, appeals, etc. that are reported to the Department are valid by independently reconstructing the counts and comparing the reported counts with the reconstructed counts. The reconstructed counts are obtained from a file of individual transactions, in which each record contains all the variables needed to classify the transaction into the report cell or cells being validated; this is known as the extract file. Typically, state IT or programming staff build the extract file for each data validation population. These records are built according to exacting specifications from the underlying State database from which the reports were initially prepared, and tested to ensure that all data elements conform to Federal reporting instructions. The extracts are built with a month or quarter’s worth of data that fall into one of the 16 mutually exclusive Benefits population or 5 Tax populations. When the file passes the various tests, the counts from the file constitute the standard for correct reporting. The reconstructed counts from the extract file are compared to the reported counts submitted by state’s in UI required reports by the DV software, which is known as “report validation.” If the reported counts are within the specified tolerances of these “validation counts” they are considered valid. The “report validation” performed by state staff operating the DV software in the SUN system using an extract file tests both whether the State prepared its reports from the correct sources and whether its item-counting software works properly.
The report validation process depends critically on having an accurate file. The extract file is tested in two steps. In Step 1, the validator, typically one or two state staff members, examines and resolves all records rejected by the software as errors, removing uncountable transactions (e.g., duplicates) and fixing and reinserting into the extract file countable records by correcting syntax errors and other errors that caused the software to reject them. When that step is completed and the file is assumed to contain only countable records, in Step 2 the validator checks to see whether the records are built from data that conform to Federal reporting definitions. This is done by drawing samples from certain classes of transactions (Benefits: weeks claimed, payments, nonmonetary determinations, appeals filed/decided, overpayments; Tax: active employers, report filing, status determinations, accounts receivable) and checking key data elements in the sampled records against original UI program documentation using a master map that relates state data used for DV records to Federal definitions. If this review shows that more than 5% of the underlying records in the extract file are built from data that do not meet Federal definitions, the file is not an accurate standard for judging reported counts and it must be rebuilt, usually by the state programmers working in conjunction with the state validator(s), often after steps have been taken to correct the underlying data in the state’s database. Validation cannot move on to the report validation phase and fails at that point. Failure at this point implies that both reported counts and reconstructed counts will be based on an unknown proportion of individual transactions which do not conform to Federal reporting definitions; thus both sets of counts could be wrong, and so no conclusion about validity can be drawn from a comparison of counts.
UI DV relies on existing records from State1 UI databases and management information systems for the month or quarter being validated. The DV universe includes all records, claimants, appeals, payments/overpayments, or transactions that fall into a particular population as defined by the DV program. Data is independently reconstructed to form the extract files, without merging data with the state’s MIS. Typically, extract files are built with records from a month or quarter within one benefit year, unless otherwise specified in the DV handbook (i.e. Overpayments Established by Cause may be reported or validated over a two year period). Each record must have enough elements to allow the record to be established as reportable, attributed to a particular claimant or employer, and classified into the report cells being validated. As a result, traditional response rate issues do not arise in UI DV. However, states may not complete UI DV or submit reports timely for any of several reasons. See B-3, below.
Because UI DV’s scope is very extensive, different sample designs are used for efficiency, to reduce the need for large samples required to estimate a specific proportion of incorrect transactions in the population. The sample types and their logic are as follows. Table B-1 gives the range of samples drawn for Benefits validation described below in further detail. Validation of Benefits populations requires random sampling, which the DV software is programmed to perform automatically. Tax validation relies on an elaborate series of logic tests in building the extract file, supplemented by sorts and two-case samples to ensure that the extract file is built properly. Validation of Tax populations is performed with minimum samples. For both benefits and tax, all logic tests, sorts and samples for an extract file must be passed before the reconstructed count can be considered the valid standard for judging reported counts and thus that the reported counts can pass validation. In addition to the validation of 16 Benefits populations and 5 Tax populations, DV also has separate modules for quality for Benefits and Tax; separations, non-separations, and appeals timeliness and quality is known as Module 4 BTQ; and employer status and field audits tax performance is known as Module 4 TPS; and the review of wage records from employers by submission type is known as wage item validation or Module 5. These separate modules also use a random sampling design.
Populations for both Benefits and Tax are broken down further into mutually exclusive “subpopulations” or a record or transaction with a distinguishing criteria into which all records can be classified and determines which report cell the record is used to validate. The number of subpopulations varies widely; most of the appeals populations only have two subpopulations: one for single claimants and one for multi-claimants. Others, like payments, have dozens that are characterized by program type, claim type, and type of compensation (first payment, continued payment, adjustment, etc).
Random Samples. In Benefits validation, the State draws 18 random samples for the most important types of reports data, e.g., those used to determine administrative funding or build key performance measures. Between six and eighteen data elements are evaluated for each case in the random samples. Although random samples of 100 or 200 cases are drawn, only 30 or 60 cases are evaluated initially as acceptance samples; only if the result of the initial acceptance sample is inconclusive is the entire sample evaluated to estimate the underlying error rate. For benefits extract files to pass—i.e., be considered reliable--all random samples must pass within the 5% error rate; passing supplemental samples is not a criterion for reliability.
Supplemental Samples for Missing Subpopulations. These are samples of one transaction from any subpopulations not represented in the random samples of the broader populations which conceptually include them. These subpopulations could be any of the subpopulations that are assessed as part of DV, but would only be included if they did not appear as a part of the random sample. A complete listing of subpopulations that could provide a supplemental sample can be found in Appendix A in the Benefits section of Handbook 361. These are reviewed simply to check that validation files are programmed properly by determining that the only reason the examined sample did not include a representative from the missing subpopulation is sampling variability–probability that the relatively small random samples may not include rare combinations of elements in the population
Supplemental Samples to Examine Data Outliers. Outliers are only used as supplemental samples when the population has an aging/time lapse or dollar amount component. As an example, a potential sample would look at the 5 oldest and youngest appeals decisions or 5 highest and lowest first payment levels made. This type of sample would only apply to select subpopulations, as shown below in Table B-1. The random and supplemental samples ensure that the population as a whole was defined properly but probably do not assess whether time-lapse measures or dollar transactions contain extreme values. UI DV addresses this issue by sorting those populations and examining the five highest and five lowest values in each sorted population to ensure that there are no calculation and data errors. Although DV refers to these as “samples” they are technically the selection of specific elements.
Supplemental Minimum Samples. UI DV draws no random samples for some transactions considered of lower priority. UI DV simply ensures that the reporting software uses the correct field in the database to process and report the transactions. This is done by randomly selecting two cases per subpopulation. All tax samples are two cases per subpopulation and for a tax extract file to be considered reliable, all sample cases from it must pass. For example, Benefits populations 6 and 7 (Appeals Filed, Lower and Higher Authority, respectively) have no random samples because the universe of transactions from which the extract files are built are too small to reliably draw random samples. Instead, DV examines two records from each subpopulation that make up the population to ensure accuracy; in this example, the state would investigate two single claimant and two multi-claimant appeals filed at each appeal level to satisfy DV.
TABLE B-1
Benefits Population |
Sample Name |
Sample Type |
Size |
||
Number |
Type of Transaction |
|
|
How Selected |
Total |
1 |
Weeks Claimed |
Intrastate Weeks Claimed |
Random |
60/200 |
60/200 |
Interstate Liable Weeks Claimed |
Random |
30/100 |
30/100 |
||
Inter Weeks Claimed filed fr Agent |
Minimum |
2 per subpop |
6 |
||
2 |
Final Payments |
Final Payments |
Random |
30/100 |
30/100 |
3 |
Claims |
New Intra & Inter Liable Claims |
Random |
60/200 |
60/200 |
New Intra & Inter Liable Claims |
Missing Subpops |
1 per subpop |
≤17 |
||
Interstate Filed from Agent |
Minimum |
2 per subpop |
6 |
||
Interstate Taken as Agent |
Minimum |
2 per subpop |
6 |
||
Intra and Inter Transitional Claims |
Random |
30/100 |
30/100 |
||
CWC Claims |
Random |
30/100 |
30/100 |
||
CWC Claims |
Missing Subpops |
1 per subpop |
≤5 |
||
Monetary Sent w/o New Claim |
Minimum |
2 per subpop |
12 |
||
Entering Self Employment Pgm |
Minimum |
2 |
2 |
||
3a |
Additional Claims |
Intrastate Additional Claims |
Random |
30/100 |
30/100 |
Interstate Liable Additional Claims |
Minimum |
2 per subpop |
6 |
||
4 |
Payments |
First Payments |
Random |
|
60/200 |
First Payments |
Missing Subpops |
1 per subpop |
≤15 |
||
First Payments: Intrastate Outliers |
Outliers (TL) |
5 highest, 5 lowest |
10 |
||
Continued Weeks total Payments |
Outliers (TL) |
5 highest, 5 lowest |
10 |
||
Continued Weeks Partial Payments |
Random |
30/100 |
30/100 |
||
Adjusted Payments |
Outliers ($) |
5 highest, 5 lowest |
10 |
||
Self-Employment Payments |
Minimum |
2 |
2 |
||
CWC First Payments |
Random |
30/100 |
30/100 |
||
CWC Continued Payments |
Minimum |
2 per subpop |
4 |
||
CWC Adjusted Payments |
Minimum |
2 per subpop |
4 |
||
CWC Prior Weeks Compensated |
Minimum |
2 per subpop |
4 |
||
5 |
Nonmonetary Determinations |
Single Claimant Nonmon Dets |
Random |
30/100 |
30/100 |
Single Claimant Nonmon Dets |
Missing Subpops |
1 per subpop |
≤59 |
||
Single Claimant Nonmon Dets |
Outliers (TL) |
5 highest, 5 lowest |
10 |
||
UI Multi-Claimant Determinations |
Minimum |
2 per subpop |
8 |
||
Single Claimant Redeterminations |
Random |
30/100 |
30/100 |
||
6 |
Appeals Filed, Lower Authority |
Appeals Filed, Lower Authority |
Minimum |
2 per subpop |
4 |
|
Appeals Filed, Higher Authority |
Appeals Filed, Higher Authority |
Minimum |
2 per subpop |
4 |
8 |
Lower Authority Appeals Decisions |
Lower Authority Appeals Decisions |
Random |
60/200 |
60/200 |
Lower Authority Appeals Decisions |
Missing Subpops |
1 per subpop |
≤21 |
||
Lower Authority Appeals Decisions |
Outliers (TL) |
5 highest, 5 lowest |
10 |
||
9 |
Higher Authority Appeals Decisions |
Higher Authority Appeals Decisions |
Random |
30/100 |
30/100 |
Missing Subpops |
1 per subpop |
≤ 9 |
|||
Outliers (TL) |
5 highest, 5 lowest |
10 |
|||
10 |
Appeals Case Aging, Lower Authority |
Appeals Case Aging, Lower Auth |
Outliers (TL) |
5 highest, 5 lowest |
10 |
11 |
Appeals Case Aging, Higher Authority |
Appeals Case Aging, Higher Auth |
Outliers (TL) |
5 highest, 5 lowest |
10 |
12 |
Overpayments Established by Cause
|
Overpayment $ Established |
Random |
60/200 |
60/200 |
Overpayment $ Established |
Missing Subpops |
1 per subpop |
≤13 |
||
Overpayment $ Established |
Outliers ($) |
5 highest, 5 lowest |
10 |
||
13 |
Overpayment Reconciliation Activities |
Overpayment Reconciliation Activities |
Random |
30/100 |
30/100 |
Overpayment Reconciliation Activities |
Missing Subpops |
1 per subpop |
≤33 |
||
Overpayment Reconciliation Activities |
Outliers ($) |
5 highest, 5 lowest |
10 |
||
14 |
Aged Overpayments |
Aged Overpayments |
Random |
30/100 |
30/100 |
Aged Overpayments |
Missing Subpops |
1 per subpop |
≤11 |
||
Aged Overpayments |
Outliers ($) |
5 highest, 5 lowest |
10 |
||
15 |
Overpayments Established by Mode of Detection |
Overpayment $ Established |
Random |
60/200 |
60/200 |
Overpayment $ Established |
Missing Subpops |
1 per subpop |
≤14 |
||
Notes: This table is from the UI DV Benefits Handbook 361, Appendix A.
The software draws the larger number of Random samples; the first 30 or 60 are investigated as acceptance samples and the remaining 70/140 are only investigated if needed to produce an estimate after an ambiguous result.
Software selects Missing Subpopulation samples on the basis of subpopulations represented in the full 100-case or 200-case draw. Not all subpopulations may be investigated if only first 30 or 60 cases of random sample are reviewed.
Outlier samples may be based on sorts by time lapse (TL), or dollar amount ($).
B-2. Procedures for the collection of information in which sampling is involved.
Statistical methodology for stratification and sample selection for all validations and subpopulations.
B-1 above indicates that 18 samples are “random;” 11 are size 30/100, seven 60/200. The validation software draws samples of 100 or 200, as required; validators evaluate the first 30 of 100 (60 of 200) as acceptance samples. This often results in a clear pass or fail. If ambiguous findings result, the remaining 70 or 140 are evaluated to estimate underlying error rates.
Supplemental samples of size one or two are also drawn from all unrepresented sub-populations to check for the correctness of programming or to ensure that reporting software uses the correct fields in the database.
To check for extreme (outlying) values, the 5 highest and 5 lowest values in report elements classified by time lapse (e.g., 7 days and under, 8-14 days, over 70 days) or report fields containing dollars are evaluated.
Estimation Procedure
Validators must determine whether each underlying population error rate is 5%.
The DV procedure specifies selection of random samples of 100 or 200, depending on the importance of the underlying transactions.
The validator uses a sequential review procedure. The first 30 of the full 100, (or 60 of 200), sampled transactions are checked against agency documentation and the number of errors (i.e., those which fail to conform to Federal definitions) are noted.
The first sequence treats the sampled transactions as acceptance samples of size 30 or 60 to determine whether a judgment can be made at that level or whether review of the remaining cases in the sample is called for. If the result is inconclusive, or the State wishes to estimate the probable underlying error in a population that has clearly failed in the first stage, the additional 60 or 140 sampled transactions are verified and a judgment is made from the 100- or 200-case estimation sample.
The first stage procedure uses the following decision rules:
Pass Fail Inconclusive
30 Cases 0 errors 5 1 - 4 errors
(evaluate remaining 70 cases)
60 Cases 0 errors 7 1 - 6 errors
(evaluate remaining 140 cases)
These decision rules (as well as those below for the full sample) assume that the samples of transactions are selected without replacement from a large population, and that each transaction in a sampled population of transactions has an equal chance of being selected into the main sample of 100 or 200 and into the subsample of 30 or 60 that is used for the first stage. Based on these assumptions, the probabilities of any process passing or failing are computed using the binomial formula.2 The tables below were prepared for the Department by statisticians of Mathematica Policy Research (MPR) in the late 1990s and updated at BLS request in 2004. The Department does not have MPR’s program or the spreadsheet that generated them. The 2004 memo from MPR statistician John Hall and associates explaining their methodology is attached.
Degree of Accuracy Needed for Purpose Described in the Justification.
The basic standard is that an extract file is considered reliable if no more than 5% of the underlying records are invalid, i.e., contain one more data elements that do not conform to Federal definitions If the error rate is above 5%, the State’s reported counts are considered invalid even if the reported count equals the reconstructed count because the reconstructed count cannot be assumed to be the standard for comparison.. This means the State will have to take action to correct the extract file, either by selecting elements differently or correcting the data in the database. The sampling procedure must balance the costs of conducting the validation review against the risks of (a) taking an unwarranted and probably expensive action to correct a process whose true underlying error rate is less than 5% and (b) allowing reporting errors to continue by failing to detect underlying populations whose error rates exceed 5%. The Department only requires a state to take action on the basis of the evidence of a random sample; the non-random benefits samples described in B-1 above provide diagnostic information but the Department does not require states to act on the findings.
The decision rules for the first stage are based on minimizing the chances of failing a sample when the true error rate is acceptable (≤ 0.05). In the first stage, a process passes only with zero errors, and fails if it has 5 or more errors (n = 30) or 7 or more errors (n = 60). To find these cut-off points (pass, fail)
for the first stage, we calculate the Type I and Type II error
contributed from the first stage based on the Binomial distribution
with the actual error rate
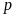 =
0.05.2 The cut-off for
failing at the first stage is labeled C1.
=
0.05.2 The cut-off for
failing at the first stage is labeled C1.
To minimize the Type II error contributed from the first stage we require that there be no error at all to pass the test at the first stage.
To find the
optimal cutoff (C1),
we compared Type I errors for different levels of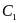 .
The larger
.
The larger
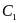 is,
the smaller the type I error is. We want to choose
is,
the smaller the type I error is. We want to choose
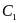 such
that the Type I error (
such
that the Type I error (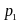 )
)
- is below the 0.05 threshold; and
- is not too close to 0.05 (or too close to 0)
Table 1 gives
the type I errors contributed from stage one upon different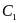 ’s.
From the table we can see that: for the sample size n1 of
30, Type I error would be larger than 0.05 if we choose
’s.
From the table we can see that: for the sample size n1 of
30, Type I error would be larger than 0.05 if we choose
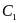 at
4. On the other hand, partial Type I error would be too small if we
choose
at
4. On the other hand, partial Type I error would be too small if we
choose
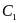 at
6. At
at
6. At
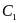 =5,
it is 0.01564, a reasonable number given the criteria above. Hence
we decide that the optimal cutoff for n1=30 is 5 and
similarly the optimal cutoff for n1=60 is 7.
=5,
it is 0.01564, a reasonable number given the criteria above. Hence
we decide that the optimal cutoff for n1=30 is 5 and
similarly the optimal cutoff for n1=60 is 7.
______________________
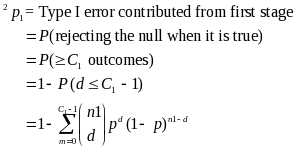
where d is the number of errors

since for any event d, since 0! = 1 and p0 = 1,
 Table
1: Type I Errors from Stage One Upon Different Cutoffs at the First
Stage
Table
1: Type I Errors from Stage One Upon Different Cutoffs at the First
Stage
|
n1=30 |
|
n1=60 |
||||
P |
|
|
|
|
|
|
|
0.01 |
0.00022 |
0.00001 |
0 |
|
0.00003 |
0 |
0 |
0.02 |
0.00289 |
0.00030 |
0.000025 |
|
0.00127 |
0.00020 |
0.00003 |
0.03 |
0.01190 |
0.00185 |
0.000233 |
|
0.00914 |
0.00210 |
0.00042 |
0.04 |
0.03059 |
0.00632 |
0.001061 |
|
0.03251 |
0.00989 |
0.00262 |
0.05 |
0.06077 |
0.01564 |
0.003282 |
|
0.07872 |
0.02969 |
0.00979 |
Failure occurs when the number of errors is at least C1 = 5 for n1 = 30 and 7 when n1 = 60). So the probability of failing can be expressed as 1 minus the probability of not failing where the probability of not failing is the cumulative probability of having fewer than ci errors.3 The probability of passing at the first stage is the probability of having zero errors. The probabilities of failing in the first stage when the true error rate is ≤ 0.05 and of passing at the first stage if the true error rate is > 0.05 are shown in the following two tables.
Probability of Failing When the Error Rate is ≤ 0.05 (Type I error for first stage of sequential sample)
True Error Rate n1= 60 n1= 30

0.01 <.001 <.001
0.02 <.001 <.001
0.03 .002 .002
0.04 .010 .006
0.05 .030 .016
Probability of Passing When the Error Rate is > 0.05 (Type II error for first stage of double sample)
True Error Rate n1= 60 n1= 30

0.05 .046 .215
0.06 .024 .156
0.07 .013 .113
0.08 .007 .082
0.09 .003 .059
0.10 .002 .042
As noted, if the result is inconclusive, the State must evaluate the additional 60 or 140 sampled transactions and make a judgment from the 100- or 200-case estimation sample. (The State may also wish do this to estimate the probable underlying error in a population which has clearly failed in the first stage.)
In the first stage, the methodology emphasizes avoiding Type II error. In the second stage, it is structured to avoid Type I error. The cut-offs are set to ensure that if the underlying error rate is less than or equal to 5%, the probability that a sample will fail is < .05. If the underlying error rate is greater than 5%, probability that a sample will fail is > .05 and increases as the underlying rate increases. The Type I error and power probabilities are summarized in Table 2.
Thus the second stage decision rule is as follows:
Conclude Error Rate is
5% >5%
Expanded Sample 100 9 errors 10+ errors
Expanded Sample 200 16 errors 17+ errors
In the second stage, there are only two outcomes: reject or fail to
reject, so we only need to compute the probability of rejecting the
null hypothesis knowing the true error rate is .
This probability is the probability of Type I error when the
null hypothesis is true and is the power of the test when the null
hypothesis is false.4
.
This probability is the probability of Type I error when the
null hypothesis is true and is the power of the test when the null
hypothesis is false.4
The
value of the second stage failure cut-offs
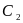 , is
that where conditional on Type I error being below the 0.05
threshold,
, is
that where conditional on Type I error being below the 0.05
threshold,
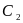 is
such that the power of the test is the largest. Table 2 gives the
Type I error and the power of the test for some potential cutoffs.
From the table we can see that the optimal cutoff for 30/70 sample
is 10 and the optimal cutoff for 60/140 sample is 17.
is
such that the power of the test is the largest. Table 2 gives the
Type I error and the power of the test for some potential cutoffs.
From the table we can see that the optimal cutoff for 30/70 sample
is 10 and the optimal cutoff for 60/140 sample is 17.
_______________________
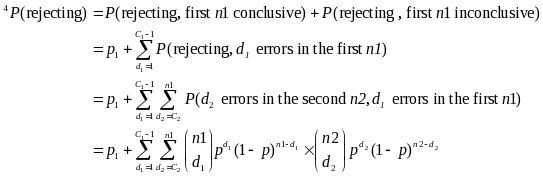
Table 2: Type I Error and Power of the Test Upon Different Cutoffs in the Second Stage
Type I error
|
n =100 |
|
n =200 |
||||
P |
|
|
|
|
|
|
|
|
Type I error |
|
Type I error |
||||
0.01 |
0.000012 |
0.000012 |
0.000012 |
|
0.000002 |
0.000002 |
0 |
0.02 |
0.000465 |
0.000329 |
0.000305 |
|
0.000198 |
0.000196 |
0.00020 |
0.03 |
0.004622 |
0.002568 |
0.002015 |
|
0.002419 |
0.002196 |
0.00213 |
0.04 |
0.022540 |
0.011884 |
0.008021 |
|
0.015451 |
0.012147 |
0.01075 |
0.05 |
0.068876 |
0.038260 |
0.024241 |
|
0.064142 |
0.047050 |
0.03789 |
|
Power |
|
Power |
||||
0.05 |
0.06888 |
0.03826 |
0.02424 |
|
0.06414 |
0.04705 |
0.03789 |
0.06 |
0.15310 |
0.09279 |
0.05930 |
|
0.17911 |
0.13402 |
0.10470 |
0.07 |
0.27197 |
0.18072 |
0.12097 |
|
0.36030 |
0.28608 |
0.22917 |
0.08 |
0.41082 |
0.29735 |
0.21151 |
|
0.56559 |
0.47959 |
0.40341 |
0.09 |
0.55088 |
0.42973 |
0.32548 |
|
0.74364 |
0.66785 |
0.59150 |
0.10 |
0.67648 |
0.56208 |
0.45148 |
|
0.86768 |
0.81414 |
0.75353 |
To compute the overall probability that the sample passes, one must take into account the ways in which the sample can pass. We denote the number of errors in the first stage as d1 and the number from the second stage as d2, and the cut-off for the first sample as c1i and for the second as c2i. The smaller sample (30/70), where c1 = 5 and c2 = 10, can pass in any of five ways:
d1 = 0,
d1 = 1 and d2 < 9
d1 = 2 and d2 < 8
d1 = 3 and d2 < 7
d1 = 4 and d2 < 6
For the larger sample, (60/140) the ways the sample can pass follow the same pattern. More generally, the sample will pass if:
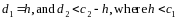
Given this, we can compute the probability of passing for any underlying error rate, as:
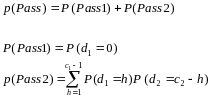
The joint results of the two-stage process produce the following probabilities for the two sample sizes:
Failing a Measure that Should Fail Failing a Measure that Should Pass
Error Rate .10 .09 .08 .07 .06 .05 .05 .04 .03 .02 .01
Sample
30/70 .56 .43 .30 .18 .09 .04 .04 .01 .00 .00 .00
60/140 .81 .67 .48 .29 .13 .05 .05 .01 .00 .00 .00
States that fail may wish to examine a confidence region for their observed error rates. In the case where only the initial sample (30 or 60) has been examined, construction of a confidence region is straightforward. Where the full sample (n = 100 or 200) has been examined, the process is more complex. Below, lower confidence bounds are presented for states to use. Lower bounds are presented instead of confidence intervals, because states with high observed error rates are more likely to find this measure of sampling error useful.6
As discussed above, in determining whether a sample passed or failed the states will test for each sample the null hypothesis that the true error rate is less than or equal to 0.05. Constructing a lower confidence bound for an observed error rate (p*) is analogous to the pass/fail determination. It can be thought of as testing a hypothesis. However, to construct the confidence bound, the test is of a different hypothesis: the true error rate equals the one observed (i.e., p=p*) versus the alternative that the true error rate is less. Thus, the procedures for finding a lower confidence limit are analogous to those in determining the pass or fail cut-off points.
For constructing the confidence bounds the initial samples (n = 30 or 60) can be treated as simple random samples with size n1 from a Binomial distribution.
Therefore
for an observed number of errors do
the corresponding lower confidence bound is determined by finding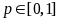 ,
such that
,
such that
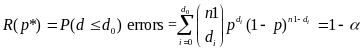
_______________________
6Confidence intervals or sets do not seem to be covered in industrial quality control, where the sequential sampling procedures described in this section are often used. In these settings, the concern is only with whether the batch or sample passed or failed, not with the precision of the observed error rate.
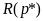 is a decreasing function of
is a decreasing function of
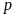 . For
example, when n1=30 and do=4,
(p* = .133). For
. For
example, when n1=30 and do=4,
(p* = .133). For
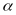 =0.05,
the corresponding solution is 0.069 so the lower 95 percent bound
would be 0.069.
=0.05,
the corresponding solution is 0.069 so the lower 95 percent bound
would be 0.069.
The following table gives the lower 95% confidence bound for n1=30 and n1=60 respectively.
Table 3: The Lower Confidence Bound for Simple Random Sampling
|
n1 = 30 |
|
n1 = 60 |
|||||
Errors |
Error Rate |
Lower Bound (95%) |
|
Errors |
Error Rate |
|||
0 |
0.000 |
0.002 |
|
0 |
0.000 |
0.002 |
|
0 |
1 |
0.033 |
N/A |
|
1 |
0.033 |
N/A |
|
1 |
2 |
0.067 |
N/A |
|
2 |
0.067 |
N/A |
|
2 |
3 |
0.100 |
N/A |
|
3 |
0.100 |
N/A |
|
3 |
4 |
0.133 |
N/A |
|
4 |
0.133 |
N/A |
|
4 |
5 |
0.167 |
0.091 |
|
5 |
0.167 |
0.091 |
|
5 |
6 |
0.200 |
0.115 |
|
6 |
0.200 |
0.115 |
|
6 |
7 |
0.233 |
0.141 |
|
7 |
0.233 |
0.141 |
|
7 |
8 |
0.267 |
0.167 |
|
8 |
0.267 |
0.167 |
|
8 |
9 |
0.300 |
0.194 |
|
9 |
0.300 |
0.194 |
|
9 |
10 |
0.333 |
0.222 |
|
10 |
0.333 |
0.222 |
|
10 |
11 |
0.367 |
0.250 |
|
11 |
0.367 |
0.250 |
|
11 |
12 |
0.400 |
0.279 |
|
12 |
0.400 |
0.279 |
|
12 |
13 |
0.433 |
0.309 |
|
13 |
0.433 |
0.309 |
|
13 |
14 |
0.467 |
0.339 |
|
14 |
0.467 |
0.339 |
|
14 |
15 |
0.500 |
0.370 |
|
15 |
0.500 |
0.370 |
|
15 |
16 |
0.533 |
0.402 |
|
16 |
0.533 |
0.402 |
|
16 |
17 |
0.567 |
0.434 |
|
17 |
0.567 |
0.434 |
|
17 |
18 |
0.600 |
0.467 |
|
18 |
0.600 |
0.467 |
|
18 |
19 |
0.633 |
0.501 |
|
19 |
0.633 |
0.501 |
|
19 |
20 |
0.667 |
0.535 |
|
20 |
0.667 |
0.535 |
|
20 |
For n1 = 30, 1 to 4 errors in the first sample will result in the second-stage sample (n2 = 70) being selected and for n1 = 60, 1 to 6 errors will result in the second-stage sample (n2 = 140) being selected. Because in these instances the error rate will be based on the full sample (n=100 or n= 200), the lower confidence limits will be found in Table 5, and hence they are designated as N/A in this table.
When both samples are used, errors are observed from both samples and the samples are not independently selected (the second sample is used only if the first sample is inconclusive). So to construct a lower bound for this case we begin in a manner analogous to setting the cut off points for failing when the purpose is to determine whether the sample passes or fails.
Thus, the lower bound is the smallest value of
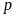 such
that:
such
that:
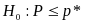
is accepted (p* is the observed error rate). With this criterion, one can define a decision rule for the sequential sampling. (The method for the decision rule has already been illustrated above.) For example for the 30/70 sample, Table 4 gives the optimal cutoff for some illustrative error rates.
Table 4: The Optimal Cutoff for p* in Sequential Sampling
n1 = 30 |
|
n1 = 60 |
||||
P |
C1 |
C2 |
|
P |
C1 |
C2 |
0.06 |
6 |
11 |
|
0.06 |
7 |
20 |
0.07 |
6 |
13 |
|
0.07 |
9 |
22 |
0.08 |
6 |
15 |
|
0.08 |
10 |
24 |
0.09 |
7 |
15 |
|
0.09 |
11 |
26 |
0.10 |
7 |
17 |
|
0.10 |
12 |
29 |
0.15 |
9 |
23 |
|
0.15 |
15 |
41 |
0.20 |
11 |
29 |
|
0.20 |
19 |
52 |
For each observed pair of errors, the lower 95% confidence bound is
the first
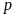 that
the null hypothesis is going to be accepted upon this
that
the null hypothesis is going to be accepted upon this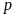 .
For example, if there are 2 errors in the first stage and 5 errors
overall, the smallest
.
For example, if there are 2 errors in the first stage and 5 errors
overall, the smallest
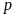 such
that the null is accepted upon
such
that the null is accepted upon
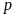 is
0.020. Table 5 gives the 95 percent lower bound for the case where
both samples are used.
is
0.020. Table 5 gives the 95 percent lower bound for the case where
both samples are used.
Unusual Problems Requiring Specialized Sampling Procedures
The discussion above indicates that the methodology uses specialized sampling procedures. Strictly speaking, none of these are required. However, because of the scope of UI DV, they are employed for efficiency. Most State UI management information systems are highly automated, and States are able to obtain most data elements they report to the Department of Labor as a byproduct of their ongoing functions of paying benefits and collecting taxes. Thus, the greatest risks to report validity are from systematic errors–incorrectly programmed functions which miss certain elements, double count other elements, obtaining counts of transactions which do not meet the Federal reporting requirements for the element being reported, or programming which
Table 5: The Lower (95%) Confidence Bound for Sequential Sampling
Errors |
N=30/70 |
N=60/140 |
||||
Total |
From n1 |
From n2 |
Error Rate |
Lower Confidence Bound |
Error Rate |
Lower Confidence Bound |
1 |
1 |
0 |
0.010 |
0.002 |
0.005 |
0.001 |
2 |
1 |
1 |
0.020 |
0.002 |
0.010 |
0.001 |
2 |
2 |
0 |
0.020 |
0.010 |
0.010 |
0.005 |
3 |
1 |
2 |
0.030 |
0.009 |
0.015 |
0.005 |
3 |
2 |
1 |
0.030 |
0.010 |
0.015 |
0.005 |
3 |
3 |
0 |
0.030 |
0.023 |
0.015 |
0.012 |
4 |
1 |
3 |
0.040 |
0.015 |
0.020 |
0.008 |
4 |
2 |
2 |
0.040 |
0.015 |
0.020 |
0.008 |
4 |
3 |
1 |
0.040 |
0.023 |
0.020 |
0.012 |
4 |
4 |
0 |
0.040 |
0.040 |
0.020 |
0.020 |
5 |
1 |
4 |
0.050 |
0.020 |
0.025 |
0.010 |
5 |
2 |
3 |
0.050 |
0.020 |
0.025 |
0.010 |
5 |
3 |
2 |
0.050 |
0.023 |
0.025 |
0.012 |
5 |
4 |
1 |
0.050 |
0.040 |
0.025 |
0.020 |
6 |
1 |
5 |
0.060 |
0.027 |
0.030 |
0.014 |
6 |
2 |
4 |
0.060 |
0.027 |
0.030 |
0.014 |
6 |
3 |
3 |
0.060 |
0.027 |
0.030 |
0.014 |
6 |
4 |
2 |
0.060 |
0.040 |
0.030 |
0.020 |
7 |
1 |
6 |
0.070 |
0.033 |
0.035 |
0.017 |
7 |
2 |
5 |
0.070 |
0.033 |
0.035 |
0.017 |
7 |
3 |
4 |
0.070 |
0.033 |
0.035 |
0.017 |
7 |
4 |
3 |
0.070 |
0.040 |
0.035 |
0.020 |
8 |
1 |
7 |
0.080 |
0.038 |
0.040 |
0.019 |
8 |
2 |
6 |
0.080 |
0.038 |
0.040 |
0.019 |
8 |
3 |
5 |
0.080 |
0.038 |
0.040 |
0.019 |
8 |
4 |
4 |
0.080 |
0.041 |
0.040 |
0.020 |
9 |
1,2,3,4 |
8,7,6,5 |
0.090 |
0.047 |
0.045 |
0.024 |
10 |
1,2,3,4 |
9,8,7,6 |
0.100 |
0.053 |
0.050 |
0.027 |
11 |
1,2,3,4 |
10,9,8,7 |
0.110 |
0.058 |
0.055 |
0.031 |
12 |
1,2,3,4 |
11,10,9,8 |
0.120 |
0.069 |
0.060 |
0.034 |
13 |
1,2,3,4 |
12,11,10,9 |
0.130 |
0.075 |
0.065 |
0.037 |
14 |
1,2,3,4 |
13,12,11,10 |
0.140 |
0.080 |
0.070 |
0.042 |
15 |
1,2,3,4 |
14,13,12,11 |
0.150 |
0.092 |
0.075 |
0.046 |
16 |
1,2,3,4 |
15,14,13,12 |
0.160 |
0.098 |
0.080 |
0.049 |
17 |
1,2,3,4 |
16,15,14,13 |
0.170 |
0.110 |
0.085 |
0.054 |
18 |
1,2,3,4 |
17,16,15,14 |
0.180 |
0.116 |
0.090 |
0.057 |
19 |
1,2,3,4 |
18,17,16,15 |
0.190 |
0.123 |
0.095 |
0.060 |
20 |
1,2,3,4 |
19,18,17,16 |
0.200 |
0.134 |
0.100 |
0.066 |
reflects a misinterpretation of Federal reporting requirements. Systematic problems normally affect all elements in a population grouping, so the examination of just a few is sufficient to identify the problem. A larger, random sample would of course identify the same problem but at much higher cost. Similarly, large random samples would probably detect the existence of outliers in time lapse data or data involving the reporting of dollar amounts. However, small samples of transactions from the extremes of an arrayed distribution do it much more efficiently.
Use of Periodic Data Collection to Reduce Burden
UI DV employs a 3-year cycle to reduce burden. Only the components that fail validation (a discrepancy between a reported count and a reconstructed count greater than 2%, or quality samples showing more than a 5% rate of invalid cases in the population examined) must be revalidated in the following year.
If a state does not submit validation results for a population and that population is due, it is counted as a “fail” and must be validated in the following year.
The exception is the report cells used to calculate Government Employment and Results Act measures. These must be validated annually, and the reported count must be within ±1% of the reconstructed count. This currently applies to two Benefits populations (4 and 12) and one Tax population (3).
B-3. Methods to Maximize Response Rates.
Although this collection is based on agency records, our experience to date does indicate non-response in the sense that some states have not been able to complete all or part of data validation. In some cases, state resources have precluded them from doing all or part of DV. In others, they have deferred part of DV pending the installation of new administrative data systems. There have been a few instances where the validation methodology cannot be applied because the state reports are not automated, or the state validators have concluded that their reports cannot pass validation or be completely validated because their data systems lack key information, e.g., the date a receivable was established. In all these instances, states are required to include corrective action plans to complete implementation of UIDV or to fix their reports and submit their UI DV reports as part of their annual performance management and budgeting plan (called the State Quality Service Plan). In the course of validations, states often discover that the documentation for certain reported transactions--e.g., nonmonetary determinations or benefit appeals--is missing. In considering which transactions have been reported accurately, validation does not distinguish between missing documentation and other forms of errors; an inadequately documented transaction is considered an error.
We expect that for the Validation Year 2016 period (results submitted by June 10, 2016) all states and territories will submit DV results and the total items submitted will be about 75 percent of what is due, up from 72 percent in VY 2015. In the following year, the total submission rate is expected to normalize and remain current at about 75 percent.
B-4. Tests of Procedures or Methods.
In 1998, three States–Massachusetts, Minnesota, and North Carolina–pilot tested the UI DV methodology. A technical support contractor, who employed as a subcontractor the person who developed the UI DV methodology, provided oversight of the pilot test. The contractor’s evaluation indicated that the methodology functioned as intended and enabled the States to detect, and correct, reporting errors. The cost data from the pilot were the basis for the burden estimates in the original request. In the first three years of authorization, most states have completed at least parts of validation requirements. Burden estimates for this request are based on estimates provided by states that have completed validations, and reflect assumptions consistent with a new software environment.
B-5. Individuals Consulted on Statistical Aspects of the Design
William S. Borden
Senior Fellow
Mathematica Policy Research, Inc.
(609) 275-2321
John Hall
Senior Statistician
Mathematica Policy Research, Inc.
(609) 799-3535
Walter Corson
Senior Fellow
Mathematica Policy Research, Inc.
(609) 799-3535
Alan Dorfman
Senior Mathematical Statistician
Office of Survey Methods Research
Bureau of Labor Statistics
(202) 691-7378
Andrew Spisak
Consulting Statistician
St. Louis & Associates
(571) 481-0450
1 DV is mandatory for all 50 states, as well as the District of Columbia, Puerto Rico and the US Virgin Islands. As a result, States here refers to the 53 total states, territories and jurisdictions that must operate DV.
2The probability of exactly d events (in this case errors) occurring with n trials where the population prevalence of these events is p (in this case the error rate) is expressed as:
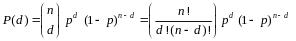
The probability that no more than c events occurring is:
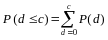
3For a given true error rate (p), the probability of failing is:
1 –P(not failing) = 1 – P(d ≤ C1 – 1)
B-
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Modified | 0000-00-00 |
| File Created | 2021-01-24 |
© 2025 OMB.report | Privacy Policy
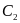 =9
=9