Sampling and Weighting Plan
Att N_Sampling and Weighting Plan v2.docx
2021 and 2023 National Youth Risk Behavior Surveys and 2021 ABES
Sampling and Weighting Plan
OMB: 0920-0493
2021 and 2023 National Youth Risk Behavior Survey
Attachment N
Sampling and Weighting Plan
SAMPLING AND WEIGHTING PLAN
2021 NATIONAL YOUTH RISK BEHAVIOR SURVEY
Submitted to:
Centers for Disease Control and Prevention
Division of Adolescent and School Health
Prepared by:
Ronaldo Iachan
Alice Roberts
Kate Flint
ICF
Introduction
The national Youth Risk Behavior Survey (YRBS) was developed to monitor priority health risk behaviors that contribute to the leading causes of mortality, morbidity, and social problems among youth and young adults in the United States. The YRBS monitors six categories of health risk behaviors:
Behaviors that contribute to unintended injury and violence
Tobacco use
Alcohol and other drug use
Sexual behaviors that contribute to unintended pregnancy and sexually transmitted diseases, including HIV infection
Dietary behaviors
Physical inactivity
The YRBS also monitors the prevalence of obesity and asthma.
The objective of the sampling design is to support estimation of the health risk behaviors in a nationally representative population of 9th through 12th grade students. Estimates will be generated among students overall and by sex, grade, and race/ethnicity (white, black, Hispanic). The 2021 YRBS will be the 16th fielding of this national survey.
Section 2 of this document presents the sampling design, including our plans for achieving the target number of participating students in the 2021 national YRBS. Section 3 describes the sampling methods planned for the surveys. Section 4 presents the planned weighting and variance estimation procedures.
Estimation and Justification of Sample Size
Overview
The sample design proposed for the 2021 YRBS survey is consistent with the sample design used in past cycles, which includes adjusting sampling parameters to reflect changing demographics of the in-school population of high school students.
The YRBS sample size calculations are based on the following assumptions:
The main structure of the sampling design will be consistent with the design used to draw the sample for prior cycles of the YRBS.
3 Secondary Sampling Units (SSUs) within each sample Primary Sampling Unit (PSU) will be selected. A PSU is defined as a county, a portion of a county, or a group of counties. A SSU is a “full” school that serves as a sampling unit that can supply a full complement of students in grades 9 through 12. SSUs with at least 28 students per grade are considered “large;” otherwise they are considered “small.” On average, each selected class will include 28 students.1
A 63% overall response rate, the average over the past five cycles, calculated as the product of the school and student response rates.
Based on these assumptions, we will draw a sample of 54 PSUs, with 3 large SSUs (“full” schools) selected from each PSU for a total of 162 SSUs. On average, a PSU will supply a sample of 336 students across all of grades 9-12 before non-response (3 SSUs * 4 grades/school * 28 students per grade). The estimated sample yield from these large schools will be 18,144 students before school and student non-response.
To provide adequate coverage of students in small schools (those with an enrollment of less than 28 students in any grade) we also will select small SSUs from a subsample of 15 PSUs. As in prior YRBS cycles, we will select one small SSU in each of 15 subsample PSUs, therefore adding an additional 15 SSUs to the sample. From historical averages, small SSUs are expected to add 1,000 students before non-response.
Therefore, the proposed sample design is expected to yield 177 SSUs. SSUs are either comprised of a single school (if the school includes each of grades 9-12), or is created by linking two or more physical schools that do not include all of grades 9-12. This is done to form school-based SSUs that provide coverage for all four grades in each unit. During the grade selection process (see section 2.5.1), physical schools are selected for each SSU. We expect 200 physical schools in a sample of 177 SSUs. These schools are expected to yield in total 19,144 selected students and 12,067 participating students using an average 63% overall response rate.
Within each school, one class will be selected from each grade to participate in the survey except in high minority schools, where two classes per grade will be selected. Double class selection has been used in all previous YRBS surveys to support health risk behavior prevalence estimates by race/ethnicity. For the 2021 YRBS, we will implement double class selection in schools with higher concentrations of black student enrollment. As discussed later in Section 3.4.3, the changes have been introduced to enhance the black student yields; i.e., the number of participating black students.
Expected Confidence Intervals
Factors that influence the size of prevalence estimate confidence intervals include 1) whether the estimate is for the full population or for a demographic subgroup (i.e., by sex, race/ethnicity, or grade) 2) the prevalence rate, 3) and the design effect (DEFF) associated with each risk behavior.2 The DEFF, which equals 1.0 for simple random sampling, reflects the variance-increasing effects of unequal weighting and sample clustering.
Based on the prior YRBS studies, which had similar designs and sample sizes, we can expect the following levels of precision:
95% confidence for domains defined by grade, sex, or race/ethnicity;
95% confidence for domains defined by crossing grade or race/ethnicity by sex; and
90% confidence for domains formed by crossing grade with race/ethnicity.
Sampling Methods
The sampling universe for the national YRBS will consist of all regular public, Catholic and other private school students in grades 9 through 12 in the 50 states and the District of Columbia. Alternative schools, special education schools, Department of Defense operated schools, vocational schools that serve only pull-out populations, and students enrolled in regular schools unable to complete the questionnaire without special assistance are excluded.
The sample will be a stratified, three-stage cluster sample with PSU stratified by racial/ethnic status and urban versus rural. PSUs are classified as "urban" if they are in one of the 54 largest Metropolitan Statistical Areas (MSA) in the U.S.; otherwise, they are classified as "rural". Within each stratum, PSUs, defined as a county, a portion of a county, or a group of counties, will be chosen without replacement at the first stage. Exhibit 3.1 presents key sampling design features.
Exhibit 3.1 Key Sampling Design Features
Sampling Stage |
Sampling Units |
Sample Size (Approximate) |
Stratification |
Measure of Size |
1 |
PSU: County, a portion of a county, or a group of counties |
54 PSUs |
Urban vs. non-urban (2 strata) Minority concentration (8 strata)
|
Aggregate school size in target grades |
2 |
Schools |
Sample 200 physical schools (>=3 per PSU)
|
Small vs. other |
Enrollment |
3 |
Classes/ students |
1 or 2 classes per grade per school: Approx. 19,000 selected students Approx. 12,000 participating students |
|
|
Design Updates and Modifications
We plan to replicate the main features of the 2017 and 2019 YRBS sample designs. As in the past few cycles, we will continue to adjust sampling parameters to reflect changing demographics of the in-school population.
Decreasing Need to Oversample Hispanic and Black Students
In general, as the proportion of black and Hispanic students in the study population increases and the minority population becomes more evenly distributed, the parameters that drive minority oversampling can be relaxed, allowing us to maintain yields while moving towards a statistically more efficient design.
Specifically, growing percentages of black and Hispanic students have allowed the design to be closer to a self-weighting design, and therefore, be more efficient in the sense of minimizing the variance of overall survey estimates. The main modification in the last few cycles of the study has been to define the measure of size (MOS) as eligible enrollment rather than a weighted MOS designed to oversample minority students.
In cycles prior to 2017, the allocation to strata oversampled strata with higher concentrations of minority students. In the 2017 and 2019 YRBS, however, the design moved to a nearly proportional allocation, again with the aim of enhancing the precision of overall estimates. The historical data on the concentrations of black and Hispanic students reinforce the finding that oversampling via the weighted MOS is no longer necessary to achieve sufficient numbers of black and Hispanic students. Double class sampling still implements oversampling of black students by focusing this sampling on schools with higher concentrations of black students.
Exhibit 3.2 presents the percentages of public high-school students who are black and Hispanic, respectively, for the years 2008-09, 2009-10, 2010-11, 2011-12, 2015-16, and 2017-18. The table shows that while the percentage of black students has remained stable, the percentage of Hispanic students has been steadily increasing over the last few years. The percentage of Hispanic high-school students has increased from 19.0% in 2008-09 to 23.6% in 2017-18. By contrast, the percentage of black students has declined from 16.9% to 14.87%.
Exhibit 3.2 Historical Trends for Black and Hispanic Students
|
2008-2009 |
2009-10 |
2010-11 |
2011-12 |
2015-16 |
2017-18 |
Black |
16.90% |
16.79% |
16.23% |
15.94% |
12.21% |
14.87% |
Hispanic |
19.04% |
19.88% |
20.99% |
21.72% |
23.58% |
Design Updates
Two other design features are also routinely updated in each cycle:
The stratum boundaries based on the percentage of minority students will be re-computed to minimize variances according to the cumulative square root rule (Dalenius-Hodges rule).3
We will adjust PSU definitions to account for school openings and closings and may also adjust PSU sample sizes by one or two (in either direction) if the simulated yields indicate the need for adjusting sample sizes.
In addition, as described in Section 3.4.3, the PSU sample allocation has been revised to enhance the yields for minority students, and specifically the yield for black students which has declined over the last two cycles.
Frame Creation
In the 2021 YRBS, we will continue the practice of constructing a more comprehensive sampling frame from different data sources. The frame will combine data files obtained from MDR Inc. (Market Data Retrieval, Inc.) and from the National Center for Education Statistics (NCES). The MDR frame contains school information including enrollments, grades, race distributions within the school, district, and county information, and other contact information for public and non-public schools across the nation. The NCES frame source include the Common Core of Data (CCD) for public schools and the Private School Survey (PSS) for non-public schools. Prior to the 2013 YRBS, one single source of national schools (MDR) was used as the sampling frame.
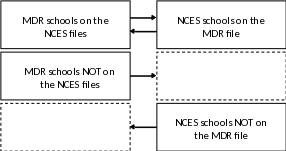
The reason for moving to a frame build from multiple data sources was to increase the coverage of schools nationally. Exhibit 3.3 illustrates the potential increase of coverage. If we consider the column of data on the left to be the previous approach and the column of data on the right to be the added NCES datasets, we can see that both sources of data are missing schools from their list (indicated by the dashed lines). The MDR schools not on the NCES files do not represent an increase in coverage. They already exist on the single-source frame. Combining helps to fill in the missing schools, insuring more representation.
This dual-source frame build method was piloted in 2015 and resulted in a coverage increase among all public and non-public high schools of 23%. There was 15.5% increase of coverage among public schools and a 46% increase in coverage among non-public high schools. The increase of schools increased the student coverage among public high schools by 2% and 16.5% for non-public high schools. Most of the added schools were smaller schools. This dual-source frame build method has subsequently been used each cycle.
Exhibit 3.3 Increased Coverage with the Combined File Approach
When combining data sources to form a sampling frame, it is essential to eliminate duplicates across the files – that is, each school should be represented once on the final frame, regardless of the number of times it is represented in the multiple source files. To minimize duplication, schools will be matched based on NCES school identifier, address and phone number. Once the sample has been drawn a manual review of the sampled schools will be conducted to further eliminate duplicate schools.
School Size Threshold
Another modification introduced in 2015 was the inclusion of a threshold for school size so that the frame does not include very small schools. The threshold is defined in terms of the aggregate school enrollment in eligible grades. The threshold was modified from the minimum 25, used in prior cycles, to a minimum total enrollment of 40. The school size threshold was established in consultation with CDC primarily for cost efficiency, but also due to concerns about confidentiality. The cost of recruiting and collecting data from very small schools outweighed the benefit of adding a relatively small number of students that attend this subset of schools. In other words, the efficiency gains may come at the price of under-coverage of small schools, with the potential for associated biases. This section summarizes the results of our investigation of the under-coverage impact of requiring a minimum school size.4
This analysis looks at the percentage of students that would be left out of the frame for varying values of the threshold. To assess the potential bias that might be associated with these exclusions, we also examine the percentage of black and Hispanic students who are left out of the frame when very small schools are not included in the school frame.5 The analysis shows that the bias potential is very small for either size threshold, c=25 or c=40.
Exhibit 3.4 shows the percent of students omitted from the frame when schools below a given size threshold are dropped. The relative loss is addressed for thresholds of 25 and 40. The exhibit considers the combined frame design used in the recent cycles of the YRBS which captures a larger number of smaller schools. The exhibit shows that 0.51% of the students would have been excluded from the frame using a truncation threshold of 25 students; for a threshold of 40, these percent exclusions go up to 0.97%. The percentages of minority students also drop by very small amounts for the threshold of c=40 as well as for c=25.
Exhibit 3.4. Impact of Removing Very Small Schools from the Frame
Threshold |
Percent of Students Lost |
Percent of Black Students Lost |
Percent of Hispanic Students Lost |
c=25 |
0.51% |
0.44% |
0.30% |
c=40 |
0.97% |
0.83% |
0.56% |
In summary, the truncation resulting from either size threshold leads to small levels of student-level under-coverage, and therefore, minimum impact on student-level estimates. At the same time, excluding these very small schools will lead to substantial efficiencies in recruitment efforts and in increased student yields per visited school. Therefore, ICF plans to continue the use of a threshold of c=40 for the 2021 YRBS.
Measure of Size
The sampling approach will utilize Probability Proportional to Size (PPS) sampling methods. In general, when the measure of size is defined as the count of final-stage sampling units, and a fixed number of units are selected in the final stage of a PPS sample, the result is an equal probability of selection for all members of the universe. This is the case for the YRBS, where student counts are used as the measure of size, and a roughly fixed number of students are selected from each school as the final stage. Thus, this design results in a roughly-self weighting sample.
Prior cycles of YRBS have included a weighted measure of size to increase the probability of selection of high minority (Hispanic and black) PSUs and schools. The effectiveness of a weighted measure of size in achieving oversampling is dependent upon the distributions of black and Hispanic students in schools. The need for a weighted measure of size is predicated on a relatively low prevalence of minority students in the population; however, this premise has become less tenable with the growth in the population proportion of black and Hispanic students as seen in Exhibit 3.2 earlier.
During the design of the initial YRBS cycles, ICF conducted a series of simulation studies that investigated the relationship of various weighting functions to the resulting numbers and percentages of minority students in the obtained samples.6 We performed new simulation studies periodically to ensure that we are using the minimum amount of measure of size weighting necessary to achieve target yields of black and Hispanic students. Starting with the 2013 YRBS, we concluded that we could move to an unweighted measure of enrollment size, which would increase the statistical efficiency of the design and therefore lead to more precise prevalence estimates. Therefore, an unweighted measure of size will continue to be used for the 2021 YRBS sampling designs.
First-stage Sampling
Definition of Primary Sampling Units
In defining PSUs, several issues are considered:
Each PSU should be large enough to contain the requisite numbers of schools and students by grade, and small enough so as not to be selected with near certainty.
Each PSU should be compact geographically so that field staff can go from school to school easily.
PSUs definitions should be consistent with secondary sampling unit (school) definitions.
PSUs are defined to contain at least five large high schools.
Generally, counties will be equivalent to PSUs, with two exceptions:
Low population counties are combined to provide sufficient numbers of schools.
High population counties are divided into multiple PSUs so that the resulting PSU will not be selected with certainty7.
The basic county-to-PSU assignments have remained relatively stable from one YRBS cycle to the next. As we obtain new frame data each YRBS cycle, school and student counts for each PSU are updated to account for school openings and closings.
County population figures will be aggregated from school enrollment data for the grades of interest.
The PSU frame is then screened for PSUs that no longer meet the criteria given above. We adjust the frame by re-combining small counties/PSU as necessary to ensure sufficient size while maintaining compactness. Near certainty PSUs are split using an automated procedure built into the sampling program.
Stratification of PSUs
The PSUs will be organized into 16 strata, based on the urban/rural location of the school and minority enrollment. The approach involves the computation of optimum stratum boundaries using the cumulative square root of “f” method developed by Dalenius-Hodges. This method is useful where there are many PSUs at the lower levels of concentration, and they become sparse as the percentage increases, which is the case here. The boundaries or cutoffs change as the frequency distribution (“f”) for the racial groupings change from one survey cycle to the next.
To reiterate, the three-stage cluster sample will be stratified by racial/ethnic composition and urban versus non-urban status at the first stage. PSUs are defined as a county, a group of smaller counties, or a portion of a very large county. PSUs are classified as “urban” if they are in one of the 54 largest MSAs in the U.S.; otherwise, they are classified as “non-urban.”
Additional, implicit stratification will be imposed by geography by sorting the PSU frame by state and by 5-digit ZIP Code (within state). Within each stratum, a PSU will be randomly sampled without replacement at the first stage.
The specific definitions of primary strata are as follows:
If the percentage of Hispanic students in the PSU exceeded the percentage of black students, then the PSU is classified as Hispanic. Otherwise it is classified as black.
If the PSU is within one of the 54 largest MSAs in the U.S. it is classified as 'Urban', otherwise it is classified as 'Rural.'
Hispanic Urban and Hispanic Rural PSUs are classified into four density groupings depending upon the percentages of Hispanic students in the PSU.
Black Urban and Black Rural PSUs are also classified into four groupings depending upon the percentages of black students in the PSU.
Exhibit 3.5 illustrates the process with preliminary boundaries. It is worth stressing that the boundaries are re-computed for each cycle of the YRBS as we employ the Dalenius-Hodges method (described above) to allow the boundaries to adapt to the changing race/ethnic distribution of the student population.
Exhibit 3.5 Minority Percentage Bounds for PSU stratification
Minority Concentration |
Density Group |
Bounds |
|
Urban |
Rural |
||
Black |
1 |
0%-22% |
0%-18% |
2 |
>22%-34% |
>18%-34% |
|
3 |
>34%-56% |
>34%-58% |
|
4 |
>56%-100% |
>58%-100% |
|
Hispanic |
1 |
0%-22% |
0%-22% |
2 |
>22%-34% |
>22%-44% |
|
3 |
>34%-45% |
>44%-66% |
|
4 |
>45%-100% |
>66%-100% |
|
Allocation of the PSU sample
In the last few cycles of the YRBS, the sample PSUs were allocated to the 16 strata, described in Exhibits 3.5 and 3.6, nearly proportionally to student enrollment. To improve the black student yield, and therefore the precision of subgroup estimates, the allocation will be revised as shown in Exhibit 3.6.
Exhibit 3.6. Sample PSU Allocation to First-Stage Strata
Predominant Minority |
Urban/Rural |
Density Group Number |
Stratum Code |
Original Proportional Allocation |
Revised Allocation
|
Black |
Urban
|
1 |
BU1 |
4 |
4 |
2 |
BU2 |
3 |
3 |
||
3 |
BU3 |
1 |
2 |
||
4 |
BU4 |
1 |
2 |
||
Rural
|
1 |
BR1 |
6 |
5 |
|
2 |
BR2 |
3 |
3 |
||
3 |
BR3 |
2 |
3 |
||
4 |
BR4 |
1 |
2 |
||
Hispanic |
Urban
|
1 |
HU1 |
7 |
6 |
2 |
HU2 |
5 |
4 |
||
3 |
HU3 |
4 |
4 |
||
4 |
HU4 |
3 |
3 |
||
Rural
|
1 |
HR1 |
9 |
7 |
|
2 |
HR2 |
2 |
2 |
||
3 |
HR3 |
2 |
2 |
||
4 |
HR4 |
1 |
2 |
The allocation was developed based on simulations using the 2019 YRBS sampling frame. The simulation results include the projected yields by racial/ethnic subgroup and by grade summarized in Exhibit 3.7. The exhibit confirms that the revised allocation substantially improves the sample sizes projected for black students.
Exhibit 3.7 Projected student subgroup yields under the original and revised allocations
Grade |
Black Yield: ORIGINAL ALLOCATION |
Hispanic Yield: ORIGINAL ALLOCATION |
Black Yield: REVISED ALLOCATION |
Hispanic Yield: REVISED ALLOCATION |
9th |
1123 |
1302 |
1340 |
1623 |
10th |
1130 |
1314 |
1346 |
1641 |
11th |
1125 |
1329 |
1343 |
1653 |
12th |
1114 |
1321 |
1326 |
1663 |
Selection of PSUs
Using PPS sampling, we will select a sample of 54 PSUs for the YRBS. The size measure used will be the sum of total school enrollment across schools in the PSU. With PPS sampling, the selection probability for each PSU is proportional to the PSU’s measure of size.
If
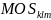 is the measure of size for school k
in PSU l
in stratum m
and if
is the measure of size for school k
in PSU l
in stratum m
and if
 is
the number of PSUs to be selected in stratum m, then
is
the number of PSUs to be selected in stratum m, then
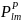 is the probability of selection of PSU l in stratum m:
is the probability of selection of PSU l in stratum m:
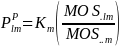
As noted above, 15 of the 54 sample PSUs will be sub-sampled for the separate sampling of small schools. Thus, the sub-sample PSUs are assigned an additional sampling factor (15/54) in their probability of selection for small schools.
Second-stage sampling
Second-stage units (SSUs)
Secondary Sampling Units (SSUs) are formed from single schools or combinations of schools. Single schools represent their own SSU if they have students in each of grades 9th-12th. Schools that do not have all grades are grouped together to form an SSU (a.k.a., “linked school”). Most commonly, students from a 10-12th grade school are grouped with the 9th grade students from a nearby 7th-9th grade school to form a SSU. Forming SSUs that contain all grades ensure representation at each grade level to support the selection of one or more classes from each grade in SSUs (third stage).
Stratification
SSUs are stratified into two size strata comprised of Small and Large schools. Small schools are defined as those that cannot support the selection of an entire class at all grade levels. That is, a school is considered to be small if it has less than 28 students per grade at any grade level; all other schools are considered large.
SSU selection
Three large high schools are selected from each PSU. In addition, one small school is selected from each of 15 sub-sample PSUs. SSUs will be selected using a systematic probability proportional to size (PPS) method, with the unweighted enrollment described earlier as the measure of size.
The probability of selecting
large school k
in PSU l
and stratum m,
 ,
was computed as follows:
,
was computed as follows:

For Small schools, one school
was drawn from sub-sampled PSU, so the probability of selection of a
small school,
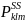 ,
then becomes:
,
then becomes:
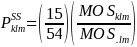
Note that the factor of 15/54 is the fixed probability that the PSU was selected for small school sampling.
Third-stage sampling
Selection of grades
Within large SSUs, a single grade is sampled to represent the school at each of the four high school grades. For the vast majority of SSUs, composed of one physical school, this means that all eligible grades are included in the class selection process for the school; there is a one-to-one correspondence between SSU and school.
Within each SSU formed by linking, or combining physical schools, grade samples are drawn independently with one component school being selected to supply each grade, proportional to grade level enrollment.
For small schools, no grade level sampling is performed. All students in the eligible grades that make up the school will be selected. From historical averages, each small school supplies an expected draw of 63 students per school.
Selection of classes
In schools not designated as high minority, one class per grade will be selected to participate in the survey.
In order to achieve sufficient sample size to meet precision requirements for racial/ethnic-specific prevalence estimates, classes are double sampled within these high minority schools.
Two classes per grade instead of one will be selected in high minority schools that have sufficient enrollment to support a sample of 56 students in a given grade.
The method of selecting classes will vary from school to school, depending upon the organization of that school and whether schools are linked. The key element of the class sampling strategy is to identify a structure that partitions the students into mutually exclusive, collectively exhaustive groupings that are of approximately equal sizes. Beyond that basic requirement, we will do the partitioning to result in groups in which both sexes and all students have a chance to be selected. In selecting classes, we will generally give preference to selecting from mandatory courses such as English. Another option is to select from all classes that meet during a particular time of day such as all second or third period classes.
We will not use special procedures to sample for minorities at the school building level for two reasons:
Schools do not maintain student rosters that identify students by racial/ethnic affiliation.
Identifying student respondents based on race/ethnicity may be perceived as offensive by students and/or school administrators.
Selection of students
All students in a selected classroom will be eligible for the survey with the exception of students who cannot complete the survey independently (e.g., for language or cognitive reasons.)
Replacement of schools/school systems
We will not replace refusing school districts, schools, classes or students. We have allowed for school and student response in the sampling design. The numbers of selections are inflated to account for expected levels of non-response as discussed earlier.
Weighting and Variance Estimation
This section describes the procedures used to weight the data. From a sampling perspective, these include:
Sampling Weights
Nonresponse Adjustments and Weight Trimming
Post-stratification to National Estimates of Racial Percentages and Student Enrollment by Grade
Estimators and Variance Estimators
Although the sample was designed to be self-weighting under certain idealized conditions, it will be necessary to compute weights to produce unbiased estimates. The basic weights, or sampling weights, will be computed on a case by case basis as the reciprocal of the probability of selection of that case. Below is a simple presentation of the basic steps in weighting including sampling weight computation, nonresponse adjustments, and post-stratification adjustments.
Sampling Weights
If k is the number of PSUs to be selected from a stratum, Ni is the size of stratum i and Nij is the size of PSU j in stratum i (in all cases "size" refers to student enrollment), then the probability of selection of PSU j is k×Nij/Ni.
Assuming three large schools are to be selected in stratum i, Nijk is the size of school k in PSU j in stratum i, then the conditional probability of selection of the school given the selection of the PSU is 3×Nijk/Nij for YRBS Large schools.
The derivation is similar for small schools, with an extra factor to account for PSU subsampling probability.
If Cijk is the number of classes in school ijk then the conditional probability of selection of a class is just 1/Cijk (or 2/Cijk if two classes are taken). Since all students are selected, the conditional probability of selection of a student given the selection of the class is unity.
The overall probability of selection of a student in stratum is the product of the conditional probabilities of selection. The probabilities of selection will be the same for all students in a given school, regardless of their ethnicity.
Sampling weights assigned to each student record are the reciprocal of the overall probabilities of selection for each student.
Non-response Adjustments, Raking and Trimming
Several adjustments are planned to account for student and school nonresponse patterns. An adjustment for student nonresponse will be made by sex and grade within school. With this adjustment, the sum of the student weights over participating students within a school matches the total enrollment by grade and sex in the school collected during data collection. This adjustment factor will be capped in extreme situations, such as when only one or two students respond in a school, to limit the potential effects of extreme weights on the precision of survey estimates.
The weights of students in participating schools will be adjusted to account for nonparticipation by other schools. The adjustment uses the ratio of the weighted sum of measures of size over all selected schools in the stratum (numerator of adjustment factor), and over sum of the weighted measure of size for participating schools in a stratum (denominator of adjustment factor). The adjustment factor will be computed and applied to small and large schools separately.
For large schools the partial school weight is the inverse of the probability of selection of the school given that the PSU was selected:
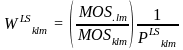
For small schools the partial school weight is:
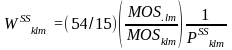
Extreme variation in sampling weights can inflate sampling variances, and offset the precision gained from a well-designed sampling plan. One strategy to compensate for these potential effects is to trim extreme weights and distribute the trimmed weight among the untrimmed weights. We will integrate the trimming and raking iterative processes as initiated during the 2015 YRBS in a way that makes both processes more efficient statistically as well as logistically.
Post-stratification approaches capitalize on known population totals and percentages available for groups of schools and students. National estimates of racial/ethnic counts for post-stratification are obtained from two sources described next. Private schools enrollments by grade and five racial/ethnic groups are obtained from the Private School Universe Survey (PSS). Public school enrollments by grade, sex, and five racial/ethnic categories are obtained from the Common Core of Data (CCD), both produced by the National Center for Education Statistics (NCES). These databases are combined to produce the enrollments for all schools, and to develop population counts to use as controls in the post-stratification step.
An iterative approach to post-stratification, called raking, will allow the use of additional post-stratification dimensions.
For post-stratification purposes, a unique race/ethnicity is assigned to respondents with missing data on race/ethnicity, those with an “Other” classification, and those reporting multiple races. For private schools, we use two race/ethnic classifications – white and non-white. For public schools we use the full five categories.
Estimators and Variance Estimation
If wi is the weight of case i (the inverse of the probability of selection adjusted for nonresponse and post-stratification adjustments) and xi is a characteristic of case i (e.g., xi=1 if student i smokes, but is zero otherwise), then the mean of characteristic x will be (Σ wixi)/(Σ wi). A population total would be computed similarly as (Σ wixi). The weighted population estimates will be computed with the Statistical Analysis System (SAS).
These estimates will be accompanied by measures of sampling variability, or sampling error, such as variances and standard errors, that account for the complex sampling design. These measures will support the construction of confidence intervals and other statistical inference such as statistical testing (e.g., subgroup comparisons or trends over successive YRBS cycles). Sampling variances will be estimated using the method of general linearized estimators8 as implemented in SAS survey procedures. These software packages must be used since they permit estimation of sampling variances for multistage stratified sampling designs, and account for unequal weighting, and for sample clustering and stratification.
1 Based on historical averages for the YRBS.
2 The design effect is defined as the ratio of actual variances attained under the actual design and the variances that would be obtained with a simple random sample of the same size.
3 Dalenius, T. and Hodges, K. (1959) “Minimum variance stratification.” Jour. Amer. Statist. Assoc., 54, 88-101.
4 The new method for frame construction improves coverage by using a frame that combines MDR and NCES data files rather than relying on a single source. This method adds a disproportionately large number of very small schools that used to be left out of the frames based solely on the MDR files.
5 In theory, bias due to loss of coverage of these very small schools might also be assessed by comparing selected estimates of risk behavior outcomes for students in these schools with estimates from the balance of the schools or with overall estimates. This comparison is not statistically possible, however, as the number of tiny schools is relatively small in recent cycles of the surveys, and so is the student yield in these schools.
6Errecart, M.T., Issues in Sampling African-Americans and Hispanics in School-Based Surveys. Centers for Disease Control, October 5, 1990.
7 The variance estimation process is more efficient without the need to account for certainty PSUs. The method of dividing large PSUs ensures that each sub-county PSU mirrors the distribution of schools in the county as a whole.
8Skinner CJ, Holt D, and Smith TMF, Analysis of Complex Surveys, John Wiley & Sons, New York, 1989, pp. 50.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Sophia.L.Stringfello |
| File Modified | 0000-00-00 |
| File Created | 2021-01-14 |
© 2025 OMB.report | Privacy Policy