L. Sampling an Weight Plan

The objective of the NYTS sampling design is to support estimation of tobacco-related knowledge, attitudes, and behaviors in a national population of public and private school students enrolled in grades 6 through 12 in the United States. More specifically, the study is designed to produce national estimates at a 95% confidence level by school level (middle school and high school), by grade (6, 7, 8, 9, 10, 11, and 12), by gender, and by race/ethnicity (non-Hispanic white, non-Hispanic black, and Hispanic). Additional estimates are also supported for subgroups defined by grade, by sex, and by race/ethnicity, each within school level domains; however, precision levels will vary considerably according to differences in subpopulation sizes.

The universe for the study consists of all public and private school students enrolled in regular middle schools and high schools in grades 6 through 12 in the 50 states and the District of Columbia. Alternative schools, special education schools, Department of Defense-operated schools, and vocational schools that serve only pull-out populations are excluded. Students enrolled in regular schools unable to complete the questionnaire without special assistance are also excluded.

The 2017 NYTS study is a continuation of the survey cycles that took place in 1999, 2000, 2002, 2004, 2006, 2009, and annually from 2011-2016. The NYTS employs a repeat cross-sectional design to develop national estimates of tobacco use behaviors and exposure to pro- and anti-tobacco influences. The 2011, 2013, and 2015 survey cycles of the NYTS were coordinated with the national Youth Risk Behavior Survey (YRBS); the 2017 NYTS is also intended to be coordinated with the 2017 YRBS.

Chapter 2 provides a description of the sampling design planned for the 2017 NYTS. Chapter 3 provides a description of the sampling methods. Chapter 4 describes the weighting plan.

Chapter 2—NYTS Sampling Design

2.1 Design Features for Minority Student Oversampling

To facilitate accurate prevalence estimates among racial/ethnic minority groups, prior cycles of the NYTS have employed multiple strategies to increase the number of non-Hispanic black and Hispanic students included in the sample. These have included over-sampling PSUs in high-minority strata, the use of a weighted measure of size (MOS), and double class selection in large schools that contain a sufficient proportion of minority students. This section provides an overview of these three approaches to oversampling minority students. Target sample sizes are further discussed in Sections 2.4 and 2.6 with details provided in Exhibit 2-1 and Exhibit 2-5.

Prior to the 2011 cycle of the NYTS, allocations oversampled strata with higher concentrations of non-Hispanic black and Hispanic students and led to precision losses overall. Starting with the 2011 NYTS, the design moved to a nearly proportional allocation of PSUs to first-stage sampling strata. As discussed in Section 2.5.1, the 2017 NYTS will adopt a nearly proportional allocation with slight oversampling of strata with higher concentrations of non-Hispanic black students. The reduction in oversampling areas of high minority concentrations represents the culmination of a trend in the design over the past several cycles, driven by changes in the underlying student population; in particular, a reduced need for oversampling PSUs in high Hispanic strata.

A weighted measure of size (MOS) was used in all NYTS cycles prior to 2013 to increase the probability of selection of high-minority PSUs and schools within a probability proportional to size (PPS) sampling design. As the use of an unweighted MOS increases the statistical efficiency of the design, the 2013 NYTS moved to the use of an unweighted MOS. That is, student enrollment was the measure of size used for the 2013-2016 NYTS cycles, and it will again be used in the 2017 NYTS.

In previous NYTS cycles, high-minority schools were subject to double class selection, such that two classes per grade were selected in these schools (compared to one class per grade in other schools) to increase the number of minority students sampled. The 2017 NYTS will continue this practice, with double class selection occurring in the subset of schools with largest concentrations of non-Hispanic black students. Our simulation studies conducted prior to sample selection will help finalize design parameters such as the class doubling thresholds.

2.2 Frame construction

Following the same approach in use since the 2014 NYTS, the 2017 NYTS sampling frame construction will use a combination of sources to create the school frame in order to increase school coverage. Along with the commercial Market Data Retrieval Inc. (MDR) dataset, we will use two files from the National Center for Education Statistics (NCES); the Common Core Dataset (CCD) which is a national file of public schools and the Private School Survey Dataset (PSS), a file of national non-public schools.

The reason for moving to a frame built from multiple data sources is to increase the coverage of schools nationally. As noted above, this dual-source frame build method was implemented for the first time for the 2014 NYTS after considerable testing and simulations¹. Including schools sourced from the two NCES files resulted in substantial coverage increases among all public and non-public middle and high schools.

For public schools, 84.6% of the resulting 103,596 schools were common across both files, with the NCES/CCD file supplying 9,732 (9.4%) unique schools, and the MDR file supplying 6,260 (6.0%) unique schools. For private schools, 54% of the 29,303 schools were common across both files, with the NCES/PSS file supplying 8,094 (27.6%) unique schools and the MDR file supplying 5,389 (18.4%) unique schools. Finally, after filtering the file for schools that contained students in grades 6 – 12, the frame contained 86,180 schools. Approximately 73% of these were common across both MDR and NCES sources, with the MDR file contributing 3,936 (9.1%) unique schools, and both NCES files contributing 12,595 (14.6%) unique schools.

Most of the added schools were smaller schools. The findings clearly demonstrated the gains in using multiple data sources, and has argued for the same approach in subsequent cycles.

2.3 Design Updates and Modifications

We plan to replicate the main features of the 2015 NYTS sample design conducted in coordination with the YRBS. As in the past few cycles, we will continue to adjust sampling parameters to reflect changing demographics of the in-school population.

2.3.1 Decreasing Need to Oversample Hispanic and Black Students

In general, as the proportion of black and Hispanic students in the study population increases and the minority population becomes more evenly distributed, the parameters that drive minority oversampling can be relaxed, allowing us to maintain yields while moving towards a statistically more efficient design.

Specifically, growing percentages of black and Hispanic students have allowed the design to adjust two dimensions towards greater design efficiency (i.e., closer to a self-weighting design):

The measure of size (MOS) will be eligible enrollment rather than a weighted MOS designed to oversample minority students;
The allocation to strata will be nearly proportional rather than oversampling strata with higher concentrations of minority students.

The historical data on the concentrations of black and Hispanic students reinforce the finding that oversampling via the measure of size is no longer necessary to achieve sufficient numbers of black and Hispanic students. Exhibits 2-1 and 2-2 present the percentages of public middle-school and high-school students who are black and Hispanic, respectively, for the years spanning the 2008 to 2015 period. These numbers were computed using the school sampling frames for each survey cycle.

Exhibit 2-1. Historical Trends for Inclusion of Non-Hispanic Black Students

Year	Percent
2008-09	16.67%
2010-11	16.17%
2012	15.96%
2013	16.83%
2014	16.83%
2015	15.27%

Exhibit 2-2. Historical Trends for Inclusion of Hispanic Students

Year	Percent
2008-09	20.70%
2010-11	21.80%
2012	22.46%
2013	22.72%
2014	22.72%
2015	23.20%

The tables show that while the percentage of non-Hispanic black students has slightly and gradually declined, the percentage of Hispanic students has been steadily increasing over the last few years. The percentage of Hispanic high-school students has increased from 20.7% in 2008 to 23.2% in 2015. (Note that the 2014 NYTS used the same school sampling frame as the 2013 NYTS.) Therefore, the double class sampling is now focused on schools with high concentrations of non-Hispanic black students. Along the same lines, the allocation will deviate from strict proportionality to slightly oversample strata with higher concentrations of non-Hispanic black students.

2.3.2 Design Updates

Other design features are routinely updated in each cycle such as:

The PSU definitions are adjusted to account for school openings and closings
The PSU sample sizes may be slightly adjusted—e.g., by one or two schools-- if the simulated yields indicate the need for adjusting sample sizes
The stratum boundaries based on the percentage of minority students are re-computed to minimize variances according to the cumulative square root rule (Dalenius-Hodges rule).^²
The allocation to strata is adjusted to remain nearly proportional while oversampling target strata; in this iteration, strata with higher concentrations of non-Hispanic black students
The cutoffs for double class sampling are fine tuned to meet target sample sizes in key analytic subgroups (minority student groupings by grade level) and overall

2.3.3. School Size Threshold

In past cycles of the NYTS, we have imposed a school size threshold so that the frame would not include very small schools, defined as those with aggregate school enrollment of 25 or fewer students in the eligible grades (6-12). Based on simulation studies conducted with the current frame, we plan to modify this threshold for the 2017 NYTS to remove schools with aggregate school enrollment of 40 or fewer students in the eligible grades. The school size threshold was established primarily for cost efficiency, but also due to concerns about confidentiality, in consultation with CDC. The gains in efficiency may come at the price of under-coverage of small schools, with the potential for associated biases. However, we considered that the cost of recruiting and collecting data from very small schools outweighed the benefit of adding a relatively small number of students that attend this subset of schools (less than 1% of all eligible students). Furthermore, excluding these very small schools will lead to substantial efficiencies in recruitment efforts and in increased student yields per visited school.

2.4 Sampling Stages and Measure of Size

The three-stage cluster sample will be stratified by racial/ethnic composition and urban versus non-urban status at the first (primary) stage. PSUs are defined as a county, a portion of a county, or a group of counties. PSUs are classified as “urban” if they are in one of the 54 largest metropolitan statistical areas (MSAs) in the U.S using current American Community Survey (ACS) data from the US Census Bureau. Otherwise, they are classified as “non-urban.” Additional, implicit stratification will be imposed by geography by sorting the PSU frame by state and by 5-digit ZIP Code. Within each stratum, a PSU will be randomly sampled without replacement at the first stage. In subsequent sampling stages, a probabilistic selection of schools and students will be made from the sampled PSUs.

The sampling stages may be summarized as follows:

Selection of PSUs—Eighty- five PSUs will be selected from sixteen strata (see section 2.5.1 below) with probability proportional to the total number of eligible students enrolled in all eligible schools located within a PSU.
Selection of Schools—At the second sampling stage, a total of 170 large schools or second-stage units (SSUs) will be selected from the 85 sample PSUs. An additional 20 medium SSUs and 30 small SSUS will be selected from subsampled PSUs, for a total of 220 sample SSUs (220=170+20+30). The PSU subsamples will be selected with simple random sampling, and the schools will be drawn with probability proportional to the total number of eligible students enrolled in a school.
Selection of Students—Students will be selected via whole classes whereby all students enrolled in any one selected class will be chosen for participation. Classes will be selected from course schedules provided by each school that agrees to participate. Schedules will be constructed such that all eligible students have only a single chance of selection.

Schools will be stratified into small, medium, and large schools based on their ability to support less than one, one, or two class selection per grade. Operationally, small SSUs contain fewer than 28 students at any grade level, medium SSUs contain between 28 and 55 per grade, and large SSUs contain at least 56 students at each grade level. We will select two classes per grade in selected large schools, and one class per grade in the remaining schools. The threshold for double class sampling will be set based on the simulation study. This will ensure that the required numbers of minority students are achieved per school level.

The sampling approach utilizes PPS sampling methods with the MOS defined as the count of final-stage sampling units, students. Coupled with the selection of a fixed number of units, the design results in an equal probability of selection for all members of the universe (i.e. a self-weighting sample). For the NYTS, we approximate these conditions, and thus obtain a roughly self-weighting sample.

The MOS will be used also to compute stratum sizes and PSU sizes. Assigning an aggregate measure of size to PSU, the sample allocates the PSU sample in proportion to the student population. Exhibit 2-3 presents a high level summary of the key sampling design features that will be described in the next section.

Exhibit 2-3: Key Sampling Design Features

Sampling Stage	Sampling Units	Stratification	Measure of Size	Designed Sample Size
1	PSUs: Counties, portions of a county, or groups of counties	Urban vs. Non-urban (2 strata); Minority concentration (8 strata)	Aggregate school size in target grades	85 Counties, portions of a county, or groups of counties
2	Schools	Small, medium and large; High-school vs. middle-school	Aggregate eligible enrollment	220 SSUs (school) selections: 170 large schools (2 per PSU), 20 medium schools and 30 small schools
3	Classes/ students			2 classes per grade in large high-minority schools; 1 class per grade otherwise

2.5 Stratification and Linking

This section describes the steps that are necessary for the selection of the first- and second-stage samples of PSUs and schools, organizing counties into PSUs, linking schools into SSUs, and the stratification and allocation methods at each of these stages.

2.5.1. Primary Sampling Units

Defining a PSU

In general, PSUs are geographic areas defined as counties or groupings of counties. In defining a PSU, several issues are considered:

In defining PSUs, several issues are considered:

Each PSU should contain at least 4 middle and 5 high schools.
Each PSU should be large enough to contain the requisite numbers of schools and yet not so large as to be selected with near-certainty.
Each PSU should be compact geographically so that field staff can go from school to school easily.
Recent data should be available to characterize each PSU.

Generally, counties were equivalent to PSUs with two exceptions:

Low population counties are combined to provide sufficient numbers of schools and students; and
Counties that are very large may be split to avoid becoming near-certainty PSUs.

Certainty PSUs are those whose size is large enough to ensure selection with probability one (1.0) with a PPS sampling design that selects larger PSUs with larger probabilities. As certainty PSUs lead to inefficiencies in the design, they are split so that the new smaller units are no longer selected with a probability of one. Near-certainty units (those with probability of selection of greater than 0.9) are also split to build in a safety buffer in the PSU sizes. County population figures will be aggregated from school enrollment data for the grades of interest.

The 2017 NYTS PSU definitions will be based on the definitions developed for the coordinated 2015 YRBS/NYTS cycle, and also used on the 2016 NYTS cycle. The exact PSUs defined in 2017 NYTS sampling frame will be updated to ensure that all PSUs meet the criteria above.

Stratification of PSUs

The PSUs are organized into 16 strata, based on urban/non-urban location (as defined below) and racial/ethnic minority enrollment of non-Hispanic blacks and Hispanics. In the traditional stratification used by the NYTS the classification of PSUs into the two racial/ethnic minority strata is based on the predominant minority in the PSU. This classification is coupled with the density distribution of non-Hispanic blacks and Hispanics to subdivide each of the four primary strata into four substrata, indexed by 1-4 according to this density. The approach involves the computation of optimum stratum boundaries using the cumulative square root of “f” method developed by Dalenius and Hodges³. The boundaries or cutoffs change as the frequency distribution (“f”) for the racial groupings change from one survey cycle to the next. These rules are summarized below.

If the PSU is within one of the 54 largest MSA in the U.S. it is classified as “urban,” otherwise it is classified as “nonurban.”
If the percentage of Hispanic students in the PSU exceeded the percentage of non-Hispanic black students, then the PSU is classified as Hispanic. Otherwise it is classified as non-Hispanic black.
Hispanic urban and Hispanic nonurban PSUs were classified into four density groupings, depending upon the percentages of Hispanics in the PSU.
Non-Hispanic Black urban and non-Hispanic black nonurban PSUs also were classified into four groupings, depending upon the percentages of non-Hispanic blacks in the PSU.

Allocation of the PSU Sample

We will select a sample of 85 PSUs to balance the objectives of maximizing the precision of overall estimates and ensuring the precision for minority student subgroup estimates. The first objective is achieved by a proportional allocation (i.e. an allocation of PSUs in proportion to student enrollment). The second objective is met by deviating from proportional allocation to assign a larger sample size to strata with higher concentrations of non-Hispanic black and/or Hispanic students. As the non-Hispanic black student yields have been declining and falling slightly short of target sample sizes in the last couple of cycles of the NYTS, we will make adjustments to the initial allocation to ensure that racial/ethnic minority targets would be met.

Exhibit 2-4 shows the planned allocation which, compared to that used for the 2015 and 2016 studies, shifts many of the PSUs to the strata with higher concentrations of non-Hispanic black students.

Specifically, the adjustments will increase the allocation to the high-black strata in the way described in Exhibit 2-4. Note that the total student enrollment is 11,900,917 aggregated over the eight majority non-Hispanic black strata and 17,155,991 aggregated over the eight majority Hispanic strata, so the latter strata still get assigned more sample PSUs so that the allocation does not deviate much from a proportional allocation.

Exhibit 2-4: Preliminary Stratum Definition and PSU Allocation to Strata

Predominant Minority	Urban/Rural	Density Group Number	Stratum Code	Student Population	Number of Sample PSUs (Revised)
Non-Hispanic Black	Urban	1	BU1	2,720,181	7
		2	BU2	975,490	4
		3	BU3	908,299	4
		4	BU4	516,712	5
	Nonurban	1	BR1	3,937,157	8
		2	BR2	1,503,403	4
		3	BR3	1,026,612	4
		4	BR4	313,063	5
Hispanic	Urban	1	HU1	3,530,556	8
		2	HU2	2,429,442	7
		3	HU3	1,865,988	5
		4	HU4	2,106,242	4
	Nonurban	1	HR1	4,427,215	12
		2	HR2	1,284,402	3
		3	HR3	988,655	3
		4	HR4	523,491	2

2.5.2. Schools

Shape1

Exhibit 2-3: Linked School Construction and Grade Sampling for High Schools

Linking into Second-stage Sampling Unit

High schools are classified as “whole” if they have grades 9 through 12; middle schools are “whole” if they have all grades 6–8. Otherwise, they are considered a “fragment” school. Fragment schools form component schools that are linked with other schools (fragment or whole) to form a linked school that has all four grades. This process is illustrated in Exhibit 2-3, where Fragment School A is linked with Whole School B, to form a linked school, or SSU XXX. We link schools before sampling using an algorithm, developed for use in the national YRBS. The algorithm links geographically proximate schools. Linked schools are treated as a single school sampling unit during sampling with selection performed at the grade level as described below.

Stratification

SSUs are stratified by school level (middle and high) and by size. Middle schools are those that contain any of grades 6 through 8, and high schools are those that contain grades any of grades 9 through 12. Schools that contain a mix of high- and middle-school grades are split into two sampling units, one for each school level. Operationally school size is defined as SSUs with the following enrollment by grade:

Large SSU = a minimum of 56 students in every grade
Medium SSU = a minimum 28 to 55 students in every grade
Small = fewer than 28 students in at least one grade

Therefore, to be defined as a small school, only one grade need fall below the threshold of fewer than 28 students.

2.6 Sample Sizes

The original specifications for NYTS sample sizes were not given in terms of student yields; rather, they were specified in terms of the precision of the resulting estimates. The required student yields, or numbers of participating students, will be translated into the necessary numbers of sample schools, and sample PSUs, using historical participation rates.

The NYTS is designed to produce accurate estimation to within ± 5% at a 95% precision level for the following key subgroup estimates:

Middle and high school (school level): middle school students in total (grades 6–8 combined) and high school students in total (grades 9–12 combined)
Grade: individual grades 6, 7, 8, 9, 10, 11, and 12
Sex: males and females in total, by school level (e.g., male middle school students, female high school students), and by individual grade (e.g., 6-grade males, 6-grade females)
Race/Ethnicity: in total and by school level (e.g., Hispanic middle school students)

The sample sizes will be developed to support analysis by individual grade and by sex without any special considerations in the sampling plan. Design effects are assumed by the design to be relatively small for subgroups that cut across schools; therefore, estimates by sex will have better precision than other subgroups. Thus, the designed confidence intervals will be ± 3%. Because the design is expected to yield a greater number of completed surveys from high school students than from middle school students, overall estimates are anticipated to be more precise at the high school level than those at the middle school level. Moreover, because within grade estimates by sex have slightly larger standard errors than those for estimates by grade alone, estimates by sex and by grade are expected within ± 5%.

The 2017 NYTS sampling design is aimed at balancing student yields by grade unlike the 2012 and 2014 sample designs which aimed at balance by school level (middle and high school). Previous designs aimed at balance by school level had targets of 10,000 students per level. For the 2017 NYTS, the target sample sizes correspond to approximately 2,800 participating students per grade so that they also ensure the precision of estimates by individual grade (e.g., sex by grade subgroup estimates on the basis of about 1,400 students). These grade totals would correspond to a total of 8,400 middle schools students and 11,200 high school students.

Across the eleven previous cycles of the NYTS, the school participation has averaged 84.7%, with a low of 72.5%. Student participation has averaged 82.8% with a low of 87.4%. Historical participation rates at both school and student levels, which guide the sampling design and sample sizes, are summarized in Exhibit 2-5. The combined or overall response rate averages 76.2%.

In calculating the sample sizes for the 2017 NYTS, we conservatively assume a combined rate (student x school) of 72%.

The NYTS sample size calculations are premised on the following assumptions:

The main structure of the sampling design will be consistent with the design used to draw the sample for prior cycles of the NYTS.
The selection of a minimum of one SSU at the high school level and one SSU at the middle school level within each PSU. Some PSUs are selected to provide up to four extra schools (due to school linking and multiple sample hits for very large PSUs).
SSUs with at least 56 students per grade are considered large, and those among the others with at least 28 students per grade are considered medium; otherwise they are considered small.
On average, each selected class will include 28 students (on the basis of historical averages).
For SSUs classified as large schools and high minority (those with higher concentrations of non-Hispanic black students), we will sample double the amount of students by sampling eight classes instead of four.
A 72% overall response rate (based on historical averages) calculated as the product of the school and student response rate.

Exhibit 2-5: Historical Summary of NYTS Participation Rates

YEAR	School Participation	Student Participation	Overall
1999	90.3%	93.2%	84.2%
2000	90.0%	93.4%	84.1%
2002	83.1%	90.6%	75.3%
2004	92.7%	87.9%	81.5%
2006	91.6%	87.6%	80.2%
2009	92.3%	91.9%	84.8%
2011	83.2%	88.0%	73.2%
2012	80.3%	91.7%	73.6%
2013	75.4%	90.7%	68.4%
2014	80.2%	91.4%	73.3%
2015	72.5%	87.4%	63.4%
^{Average over all previous cycles}	84.7%	90.0%	76.2%

The NYTS sample size calculations are premised on the following assumptions:

The main structure of the sampling design will be consistent with the design used to draw the sample for prior cycles of the NYTS.
The selection of a minimum of one SSU at the high school level and one SSU at the middle school level within each PSU. Some PSUs are selected to provide up to four extra schools (due to school linking and multiple sample hits for very large PSUs).
SSUs with at least 56 students per grade are considered large, and those among the others with at least 28 students per grade are considered medium; otherwise they are considered small.
On average, each selected class will include 28 students (on the basis of historical averages).
For SSUs classified as large schools and high minority (those with higher concentrations of non-Hispanic black students), we will sample double the amount of students by sampling eight classes instead of four.
A 72% overall response rate (based on historical averages) calculated as the product of the school and student response rate.

Based on these assumptions, we will select a sample of 85 PSUs. Within each of the 85 sample PSUs, we will draw two large schools, one at the middle school level to supply students in grades 6 through 8, and one at the high school level to supply students in grades 9 through 12. In addition, 10 and 15 PSUs will be independently sub-sampled to supply medium and small SSUs at each level, respectively. The anticipated number of students selected from all sample schools will be 27,789 students (before non-response). The estimated number of participants is 20,008 assuming a combined response rate of 72%.

Exhibit 2-6 provides a detailed calculation of designed sample sizes across school level and school size categories.⁴

Exhibit 2-6: Planned Sample Sizes for the 2017 NYTS

PSU	Size	# of SSUs	Number of Schools Sampled	Number of Classes per School	Number of Students per Class	Number of Sampled Students prior to Attrition	Combined School and Student 72% Response Rate
85	Large HS	85	Double classes: 39	8	28	8,758	6,306
	Large HS	85	Single classes: 46	4	28	5,141	3,702
	Large MS	85	Double classes: 39	6	28	6,569	4,730
	Large MS	85	Single classes: 46	3	28	3,856	2,776
	Large Total	170				24,324	17,513

10 (sub-sample)	Medium HS	10	10	4	28	1,120	806
	Medium MS	10	10	3	28	840	605
	Medium Total	20				1,960	1,411

15 (sub-sample)	Small HS	15	15	3.8	18.1	1,030	742
	Small MS	15	15	2.8	11.2	475	342
	Small Total	30				1,505	1,084

	Overall Total	220				27,789*	20.008

*Note that this was the anticipated number of students in all sampled schools, and the actual number of sampled students is derived only from participating schools (and is thus considerably lower).

2.6.1. Middle School and High School Estimates

Estimates by school level are required to support separate analysis of students across middle school grades (6, 7, and 8) and high school grades (9, 10, 11, and 12). However, schools tend to vary in their grade structures, an inconsistency that compromises the ability to easily and efficiently link schools for sampling purposes in a manner that also uniformly divides students by grade. For example, 9^th grade students are served by both grades 7–9 junior high schools and by grades 9–12 high schools. As a result, we have developed the school linking approach described earlier in Section 2.5.2, with this approach being applied independently for high schools and middle schools.

2.6.2. Grade Estimates

The designed sample size is approximately balanced for school-level and for grade-level groupings. By targeting at least 2,800 students per grade, the sample ensures that estimates at the grade level achieve the required precision levels.

2.6.3. Sex Group Estimates

The large designed sample size permits analysis by sex without any special considerations in the sampling plan. During the class selection process, frames of eligible classes from co-educational schools in which classrooms were segregated by gender (i.e., an all-male or all-female class) are avoided if at all possible.

2.6.4. Race/Ethnicity Group Estimates

In order to support separate analysis of the data for non-Hispanic white, non-Hispanic black and Hispanic students, in total and by school level, adequate sample sizes are required by the designed for subgroups defined by: 1) school level by racial grouping; or 2) by sex grouping. Sample sizes are not designed, however, to support detailed analyses by sex and school level within racial/ethnic subgroups (e.g., middle school Hispanic males).

Chapter 3— Sampling Methods

This chapter describes the methods traditionally used by the NYTS in the selection of PSUs, schools, grades, and classes of students. In this process, we define the probabilities of selection associated with the various sampling stages as follows:

Probability of selecting PSUs
Probability of selecting schools
Probability of selection of grades
Probability of selecting classes and students

These probabilities provide the basis for the sampling weights discussed in Chapter 4.

The overall probability of selection for a student is the product of the probability of selection of the PSU, which is a group of schools, multiplied by the conditional probability of selecting the student's school, multiplied by the conditional probability of selecting the student's class. These steps are detailed in the selection below.

3.1 Primary Sampling Unit

Selection

Within each first-stage stratum, the PSUs will be sorted by five-digit ZIP Code to attain a form of implicit geographic stratification. Implicit stratification, coupled with the probability proportional to size (PPS) sampling method described below, ensures geographic sample representation. With PPS sampling, the selection probability for each PSU is proportional to the PSU’s measure of size.

The following systematic sampling procedures are applied to the stratified frame to select a PPS sample of PSUs.

Select 85 PSUs with a systematic random sampling method within each stratum. The method applies within each stratum a sampling interval computed as the sum of the measures of size for the PSUs in the stratum divided by the number of PSUs to be selected in the stratum.
Subsample at random 10 of the sample PSUs for the medium school sample for each school level (middle school and high school)
Subsample at random 15 of the sample PSUs for the small school sample for each school level (middle school and high school)

Probability

If MOS_klm is the measure of size for school k in PSU l in stratum m and if K_m is the number of PSUs to be selected in stratum m, then P^p_lm is the probability of selection of PSU l in stratum m:

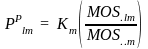
For the PSUs subsampled for the selection of medium and small schools, the sub-sample PSUs have an additional factor in their selection probability for these schools. This factor is incorporated into the school sampling probability below, as it is more closely associated with school selection.

3.2 School Selection

Selection

For large schools, one high school and one middle school are selected with PPS systematic sampling within a PSU. The schools are selected into the sample with probability proportional to the measure of size.

Small and medium schools will be sampled independently from large schools; they will be set in two separate strata sampled at lower rates. This approach will be implemented by drawing a sub-sample of 15 PSUs for the sampling of small schools and a subsample of 10 PSUs for medium school sampling at each school level. Then one small school or medium school will be selected in each sub-sampled PSU with probability proportional to the measure of size.

Replacement of Schools/School Systems

We will not replace refusing school districts, schools, classes, or students; we will, however, replace schools found to be ineligible during the recruitment process. We allow for school and student non-response by inflating the sample sizes to account for non-response. With this approach, all schools can be contacted in a coordinated recruitment effort, which is not possible for methods that allow for replacing schools.

Probability

The probability of selecting large school k in PSU l and stratum m, P^LS_klm, at each level is computed as follows:

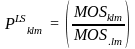
For medium schools, one school is drawn from sub-sampled PSU, so the probability of selection of a medium school at each level, P^MS_klm, then becomes:

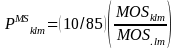
For small schools, one school is drawn from sub-sampled PSU at each level, so the probability of selection of a small school, P^SS_klm, then becomes:

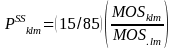
Note the additional sampling factor in the probability of selection for small schools and medium schools is due to the PSU sub-sampling for these schools as noted above.

3.3 Grades

Selection

Except for linked schools, all eligible grades are included in the class selection for each school.

In linked schools, grades are selected independently. One component school is selected to provide classes at each grade level, and grades within component schools are drawn with probability proportional to grade enrollment.

Probability

Most SSUs in the sample contained one component school. In these cases, all eligible grades are selected so that the probability of selecting a grade is 1.0.

In SSUs that are made up of more than one component schools, the selection of the component school at each grade is made with PPS sampling. The school selections from the component school at each grade level are made independently.

We denote this P^G_jklm the probability of selecting grade j in SSU k, in PSU l, stratum m. For the j^th grade within SSU k, this probability is equal to the ratio of the number of students at grade j in the component school to the total enrollment in grade j across all component schools within the SSU

3.4 Classes

Selection

In large schools, we select an average of 1.46 classes per grade by selecting 2 classes per grade in 46% of the selected large schools and one class per grade in the remaining schools. The double class sampling will take place in schools with higher concentrations of non-Hispanic black students and one class per grade in the remaining schools.

One class per grade is selected in medium schools. In small schools, that is, those that could not support a full class selection at each grade, all students in all eligible grades are taken into the sample.

All students in a selected class who can complete the survey without special assistance are considered eligible and offered the opportunity to participate in the survey. Refusing students are not replaced. Non-response at the student level is accounted for in the sample size using an average per class yield that assumes student response rates derived from historical experience with the NYTS.

A set of classes is identified for each school at each grade level such that every student in a given grade level is enrolled in exactly one of the classes in the set. For example, a required English course might be used. Selections are made at all eligible grade levels in the school.

Probability

The probability of selection of a class when there are C_jklm classes at grade j in school k, PSU_i, stratum m is just 1/C_jklm or 2/C_jklm depending on whether 1 or 2 classes are taken in the school. All students in a selected class were chosen so the probability of selection of a student is the same as the class (i.e., 1/C_jklm or 2/C_jklm).

Note that the probability of student selection within a class does not vary by race, ethnicity or gender. We denote this probability as P^C_ijklm as the probability of selecting class i in grade j, school k, PSU l, stratum m. Since every student in a selected class is also selected, the probability of selecting any student in class i, grade j, school k, PSU l, stratum k, is also equal to P^C_ijklm.

Chapter 4—Weighting

4.1 Overview

This chapter describes the procedures planned for weighting the NYTS 2017 data. The process will involve the steps outlined below:

Sampling weights
Non-response adjustments
Post-stratification and weight trimming

The final student level response data are weighted to reflect the initial probabilities of selection and non-response patterns, to mitigate large variations in sampling weights, and to post-stratify the data to known sampling frame characteristics.

4.2 Sampling Weights

The sampling weight attached to each student response is the inverse of the probability of selection for that student. This basic weight can be adjusted to compensate for non-response to alleviate excess weight variation and to match the weighted data to known control totals. A convenient way of computing the basic weight is by inverting the probabilities of selection at each stage to derive a partial weight or stage weight. The stage weights are then multiplied together to form the overall weight.

4.2.1 Adjusted Conditional Student Weights

The adjusted conditional student weight is the student weight given the selection of the PSU, school and grade. This weight is the product of the inverse of the probability of selection, a non-response adjustment and a ratio adjustment to control to known school enrollment totals. This three step process is simplified to the ratio of the number of enrolled students to the number of responding students in a given weighting class within a school.

We denote the student selection weight W^R_cklm, where the subscripts k, l, and m refer to the school, PSU and stratum as before. The subscript c refers to the weight computation class, described below. This weight is computed as below, where N is the number of enrolled students⁵ and R is the number of responding students in weighting class c within a given school:

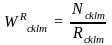
The weighting class definition is set dynamically, as described next, so as to avoid extreme weights.

Weighting class c is defined by a sequence of rules that depends on the number of responding students. This is done to avoid large weights for classes with low numbers of respondents. This process operates entirely within school.

Initially the weighting class is defined by grade and gender within each school. We then combine weighting classes if the weight for the class exceeds a maximum value. This cap C is computed using the equation following.

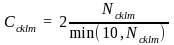
The combination sequence first combines males and females within grade. Then both the cap and the weight are re-computed. If the weight still exceeds the cap, grades are combined. The process is repeated, and if the student weight still exceeds the cap, the school is taken as the weight class.

This has the effect, within school, of setting an upper limit on the weight in class C of 2 in weight classes with an enrollment of less than 10, and 20% of the enrollment in weight classes with an enrollment of more than 10⁶.

4.2.2 School Sampling Weights

For large schools the partial school weight is the inverse of the probability of selection of the school given that the PSU was selected:

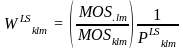
For medium schools the partial school weight is:

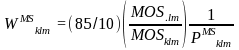
For small schools the partial school weight is:

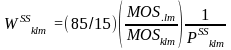
4.2.3 Grade Sampling Weights

The partial weight for a grade, given the selection of the linked school containing it, is simply the inverse of the probability of selection described in Chapter 2. In a non-linked school the weight is 1.0. We denote the grade weight as W^G_jklm.

4.2.4 PSU Sampling Weights

The weight of the PSU is the inverse of the probability of selection of that PSU:

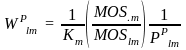
For small schools and medium school selections, the enclosing PSU were drawn as a subsample. This PSU subsampling component of the PSU weight is accounted for in the school selection probability and corresponding weight.

4.2.5 Overall Sampling Weight

The overall sampling weight is formed as the product of the stage selection weights. This weight, W^T1, is then adjusted for non-response, trimmed, and post-stratified to control totals as described in the following sections. This weight is computed as:

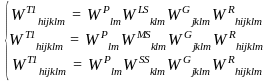
for large schools, medium schools, and small schools respectively, where the weights in the right hand side of the equations are defined in the preceding sections.

4.3 Non-Response Adjustments

This section describes how weights are adjusted for nonparticipation by entire schools, using strata as weighting classes. The adjustment process is different in small schools than in medium and large schools, as represented by the following equations for the adjustment factor.

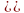
_{The
first equation applies to large and medium schools combined, and the
second applies to small schools. Note that this adjustment is made
within stratum for large and medium schools and across the whole
sample for small schools.}The student weight, adjusted for non-response, is A^SS_lm W^T1_hijklmfor small schools and A^LS_lm W^T1_hijklmfor large and medium schools.

4.4 Post-stratification and Weight Trimming

The final two steps in the weighting process include trimming and post-stratification. Trimming procedures are used to control the weight variability and reduce its impact on survey variances. Post-stratification methods ensure that weighted totals sum to population control totals and therefore, minimize the potential for biases due to non-response and non-coverage.

We will use the method developed and used in the 2015 NYTS, which is an iterative approach combining post-stratification and trimming.⁷^,⁸ The methods incorporate a model-based approach to variable selection in weight trimming while controlling for extreme variability in weights across sampling units. By combining the two iterative methods in one approach, the rake-trim method ensures that trimmed weights retain their variance-reducing feature after post-stratification. Conversely, it also ensures that post-stratified weights add up to control totals.

Similar to weighting, the raking and trimming methods will be conducted separately for middle schools and high schools. In each iteration of the raking method, post-stratification will be performed along two dimensions: a) school type (public or private)/ grade/ race-ethnicity, and b) school type/ grade/ gender. These two classes are defined so that control totals are known and cells have reasonable size. Public schools are raked to totals by grade and race-ethnicity while private schools are raked to grade totals. Within the same iteration, this step is followed by the trimming step which truncates (or “caps”) the weight using the overall weight distribution (i.e. percentiles). The trimming method uses the interquartile range (IQR) as the basis for a threshold for weights that are excessively large. Specifically, any weights that exceed the median weight plus 4 times the IQR are trimmed.3 The excess weight is then distributed among the observations within each cell to ensure that effective post-stratification totals are preserved.

To obtain accurate counts of students in schools considered eligible for the NYTS by grade, gender, and race for use in post-stratification, we will turn to data available in two NCES data files. Private schools enrollments by grade and five racial/ethnic groups will be obtained from the Private School Universe Survey (PSS), and public school enrollments by grade, gender, and five racial/ethnic categories will be obtained from the Common Core of Data (CCD). These databases will be combined to produce the enrollments for all schools, and to develop population percentages to use as controls in the post-stratification step.

Specifically, population control totals for public school enrollments will be taken from the most recent CCD Public Elementary/Secondary School Universe Survey. Control totals for private school enrollments will be taken from the most recent NCES PSS.

1 Redesigning National School Surveys: Coverage and Stratification Improvement using Multiple Datasets William Robb, Kate Flint, Alice Roberts, Ronaldo Iachan - ICF International, FEDCASIC March 2014

2 Dalenius, T. and Hodges, K. (1959) “Minimum variance stratification.” Jour. Amer. Statist. Assoc., 54, 88-101.

3 Dalenius, T., & Hodges, J. L. (1959). Minimum Variance Stratification. Journal of American Statistical Association, 54, 88−101.

Average over all previous cycles

4 In this exhibit, the schools are secondary sampling units (SSUs), or “virtual schools”, created by combining actual, physical schools so that each virtual school unit has a complete set of grades for the level. The virtual schools are expanded to physical schools.

5 The student enrollment for each school used in this calculation is obtained from the school during data collection. These counts are obtained by grade and gender.

6 The cap could be exceeded in cases where the weight class is collapsed to the school level.

7 Iachan R (2010, August). A new iterative method for weight trimming and raking. Paper presented at the American Statistical Association meeting. Vancouver. Canada

8 Izrael D, Battaglia MP, Frankel MR. (2009). Extreme survey weight adjustment as a component of sample balancing (a.k.a. Raking), Paper 274-2009, SAS Global Forum 2009.

File Type	application/vnd.openxmlformats-officedocument.wordprocessingml.document
Author	Windows User
File Modified	0000-00-00
File Created	2021-01-14

L. Sampling an Weight Plan

L_NYTS 2017_Sampling and Weighting Plan.docx

National Youth Tobacco Surveys (NYTS) 2020