NAEP 2024 Appendix B Weighting Procedures
NAEP 2024 Appendix B v30.docx
National Assessment of Educational Progress (NAEP) 2024 Amendment #2
NAEP 2024 Appendix B Weighting Procedures
OMB: 1850-0928
NATIONAL CENTER FOR EDUCATION STATISTICS NATIONAL ASSESSMENT OF EDUCATIONAL PROGRESS
National Assessment of Educational Progress (NAEP) 2024
Appendix B
NAEP 2018 Weighting Procedures
OMB# 1850-0928 v.30

June 2023
The 2018 Weighting Procedures documentation is the most current version available to the public. At this time, there is not a timeline for when the details for later assessment years will be publicly available.
NAEP Technical Documentation Website
NAEP Technical Documentation Weighting Procedures for the 2018 Assessment
NAEP assessments use complex sample designs to create student samples that generate population and subpopulation estimates with reasonably high precision. School and student sampling weights ensure valid inferences from the school and student samples to their respective populations. In 2018, weights were developed for schools and students sampled at grade 8 for assessments in civics, geography, U.S. history, and technology and engineering literacy (TEL).
Student Weights
The assessments for civics, geography, and U.S. history at grade 8 in both public and private schools were administered in two modes: paper and pencil mode, and a digital mode using tablets. As described in the NAEP 2018 sample design section, the random sample of students assigned to the paper-based assessment (PBA) group were assessed using paper and pencil, and the random sample of students assigned to the digitally based assessment (DBA) group were assessed using tablets. Separate sampling weights were computed for the DBA-only sample, PBA-only sample, and DBA and PBA samples combined. The weighting procedures for the civics, geography, and U.S. history assessments described in this report are
Computation of Full-Sample Student Weights
Computation of Replicate Student Weights for Variance Estimation
Computation of Full-Sample School Weights
Computation of Replicate School Weights for Variance Estimation
Quality Control on Weighting Procedures
based on combined DBA/PBA samples. The TEL assessment at grade 8 for public and private schools was only administered to students via tablets and therefore involved the computation of only one set of weights.
Each student was assigned a weight to be used for making inferences about students in the target population. This weight is known as the final full- sample student weight, and it contains six major components:
 the
student base
weight,
the
student base
weight,


 school
nonresponse adjustment, student
nonresponse adjustment, school
weight trimming
adjustment,
school
nonresponse adjustment, student
nonresponse adjustment, school
weight trimming
adjustment,

 student
weight trimming
adjustment, and
student raking
adjustment.
student
weight trimming
adjustment, and
student raking
adjustment.
The student base weight is the inverse of the overall probability of selecting a student and assigning that student to a particular assessment. The sample design that determines the base weights is discussed in the NAEP 2018 sample design section.
The student base weight is adjusted for two sources of nonparticipation: school level and student level. These weighting adjustments seek to reduce the potential for bias from such nonparticipation by
 increasing
the weights
of students
from schools
similar to
those schools
not participating,
and
increasing
the weights
of students
from schools
similar to
those schools
not participating,
and
 increasing
the weights
of participating
students similar
to those
students from
within participating
schools who
did not
attend the
assessment session
(or makeup
session) as
scheduled.
increasing
the weights
of participating
students similar
to those
students from
within participating
schools who
did not
attend the
assessment session
(or makeup
session) as
scheduled.
Furthermore, the final student weights reflect the trimming of extremely large weights at both the school and student levels. These weighting adjustments seek to reduce variances of survey estimates.
An additional weighting adjustment was implemented in the geography and U.S. history assessments so that estimates for key student-level characteristics were in agreement across those assessments. This adjustment was implemented using a raking procedure.
In addition to the final full-sample student weight, a set of replicate weights was provided for each student. These replicate weights are used to calculate the variances of survey estimates using the jackknife repeated replication method.
The methods used to derive these weights were aimed at reflecting the features of the sample design. When the jackknife variance estimation procedure is implemented, approximate unbiased estimates of sampling variance are obtained. In addition, the various weighting procedures were repeated on each set of replicate weights to appropriately reflect the impact of the weighting adjustments on the sampling variance of a survey estimate.
School Weights
In addition to student weights, school weights were calculated to provide secondary users means to analyze data at the school level. The school weights are subject specific and are computed for the schools that contained at least one student that participated in the NAEP assessment for that subject.
Each school was assigned a weight to be used for making inferences about schools in the target population. This weight, known as the final full-sample school weight, contains five major components:
 the
school base
weight,
the
school base
weight,



 school
nonresponse adjustment,
school weight trimming adjustment,
school-session assignment
weight, and
small-school subject
adjustment.
school
nonresponse adjustment,
school weight trimming adjustment,
school-session assignment
weight, and
small-school subject
adjustment.
The school base weight is the inverse of the overall probability of selecting a school for a particular assessment.
The school nonresponse adjustment increases the weights of participating schools to account for similar schools that did not participate, and the school trimming adjustment reduces extremely large weights to decrease variances of survey estimates. These two adjustments are the same school-level adjustments used in the final full-sample student weight described above.
The school-session assignment weight reflects the probability that the particular session type was assigned to the school.
The small-school subject adjustment accounts for very small schools that did not have enough participating students for every subject intended for the school. School weights for subjects that had at least one eligible student are inflated by this factor to compensate for schools of the same size that did not have any eligible students for those subjects and would not be represented otherwise.
In addition to the final full-sample weight, a set of replicate weights was provided for each school. These replicate weights are used to calculate the variances of school-level estimates using the jackknife repeated replication method.
 Quality
Control
Procedures
Quality
Control
Procedures
Quality control checks were implemented throughout the weighting process to ensure the accuracy of the full-sample and replicate school and student weights. See the Quality Control on Weighting Procedures link above for the various checks implemented and main findings of interest.

NAEP Technical Documentation Computation of Full-Sample School Weights for the 2018 Assessment
The full-sample or final school weight is the sampling weight used to derive NAEP school estimates of population and subpopulation characteristics for a specified grade (8) and assessment subject (civics, geography, U.S. history, or technology and engineering literacy (TEL)). The full-sample school weight reflects the number of schools that the sampled school represents in the population for purposes of estimation.
The full-sample weight, which is used to produce survey estimates, is distinct from a replicate weight that is used to estimate variances of survey estimates. The full-sample weight is assigned to participating schools and reflects the school base weight after the application of the various weighting adjustments. The full-sample weight SCH_WGTjs for school s in stratum j can be expressed as follows:
![]()
where

SCH_BWTjs is the school base weight;


 SCH_NRAFjs
is the
school-level nonresponse
adjustment factor;
SCH_TRIMjs
is the
school-level weight
trimming adjustment
factor; and
SCH_SUBJ_AFs
is the
small-school subject
adjustment factor.
SCH_NRAFjs
is the
school-level nonresponse
adjustment factor;
SCH_TRIMjs
is the
school-level weight
trimming adjustment
factor; and
SCH_SUBJ_AFs
is the
small-school subject
adjustment factor.
The small-school subject adjustment accounts for 1) very small schools that did not have enough participating students for every subject assigned to the school and 2) small schools assigned only one paper-based assessment (PBA) session type. School weights for subjects that had at least one eligible student are inflated by this factor to compensate for schools of the same size that did not have any eligible students for those subjects and would not be represented otherwise.
For the digitally based assessments (DBA), the factor is equal to the inverse of the probability that a school of a given size had at least one eligible sampled student in the given subject:
![]()
where


SF is the spiraling factor for the given subject and assessment mode; and
ns is the within-school student sample size.
For the 2018 operational assessments, schools could be assigned to four session types:
DBA civics/geography/U.S. history;
PBA geography/U.S. history;
PBA civics; or
DBA technology and engineering literacy (TEL).
Students in schools assigned to the DBA civics/geography/U.S. history sessions are assigned to subjects at rates of 7 in 23 for civics, 7 in 23 for geography, and 9 in 23 for U.S. history. These rates result in spiraling factors of 3.29, 3.29, and 2.56 respectively. If, for example, a school had only 1 (or 2) eligible students in civics, the small-school adjustment factor would be 3.29 (or 1.64). Students in schools assigned to the DBA TEL session had only one subject.
For PBA, the small-school subject adjustment factor formula includes an extra multiplier that reflects the probability that the particular PBA session containing the particular subject was assigned to the school. Students in schools assigned to the PBA geography/U.S. history sessions are assigned to subjects at rates of 4 in 9 for geography and 5 in 9 for U.S. history. Students in schools assigned to the PBA civics session had only one subject. The additional multipliers for the PBA civics and PBA geography/U.S. history session types were 9/4 and 9/5 respectively.
In summary, 46 of the 778 schools assigned to the civics assessment had their weights adjusted to compensate for schools that were too small to do civics. The small-school adjustment factors for civics ranged from 1.10 to 3.29. For the geography assessment, 44 of 777 schools had their school weights adjusted to compensate for schools that were too small to do geography. The small-school adjustment factors for geography ranged from 1.10 to
3.29. For the U.S. history assessment, 50 of 784 schools had their school weights adjusted to compensate for schools that were too small to do U.S. history. The small-school adjustment factors for U.S. history ranged from 1.28 to 2.56.

NAEP Technical Documentation Computation of Full-Sample Student Weights for the 2018 Assessment
The full-sample or final student weight is the sampling weight used to derive NAEP student estimates of population and subpopulation characteristics for a specified grade (8) and assessment subject (civics, geography, U.S. history, or technology and engineering literacy (TEL)). The full-sample student weight reflects the number of students that the sampled student represents in the population for purposes of estimation. The summation of the final student weights over a particular student group provides an estimate of the total number of students in that group within the population.
The full-sample weight, which is used to produce survey estimates, is distinct from a replicate weight that is used to estimate variances of survey estimates. The full-sample weight is assigned to participating students and reflects the student base weight after the application of the various weighting adjustments. The full-sample weight for student k from school s in stratum j (FSTUWGTjsk) can be expressed as follows:
![]()
where
Computation of Base Weights
School and Student Nonresponse Weight Adjustments
School and Student Weight Trimming Adjustments
Student Weight Raking Adjustment
 STU_BWTjsk
is
the
student
base
weight;
STU_BWTjsk
is
the
student
base
weight;




 SCH_NRAFjs
is the
school-level nonresponse
adjustment factor;
STU_NRAFjsk
is the
student-level nonresponse
adjustment factor;
SCH_TRIMjs
is the school-level weight trimming adjustment
factor; STU_TRIMjsk
is the
student-level weight
trimming adjustment
factor; and
STU_RAKEjsk
is the
student-level raking
adjustment factor.
SCH_NRAFjs
is the
school-level nonresponse
adjustment factor;
STU_NRAFjsk
is the
student-level nonresponse
adjustment factor;
SCH_TRIMjs
is the school-level weight trimming adjustment
factor; STU_TRIMjsk
is the
student-level weight
trimming adjustment
factor; and
STU_RAKEjsk
is the
student-level raking
adjustment factor.
School sampling strata for a given assessment vary by school type. See the links below for descriptions of the school strata for the various assessments.


 Public
school sample for social sciences
Private school
sample for
social sciences
Public school
sample for
TEL
Public
school sample for social sciences
Private school
sample for
social sciences
Public school
sample for
TEL
 Private
school sample
for TEL
Private
school sample
for TEL

NAEP Technical Documentation Computation of Base Weights for the 2018 Assessment
Every sampled school and student received a base weight equal to the reciprocal of its probability of selection. Computation of a school base weight varies by

 type
of sampled
school (original
or substitute),
and sampling
frame (new
school frame
or not).
type
of sampled
school (original
or substitute),
and sampling
frame (new
school frame
or not).
Computation of a student base weight reflects

 the
student's overall
probability of
selection accounting
for school
and student
sampling, assignment
to session
type at
the school-
and student-level,
and
the
student's overall
probability of
selection accounting
for school
and student
sampling, assignment
to session
type at
the school-
and student-level,
and
 the
student's assignment
to the
civics, geography,
U.S. history,
or technology
and engineering
literacy (TEL)
assessment.
the
student's assignment
to the
civics, geography,
U.S. history,
or technology
and engineering
literacy (TEL)
assessment.
School Base Weights Student Base Weights

NAEP Technical Documentation School Base Weights for the 2018 Assessment
The school base weight for a sampled school is equal to the inverse of its overall probability of selection.
The overall selection probability of a sampled school differs by

 type
of sampled
school (original
or substitute),
and sampling
frame (new
school frame
or not).
type
of sampled
school (original
or substitute),
and sampling
frame (new
school frame
or not).
 The
overall probability
of selection
of an
originally selected
school reflects
two components:
the probability
of selection
of the
primary sampling
unit (PSU),
and
The
overall probability
of selection
of an
originally selected
school reflects
two components:
the probability
of selection
of the
primary sampling
unit (PSU),
and
 the
probability of
selection of
the school
within the
selected PSU
from either
the NAEP
public school
frame or
the private
school frame.
the
probability of
selection of
the school
within the
selected PSU
from either
the NAEP
public school
frame or
the private
school frame.
 The
overall selection
probability of
a school
from the
new school
frame is
the product
of two
quantities: the
probability of
selection of
the school's
district into
the new-school
district sample,
and
The
overall selection
probability of
a school
from the
new school
frame is
the product
of two
quantities: the
probability of
selection of
the school's
district into
the new-school
district sample,
and
 the
probability of
selection of
the school
into the
new school
sample.
the
probability of
selection of
the school
into the
new school
sample.
Substitute public schools for the 2018 Social Sciences assessment
Substitute private schools for the 2018 Social Sciences assessment
Substitute public schools for the 2018 Technology and Engineering Literacy (TEL) assessment
Substitute private schools for the 2018 Technology and Engineering Literacy (TEL) assessment
The new-school district sampling procedure for the 2018 public school assessment in social sciences is very similar to the new-school district sampling procedure for the 2018 public school assessment in technology and engineering literacy (TEL).
Substitute schools are preassigned to original schools and take the place of original schools that refuse to participate. For weighting purposes, substitute schools are treated as if they were the original schools that they replaced, so they are assigned the school base weight of their original schools.

NAEP Technical Documentation Student Base Weights for the 2018 Assessment
Every sampled student received a student base weight, whether or not the student participated in the assessment. The student base weight is the reciprocal of the probability that the student was sampled to participate in the assessment for a specified subject. The student base weight for student k from school s in stratum j (STU_BWTjsk) is the product of seven weighting components and can be expressed as follows:
![]()
where







SCH_BWTjs is the school base weight;
SCHSsessionassignmentESWTjs is the school-level session assignment weight that reflects the conditional probability, given the school, that the particular session type was assigned to the school;
WINSCHWTjs is the within-school student weight that reflects the conditional probability, given the school, that the student was selected for the NAEP assessment;
STUSESWTjsk is Stu_bookmark the student-level session assignment weight that reflects the conditional probability, given the particular session type was assigned to the school, that the student was assigned to that session type;
SUBJFACjsk is the subject spiral adjustment factor that reflects the conditional probability, given the student was assigned to a particular session type, that the student was assigned the specified subject;
SUBADJjs is the substitution adjustment factor to account for the difference in enrollment size between the substitute and original school; and
YRRND_AFjs is the year-round adjustment factor to account for students in year-round schools on scheduled break at the time of the NAEP assessment and thus not available for sample.
The within-school student weight (WINSCHWTjs) is the inverse of the student sampling rate in the school.
The subject spiral adjustment factor (SUBJFACjsk) adjusts the student weight to account for the spiral pattern used in distributing civics, geography, U.S. history, or technology and engineering literacy (TEL) booklets to students. The subject factor varies by grade, subject, assessment mode (paper-based or digitally-based) and school type (public/private). It is equal to the inverse of the booklet proportions (civics, geography, U.S. history, or TEL) in the overall spiral for a specific sample.
For cooperating substitutes of nonresponding sampled original schools, the substitution adjustment factor (SUBADJjs) is equal to the ratio of the estimated grade enrollment for the originally sampled school to the estimated grade enrollment for the substitute school. The student sample from the substitute school then "represents" the set of grade-eligible students from the originally sampled school.
The year-round adjustment factor (YRRND_AFjs) adjusts the student weight for students in year-round schools who do not attend school during the time of the assessment. This situation typically arises in overcrowded schools. School administrators in year-round schools randomly assign students to portions of the year in which they attend school and portions of the year in which they do not attend. At the time of assessment, a certain percentage of students (designated as OFFjs) do not attend school and thus cannot be assessed. The YRRND_AFjs for a school is calculated as 1 / (1 - OFFjs / 100).

NAEP Technical Documentation School and Student Nonresponse Weight Adjustments for the 2018 Assessment
Nonresponse is unavoidable in any voluntary survey of a human population. Nonresponse leads to the loss of sample data that must be compensated for in the weights of the responding sample members. This differs from ineligibility, for which no adjustments are necessary. The purpose of the nonresponse adjustments is to reduce the mean square error of survey estimates. While the nonresponse adjustment reduces the bias from the loss of sample, it also increases variability among the survey weights leading to increased variances. However, it is presumed that the reduction in bias more than compensates for the increase in the variance, thereby reducing the mean square error and thus improving the accuracy of survey estimates. Nonresponse adjustments are made in the NAEP surveys at both the
School Nonresponse Weight Adjustment
Student Nonresponse Weight Adjustment
school and the student levels: the responding (original and substitute) schools receive a weighting adjustment to compensate for nonresponding schools, and responding students receive a weighting adjustment to compensate for nonresponding students.
The paradigm used for nonresponse adjustment in NAEP is the quasi-randomization approach (Oh and Scheuren 1983). In this approach, school response cells are based on characteristics of schools known to be related to both response propensity and achievement level, such as the urbanization classification (e.g., city of a metropolitan area) of the school. Likewise, student response cells are based on characteristics of the schools containing the
students and student characteristics that are known to be related to both response propensity and achievement level, such as student race/ethnicity, gender, and age.
Under this approach, sample members are assigned to mutually exclusive and exhaustive response cells based on predetermined characteristics. A nonresponse adjustment factor is calculated for each cell as the ratio of the sum of adjusted base weights for all eligible units to the sum of adjusted base weights for all responding units. The nonresponse adjustment factor is then applied to the base weight of each responding unit. In this way, the weights of responding units in the cell are "weighted up" to represent the full set of responding and nonresponding units in the response cell.
The quasi-randomization paradigm views nonresponse as another stage of sampling. Within each nonresponse cell, the paradigm assumes that the responding sample units are a simple random sample from the total set of all sample units. If this model is valid, then the use of the quasi-randomization weighting adjustment will eliminate any nonresponse bias. Even if this model is not valid, the weighting adjustments will eliminate bias if the achievement scores are homogeneous within the response cells. That is, bias is eliminated if there is homogeneity either in response propensity or in achievement levels. If neither the response propensity nor the achievement scores are perfectly homogeneous, nonresponse weight adjustments will reduce bias if the characteristics that define nonresponse cells are related to both achievement and response propensity. See, for example, chapter 4 of Little and Rubin (1987).

NAEP Technical Documentation School Nonresponse Weight Adjustment for the 2018 Assessment
The school nonresponse adjustment procedure inflates the weights of participating schools to account for eligible nonparticipating schools for which no substitute schools participated. The adjustments are computed within nonresponse cells and are based on the assumption that the participating and nonparticipating schools within the same cell are more similar to one another than to schools from different cells. Nonresponse cell definitions varied for public and private schools.
Development of Initial School Nonresponse Cells
Development of Final School Nonresponse Cells
School Nonresponse Adjustment Factor Calculation
NAEP Technical Documentation Development of Final School Nonresponse Cells for the 2018 Assessment
Limits were placed on the magnitude of cell sizes and adjustment factors to prevent unstable nonresponse adjustments and unacceptably large nonresponse factors. All initial weighting cells with fewer than six cooperating schools or adjustment factors greater than three for the full sample weight were collapsed with suitable adjacent cells. Simultaneously, all initial weighting cells for any replicate with fewer than four cooperating schools or adjustment factors greater than the maximum of three (or two times the full sample nonresponse adjustment factor) were collapsed with suitable adjacent cells. Initial weighting cells were generally collapsed in reverse order of the cell structure; that is, starting at the bottom of the nesting structure and working up toward the top level of the nesting structure.
Public Schools
For the public schools, race/ethnicity classification cells (categories based on the total percentage of Black, Hispanic, and American Indian/Alaska Native students) within an urbanization classification (four categories based on urban-centric locale) stratum and census region were collapsed first. If further collapsing was required after all levels of race/ethnicity cells were collapsed, urbanization strata within census region were combined next. Cells were never collapsed across census region.
Private Schools
For the private schools, urbanization classification strata within a census region and affiliation type were collapsed first. If further collapsing was required, census region cells within an affiliation type were collapsed. Cells were never collapsed across affiliation.

NAEP Technical Documentation Development of Initial School Nonresponse Cells for the 2018 Assessment
The cells for nonresponse adjustments are generally functions of the school sampling strata. Sampling strata definitions differ for public and private schools.
Public Schools
 For
public school
samples, initial
weighting cells
were formed
using the
following nesting
cell structure:
census region,
For
public school
samples, initial
weighting cells
were formed
using the
following nesting
cell structure:
census region,
 urbanization
classification (four
categories based
on urban-centric
locale) stratum,
and
urbanization
classification (four
categories based
on urban-centric
locale) stratum,
and
 race/ethnicity
classification (categories
based on
the total
percentage of
Black, Hispanic,
and American
Indian/Alaska Native
students).
race/ethnicity
classification (categories
based on
the total
percentage of
Black, Hispanic,
and American
Indian/Alaska Native
students).
Private Schools
 For
private school
samples, initial
weighting cells
were formed
using the
following nesting
cell structure:
affiliation (Catholic
or non-Catholic),
For
private school
samples, initial
weighting cells
were formed
using the
following nesting
cell structure:
affiliation (Catholic
or non-Catholic),
 census
region, and
census
region, and
 urbanization
classification (four
categories based
on urban-centric
locale) stratum.
urbanization
classification (four
categories based
on urban-centric
locale) stratum.

NAEP Technical Documentation School Nonresponse Adjustment Factor Calculation for the 2018 Assessment
In each final school nonresponse adjustment cell c, the school nonresponse adjustment factor SCH_NRAFc was computed as follows:
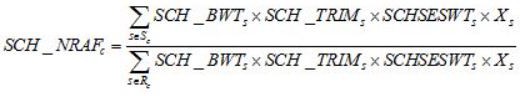
where
 Sc
is the
set of
all eligible
sampled schools
(cooperating original
and substitute
schools and
refusing original
schools with
noncooperating or
no assigned
substitute) in
cell c,
Sc
is the
set of
all eligible
sampled schools
(cooperating original
and substitute
schools and
refusing original
schools with
noncooperating or
no assigned
substitute) in
cell c,

 Rc
is the set of all cooperating schools within Sc,
SCH_BWTs
is the
school base
weight,
Rc
is the set of all cooperating schools within Sc,
SCH_BWTs
is the
school base
weight,
 SCH_TRIMs
is the
school-level weight
trimming factor,
SCH_TRIMs
is the
school-level weight
trimming factor,
 SCHSESWTs
is the
school-level session
assignment weight,
and
SCHSESWTs
is the
school-level session
assignment weight,
and
 Xs
is the
estimated grade
enrollment corresponding
to the
original sampled
school.
Xs
is the
estimated grade
enrollment corresponding
to the
original sampled
school.

NAEP Technical Documentation Student Nonresponse Weight Adjustment for the 2018 Assessment
The student nonresponse adjustment procedure inflates the weights of assessed students to account for eligible sampled students who did not participate in the assessment. These inflation factors offset the loss of data associated with absent students. The adjustments are computed within nonresponse cells and are based on the assumption that the assessed and absent students within the same cell are more similar to one another than to students from different cells. Like its counterpart at the school level, the student nonresponse adjustment is intended to reduce the mean square error and thus improve the accuracy of NAEP assessment estimates.
Development of Initial Student Nonresponse Cells
Development of Final Student Nonresponse Cells
Student Nonresponse Adjustment Factor Calculation
NAEP Technical Documentation Development of Final Student Nonresponse Cells for the 2018 Assessment
Similar to the school nonresponse adjustment, cell and adjustment factor size constraints are in place to prevent unstable nonresponse adjustments or unacceptably large adjustment factors. All initial weighting cells with either fewer than 20 participating students, or adjustment factors greater than two for the full sample weight, were collapsed with suitable adjacent cells. Simultaneously, all initial weighting cells for any replicate with either fewer than 15 participating students or an adjustment factor greater than the maximum of two or one and a half times the full sample nonresponse adjustment factor were collapsed with suitable adjacent cells. Initial weighting cells were generally collapsed in reverse order of the cell structure; that is, starting at the bottom of the nesting structure and working up toward the top level of the nesting structure.
Public Schools
For public schools, race/ethnicity cells within students with disabilities/English learners (SD/EL) status and subject, school nonresponse cell, age, and gender classes were collapsed first. If further collapsing was required, cells were next combined across gender, then age, and finally school nonresponse cells. Cells for public schools are never collapsed across SD/EL status and subject.
Private Schools
For private schools, race/ethnicity cells within school nonresponse cell, age, and gender classes were collapsed first. If further collapsing was required, cells were next combined across gender, then age, and finally school nonresponse cells.

NAEP Technical Documentation Development of Initial Student Nonresponse Cells for the 2018 Assessment
Cell definitions for the student nonresponse adjustment vary by public and private schools.
Public Schools
 The
public school
samples formed
initial student
nonresponse cells
using the
following nesting
cell structure:
students with
disabilities (SD)/English
learners (EL)
by subject,
The
public school
samples formed
initial student
nonresponse cells
using the
following nesting
cell structure:
students with
disabilities (SD)/English
learners (EL)
by subject,
 school
nonresponse cell,
school
nonresponse cell,

 relative
age1
(classified
into "older"
student and
"modal age
or younger"
student), gender,
and
relative
age1
(classified
into "older"
student and
"modal age
or younger"
student), gender,
and
 race/ethnicity.
race/ethnicity.
The highest level variable in the cell structure separates students who were classified either as with disabilities (SD) or as English learners (EL) from those who are neither, since SD or EL students tend to score lower on assessment tests than those without these limitations. In addition, the SD/EL categories are further broken down by subject since rules for excluding students from the assessment differ by subject. Non-SD/EL students are not broken down by subject because the exclusion rules do not apply to them.
Private Schools
 The
private school
samples formed
initial student
nonresponse cells
using the
following nesting
cell structure:
school nonresponse
cell,
The
private school
samples formed
initial student
nonresponse cells
using the
following nesting
cell structure:
school nonresponse
cell,

 relative
age1
(classified
into "older"
student and
"modal age
or younger"
student), gender,
and
relative
age1
(classified
into "older"
student and
"modal age
or younger"
student), gender,
and
 race/ethnicity.
race/ethnicity.
The structure for private school cells for student nonresponse is slightly different from public school cells. SD/EL status is not included in the private school cell structure because very few students (between 5-8 percent) in private schools are classified as SD/EL.
1 Older students in the grade 8 assessment are those born before October 1, 2003. Students born after that date are classified as modal age or younger.

NAEP Technical Documentation Student Nonresponse Adjustment Factor Calculation for the 2018 Assessment
In each final student nonresponse adjustment cell c for a given sample, the student nonresponse adjustment factor STU_NRAFc was computed as follows:

where






Sc is the set of all eligible sampled students in cell c for a given sample,
Rc is the set of all assessed students within Sc,
STU_BWTk is the student base weight for a given student k,
SCH_TRIMk is the school-level weight trimming factor for the school associated with student k, SCH_NRAFk is the school-level nonresponse adjustment factor for the school associated with student k, and SUBJFACk is the subject factor for a given student k.
The student weight used in the calculation above is the adjusted student base weight, without regard to subject, adjusted for school weight trimming and school nonresponse.
Nonresponse adjustment procedures are not applied to excluded students because they are not required to complete an assessment. In effect, excluded students were placed in a separate nonresponse cell by themselves and all received an adjustment factor of one. While excluded students are not included in the analysis of the NAEP scores, weights are provided for excluded students in order to estimate the size of this group and its population characteristics.

NAEP Technical Documentation School and Student Weight Trimming Adjustments for the 2018 Assessment
Weight trimming is an adjustment procedure that involves detecting and reducing extremely large weights. "Extremely large weights" generally refer to large sampling weights that were not anticipated in the design of the sample. Unusually large weights are likely to produce large sampling variances for statistics of interest, especially when the large weights are associated with sample cases reflective of rare or atypical characteristics. To reduce the impact of these large weights on variances, weight reduction methods are typically employed. The goal of weight reduction methods is to reduce the mean square error of survey estimates. While the trimming of large weights
Trimming of School Base Weights
Trimming of Student Weights
reduces variances, it also introduces some bias. However, it is presumed that the reduction in the variances more than compensates for the increase in the bias, thereby reducing the mean square error and thus improving the accuracy of survey estimates (Potter 1988). NAEP employs weight trimming at both the school and student levels.

NAEP Technical Documentation Trimming of School Base Weights for the 2018 Assessment
Large school weights can occur for public schools selected from the NAEP new-school sampling frame and for private schools. New schools that are eligible for weight trimming are public schools with a disproportionately large student enrollment in a particular grade from a school district that was selected with a low probability of selection. The school base weights for such schools may be large relative to what they would have been if they had been selected as part of the original sample.
To detect extremely large weights among new schools, a comparison was made between a new school's school base weight and its ideal weight (i.e., the weight that would have resulted had the school been selected from the original school sampling frame). If the school base weight was more than three times the ideal weight, a trimming factor was calculated for that school that scaled the base weight back to three times the ideal weight. The calculation of the school-level trimming factor for a new school s is expressed in the following formula:
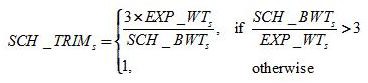
where


EXP_WTs is the ideal base weight the school would have received if it had been on the NAEP public school sampling frame, and
SCH_BWTs is the actual school base weight the school received as a sampled school from the new school frame.
No new schools in the NAEP 2018 sample had their weights trimmed.
Private schools eligible for weight trimming were Private School Universe Survey (PSS) nonrespondents who were found subsequently to have either larger enrollments than assumed at the time of sampling, or an atypical probability of selection given their affiliation, the latter being unknown at the time of sampling. For private school s, the formula for computing the school-level weight trimming factor SCH_TRIMs is identical to that used for new schools. For private schools,
 EXP_WTs
is the
ideal base
weight the
school would
have received
if it
had been
on the
NAEP private
school sampling
frame with
accurate enrollment
and known
affiliation, and
EXP_WTs
is the
ideal base
weight the
school would
have received
if it
had been
on the
NAEP private
school sampling
frame with
accurate enrollment
and known
affiliation, and
 SCH_BWTs
is the
actual school
base weight
the school
received as
a sampled
private school.
SCH_BWTs
is the
actual school
base weight
the school
received as
a sampled
private school.
No private schools in the NAEP 2018 sample had their weights trimmed.

NAEP Technical Documentation Trimming of Student Weights for the 2018 Assessment
Large student weights generally come from compounding nonresponse adjustments at the school and student levels with artificially low first-stage selection probabilities, which can result from inaccurate enrollment data on the school frame used to define the school size measure. Even though
measures are in place to limit the number and size of excessively large weights—such as the implementation of adjustment factor size constraints in both the school and student nonresponse procedures and the use of the school trimming procedure—large student weights can still occur due to compounding effects of various weighting components.
The student weight trimming procedure uses a multiple median rule to detect excessively large student weights. Any student weight within a given trimming group greater than a specified multiple of the median weight value of the given trimming group has its weight scaled back to that threshold. Trimming groups were defined by region and high minority (American Indian/Alaska Native, or Black/Hispanic) strata for public schools and affiliation (Catholic/non-Catholic) for private schools.
The procedure computes the median of the nonresponse-adjusted student weights in the trimming group g for a given grade and subject sample. Any student k with a weight more than M times the median (where M = 3.5 for public and private schools) received a trimming factor calculated as follows:
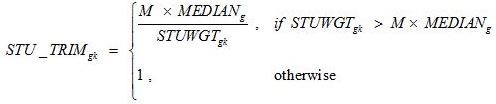
where



M is the trimming multiple,
MEDIANg is the median of nonresponse-adjusted student weights in trimming group g, and
STUWGTgk is the weight after student nonresponse adjustment for student k in trimming group g.
In the 2018 NAEP assessment, relatively few students had weights considered excessively large. Out of the approximately 59,100 students in the combined 2018 assessment samples, approximately 200 students had their weights trimmed.

NAEP Technical Documentation Student Weight Raking Adjustment for the 2018 Assessment
Development of Final Raking Dimensions
Weighted estimates of population totals for student-level subgroups for a given grade will vary across subjects even though the student samples for each subject generally come from the same schools. These differences are the result of sampling error associated with the random assignment of subjects to students through a process known as spiraling. Any difference in demographic estimates between subjects, no matter how small, may raise concerns about data quality. To remove
Raking Adjustment Control Totals Raking Adjustment Factor Calculation
these random differences and potential data quality concerns, a step was added to the NAEP weighting procedure in 2009. This step adjusts the student weights in such a way that the weighted sums of population totals for specific student groups are the same across all subjects. It was implemented using a raking procedure and applied only to public school assessments.
Raking is a weighting procedure based on the iterative proportional fitting process developed by Deming and Stephan (1940) and involves simultaneous ratio adjustments to two or more marginal distributions of population totals. Each set of marginal population totals is known as a dimension, and each population total in a dimension is referred to as a control total. Raking is carried out in a sequence of adjustments. Sampling weights are adjusted to one marginal distribution and then to the second marginal distribution, and so on. One cycle of sequential adjustments to the marginal distributions is called an iteration. The procedure is repeated until convergence is achieved. The criterion for convergence can be specified either as the maximum number of iterations or an absolute difference (or relative absolute difference) from the marginal population totals. More discussion on raking can be found in Oh and Scheuren (1987).
For NAEP 2018, the student raking adjustment was carried out separately for the geography and U.S. history public school samples at grade 8. The dimensions used in the raking process were race/ethnicity, SD/EL status, and gender. The control totals for the raking dimensions for both subject-based samples (i.e., geography and U.S. history) for grade 8 were obtained from summing the combined DBA/PBA student sample weights of the geography and U.S. history public school samples combined.

NAEP Technical Documentation Development of Final Raking Dimensions for the 2018 Assessment
The raking procedure involved three dimensions. The variables used to define the dimensions are listed below along with the categories making up the initial raking cells for each dimension.
Race/Ethnicity
White, not Hispanic
Black, not Hispanic
Hispanic
Asian
American Indian/Alaska Native
Native Hawaiian/Pacific Islander
Two or More Races
SD/EL status
SD, but not EL
EL, but not SD
SD and EL
Neither SD nor EL
Gender
Male
Female
The initial cells were created at the national level. Similar to the procedure used for school and student nonresponse adjustments, limits were placed on the magnitude of the cell sizes and adjustment factors to prevent unstable raking adjustments that could have resulted in unacceptably large or small adjustment factors. Levels of a dimension were combined whenever there were fewer than 30 assessed or excluded students (20 for any of the replicates) in a category, if the smallest adjustment was less than 0.5, or if the largest adjustment was greater than 2 for the full sample or for any replicate.
If collapsing was necessary for the race/ethnicity dimension, individual groups with similar student achievement levels were combined first. If further collapsing was necessary, the next closest race/ethnicity group was combined as well, and so on until all collapsing rules were satisfied. In some instances, all seven categories had to be collapsed.
If collapsing was necessary for the SD/EL dimension, the SD/not EL and SD/EL categories were combined first, followed by EL/not SD if further collapsing was necessary. In some instances, all four categories had to be collapsed.
Collapsing gender is generally not expected. However, in the rare event that it is necessary, male and female categories would be collapsed.

NAEP Technical Documentation Raking Adjustment Control Totals for the 2018 Assessment
The control totals used in the raking procedure for NAEP 2018 at grade 8 were estimates of the student population derived from the set of assessed and excluded students pooled across subjects (geography and U.S. history) and assessment modes (PBA and DBA). The control totals for category c within dimension d were computed as follows:
![]()
where







Rc(d) is the set of all assessed students in category c of dimension d,
Ec(d) is the set of all excluded students in category c of dimension d, STU_BWTk is the student base weight for a given student k,
SCH_TRIMk is the school-level weight trimming factor for the school associated with student k, SCH_NRAFk is the school-level nonresponse adjustment factor for the school associated with student k, STU_NRAFk is the student-level nonresponse adjustment factor for student k, and
SUBJFACk is the subject factor for student k.
The student weight used in the calculation of the control totals above is the adjusted student base weight, without regard to subject, adjusted for school weight trimming, school nonresponse, and student nonresponse. Control totals were computed for the full sample and for each replicate independently.

NAEP Technical Documentation Raking Adjustment Factor Calculation for the 2018 Assessment
For assessed and excluded students in a given subject, the raking adjustment factor STU_RAKEk was computed as below. First, the weight for student k was initialized as follows:
![]()
where





STU_BWTk is the student base weight for a given student k
SCH_TRIMk is the school-level weight trimming factor for the school associated with student k SCH_NRAFk is the school-level nonresponse adjustment factor for the school associated with student k, STU_NRAFk is the student-level nonresponse adjustment factor for student k, and
SUBJFACk is the subject factor for student k.
Then, the sequence of weights for the first iteration was calculated as follows for student k in category c of dimension d: For dimension 1:
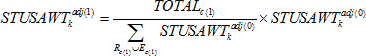
For dimension 2:
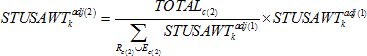
For dimension 3:

where



Rc(d) is the set of all assessed students in category c of dimension d, Ec(d) is the set of all excluded students in category c of dimension d, and Totalc(d) is the control total for category c of dimension d.
The process is said to converge if the maximum difference between the sum of adjusted weights and the control totals is 1.0 for each category in each dimension. If after the sequence of adjustments the maximum difference was greater than 1.0, the process continues to the next iteration, cycling back to the first dimension with the initial weight for student k equaling STUSAWTkadj(3) from the previous iteration. The process continued until convergence was reached.
Once the process converged, the adjustment factor was computed as follows:
![]()
where

STUSAWTk is the weight for student k after convergence.
The process was done independently for the full sample and for each replicate.

NAEP Technical Documentation Computation of Replicate School Weights for Variance Estimation for the 2018 Assessment
In addition to the full-sample weight, a set of 62 replicate weights was provided for each school. These replicate weights are used in calculating the sampling variance of estimates obtained from the data, using the jackknife repeated replication method. The method of deriving these weights was aimed at reflecting the features of the sample design appropriately for each sample, so that when the jackknife variance estimation procedure is implemented, approximately unbiased estimates of sampling variance are obtained. This section gives the specifics for generating the replicate weights for the 2018 assessment samples.
For each sample, replicates were formed in two steps. First, each school was assigned to one or more of 62 replicate strata. In the next step, a random subset of schools in each replicate stratum was excluded. The remaining subset and all schools in the other replicate strata then constituted one of the 62 replicates.
Defining Replicate Strata and Forming Replicates
A replicate weight was calculated for each of the 62 replicates using weighting procedures similar to those used for the full-sample weight. Each replicate base weight contains an additional component, known as a replicate factor, to account for the subsetting of the sample to form the replicate. By repeating the various weighting procedures on each set of replicate base weights, the impact of these procedures on the sampling variance of an estimate is appropriately reflected in the variance estimate.
Each of the 62 replicate weights for school s in stratum j can be expressed as follows:
![]()
where




SCH_BWTjs(r) is the replicate school base weight for replicate r SCH_NRAFjs(r) is the school-level nonresponse adjustment factor for replicate r SCH_TRIMjs is the school-level weight trimming adjustment factor; and SCH_SUBJ_AFs is the small-school subject adjustment factor.
Specific school nonresponse adjustment factors were calculated separately for each replicate, as indicated by the index (r) in the formula, and applied to the replicate school base weights. Computing separate nonresponse adjustment factors for each replicate allows resulting variances from the use of the final school replicate weights to reflect components of variance due to this weight adjustment.
School weight trimming adjustments were not replicated, that is, not calculated separately for each replicate. Instead, each replicate used the school trimming adjustment factors derived for the full sample. Statistical theory for replicating trimming adjustments under the jackknife approach has not been developed in the literature. Due to the absence of a statistical framework, and since relatively few school weights in NAEP require trimming, the weight trimming adjustments were not replicated.
In addition, the small-school subject adjustment factor also used the same factor derived for the full sample.

NAEP Technical Documentation Computation of Replicate Student Weights for Variance Estimation for the 2018 Assessment
In addition to the full-sample weight, a set of 62 replicate weights was provided for each student. These replicate weights are used in calculating the sampling variance of estimates obtained from the data, using the jackknife repeated replication method. The method of deriving these weights was aimed at reflecting the features of the sample design appropriately for each sample, so that when the jackknife variance estimation procedure is implemented, approximately unbiased estimates of sampling variance are obtained. This section gives the specifics for generating the replicate weights for the 2018 assessment samples. The theory that underlies the jackknife variance estimators used in NAEP studies is discussed in the section Replicate Variance Estimation.
For each sample, replicates were formed in two steps. First, each school was assigned to one or more of 62 replicate strata. In the next step, a random subset of schools (or, in some cases, students within
Defining Replicate Strata and Forming Replicates
Computing School-Level Replicate Base Weights
Computing Student-Level Replicate Base Weights
Replicate Variance Estimation
schools) in each replicate stratum was excluded. The remaining subset and all schools in the other replicate strata then constituted one of the 62 replicates.
A replicate weight was calculated for each of the 62 replicates using weighting procedures similar to those used for the full-sample weight. Each replicate base weight contains an additional component, known as a replicate factor, to account for the subsetting of the sample to form the replicate. By repeating the various weighting procedures on each set of replicate base weights, the impact of these procedures on the sampling variance of an estimate is appropriately reflected in the variance estimate.
Each of the 62 replicate weights for student k in school s and stratum j can be expressed as follows:
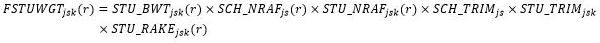
where






STU_BWTjsk(r) is the student base weight for replicate r;
SCH_NRAFjs(r) is the school-level nonresponse adjustment factor for replicate r; STU_NRAFjsk(r) is the student-level nonresponse adjustment factor for replicate r; SCH_TRIMjs is the school-level weight trimming adjustment factor;
STU_TRIMjsk is the student-level weight trimming adjustment factor; and
STU_RAKEjsk(r) is the student-level raking adjustment factor for replicate r.
Specific school and student nonresponse and student-level raking adjustment factors were calculated separately for each replicate, as indicated by the index (r) in the formula, and applied to the replicate student base weights. Computing separate nonresponse and raking adjustment factors for each replicate allows resulting variances from the use of the final student replicate weights to reflect components of variance due to these various weight adjustments.
School and student weight trimming adjustments were not replicated, that is, not calculated separately for each replicate. Instead, each replicate used the school and student trimming adjustment factors derived for the full sample. Statistical theory for replicating trimming adjustments under the jackknife approach has not been developed in the literature. Due to the absence of a statistical framework, and since relatively few school and student weights in NAEP require trimming, the weight trimming adjustments were not replicated.

NAEP Technical Documentation Computing School-Level Replicate Base Weights for the 2018 Assessment
For the NAEP 2018 assessment, school-level replicate base weights for school s in primary stratum j (SCH_BWTjs(r), r = 1,..., 62) were calculated as follows:
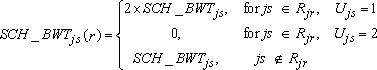
where



SCH_BWTjs is the school base weight for school s in primary stratum j,
Rjr is the set of schools within the r-th replicate stratum for primary stratum j, and
Ujs is the variance unit (1 or 2) for school s in primary stratum j.
For schools in replicate strata comprising three variance units, two sets of school-level replicate base weights were computed (see replicate variance estimation for details): one for the first replicate r1 and another for the second replicate r2. The two sets of school-level replicate base weights SCH_BWTjs(r1), r1 = 1,..., 62 and SCH_BWTjs(r2), r2 = 1,..., 62 were calculated as described below.
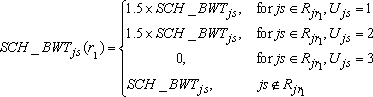

where




SCH_BWTjs is the school base weight for school s in primary stratum j,
Rjr1 is the set of schools within the r1-th replicate stratum for primary stratum j, Rjr2 is the set of schools within the r2-th replicate stratum for primary stratum j, and Ujs is the variance unit (1, 2, or 3) for school s in primary stratum j.

NAEP Technical Documentation Computing Student-Level Replicate Base Weights for the 2018 Assessment
For the 2018 assessment, the calculation of the student-level replicate base weights for student k from school s in stratum j for each of the 62 replicates,
STU_BWTjsk(r), where r = 1 to 62, were calculated as follows:
![]()
where







SCH_BWTjs(r) is the replicate school base weight;
SCHSESWTjs is the school-level session assignment weight used in the full-sample weight; WINSCHWTjs is the within-school student sampling weight used in the full-sample weight; STUSESWTjsk is the student-level session assignment weight used in the full-sample weight; SUBJFACjs is the subject factor used in the full-sample weight;
SUBADJjs is the substitute adjustment factor used in the full-sample weight; and
YRRND_AFjs is the year-round adjustment factor used in the full-sample weight.
These components are described on the Student Base Weights page.

NAEP Technical Documentation Defining Replicate Strata and Forming Replicates for the 2018 Assessment
For the NAEP 2018 assessment, replicates were formed separately for each sample indicated by grade (8) and subject (civics/geography/U.S. history or TEL). The first step in forming replicates was to assign each first-stage sampling unit in a primary stratum to a replicate stratum. The formation of replicate strata varied by noncertainty and certainty primary sampling units (PSUs). For noncertainty PSUs, the first-stage units were PSUs, and the
primary stratum was the combination of region and metropolitan status. For certainty PSUs, the first-stage units were schools, and the primary stratum was school type (public or private).
Civics/Geography/U.S. History Assessments
For noncertainty PSUs, where only one PSU was selected per PSU stratum, replicate strata were formed by pairing sampled PSUs with similar stratum characteristics within the same primary stratum (region by metropolitan status). This was accomplished by first sorting the 76 sampled PSUs by PSU stratum number and then grouping adjacent PSUs into 38 pairs. The values for a PSU stratum number reflect region and metropolitan status, as well as socioeconomic characteristics such as percent of renters and percentage of children below the poverty line. The formation of these replicate strata in this manner models a design of selecting two PSUs with probability proportional to size with replacement from each of 38 strata.
For certainty PSUs, the first stage of sampling is at the school level, and the formation of replicate strata must reflect the sampling of schools within the certainty PSUs. Replicate strata were formed by sorting the sampled schools in the 29 certainty PSUs by their order of selection within a primary stratum (school type) so that the sort order reflected the implicit stratification (region, urbanization classification, race/ethnicity classification, and student enrollment for public schools; and region, private school type, and student enrollment size for private schools) and systematic sampling features of the sample design.
The first-stage units were then paired off into 24 preliminary replicate strata. Within each primary stratum with an even number of first-stage units, all of the preliminary replicate strata were pairs, and within primary strata with an odd number of first-stage units, one of the replicate strata was a triplet (the last one), and all others were pairs.
If there were more than 24 preliminary replicate strata within a primary stratum, the preliminary replicate strata were grouped to form 24 replicate strata. This grouping effectively maximized the distance in the sort order between grouped preliminary replicate strata. The first 24 preliminary replicate strata, for example, were assigned to 24 different final replicate strata in order (1 through 24), with the next 24 preliminary replicate strata assigned to final replicate strata 1 through 24, so that, for example, preliminary replicate stratum 1, preliminary replicate stratum 25, preliminary replicate stratum 49 (if there were that many), etc., were all assigned to the first final replicate stratum. The final replicate strata for the schools in the certainty PSUs were 1 through 24.
Within each pair of preliminary replicate stratum, the first first-stage unit was assigned as the first variance unit and the second first-stage unit as the second variance unit. Within each triplet preliminary replicate stratum, the three schools were assigned variance units 1 through 3.
TEL Assessment
For noncertainty PSUs, where only one PSU was selected per PSU stratum, replicate strata were formed by pairing sampled PSUs with similar stratum characteristics within the same primary stratum (region by metropolitan status). This was accomplished by first sorting the 38 sampled PSUs by PSU stratum number and then grouping adjuacent PSUs into 19 pairs. The values for a PSU stratum number reflect region and metropolitan status, as well as socioeconomic characteristics such as percent of renters and percentage of children below the poverty line. The formation of these replicate strata in this manner models a design of selecting two PSUs with probability proportional to size with replacement from each of 19 strata.
For certainty PSUs, the first stage of sampling is at the school level, and the formation of replicate strata must reflect the sampling of schools within the certainty PSUs. Replicate strata were formed by sorting the sampled schools in the 29 certainty PSUs by their order of selection within a primary stratum (school type) so that the sort order reflected the implicit stratification (region, urbanization classification, race/ethnicity classification, and student
enrollment for public schools; and region, private school type, and student enrollment size for private schools) and systematic sampling features of the sample design.
The first-stage units were then paired off into 43 preliminary replicate strata. Within each primary stratum with an even number of first-stage units, all of the preliminary replicate strata were pairs, and within primary strata with an odd number of first-stage units, one of the replicate strata was a triplet (the last one), and all others were pairs.
If there were more than 43 preliminary replicate strata within a primary stratum, the preliminary replicate strata were grouped to form 43 replicate strata. This grouping effectively maximized the distance in the sort order between grouped preliminary replicate strata. The first 43 preliminary replicate strata, for example, were assigned to 43 different final replicate strata in order (1 through 43), with the next 43 preliminary replicate strata assigned to final replicate strata 1 through 43, so that, for example, preliminary replicate stratum 1, preliminary replicate stratum 44, preliminary replicate stratum 87 (if there were that many), etc., were all assigned to the first final replicate stratum. The final replicate strata for the schools in the certainty PSUs were 1 through 43.
Within each pair of preliminary replicate stratum, the first first-stage unit was assigned as the first variance unit and the second first-stage unit as the second variance unit. Within each triplet preliminary replicate stratum, the three schools were assigned variance units 1 through 3.

NAEP Technical Documentation Replicate Variance Estimation for the 2018 Assessment
Variances for NAEP assessment estimates are computed using the paired jackknife replicate variance procedure. This technique is applicable for common statistics, such as means and ratios, and differences between these for different subgroups, as well as for more complex statistics such as linear or logistic regression coefficients.
In general, the paired jackknife replicate variance procedure involves initially pairing clusters of first-stage sampling units to form H variance strata (h = 1, 2, 3, ...,H) with two units per stratum. The first replicate is formed by assigning, to one unit at random from the first variance stratum, a replicate weighting factor of less than 1.0, while assigning the remaining unit a complementary replicate factor greater than 1.0, and assigning all other units from the other (H - 1) strata a replicate factor of 1.0. This procedure is carried out for each variance stratum resulting in H replicates, each of which provides an estimate of the population total.
In general, this process is repeated for subsequent levels of sampling. In practice, this is not practicable for a design with three or more stages of sampling, and the marginal improvement in precision of the variance estimates would be negligible in all such cases in the NAEP setting. Thus in NAEP,
when a two-stage design is used – sampling schools and then students – beginning in 2011 replication is carried out at both stages for the purpose of computing replicate student weights. The change implemented in 2011 permitted the introduction of a finite population correction factor at the school sampling stage. Prior to 2011, replication was only carried out at the first stage of selection for the purpose of computing replicate student weights. See Rizzo and Rust (2011) for a description of the methodology.
When a three-stage design is used, involving the selection of geographic primary sampling units (PSUs), then schools, and then students, the replication procedure for the purpose of computing replicate student weights is only carried out at the first stage of sampling (the PSU stage for noncertainty PSUs, and the school stage within certainty PSUs). In this situation, the school and student variance components are correctly estimated, and the overstatement of the between-PSU variance component is relatively very small.
The jackknife estimate of the variance for any given statistic is given by the following formula:
![]()
where

![]()

![]() represents
the full
sample estimate
of the
given statistic,
and represents
the corresponding
estimate for
replicate h.
represents
the full
sample estimate
of the
given statistic,
and represents
the corresponding
estimate for
replicate h.
Each replicate undergoes the same weighting procedure as the full sample so that the jackknife variance estimator reflects the contributions to or reductions in variance resulting from the various weighting adjustments.
The NAEP jackknife variance estimator is based on 62 variance strata resulting in a set of 62 replicate weights assigned to each school and student.
The basic idea of the paired jackknife variance estimator is to create the replicate weights so that use of the jackknife procedure results in an unbiased variance estimator for sample totals and means, which is also reasonably efficient (i.e., has a low variance as a variance estimator). The jackknife variance estimator will then produce a consistent (but not fully unbiased) estimate of variance for (sufficiently smooth) nonlinear functions of total and mean estimates such as ratios, regression coefficients, and so forth (Shao and Tu, 1995).
The development below shows why the NAEP jackknife variance estimator returns an unbiased variance estimator for totals and means, which is the cornerstone to the asymptotic results for nonlinear estimators. For example, see Rust (1985). This paper also discusses why this variance estimator is generally efficient (i.e., more reliable than alternative approaches requiring similar computational resources).
The development is done for an estimate of a mean based on a simplified sample design that closely approximates the sample design for first-stage units used in the NAEP studies. The sample design is a stratified random sample with H strata with population weights Wh, stratum sample sizes nh, and
![]()
![]() stratum
sample means
. The
population estimator
and
standard unbiased
variance estimator
stratum
sample means
. The
population estimator
and
standard unbiased
variance estimator
![]() are:
are:
![]()
with
![]()
![]() The
paired jackknife replicate variance estimator assigns one replicate
h=1,…, H to each stratum, so that the number of
replicates equals H. In NAEP,
the replicates correspond generally to pairs and triplets
(with the latter only being used if there are an odd number of sample
units within a particular primary
stratum generating replicate strata). For pairs, the process of
generating replicates can be viewed as taking a simple random sample
(J) of size nh/2
within the replicate stratum, and assigning an increased weight to
the sampled elements, and a decreased weight to the unsampled
elements. In certain
applications, the
increased weight
is double
the full
sample weight,
while the
decreased weight
is in
fact equal
to zero.
In this
simplified case,
this
The
paired jackknife replicate variance estimator assigns one replicate
h=1,…, H to each stratum, so that the number of
replicates equals H. In NAEP,
the replicates correspond generally to pairs and triplets
(with the latter only being used if there are an odd number of sample
units within a particular primary
stratum generating replicate strata). For pairs, the process of
generating replicates can be viewed as taking a simple random sample
(J) of size nh/2
within the replicate stratum, and assigning an increased weight to
the sampled elements, and a decreased weight to the unsampled
elements. In certain
applications, the
increased weight
is double
the full
sample weight,
while the
decreased weight
is in
fact equal
to zero.
In this
simplified case,
this
![]() assignment
reduces to
replacing with , the
latter being
the sample
mean of
the sampled
nh/2
units. Then
the replicate
estimator corresponding
to stratum
r is
assignment
reduces to
replacing with , the
latter being
the sample
mean of
the sampled
nh/2
units. Then
the replicate
estimator corresponding
to stratum
r is
![]()
![]() The
r-th term
in the
sum of
squares for is
thus:
The
r-th term
in the
sum of
squares for is
thus:
![]()
In stratified random sampling, when a sample of size nr/2 is drawn without replacement from a population of size nr, the sampling variance is
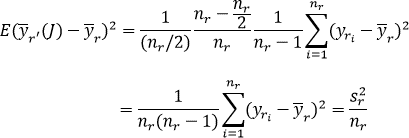
r
![]()
Taking the expectation over all of these stratified samples of size nr/2, it is found that
![]()
In this sense, the jackknife variance estimator “gives back” the sample variance estimator for means and totals as desired under the theory.
In cases where, rather than doubling the weight of one half of one variance stratum and assigning a zero weight to the other, the weight of one unit is multiplied by a replicate factor of (1+δ), while the other is multiplied by (1- δ), the result is that
![]()
In this way, by setting δ equal to the square root of the finite population correction factor, the jackknife variance estimator is able to incorporate a finite population correction factor into the variance estimator.
In practice, variance strata are also grouped to make sure that the number of replicates is not too large (the total number of variance strata is usually 62 for NAEP). The randomization from the original sample distribution guarantees that the sum of squares contributed by each replicate will be close to the target expected value.
For triples, the replicate factors are perturbed to something other than 1.0 for two different replicate factors, rather than just one as in the case of pairs. Again, in the simple case where replicate factors that are less than one are all set to zero, the replicate weights are calculated as follows:
For unit i in variance stratum r
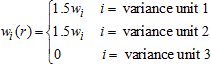
where weight wi is the full sample base weight. Furthermore, for r' = r + 31 (mod 62):

And for all other values r*, other than r and r´,wi(r*) = 1.
![]()
![]()
![]()
![]()
![]() In
the case
of stratified
random sampling,
this formula
reduces to
replacing with for
replicate r,
where is the
sample mean
from a
In
the case
of stratified
random sampling,
this formula
reduces to
replacing with for
replicate r,
where is the
sample mean
from a
![]() “2/3”
sample of
2nr/3
units from
the nr
sample
units in
the replicate
stratum, and
replacing with for
replicate r',
where is the sample
mean from
another overlapping
“2/3” sample
of 2nr/3
units from
the nr
sample units
in the
replicate stratum.
“2/3”
sample of
2nr/3
units from
the nr
sample
units in
the replicate
stratum, and
replacing with for
replicate r',
where is the sample
mean from
another overlapping
“2/3” sample
of 2nr/3
units from
the nr
sample units
in the
replicate stratum.
The r-th and r´-th replicates can be written as:
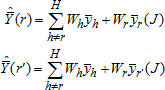
From these formulas, expressions for the r-th and r´-th components of the jackknife variance estimator are obtained (ignoring other sums of squares from other grouped components attached to those replicates):
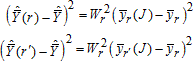
These sums of squares have expectations as follows, using the general formula for sampling variances:
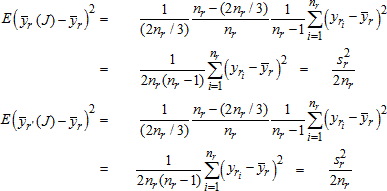
Thus,
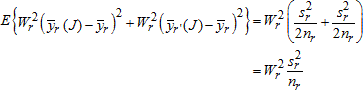
as desired again.

NAEP Technical Documentation Quality Control on Weighting Procedures for the 2018 Assessment
Given the complexity of the weighting procedures utilized in NAEP, a range of quality control (QC) checks was conducted throughout the weighting process to identify potential problems with collected student-level demographic data or with specific weighting procedures. The QC processes included



 checks
performed within each step of the weighting process;
checks performed
across adjacent
steps of
the weighting
process; review
of response, exclusion, and accommodation rates;
checking demographic
data of
individual schools;
checks
performed within each step of the weighting process;
checks performed
across adjacent
steps of
the weighting
process; review
of response, exclusion, and accommodation rates;
checking demographic
data of
individual schools;

 comparisons
with 2014
demographic data;
and nonresponse
bias analyses.
comparisons
with 2014
demographic data;
and nonresponse
bias analyses.
Participation, Exclusion, and Accommodation Rates
Nonresponse Bias Analyses
To validate the weighting process, extensive tabulations of various school and student characteristics at different stages of the process were conducted. The school-level characteristics included in the tabulations were enrollment by race/ethnicity and urbanization classification (four categories based on urban-centric locale). At the student level, the tabulations included race/ethnicity, gender, relative age, students with disability (SD) status, English learners (EL) status, and participation status in National School Lunch Program (NSLP).

NAEP Technical Documentation Final Participation, Exclusion, and Accommodation Rates for the 2018 Assessment
Final participation, exclusion, and accommodation rates were presented in quality control tables for the grade 8 assessments by reporting group. School-level participation rates were calculated as they had been calculated for previous assessments and according to National Center for Education Statistics (NCES) standards.
Grade 8 - Civics
Grade 8 - Geography
School-level participation rates were below 85 percent for public schools in grade 8 civics/geography/U.S. history and for private schools in both grade 8 civics/geography/U.S. history and grade 8 TEL. Student-level participation rates were all above 85 percent. As required by NCES standards, nonresponse bias analyses were conducted on each reporting group falling below the 85 percent participation threshold.
Grade 8 - U.S. History
Grade 8 - Technology and Engineering Literacy (TEL)

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Grade 8 Civics
The following table displays the school-level participation rates and student-level participation, exclusion, and accommodation rates for the grade 8 civics assessment. Various weights were used in the calculation of the rates, as indicated in the column headings of the table.
The participation rates reflect the participation of the original sampled schools only and do not reflect any effect of substitution. The rates weighted by the school base weight and enrollment show the approximate proportion of the student population in the domain that is represented by the responding schools in the sample. These rates differ because schools differ in size.
Participation, exclusion, and accommodation rates for grade 8 civics national assessment, by geographic region and school type: 2018
-
School
School
participation
participation
rates (percent)
rates (percent)
before
before
substitution
substitution
Weighted
Number
(weighted by
(weighted by
Weighted
student
Weighted
of schools
school base
school base
Number of
percent of
participation
percent of
Geographic region
in original
weight
weight
students
students
rates (percent)
students
and school type
sample
and enrollment)
only)
sampled
excluded
after makeups
accommodated
-
School
School
participation
participation
rates (percent)
rates (percent)
before
before
substitution
substitution
Weighted
Number
(weighted by
(weighted by
Weighted
student
Weighted
of schools
school base
school base
Number of
percent of
participation
percent of
Geographic region
in original
weight
weight
students
students
rates (percent)
students
and school type
sample
and enrollment)
only)
sampled
excluded
after makeups
accommodated
National all1 1,130 81.82 73.92 15,500 1.84 92.01 12.45
-
Northeast all
190
90.33
77.75
2,400
2.07
89.11
15.53
Midwest all
220
71.02
71.86
2,500
1.21
92.65
11.42
South all
440
83.97
77.05
6,200
2.32
92.70
14.59
West all
270
81.88
68.41
4,300
1.47
92.57
7.99
National public
790
84.44
85.88
14,000
1.99
91.96
13.04
National private
330
48.66
51.93
1,500
0.05
92.93
5.29
Catholic
80
85.85
89.89
700
0.16
94.64
4.12
Non-Catholic
250
27.28
36.80
800
0.00
90.60
5.91


NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Grade 8 Geography
The following table displays the school-level participation rates and student-level participation, exclusion, and accommodation rates for the grade 8 geography assessment. Various weights were used in the calculation of the rates, as indicated in the column headings of the table.
The participation rates reflect the participation of the original sampled schools only and do not reflect any effect of substitution. The rates weighted by the school base weight and enrollment show the approximate proportion of the student population in the domain that is represented by the responding schools in the sample. These rates differ because schools differ in size.
Participation, exclusion, and accommodation rates for grade 8 geography national assessment, by geographic region and school type: 2018
-
School
School
participation
participation
rates (percent)
rates (percent)
before
before
substitution
substitution
Weighted
Number
(weighted by
(weighted by
Weighted
student
Weighted
of schools
school base
school base
Number of
percent of
participation
percent of
Geographic region
in original
weight
weight
students
students
rates (percent)
students
and school type
sample
and enrollment)
only)
sampled
excluded
after makeups
accommodated
National all1 1,130 81.82 73.92 14,900 1.75 92.03 12.30
-
Northeast all
190
90.33
77.75
2,500
2.42
90.10
15.26
Midwest all
220
71.02
71.86
2,300
1.48
92.88
11.04
South all
440
83.97
77.05
6,100
1.85
92.60
13.59
West all
270
81.88
68.41
3,900
1.38
91.91
9.31
National public
790
84.44
85.88
13,800
1.87
91.95
12.86
National private
330
48.66
51.93
1,100
0.32
93.41
5.02
Catholic
80
85.85
89.89
600
0.00
94.22
3.74
1 National all includes national public, national private, Bureau of Indian Education (BIE), and Department of Defense Education Activity (DoDEA) schools that are located in the United States. School counts are rounded to nearest ten and student counts are rounded to nearest hundred. Detail may not sum to totals because of rounding.
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2018 Geography Assessment.
-
School
School
participation
participation
rates (percent)
rates (percent)
before
before
substitution
substitution
Weighted
Number
(weighted by
(weighted by
Weighted
student
Weighted
of schools
school base
school base
Number of
percent of
participation
percent of
Geographic region
in original
weight
weight
students
students
rates (percent)
students
and school type
sample
and enrollment)
only)
sampled
excluded
after makeups
accommodated

Non-Catholic 250 27.28 36.80 500 0.52 92.08 5.82

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Grade 8 Technology and Engineering Literacy (TEL)
The following table displays the school-level participation rates and student-level participation, exclusion, and accommodation rates for the grade 8 TEL assessment. Various weights were used in the calculation of the rates, as indicated in the column headings of the table.
The participation rates reflect the participation of the original sampled schools only and do not reflect any effect of substitution. The rates weighted by the school base weight and enrollment show the approximate proportion of the student population in the domain that is represented by the responding schools in the sample. These rates differ because schools differ in size.
Participation, exclusion, and accommodation rates for grade 8 TEL national assessment, by geographic region and school type: 2018
-
School
School
participation
participation
rates (percent)
rates (percent)
before
before
substitution
substitution
Weighted
Number
(weighted by
(weighted by
Weighted
student
Weighted
of schools
school base
school base
Number of
percent of
participation
percent of
Geographic region
in original
weight
weight
students
students
rates (percent)
students
and school type
sample
and enrollment)
only)
sampled
excluded
after makeups
accommodated
National all1 760 86.42 68.80 17,500 1.50 93.16 10.84
-
Northeast all
130
89.91
57.05
2,800
2.22
91.41
16.89
Midwest all
140
81.23
75.27
3,200
1.10
93.16
9.53
South all
290
88.51
70.21
7,100
1.42
93.63
11.17
West all
190
85.09
69.14
4,400
1.52
93.67
7.36
National public
620
88.79
85.31
16,100
1.63
93.15
11.48
National private
140
58.38
44.72
1,400
0.00
93.38
3.45
Catholic
30
89.82
87.10
700
0.00
94.54
4.50
Non-Catholic
110
36.19
29.89
700
0.00
91.70
2.71
1 National all includes national public, national private, Bureau of Indian Education (BIE), and Department of Defense Education Activity (DoDEA) schools that are located in the United States. School counts are rounded to nearest ten and student counts are rounded to nearest hundred. Detail may not sum to totals because of rounding.
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2018 TEL Assessment.

NAEP Technical Documentation Participation, Exclusion, and Accommodation Rates for Grade 8 U.S. History
The following table displays the school-level participation rates and student-level participation, exclusion, and accommodation rates for the grade 8 U.S. history assessment. Various weights were used in the calculation of the rates, as indicated in the column headings of the table.
The participation rates reflect the participation of the original sampled schools only and do not reflect any effect of substitution. The rates weighted by the school base weight and enrollment show the approximate proportion of the student population in the domain that is represented by the responding schools in the sample. These rates differ because schools differ in size.
Participation, exclusion, and accommodation rates for grade 8 U.S. history national assessment, by geographic region and school type: 2018
-
School
School
participation
participation
rates (percent)
rates (percent)
before
before
substitution
substitution
Weighted
Number
(weighted by
(weighted by
Weighted
student
Weighted
of schools
school base
school base
Number of
percent of
participation
percent of
Geographic region
in original
weight
weight
students
students
rates (percent)
students
and school type
sample
and enrollment)
only)
sampled
excluded
after makeups
accommodated
National all1 1,130 81.82 73.92 18,800 1.72 92.20 12.05
-
Northeast all
190
90.33
77.75
3,100
1.98
89.60
14.61
Midwest all
220
71.02
71.86
3,000
1.04
92.92
11.13
South all
440
83.97
77.05
7,800
1.71
92.74
13.43
West all
270
81.88
68.41
5,000
2.14
92.75
8.92
National public
790
84.44
85.88
17,400
1.84
92.21
12.51
National private
330
48.66
51.93
1,400
0.19
92.02
6.15
Catholic
80
85.85
89.89
800
0.09
92.60
4.91
Non-Catholic
250
27.28
36.80
600
0.25
91.09
6.93
1 National all includes national public, national private, Bureau of Indian Education (BIE), and Department of Defense Education Activity (DoDEA) schools that are located in the United States. School counts are rounded to nearest ten and student counts are rounded to nearest hundred. Detail may not sum to totals because of rounding.
SOURCE: U.S. Department of Education, Institute of Education Sciences, National Center for Education Statistics, National Assessment of Educational Progress (NAEP), 2018 U.S. History Assessment.

NAEP Technical Documentation Nonresponse Bias Analyses for the 2018 Assessment
NCES Statistical Standards call for a nonresponse bias analysis to be conducted for a sample with a response rate below 85 percent at any stage of sampling. Weighted school response rates for the 2018 assessment indicated that there was a need for school nonresponse bias analyses for public school and private school samples for grade 8. At the student level no nonresponse bias analyses were necessary since the student-level participation rates for all reporting groups were above the 85 percent participation threshold.
Analyses were conducted for the Social Sciences assessments and Technology and Engineering Literacy (TEL) assessment. For the Social Sciences assessments, the analysis was conducted for both public and private schools with Civics, Geography, and U.S. History combined into one analysis because each sampled school was assessed in all subjects. The analysis for the TEL assessment was conducted for private schools only.
The procedures and results from these analyses are summarized briefly below. The analyses conducted consider only certain characteristics of schools and students. They do not directly consider the effects of the nonresponse on student achievement, the primary focus of NAEP. Thus, these analyses are not conclusive of either the existence or absence of nonresponse bias on student achievement.
Each school-level analysis was conducted in three parts. The first part of the analysis looked for potential nonresponse bias that was introduced through school nonresponse. The second part of the analysis examined the remaining potential for nonresponse bias after accounting for the mitigating effects of substitution. The third part of the analysis examined the remaining potential for nonresponse bias after accounting for the mitigating effects of both school substitution and school-level nonresponse weight adjustments. The characteristics examined were census region, private school type, urbanization classification (four categories based on urban-centric locale), size of school (categorical), size of school (continuous), and race/ethnicity enrollment percentages.
Based
on the
school characteristics
available for
the private
school samples,
there does
not appear
to be
evidence of
substantial potential
bias resulting
from school
nonresponse after
substitution and
non-response adjustment.
Please see
the NAEP
2018 Non
Response Bias
Analysis Report![]() for more details.
for more details.

| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Modified | 0000-00-00 |
| File Created | 0000-00-00 |
© 2025 OMB.report | Privacy Policy