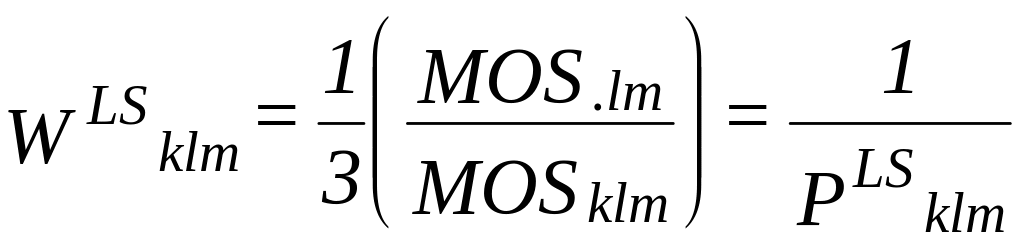Study to Examine Web-base Administration of the Youth Risk Behavior Suvey
Appendix N - Principal Data Collection Detailed Sampling and Weighting Plan.doc
Study to Examine Web-based Administration of the Youth Risk Behavior Survey
Study to Examine Web-base Administration of the Youth Risk Behavior Suvey
OMB: 0920-0763
Appendix N. Principal Data Collection Detailed Sampling and Weighting Plan
Principal Data Collection Detailed Weighting and Sampling Plan
This appendix describes the sampling and weighting plan for the principal data collection. Sampling and weighting procedures are similar to and intentionally modeled after the sampling and weighting plans for the national YRBS. The rationale for developing a sampling and weighting plan comparable to those employed on the national YRBS is that the principal data collection, in effect, seeks counsel from a nationally representative sample of principals in arriving at a decision about the feasibility of transitioning the YRBS from a paper-and-pencil to a Web-based mode of administration. Therefore, the sample of principals to be surveyed should represent a sample of schools comparable to those sampled for the national YRBS. That necessarily includes all efforts on the national YRBS to select schools that will support over-sampling of black and Hispanic students. Because the national YRBS leads ultimately to the selection of a sample of students, we will not mirror the national YRBS sampling and weighting plans fully. However, we will mirror all procedures related to the selection of schools and weighting of data at the school level, especially regarding the over-sampling of schools with high minority concentrations.
The principal data collection will contribute directly to assessing the feasibility of transitioning the YRBS from a paper-and-pencil to a Web-based model of administration. With that in mind, it is essential that the sampling design for the principal data collection mirror the YRBS sampling design as closely as possible so we may obtain feedback from a group of principals who strongly resemble the types of principals we normally would reach through YRBS sampling methods.
Section G.1 describes the sampling methods planned for the selection of primary sampling units (PSUs) and schools for the principal data collection. Section G.2 describes a weighting plan for the principal data collection.
1. Sampling Methods
At the first stage, 225 primary sampling units (PSUs) will be drawn from within 16 strata. Within PSUs, we will select at least three schools with any subset of grades nine through twelve (9-12). Eligible schools include all private and public high schools in the 50 States and the District of Columbia with any of the in-scope grades (9-12). Alternative schools, special education schools, Bureau of Indian Affairs and Department of Defense schools are ineligible, as are vocational education and other schools serving only a “pull-out” population. Forty additional schools will be randomly selected in some already selected PSUs to represent small schools.1 The total number of selected individual schools is expected to be approximately 750 (in the range of 720 to 780).
1.1 Overview
The sampling frame covers 50 States plus the District of Columbia. The YRBS sampling design is a three-stage cluster sampling design stratified by racial/ethnic concentration and MSA status. Within each stratum, a sample of PSUs will be chosen from which a probabilistic selection of schools will subsequently be made. To achieve over-sampling of blacks and Hispanics, the national YRBS normally employs larger sampling rates in high-Hispanic and high-black strata, and a modified measure of size is employed that increases the probability of selection of schools with disproportionately high minority enrollments. For the principal study, we will perform only the first two stages of the usual YRBS sampling process, leading to the selection of a national probability sample of schools.
Data used to build the sampling frame are obtained from Quality Education Data Inc. (QED). QED provides a comprehensive dataset that includes up-to-date telephone verified address and contact information for schools, and incorporates grade-level enrollment and school level minority percentages obtained from NCES Common Core of Data. Frame processing includes computation of size measures, the formation of PSUs and strata, the imputation of missing minority enrollment percentages, and the linking of schools with partial grade ranges.
1.2 Estimation and Justification of Sample Size
We assume an 80% participation rate on the principal data collection, resulting in participation by approximately 600 principals. The sample size of 600 participating principals will be sufficiently large to support estimates with a precision level of 0.05 or better at the 95th confidence interval. This section described the derivation of these sample sizes to achieve the target precision levels.
Design effects, defined as the variance under the actual sampling design divided by the variance that would be attained under a simple random sample of the same size, are expected to be greater than 1.0 for the school sample due to clustering and unequal weighting effects. The anticipated DEFF is between 1.5 and 2.0 as these variance-inflating effects are compensated to some extent by the variance-reducing benefits of stratification.
Table H-1 presents the standard error for estimated proportions based on sample sizes of n=400 and n=600 participants using DEFF=1.6. Table H-1 also shows the confidence interval (half-width) for these scenarios. This table shows that the standard error is at most 2.5 percentage points for n=600 principals, and that the desired confidence levels are achieved (i.e., intervals within +/- 5%) for these sample sizes.
Table 1 Precision Expected for Estimated Percentages Based on Different Sample Size Scenarios: Standard Errors and 95% Confidence Intervals
Standard Errors
School Principal Sample Size (DEFF=1.6)
|
N=400
|
N=600
|
5% |
1.4% |
1.1% |
10% |
1.9% |
1.5% |
15% |
2.3% |
1.8% |
20% |
2.5% |
2.1% |
50% |
3.2% |
2.6% |
Confidence Intervals
School Principal Sample Size (DEFF=1.6)
|
N=400
|
N=600
|
5% |
2.7% |
2.2% |
10% |
3.7% |
3.0% |
15% |
4.4% |
3.6% |
20% |
5.0% |
4.0% |
50% |
6.2% |
5.0% |
1.3 Measure of Size
The proposed sampling approach utilizes PPS sampling methods, in which the probability of a cluster being selected is proportional to the “size” of the cluster. In PPS sampling, a fixed number of units is often selected in the final stage, resulting in an equal probability of selection for all members of the universe. This section describes the proposed measure of size, a measure that will be refined in simulation studies similar to the process used in previous YRBS studies.
One way of accomplishing over-sampling of black and Hispanic students is to use a modified measure of population size during the PPS sample selection steps. A function of the form r h H + r b A + r oO is sought where the r’s are the weighting factors for the Hispanic, black, and Other populations (H, A, and O, respectively). This function increases the chances of schools with relatively large minority enrollments entering the sample. We will use the same weighting function used for the 2007 national YRBS.
The school measure of size is aggregated to compute size measures for PSUs and strata. The weighting function has the effect of increasing the allocation of sample to high‑minority strata and increasing the chances of PSUs with high minority concentrations being included in the sample.
1.4 Definition of Primary Sampling Units
In defining PSUs, several issues are considered:
Each PSU should be large enough to contain the requisite numbers of schools and students by grade (even though we will not actually select students).
Each PSU should be geographically compact so that field staff could go from school to school easily (even though we will not actually visit schools).
There should be recent data available to characterize the PSUs.
PSU definitions should be consistent with secondary sampling unit (school) definitions.
Each PSU should be small enough in terms of the size measure used for sampling that none is selected with certainty.
PSUs consist of counties, groups of smaller adjacent counties, or sub-areas of very large counties. Small population counties are combined in order to include sufficient numbers of schools and students.
Very large counties are sub-divided into smaller units to prevent any PSU from being large enough to be selected with certainty.
PSUs that are large enough to be selected with certainty are split into sub-PSU units. The number of sub-PSU units is computed such that each sub-PSU would be no larger than 80 percent of the original certainty interval. Schools are then sorted by size measure and assigned in rotation to the newly created sub-PSU units.
The county-based PSU definitions were created in 1999 using clustering software developed by the contractor. The software ensures that the PSUs being formed have the correct number of schools and students, while using map data to ensure that the PSUs are compact geographically. The PSU definitions are adjusted each cycle to account for changes in the underlying school population.
1.5 Stratification and Selection of PSUs
This section describes the methods planned for the stratification and selection of the first-stage sample (PSUs), methods that mirror those adopted in the 2005 and 2007 YRBS cycles.
1.5.1 Definition of Strata
The frame PSUs will be organized into 16 strata, based on urban/rural location and minority enrollment. PSUs will be classified as “urban” if they are in one of the 54 largest MSAs in the U.S.; otherwise, they will be classified as “rural”.2 PSUs will be then divided into black and Hispanic groups based on the predominant racial/ethnic minority group.
Four strata will be defined by crossing rural/urban status with black or Hispanic classification. Each of these four strata will be then sub-divided into four sub-strata based on the density of this minority group within the PSU. The cutoffs, or stratum boundaries, for the four density sub-strata will be based on the percentage of the predominant minority within the PSU, with the percentages defining the boundaries computed using an optimization algorithm (Dalenius-Hodges “cumulative square root of f” rule).3
These rules are summarized below.
If the PSU is within one of the 54 largest MSAs in the U.S. it is classified as ‘Urban’, otherwise it is classified as ‘Rural’ (Table 1, column (b)).
If the percentage of Hispanic students in the PSU exceeds the percentage of black students, then the PSU is classified as Hispanic. Otherwise it is classified as black. (Table 1, column (a)).
Hispanic Urban and Hispanic Rural PSUs are classified into four density groupings (Table 1, column (c)) depending upon the percentages of Hispanics in the PSU. (Table 1, column (d)).
Black Urban and black Rural PSUs are also classified into four groupings (Table 1, column (c)) depending upon the percentages of blacks in the PSU (Table 1, column (d)), using bounds given in Table 1.
We note that the PSUs in strata with codes xx1 or xx2 (column (e)) are predominantly non-minority in composition.
Table 2 First-Stage Strata Definition
Predominant
Minority |
Urban/Rural |
Density
Group Number |
Provisional
Bounds |
Stratum
Code |
Black |
Urban |
1 |
0% - 20% |
BU1 |
2 |
20% - 30% |
BU2 |
||
3 |
30% - 56% |
BU3 |
||
4 |
56% - 100% |
BU4 |
||
Rural |
1 |
0% - 16% |
BR1 |
|
2 |
16% - 30% |
BR2 |
||
3 |
30% - 56% |
BR3 |
||
4 |
56% - 100% |
BR4 |
||
Hispanic |
Urban |
1 |
0% - 20% |
HU1 |
2 |
20% - 32% |
HU2 |
||
3 |
32% - 42% |
HU3 |
||
4 |
42% - 100% |
HU4 |
||
Rural |
1 |
0% - 22% |
HR1 |
|
2 |
22% - 44% |
HR2 |
||
3 |
44% - 66% |
HR3 |
||
4 |
66 % - 100% |
HR4 |
The stratum boundaries shown in Table H-2 (column (d)) are from the 2007 cycle, and will be updated using the Dalenius-Hodges algorithm.
1.5.2 Allocation of PSU Sample
The first-stage sample of 225 PSUs will be allocated to the strata using the 2007 YRBS allocation proportionally, i.e., adjusted proportionally for the larger PSU sample sizes.
1.5.3 Selection of PSUs
PSUs will be sampled with probability proportional to size, as follows:
PSUs will be scanned and split, as described in the prior section. Within each stratum, a sampling interval will be computed separately by dividing the sum of the measures of size for the PSUs in the stratum by the number of PSUs to be selected.
Within each stratum, PSUs will be selected using a random start systematic sampling process, with the selection probability proportional to the PSU’s measure of size.
Finally, 40 of the already sampled PSUs will be selected at random to have a small school drawn from it.
1.6 Selection of Schools
The following procedures will be used to select schools in each PSU, the same procedures used in previous YRBS cycles:
The estimated enrollment per eligible grade will be computed for each school by averaging the enrollment at each eligible grade in the school. Minority percentages then will be used to estimate the average number of black, Hispanic and other students per eligible grade. These figures will be combined using the formula given in Section 3.2 to produce the weighted measure of size for each school. Again, even though we plan to select principals and not students, we need to follow YRBS sampling methods related to students in selecting schools.
When grade enrollment is unavailable, the estimated enrollment per eligible grade will be computed by dividing the total school by the total number of grades in the school.
In cases where the minority percentages are not available for a school, they will be imputed using the following sequences of steps:
For private schools, data from the Private School Survey (PSS) will be matched in, where possible, using telephone number and address.
For private schools with no match in the PSS data, overall minority percentages, for the county, computed from PSS data, will be imputed.
For public schools, percentages will be imputed from overall county percentages based on QED data if less than a third of the schools in the county have missing percentages.
Finally, for records not imputed by the above steps, counts of persons between the ages of 15 to 19 years by minority, obtained from US Census 2004 county level estimates, will be used to impute missing minority percentages.
Schools will be divided into two groups based on per grade enrollment.
Large: Estimated enrollment of 25 students or more at each grade.
Small: Estimated enrollment less than 25 students at any grade.
Schools with all four high school grades (9, 10, 11, and 12) will be considered whole schools. A school will be classified as a fragment school if it has any other set of grades. Fragment schools will be combined with other schools (whole or fragment) to form a cluster school that contains all four grades; the cluster school will be treated as a single school during the school draw, with sampling performed at the grade level as described in the next section.
Three large schools will be selected in each sampled PSU with probability proportional to their measures of size. The sampling will be done as follows:
A sampling interval is computed by dividing the sum of the measures of size for large schools in a PSU by three.
Any schools larger in enrollment size than the sampling interval are automatically selected as certainty schools. The sampling interval is recomputed and the process repeated until there are no remaining certainty schools.
The remaining schools are selected using a systematic random sampling procedure.
From each PSU selected for small school sampling, one small school will be drawn with probability proportional to the weighted measure of size, considering only small schools within that PSU.
1.7 Replacement of Schools
We will not replace refusing school schools. However, schools determined to be ineligible will be replaced. Eligibility will be high because the sampling frame largely screens out ineligible schools. However, due to errors and out-of-date information in the frame, some schools will be found to have ceased operation, serve grades other than those of interest, or be a type of school (e.g., alternative or special education) regarded as outside the scope of the national YRBS and, therefore, the principal data collection.
2 Weighting
This section describes to be followed in weighting data resulting from the principal data collection. The process involves several phases of activity that parallel the phases adopted in previous YRBS cycles, including: development of the probability of selection of the student; computation of a basic sampling weight as the inverse of the probability of selection of each school; adjustments for non-response; weight trimming; and, post-stratification adjustments to match (control) population data.
2.1 Probability of Selection
The probability of selection for a school is the product of the probability of selection of the PSU, which is a group of schools, multiplied by the conditional probability of selecting the school.
2.1.1 Probability of Selecting PSUs
I![]()
f
MOSklm is the measure of size for school k in PSU l in
stratum m and if Km is the number of PSUs to be selected
in stratum m, then Pplm is the probability of
selection of PSU l in stratum m:
2.1.2 Probability of Selecting Schools
The probability of selecting large school k in PSU l and stratum m, PLSklm, will be computed as follows:
![]()
2.2 Weight Computations
The sampling weight attached to each school is the inverse of the probability of selection for that school. This basic weight can be adjusted to compensate for non-response, to alleviate excess weight variation, and to match the weighted data to known control totals. A convenient way of computing the basic weight is by inverting the probabilities of selection at each stage, to derive a partial weight or stage weight. The stage weights are then multiplied together to form the overall weight.
2.2.1 School Selection Weight
For large schools, the partial school weight is the inverse of the probability of selection of the school given that the PSU is selected:
2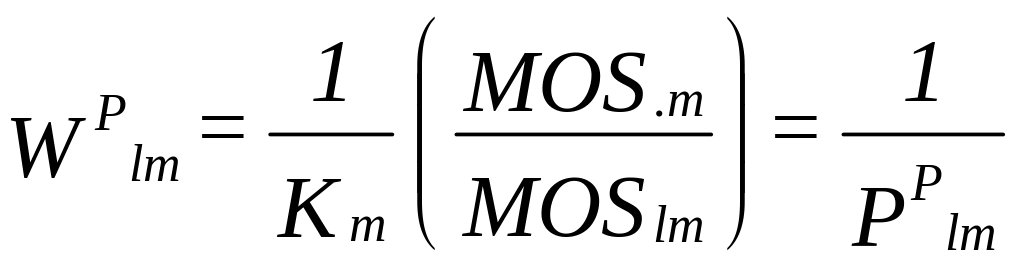
.2.2 PSU
Weights
The weight of the PSU is the inverse of the probability of selection of that PSU:
2.2.3 School Non-response Adjustment
Weights will then be adjusted for school non-participation using strata as weighting classes.
2.3 Weight Trimming
Extreme variation in sampling weights can cause inflated sampling variances, and offset the precision gained from a well-designed sampling plan. One strategy to compensate for this is to trim extreme weights and distribute the trimmed weight among the untrimmed weights in an iterative way.4 During each iteration, an optimal weight, Wo is calculated from the sum of the squared weights in the sample. Then, each weight Wi is marked and trimmed if it exceeds that optimal weight. The trimmed weight is summed within a trimming cell, and spread out proportionally over the unmarked cases in the cell. This process is repeated until little or no weight is being trimmed.
2.4 Post-stratification to National Estimates of Student Enrollment Distribution
Post-stratification methods use known population (or control) totals or percentages. We will use national data available from the National Center for Education Statistics (NCES): a) for private schools, data from the Private School Universe Survey (PSS), and b) for public schools, data from the Common Core of Data (CCD). School-level data will be used for post-stratification by school type (private versus public) and by Census region. We will also consider post-stratification by school size using median school enrollments computed separately for private and public schools.
1 Small schools are defined as schools in which any high school grade present in the school contains less than 25 students.
2 The largest 54 MSA contain roughly 50% of the U.S. population.
3 Cochran, W.G. (1977) Sampling Techniques. J. Wiley, New York.
4 Potter F. “A Study of Procedures to Identify and Trim Extreme Sampling Weights,” in Proceedings of the Section on Survey Research Methods of the American Statistical Association, pp 225-230, 1990.
| File Type | application/msword |
| Author | kflint |
| Last Modified By | arp5 |
| File Modified | 2007-09-17 |
| File Created | 2007-09-17 |
© 2026 OMB.report | Privacy Policy