1205-0441 Justification Part Bdoc
1205-0441 Justification Part Bdoc.doc
Evaluation of the Individual Training Account Experiment
OMB: 1205-0441

The Evaluation of Individual Training Account Experiment: OMB Supporting Statement, Part B
Irma Perez-Johnson
Patricia Nemeth
Kenneth Fortson
Quinn Moore
Submitted to:
U.S. Department of Labor Employment and Training Administration 200 Constitution Ave., NW Room N-5637 Washington, DC 20210
Project Officer:
|
Submitted by:
Mathematica Policy Research, Inc. P.O. Box 2393 Princeton, NJ 08543-2393 Telephone: (609) 799-3535 Facsimile: (609) 799-0005
Project Director: |
CONTENTS
Page
b. collections of information involving statistical
methods 1
1. Respondent Universe and Sampling 1
2. Statistical Methodology, Estimation, and Degree of Accuracy 5
3. Methods to Maximize Response Rates and Data Reliability 14
4. Tests of Procedures or Methods 21
5. Individuals Consulted on Statistical Methods 22
REFERENCES 23
SUPPORTING STATEMENT, PART B: COLLECTIONS OF INFORMATION INVOLVING STATISTICAL METHODS
1. Respondent Universe and Sampling
For the second follow-up survey of the Extension of the Evaluation of the Individual Training Account (ITA) Experiment (hereafter referred to as ITA2), we plan to attempt an interview with all of the original sample members from the first follow-up survey. The ITA2 survey is a modification of the original ITA survey, which was approved by OMB (approval number 1205-0441).
The respondent universe is individuals in the eight study sites who were randomly assigned to one of the three ITA approaches during the study intake period.1 The size of the universe depended on the flow of customers deemed eligible for training. Approximately 8,000 people were randomly assigned during the study intake period. The table below provides the number of ITA customers who were enrolled in each study site and overall:
Study Site (State) |
Sample Size |
Atlanta Regional Commission (GA) Northeast Georgia Regional Development Center (GA) |
1,408 171 |
The Workplace, Inc. (CT) |
1,033 |
Charlotte-Mecklenburg Workforce Development Board (NC) |
1,401 |
First Coast Development, Inc. (FL) |
779 |
The Workforce Board of Northern Cook County (IL) |
1,807 |
City of Phoenix Human Services Department (AZ) |
646 |
Maricopa County Human Services Department (AZ) |
673 |
Total |
7,918 |
The survey sample for the first follow-up survey included a randomly selected sample of 4,800 study participants. The ITA2 follow-up survey will include all of the 4,800 sample members from the first follow-up survey, regardless of whether or not they responded during the first round. These 4,800 survey participants were randomly selected from the 7,918 individuals who were randomly assigned to the ITA approaches.
Because we needed to draw the survey sample and begin interviewing before intake into the ITA Experiment was completed, the sampling occurred in two steps.2 The samples selected at each step were independent of each other. In the first step, 4,040 customers were randomly selected from among customers who had been randomly assigned before July 2003. In the second step, an additional sample of 760 customers was randomly selected from among customers who were randomly assigned in July 2003 or later.
A stochastic allocation procedure was used to ensure that the sampling rate was the same across all study sites at each of the two steps. Specifically, at each step of sampling, we stratified the ITA study participants by site. Then we used “probability minimum replacement” techniques (also known as Chromy’s procedure) to allocate the sample to each stratum so as to preserve equal probabilities of selection and maintain a fixed overall sample size. In the first step of sampling, we sampled to achieve a uniform rate of 62.9 percent, making each site’s share of the follow-up survey sample proportional to its share of the overall ITA study population. In the second step, we adjusted the sampling rate (to 50.8 percent) to ensure that we would select a total of 4,800 ITA study participants for the follow-up survey sample. The sampling rate was lower in the second step because, in the six study sites that were still enrolling ITA study participants, more people than projected were found eligible for an ITA after July 2003. Two study sites had discontinued intake into the ITA Experiment before July 2003 and, hence, had no additional ITA study participants selected for the survey sample in the second step of sampling.
The first ITA follow-up survey achieved a response rate of 82 percent. Several factors contributed to the high response rate for that survey, including the salience of the survey’s topic for prospective respondents, sample members’ receipt of an ITA training voucher, and our close adherence to best practices in survey research.
For the ITA2 follow-up survey, we expect a 70 percent response rate. This expectation is based principally on the length of time that has passed since the first survey was conducted. Even though we will continue to adhere to best practices in survey research (e.g., sending informative advance letters to sample members, intensive locating efforts, extensive interviewer training, utilization of calling strategies that maximize the probability of contact, refusal-conversion procedures, etc.), the length of time lapsed since last contact with the sample members presents several challenges for the second-wave data collection effort. For the ITA2 survey, the available contact information is likely to be out-of-date for more respondents, making contact more challenging. Also, the survey topic is less salient to sample members since approximately five to seven years have passed since the time of random assignment and their participation in the ITA Experiment.
The first ITA follow-up survey was conducted approximately 15 months after random assignment, when enrollment in the ITA study and receipt of the ITA voucher were still prominent in sample members’ minds. Offering a monetary payment for survey participation was deemed unnecessary since all ITA study participants were offered a voucher for financial assistance with training. The offer of the ITA voucher was expected to serve the same function as a response incentive—namely to make the study salient, to highlight its importance, and to activate the social-psychological principles of cooperation, motivation, and reciprocation that encourage survey participation (Groves et al. 2004). Following best practices in survey research, first follow-up contacts with sample members began 15 months after random assignment. Hence, the available contact information was relatively up-to-date and highly likely to be accurate, increasing the probability of successful contact with sample members.
In contrast, the ITA2 follow-up survey will be conducted between four and six years after the sample member’s previous interview (depending on when individuals completed their first follow-up interview). For nonrespondents from the first follow-up survey, the most recent contact information available is from a baseline information form (BIF), which participants completed before random assignment. Contact information for our sample in this ITA2 follow-up survey is therefore between four and eight years old.
Substantial time has also passed since sample members were offered and/or received their ITA training vouchers. (Some ITA study participants opted out of ITA-funded training.) For this reason, we anticipate greater difficulties in making the survey topic salient, eliciting respondents’ cooperation, and minimizing sample attrition.
For these reasons, we regard an overall response rate of 70 percent as a reasonably ambitious target for the ITA2 follow-up survey. The proposed 70 percent response rate for the ITA2 follow-up survey sets a very high expectation of success with contacting and gaining cooperation with first follow-up survey respondents. Given the 82 percent response rate for the first follow-up survey (i.e., 3,933 out of 4,800 sample members completed the survey), an overall response rate of 70 percent (i.e., 3,360 respondents) for the ITA2 follow-up survey is equivalent to an 85 percent response rate from the first follow-up survey respondents.
The proposed 70 percent response rate is still vital to ensuring our ability to generate reliable and unbiased estimates of the effects of the ITA approaches on various participant outcomes. High response rates are often considered a good indicator of data quality (as measured by sample representativeness). Yet, nonresponse bias analyses have found contradictory evidence on the effects of response rates on study estimates (Groves 2006; Groves et al. 2006). Some studies have shown the marginal gains in response rate to be important in achieving unbiased estimates, while others find that they result in no impact on estimates (Stapulonis, Kovak, and Fraker 1999) or that including the most reluctant respondents can contribute to bias in estimates for certain statistics (Olson 2006). Moreover, the influence of the response rate may vary for different study estimates, yet it is difficult to predict a priori which estimates will be influenced more strongly or more weakly (Groves 2006; Groves et al. 2006). A nonresponse bias analysis is therefore essential to understand the limits of uncertainty in the survey data collected.
MPR will conduct nonresponse bias analyses, using data from both the first-wave participant survey and administrative records data to evaluate the representativeness of the ITA2 follow-up survey data. The results of these analyses will be used to create weights that adjust for survey nonresponse, and these weights will be applied in our analyses of the ITA2 survey data (as was done in analyses of the first ITA follow-up survey data). We discuss our plans for nonresponse bias analysis further in Section B.3.b.
2. Statistical Methodology, Estimation, and Degree of Accuracy
The primary objective of the evaluation of the ITA Experiment and its extension is to provide statistically valid and reliable estimates of the relative effects of the three ITA approaches on key outcomes, including participation in training, employment and earnings, and participation in government support programs. Use of a classical experimental design, in which applicants were assigned randomly to the three approaches, ensures that measured impacts represent valid estimates of the relative effects of the approaches. The measured impacts are internally valid for the eight study sites. Since these study sites were chosen purposively, the results cannot be generalized to a wider population with a known degree of statistical precision.
For the ITA2 evaluation, impacts will be estimated in the same way as in the original study—that is, by computing differences in mean outcomes between pairs of ITA approaches, adjusted for random differences at intake using multivariate regression. Regression adjustments will increase the precision of the impact estimates.
Given this design, the main question is whether the impact estimates will be precise enough to detect likely impacts. To answer that question, Table 3 shows minimum detectable impacts for comparisons between two ITA approaches for quarterly earnings and dichotomous outcomes like participation in training. The analysis was done for a pooled analysis for the entire sample using the ITA survey sample of 4,800 and the administrative data sample of 8,000. We also show minimum detectable impacts for the average site and for subgroups over all sites that contain half of the sample and one-third of the sample.
TABLE 3
MINIMUM
DETECTABLE DIFFERENCES BETWEEN ITA APPROACHES
|
|
Minimum Detectable Impacts |
|
Sample |
Available Sample |
Dichotomous Outcomes |
Quarterly Earnings (dollars) |
Survey Sample (4,800) |
|
|
|
Full sample |
1,120/1,120 |
.053 |
132 |
Half sample |
560/560 |
.075 |
187 |
One-third sample |
373/373 |
.092 |
229 |
Average site sample |
140/140 |
.150 |
374 |
Administrative records (8,000) |
|
|
|
Full Sample |
2,666/2,666 |
.034 |
86 |
Half sample |
1,333/1,333 |
.048 |
121 |
One-third sample |
889/889 |
.059 |
148 |
Average site sample |
333/333 |
.097 |
242 |
Note: The calculations assume (1) a 95 percent confidence level with an 80 percent level of power; (2) a two-tail test; (3) a reduction in the variance of 20 percent owing to the use of regression models; (4) a 70 percent response rate for the ITA2 interview (and 100 percent for the administrative records); and (5) a standard deviation of .5 for dichotomous variables and $1,250 for quarterly earnings, which reflect findings from the original evaluation (McConnell et al., 2006). The minimum detectable differences (MDD) are calculated using the following formula:
![]() where
= 2.8 for a two-tail test,
is the standard deviation of the variable,
where
= 2.8 for a two-tail test,
is the standard deviation of the variable,
R2
is the variance
explained by the regression model, r is the response rate, and n is
the size of each ITA model group.
Experiences in the initial evaluation of the ITA Experiment confirmed that sample sizes for the survey sample and the administrative sample were large enough to detect differential impacts among the three ITA approaches both for key dichotomous and continuous variables. The initial evaluation found differences in the use of counseling and approval of training, in the amounts of UI benefits received, and in the number of weeks spent in training that easily exceed the minimum detectable differences shown in Table 3 for the full sample and for major subgroups, for both the survey and administrative samples (McConnell et al., 2006). Based on the first ITA survey, the evaluation also estimated a statistically significant difference in average quarterly earnings of $262 between Approach 1 and Approach 3 (ibid.). This difference is more than double the MDE ($124) in quarterly earnings computed for the first ITA follow-up survey.3 Similar to the original study, the ITA2 study should be able to detect differences in quarterly earnings of around $132 with an 80 percent level of power, and smaller differences with lower levels of power.
The following discussion provides additional details on ITA2 estimation procedures, which are largely the same procedures used for the original evaluation.
Estimating Overall Impacts. Random assignment will allow us to assess the relative effectiveness of the ITA approaches by comparing average outcomes across the approaches. Because all of the approaches offered ITAs to customers, there is no control group that was denied services. Hence, comparing outcomes for two approaches allows us to assess the difference in the impacts of one ITA approach versus another, not the effects of a being offered an ITA versus not being offered an ITA. Note also that the impact analysis will assess the impacts of the various ITA “offers,” not the impacts of the training received, as some persons in each approach chose not to enroll in ITA-funded training. The impacts of the offer may also reflect the impacts of related assistance, such as counseling, in addition to the direct impacts of ITA-funded training.
Because customers were randomly assigned to the three approaches, a simple comparison of the average outcome measures in two approaches provides an unbiased estimate of the effect of one approach versus another. As in the original evaluation, we plan to estimate the effects of the ITA approaches using a regression model, both to increase precision and to adjust for chance differences in the characteristics of customers randomly assigned to the three approaches.4
O![]()
ur
estimates of the relative effects of the three approaches will be
based on a comparison of customers randomly assigned to one of the
three approaches with customers randomly assigned to another
approach. To compute the relative effects of the three approaches, we
will estimate a statistical model that predicts the outcome of
interest as a function of approach, site, and a set of background
characteristics. The basic form of this model is:
where:
ysi is the outcome of interest for customer i in site s
Ssi equals 1 if customer i was in site s and 0 if not
A1si equals 1 if customer i in site s was in Approach 1 and 0 if not
A3si equals 1 if customer i in site s was in Approach 3 and 0 if not
Csi is a vector of baseline characteristics of customer i in site s
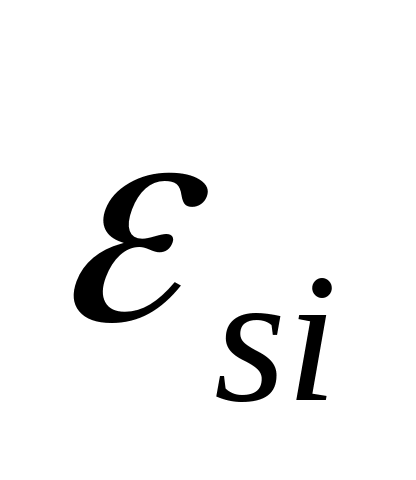 is a random error term that captures the effects of unobserved
factors that influence the outcome. It is assumed to have a mean of
zero conditional on {A}, {C}, and {S}.
is a random error term that captures the effects of unobserved
factors that influence the outcome. It is assumed to have a mean of
zero conditional on {A}, {C}, and {S}.
The
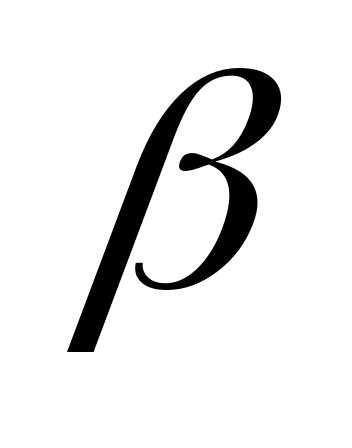 and
and
 terms are parameters or vectors of parameters to be estimated.
terms are parameters or vectors of parameters to be estimated.
The parameters of
greatest interest are
![]() and
and
![]() because
they show the effect on customers of being in Approach 1 (or 3) in
site s, relative to being in Approach 2. These parameters can
thus be interpreted as the causal effect of being assigned to
Approach 1 (or 3) rather than being assigned to Approach 2, in site
s. The
because
they show the effect on customers of being in Approach 1 (or 3) in
site s, relative to being in Approach 2. These parameters can
thus be interpreted as the causal effect of being assigned to
Approach 1 (or 3) rather than being assigned to Approach 2, in site
s. The
![]() and
and
![]() terms provide the estimates of the relative effects of Approach 1 (or
3) versus Approach 2 within each site. The relative effect of
Approach 1 versus Approach 3 in site s is obtained by
computing
terms provide the estimates of the relative effects of Approach 1 (or
3) versus Approach 2 within each site. The relative effect of
Approach 1 versus Approach 3 in site s is obtained by
computing
![]() .
Thus, within each site (s=1 to 8) we will obtain three effect
estimates:
.
Thus, within each site (s=1 to 8) we will obtain three effect
estimates:
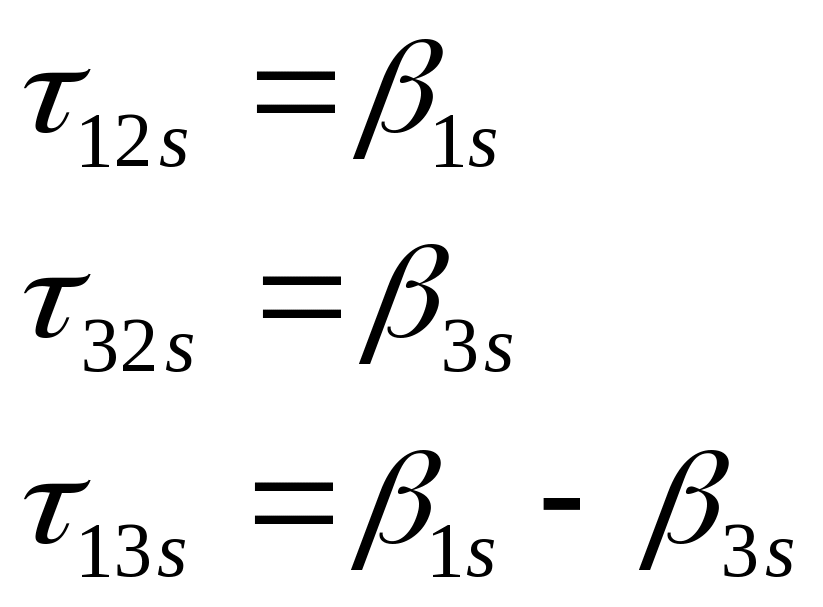
To obtain the average effect across all sites, we will compute a weighted average of the effects in each site, where the site effects are weighted by the proportion of customers in each site:
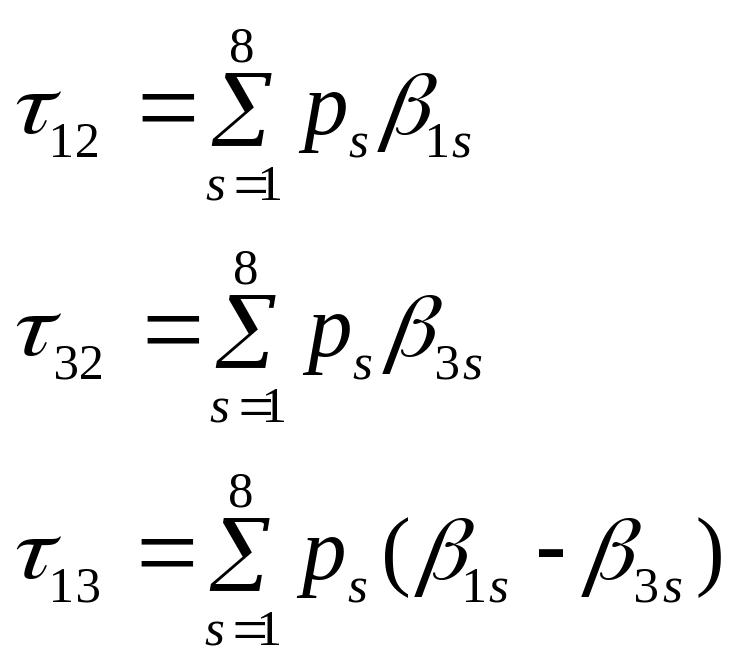
Similar formulas will be used to test whether the effect within each site is different from the effect in the other sites.
The site weights used in the above formulas are the proportion of customers in each site. This is equivalent to pooling all customers across sites and weighting each customer equally, regardless of their site of origin. Our rationale for pooling across sites is based on three factors: (1) all sites were asked to implement the same three approaches; (2) the implementation of the three ITA approaches was similar across our study sites; and (3) while the contextual factors do vary across the sites, we saw them as having had a limited influence on the outcomes of ITA study participants by approach. We will examine and report results separately by site and, as a sensitivity analysis, examine whether results differ when sites are weighted equally.
For continuous
outcomes, we plan to estimate regression parameters using ordinary
least squares, as done in numerous studies such as Dale and Krueger
(2002) and Kling (2006). Regression parameters for binary outcomes
will be estimated using logistic regression, which models the “log
odds of success” as a linear function of the predictors:
![]() ,
where
,
where
![]() .
As in the original evaluation, regression models will be weighted to
account for the sampling design and unit nonresponse (discussed
further in section B.3).
.
As in the original evaluation, regression models will be weighted to
account for the sampling design and unit nonresponse (discussed
further in section B.3).
The explanatory variables (i.e., the variables represented by the vector C in the equation above) included in the regression model will be demographics (age, sex, race/ethnicity), marital status, has children (yes or no), education level (associate’s degree, bachelor’s degree or higher), vocational certification, primary language (English or not), type of worker (dislocated or adult), and baseline employment characteristics (employed at baseline, earnings in 12 months prior to baseline). In the original evaluation, these variables were selected using preliminary investigation of variables predictive of outcomes using a stepwise variable-selection procedure (as recommended in Neter et al., 1996), as well as substantive knowledge.
E![]()
stimating
Subgroup Effects. As in the original study, we will use a slight
simplification of the main model when estimating effects for
subgroups of customers, such as dislocated workers or adult workers.
In particular, the model will not include indicators for site when
estimating subgroup effects. Including the site indicators and
interactions with the subgroup indicator would greatly increase the
number of parameters in the model and may result in less precise
estimation of the overall subgroup effects. As a result, excluding
these variables will allow efficient estimation of the overall effect
across all sites for each subgroup, which are the parameters of key
interest in the subgroup analysis. The model used for subgroups is
thus:
where the variables are defined as above, and
![]() if customer i is in group G and equals 0 otherwise. The
relative effects for subgroup G are calculated as:
if customer i is in group G and equals 0 otherwise. The
relative effects for subgroup G are calculated as:

Similarly, the effects for customers not in subgroup G (G=0) are:
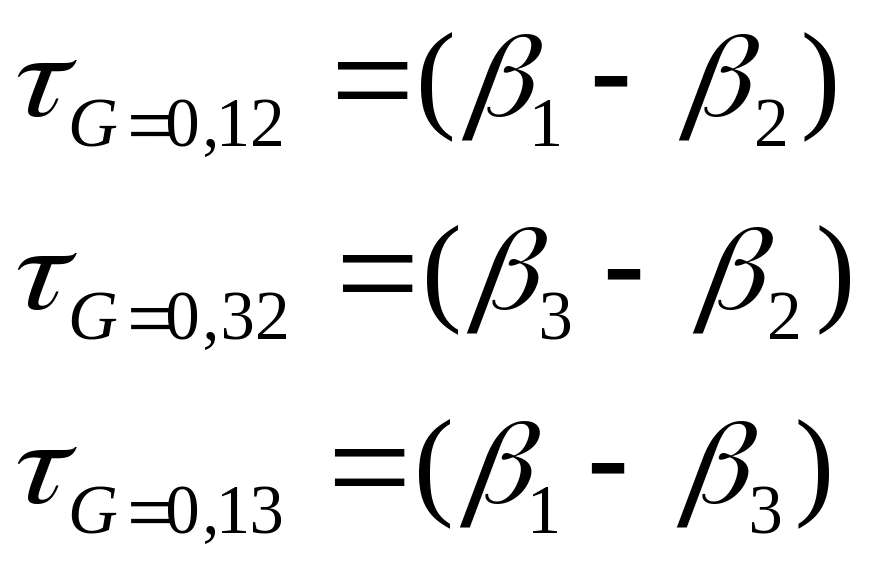
Tests of whether the effects are different for customers in and not in subgroup G can also be done, using similar combinations of the coefficients. When sites are weighted by their size, as in the main analyses, the results obtained using this model are equivalent to the overall effects (averaged across sites) obtained using the model presented earlier.
The subgroups for which we plan to estimate the relative effects of the three approaches are based on:
Customer type: Dislocated workers and adult workers
Education: Customers with at most a high school degree, and customers with more than a high school degree
Vocational certificate: Customers with or without a vocational certification at the time of random assignment
Age: Customers over age 40 and customers under age 40
Sex: Female customers and male customers
Race/ethnicity: Nonminority customers (white non-Hispanic) and minority (black, Hispanic, Asian, other) customers
Training status: In training at or just before random assignment, and not in training at or just before random assignment
Calculating Standard Errors. To determine whether effect estimates are statistically significant, we will compute standard errors that account for the study’s sample design and for the clustering of customers within sites. For outcomes based on data from the survey, we will use regression procedures designed for complex survey data that calculate correct standard errors given the sampling and nonresponse weights (described in B.3) and the stratification by site (Brogan 1998). For outcomes based on the full population of customers—such as those based on data from the UI wage records or the STS—we will use the same procedures, but we will not use weights, since we will not need to account for survey sampling or survey nonresponse.
The calculation of standard errors will reflect the fact that the ITA sites were chosen purposively, not randomly. Because sites had to be willing and had to apply to participate in the experiment, it was impossible to select a nationally-representative set of sites. Therefore, the results generalize only to the set of sites in this study, and not to a broader population of workforce development agencies.
For the exact formulation of the standard errors of the linear regression model, it is helpful to first rewrite the regression equation in matrix notation as:
![]() ,
,
where y is the (n x 1) vector of outcomes
for each of n respondents; X is the (n x k) matrix of the k
independent variables for each of the n respondents; and
![]() is the (n x 1) vector of residuals. The (k x 1) estimator
is the (n x 1) vector of residuals. The (k x 1) estimator
![]() is then:
is then:
![]() ,
,
where W is the (n x n) diagonal matrix of
weights, with diagonal element wsi for
customer i in site s. With this formulation, the
variance-covariance matrix for
![]() can be expressed as:
can be expressed as:
![]() .
.
The inner term
![]() is somewhat complicated. We begin by rewriting the matrix X as
stacked (k x 1) vectors:
is somewhat complicated. We begin by rewriting the matrix X as
stacked (k x 1) vectors:
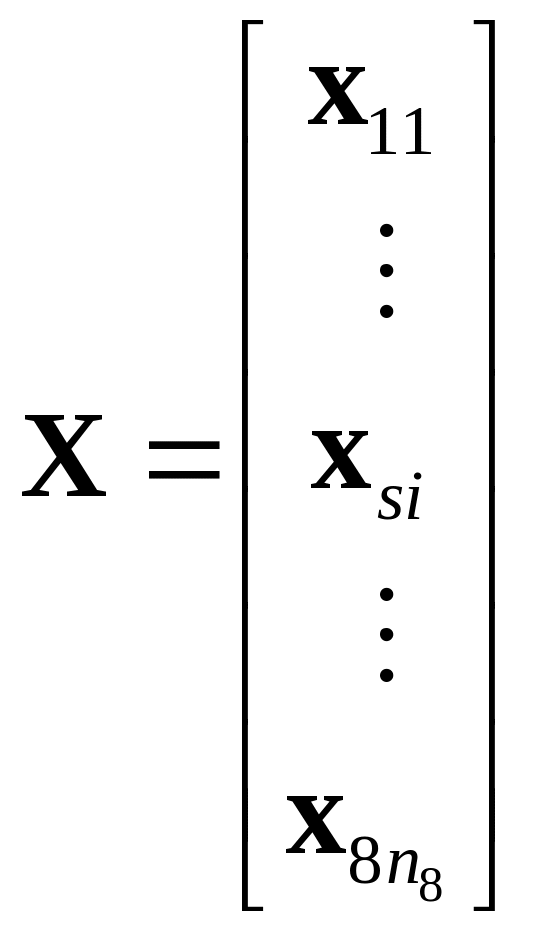 ,
,
where xsi is
the covariate vector for customer i in site s. We also
define esi to be the estimated residual for
customer i in site s. The (k x k) matrix
![]() can then be written as:
can then be written as:
![]() ,
,
where
![]() represents the average of this term for site s, and ns
is the number of customers in the sample for site s.
Intuitively,
represents the average of this term for site s, and ns
is the number of customers in the sample for site s.
Intuitively,
![]() amounts to a more complicated version of the common Huber-White
estimator with probability weights, adjusted to eliminate
between-site variability.
amounts to a more complicated version of the common Huber-White
estimator with probability weights, adjusted to eliminate
between-site variability.
Using the variance and covariance elements of
![]() together
with the site proportions ps, we can then
characterize the variance of the pooled impact estimate as:
together
with the site proportions ps, we can then
characterize the variance of the pooled impact estimate as:
![]() .
.
3. Methods to Maximize Response Rates and Data Reliability
a. Response Rates
As discussed in B.1, for the ITA2 survey, we expect a response rate of 70 percent, which is based on our experiences with the original ITA survey (McConnell et al., 2006) and adjustments for the length of time lapsed since the first survey was conducted. In addition to the offer of an incentive payment, we plan to use several other strategies to achieve a high response rate.
First, before interviewing begins, an advance letter describing the purpose and sponsorship of the survey will be mailed to ITA study participants who are in the survey sample. This advance letter will assure sample members that the caller is conducting a research interview and not soliciting donations or selling anything. Letters will be sent approximately one week before the sample is released to the computer-assisted telephone interview (CATI) call scheduler. The letter will request up-to-date contact information and provide a toll-free call-in number.
Second, staff from MPR’s experienced pool of interviewers will be recruited and extensively trained. These interviewers will be thoroughly trained on data collection procedures, including methods for promoting cooperation among sample members. Interviewers especially skilled at encouraging cooperation will be available to persuade reluctant respondents to participate and will be assigned to attempt conversions with respondents who initially refuse (except for hostile refusals). Bilingual interviewers will also be available for conducting interviews in Spanish.
Third, call scheduling will allow respondents to select the time most convenient for them to be interviewed. We plan to conduct this survey using CATI, which ensures control of sample releases, call scheduling, and questionnaire logic and completeness.
Fourth, we will make extensive use of various on-line databases to try to locate sample members who have moved. Finally, in-person field staff will be used to locate sample members without a known address or telephone number. We expect these techniques to yield a 70 percent response rate. We expect that 60 percent will be achieved with the telephone survey effort and the remaining 10 percent will result from the in-person field effort. These estimates are based on MPR's results from the first follow-up survey, as well as survey results from similar projects in which the in-person field locating and interviewing efforts yielded a 10 to 15 percent higher response rate.
b. Reliability of Data Collection
The draft questionnaire for the ITA2 follow-up survey was based extensively on the questionnaire for the first follow-up survey (OMB number 1205-0441), which in turn was based extensively on questionnaires developed for other U.S. Department of Labor studies, including the Trade Adjustment Assistance Survey (OMB number 1205-0306); the Job Search Assistance Experiment Survey (OMB number 1205-0367), and the National Job Corps Study Thirty-Month Follow-Up Interview (OMB number 1205-0360). The questions were designed to ensure that they would be easily understood by respondents and were revised based on an internal review, a review by DOL, and a pretest.
Our goal for the ITA2 follow-up questionnaire was to keep it as similar as possible to the original ITA follow-up questionnaire to maintain comparability of the data collected with these survey instruments. Since approximately five years will have passed since the last survey and up to eight years will have passed since random assignment, the survey questionnaire had to be updated to reflect changes in the reference periods and the fact that respondents would likely be unable to recall reliably some types of information.
Thus, changes to the instrument primarily involved recall aids (reminding respondents of their last jobs or education and training programs), changing reference periods for income sources (from the time since random assignment to the last 12 months), and deleting questions that could not be answered reliably so long after service receipt, such as satisfaction with one-stop services received around the time of random assignment. We also included new response options that respondents had previously provided as “other/specify” responses. The addition of these response categories helps respondents to answer about their experiences accurately. To facilitate the recording of answers, we updated the response options available to interviewers when coding open-ended responses. These changes do not affect what respondents hear but simply how interviewers record responses (and are noted in yellow in the revised questionnaire document).
The use of CATI to conduct the survey also helps ensure the reliability of the data. It controls question branching (reducing item nonresponse due to interviewer error), modifies wording (providing memory aids and probes and personalizing questions), and constructs complex sequences that are not possible to produce or are less accurate in hard copy surveys. The probes, verifications, and consistency checks are built into the system’s standardized procedures. These procedures ensure the reliability of the data collection methods and the data collected through those methods.
MPR will monitor 10 percent of each interviewer’s work using silent call-monitoring equipment and video monitors that display the interviewer’s screen. Supervisors evaluate interviewer performance based in part on this monitoring. Supervisors then discuss these evaluations and coach interviewers in order to maintain high quality data.
c. Adjusting for Survey Sampling, Survey Nonresponse, and Item Nonresponse
When the ITA2 survey is completed, we will conduct an analysis of nonresponse to assess whether the survey sample is representative of the initial population of ITA applicants. In particular we will examine whether any differences in response rates among individuals assigned to each ITA approach may affect the findings. This analysis will use background data collected on the MIS including demographic data. Sample weights will be assigned to adjust for differences between respondents and nonrespondents in important background characteristics.
Developing analytical weights. For analyses based on the survey, respondents will be assigned weights to be used in estimating the effects of the ITA approaches. This weighting will have two purposes in addition to adjusting for nonresponse. First, after the first ITA participant follow-up survey, we constructed weights that remove the effects of the different sampling rates before and after July 2003, so that customers are represented equally irrespective of when they were randomly assigned. Second, weights will be constructed so that the weighted total number of survey respondents equals the total number of customers in the ITA Experiment.
Baseline weights. To adjust for the differential sampling rate in the first and second stage of the selection of the survey sample, we assigned a sampling weight of:
![]()
Thus, for customers who were selected for the survey sample in
Stage 1, the baseline weight is
![]() ,
while customers selected in the second stage have baseline weight
,
while customers selected in the second stage have baseline weight
![]() .
This baseline weight is the inverse of the customer’s
probability of selection for the survey sample. Because of the
stochastic allocation procedure used to select customers, the
probability of selection is the same for customers in all sites
within each stage.
.
This baseline weight is the inverse of the customer’s
probability of selection for the survey sample. Because of the
stochastic allocation procedure used to select customers, the
probability of selection is the same for customers in all sites
within each stage.
Survey nonresponse weights. Nonresponse weights will be constructed to adjust for differences in characteristics between respondents and nonrespondents. Using information from the baseline information form completed by all customers, as well as from UI wage records data available from all customers, we will compare the characteristics of survey respondents and nonrespondents, separately by site. The construction of these weights will involve grouping survey respondents into cells based on variables or characteristics related to their probability of responding to the survey by study site.5
The nonresponse weights will be constructed to adjust for differences in these characteristics between respondents and nonrespondents. For each cell, the nonresponse adjustment is calculated by dividing the sum of the number of respondents and nonrespondents by the number of respondents in the cell.
![]()
Ensuring that weights sum up to the population total. To compute final survey weights, the preliminary weights will be ratio-adjusted to ensure that, within strata defined by site, approach, and dislocated/adult worker status, the final weights add up to the population total. The following adjustment will be made to each customer’s weight:
![]()
Final weights. The final weight, a combination of the sampling weight, the nonresponse adjustment, and the post-stratification adjustment would thus be calculated as:
![]()
Imputing Values for Item Nonresponse. For the ITA2 survey, we expect to use the same procedures to handle item nonresponse as in the original ITA participant follow-up survey, which had very little missing data on the survey as a whole.6 For outcomes with missing data, we would omit the sample member in the analysis of that outcome. For covariates, we imputed values based on the mean of the observed data (for continuous covariates) or the most common value (for categorical variables). For the race/ethnicity variables, we included nonrespondents in the “other” race category.
For missing data items used in the construction of employment, earnings, and training outcomes, we used a hot-deck imputation procedure to impute missing “building block” data items rather than omitting the sample member with missing data from the analysis.7 We imputed the “building block” data items rather than the composite outcome variables because this made use of all the information we had available. As in the original survey, we will implement checks—of both building block and composite outcome variables—to ensure that imputations are reasonable. We will also assess the sensitivity of our impact estimates to the use of imputed versus only observed data.
d. Nonresponse Bias Analysis
As in any survey, some sample members in the ITA2 follow-up survey will not be located and others will not be able or willing to respond to the telephone survey. For other individuals, the relevance of the study will have diminished substantially by the time of data collection. Thus, the ITA2 follow-up survey has the added burden of the length of time since participation in the ITA Experiment. As noted previously, we achieved an 82 percent response rate for the first follow-up survey and expect a 70 percent response rate for this second follow-up. The lower response rate increases the potential for nonresponse bias, but does not imply that survey estimates will necessarily exhibit bias.
The purpose of the nonresponse bias analysis is to provide some indication of whether a possible nonresponse bias does exist, an indication of the data items and populations for which survey estimates may have a greater potential for bias, and the possible extent of nonresponse bias in survey estimates. However, because survey data will not be available for nonrespondents, we can never be certain if bias does or does not exist in the survey estimates.
For the nonresponse bias analysis, we will use the various data collected in this study. These include data from the study MIS and other administrative records (including demographic information and information about employment and training services received as part of the experiment), UI wage records (including employment status and quarterly earnings), and the first follow-up survey (including information on the receipt of, and satisfaction with, services and training). Because the administrative data and UI wage records will be available for all ITA study participants, they will be the most useful data to define the subgroups for the nonresponse analysis
For the nonresponse bias analysis, we plan the following steps:
i. Compute response rates for key subgroups of ITA study participants for “baseline” characteristics based on the administrative and wage records data.
ii. Compare the weighted distributions of respondents and nonrespondents for baseline characteristics.
iii. Identify the characteristics that best help predict nonresponse through a CHAID analysis and logistic regression modeling, and use this information to generate nonresponse weight adjustments.
iv. Compare the distributions of respondents using the fully response-adjusted analysis weights for baseline characteristics to the distributions for the full sample comparably weighted using the unadjusted sampling weights.
These analyses will be conducted within and across sites to assess whether the potential for nonresponse bias differs across sites. Below, we discuss each of these steps in greater detail.
Compute response rates for subgroups
The response rate for the subgroups will be computed using the AAPOR definition of the response rate—that is, the weighted number of completed interviews with eligible participants divided by the estimated number of eligible individuals.8 From the MIS (see Table 2 of Part A), we have demographic information on the age, gender, race/ethnicity, marital status, number of children, and household size at baseline for individual study participants. We also have baseline data on the individuals’ education level and the characteristics of the last job and years worked prior to random assignment. For individuals who obtained services from the ITA programs, we have information on the receipt of re-employment, education and training, and support services.
Overall response rates will be computed for the full sample and by site. Response rates will then be computed for subgroups to examine if these differ systematically from overall response rates. We will compute four measures of differences in subgroup response rates relative to overall response rates:
Simple difference: Rate for a specific category – overall rate
Absolute difference: the absolute value of the simple difference ( | Rate for a specific category – overall rate| )
Relative simple difference: the simple difference divided by the overall rate ([Rate for a specific category – overall rate] / overall rate)
Relative absolute difference: the absolute difference divided by the overall rate ([ |Rate for a specific category – overall rate| ] / overall rate)
We will review these measures and describe the patterns in nonresponse. This analysis will only assess the response patterns as simple “main effects.” The third step will assess potential interactions in response patterns among subgroups.
Compare the characteristics of respondents and nonrespondents
Next, we will examine the distributions of respondents and nonrespondents along characteristics based on the administrative and wage records data. Estimates will be generated using the initial (sampling) weights for nonrespondents and respondents. Differences will be evaluated using simple t-statistics. This type of analysis can be useful in identifying patterns of potential nonresponse bias, but can be affected by small sample sizes and generally has low power to detect substantive differences. The large number of statistical tests conducted can also result in high rates of Type I error.
We will examine the differences in characteristics between the ITA2 respondents and nonrespondents, as well as between the ITA2 respondents, ITA1 respondents who did not respond to ITA2 survey, and nonrespondents to both surveys. The latter comparisons will help us describe changes in respondent characteristics across the follow-up surveys.
Identify the best explanatory factors of nonresponse and generate nonresponse weight adjustments
Logistic regression modeling is commonly used to develop adjustment factors for nonresponse, also known as response propensity modeling. Response propensity modeling using logistic regression can be viewed as an extension of the classical weighting-class nonresponse adjustment procedure that makes it possible to include more factors (that is, binary, categorical, and continuous factors) in nonresponse adjustments. To simplify the process, Chi-square automatic interaction detection (CHAID) is commonly used to assist in identifying potentially significant interactions among the subgroups or factors available for all individuals. We plan to use CHAID, with the initial sampling weights, to help identify the interactions in a multiple pass process.
The CHAID algorithm partitions the sample in a hierarchical fashion, with each successive splitting of the sample identified by CHAID. CHAID uses the Chi-square statistic with the proportion responding defined as the dependent variable to determine the partitioning of the sample with the largest value for the statistic among all possible partitions by the factors available. After the initial partitioning, the Chi-square statistic is again used to identify additional partitions subject to pre-determined restrictions (for example, a minimum partition size).
Because such “hierarchical” splitting can miss potentially important interactions, after the first CHAID analysis, we remove the initial “branching” variable and rerun the CHAID algorithm with this variable excluded. If the CHAID analysis reveals the same basic branching pattern for response rates, we proceed to the logistic modeling step (described below). If not, we remove the initial branching variable for the second CHAID analysis and rerun the CHAID algorithm a third time. Our experience is that three CHAID steps are sufficient to identify the most important interaction terms.
Next, we develop variables that reflect the interaction terms identified through the CHAID analyses, and use these variables in forward and backward step-wise logistic regressions to eliminate redundant interaction variables and to identify the most significant interactions. The step-wise logistic regressions are conducted using SAS software with normalized weights. However, the SAS software for step-wise logistic regression does not account for the sampling design. Hence, we use SUDAAN to develop the final model, so variance estimates for the coefficients reflect the sampling design. Goodness-of-fit for the final model is assessed using the percentage of concordance and discordance, the R-square for the model, and the Hosmer-Lemeshow Goodness-of-fit Test test statistic.
The final response propensity model described above will be used to identify factors associated with nonresponse and to compute the appropriate nonresponse adjustment factors for the sampling weights. The inverse of the predicted propensity to respond will be used as an adjustment factor to the initial sampling weights. These response-adjusted weights will then be post-stratified to baseline marginal totals for the full study population and will be the final analysis weights.
Compare the fully-adjusted weighted distributions of respondents along baseline characteristics to the distributions for the full sample
In this last step, we will generate estimates of the distribution of respondents along baseline characteristics using the fully-adjusted analysis weights and compare these distributions to the known totals for the full study population and for key subgroups. Analogous to the assessment of response rates, we will compute four measures of differences relative to the full sample:
Simple difference: Weighted estimate for respondents – frame total for a specific category
Absolute difference: the absolute value of the simple difference ( | Weighted estimate for respondents – frame total for a specific category | )
Relative simple difference: the simple difference divided by the frame total ([Weighted estimate for respondents – frame total for a specific category] / Frame total)
Relative absolute difference: the absolute difference divided by the overall rate ([ |Weighted estimate for respondents – frame total for a specific category | ] / Frame total)
This analysis can highlight measures where the potential for nonresponse bias is greatest and where greater caution should be exercised in the interpretation of the observed findings.
In summary, the availability of the administrative and wage records data will allow a very in-depth assessment of any potential for nonresponse bias and the estimates that may be affected. We will use the results of this nonresponse bias analysis in the preparation of the reports to highlight substantive topics that are unlikely to be affected by nonresponse bias and to provide appropriate cautionary statements for findings that may be vulnerable to nonresponse bias.
4. Tests of Procedures or Methods
A pretest of the ITA2 survey was conducted by telephone from June 24 to June 26, 2008. A total of eight interviews were completed. Pretest sample members were drawn from all eight ITA study grantees, and included both those who did and did not complete the original ITA follow-up survey. Each sample member was sent an advance letter notifying them of the interview several days before they were contacted and were offered $25 for completing an interview. All interviews were monitored by project staff for potential modifications to the instrument.
Pretest interviews ranged from 9 to 23 minutes in length. The shortest interview involved a respondent who had not participated in training and had not had any employment since the previous interview. On average, pretest interviews took 18.4 minutes to complete.
Overall, the instrument worked well in terms of the appropriateness of questions, organization, and respondent burden. Respondents were able to understand the questions and provide answers. Changes to the questionnaire based on pretest results included only additional probes and introductory statements used to aid respondent recall and clarify questions. Questions asking respondents to recall specific timelines in providing training and employment history were identified as the most likely potential sources of response error. As a result, the CATI questionnaire program will include a summary screen of reported dates on such questions and interviewers will be trained to aid respondents in verifying that information as carefully as possible.
The pretest did not include any refusal conversion attempts. The cooperation received from sample members during such a brief field period—including surveys completed by two sample members who had not completed the first ITA follow-up survey—appears to relate directly to the $25 incentive offered at the outset of the interview. Based on our pretest experiences, we anticipate that offering a $25 incentive will help elicit the levels of response and cooperation that the ITA2 study requires from sample members.
5. Individuals Consulted on Statistical Methods
The ITA2 study is being conducted by MPR under contract to DOL. Dr. Irma Perez-Johnson is the project director. Dr. Perez-Johnson is responsible for overseeing the specification and implementation of statistical methods that will be used to analyze survey and other data for the experiment. In this endeavor, Dr. Perez-Johnson will be assisted by two MPR economists: Dr. Kenneth Fortson (telephone 312-867-0496) and Dr. Quinn Moore (919-240-4879). The following individuals were consulted in developing the design, the data collection plan, the follow-up questionnaire, and the analyses for the initial evaluation of the ITA Experiment, and/or modifications for the extension study.
Name |
Affiliation |
Telephone Number |
Dr. Irma Perez-Johnson |
Mathematica Policy Research |
(609) 275-2339 |
Dr. Kenneth Fortson Dr. Quinn Moore |
Mathematica Policy Research Mathematica Policy Research |
(312) 867-0496 (919) 240-4879 |
Dr. Paul Decker |
Mathematica Policy Research |
(609) 275-2290 |
Dr. Sheena McConnell |
Mathematica Policy Research |
(202) 484-4518 |
Ms. Pat Nemeth |
Mathematica Policy Research |
(609) 275-2294 |
Dr. Dan Kasprzyck |
Mathematica Policy Research |
(202) 264-3482 |
Dr. Frank Potter Mr. John Hall Dr. John Eltinge |
Mathematica Policy Research Mathematica Policy Research Bureau of Labor Studies |
(609) 936-2799 (609) 275-2357 (202) 691-7404 |
Dr. Ralph Smith |
Congressional Budget Office |
(202) 225-3149 |
References
Groves, R.M., F.J. Fowler, M.P. Couper, J.M. Lepkowski, E. Singer, and R. Tourangeau. Survey Methodology. New York: Wiley, 2004.
Groves, R.M., M.P. Couper, S. Presser, E. Singer, R. Tourangeau, G.P. Acosta, and L. Nelson.. “Experiments in Producing Nonresponse Bias.” Public Opinion Quarterly, vol. 70, no. 5, 2006, pp. 720-736.
Groves, Robert M. “Nonresponse Rates and Nonresponse Bias in Household Surveys.” Public Opinion Quarterly, vol. 70, no. 5, 2006, pp. 646-675.
McConnell, Sheena, Elizabeth Stuart, Kenneth Fortson, Paul Decker, Irma Perez-Johnson, Barbara Harris, and Jeffrey Salzman. “Managing Customers’ Training Choices: Findings from the Individual Training Account Experiment.” Washington, DC: Mathematica Policy Research, Inc., December 2006. (Report available at http://www.mathematica-mpr.com/publications/PDFs/managecust.pdf; technical appendices available at: http://www.mathematica-mpr.com/publications/PDFs/managecustappendices.pdf.)
Olson, Kristin. “Survey Participation, Nonresponse Bias, Measurement Error Bias, and Total Bias.” Public Opinion Quarterly, vol. 70, no. 5, 2006, pp. 737-758.
Stapulonis, Rita A., Martha D. Kovac, and Thomas M. Fraker. “Surveying Current and Former TANF Recipients in Iowa.” Paper presented at the 21st Annual Research Conference of the Association for Public Policy Analysis and Management, Washington, DC, November 5, 1999.
1 Section B.2 discusses the estimation of parameters of primary importance for the study.
2 The first ITA follow-up survey was conducted between November 2003 and July 2005.
3 The MDE for quarterly earnings for the original ITA follow-up survey assumes an 80 percent response rate, instead of the 70 percent response rate that we have set as the target for the ITA2 follow-up survey.
4 Appendix D in McConnell et al. (2006) presents results from a sensitivity analysis that estimates effects using differences-in-means rather than regression adjustment. The results obtained were very similar to the main results presented in the report.
5 In the original study, we found that the following characteristics were associated with the likelihood of response: earnings in the year before being randomly assigned, age, marital status, and whether the sample member had an email address.
6 For most variables, data were missing for less than 1 percent of the sample (McConnell et al., 2006). Table B.2 in the final report for the original study (McConnell et al., 2006) describes item-level nonresponse for key data items.
7 The hot-deck imputation procedures used in the original study, including diagnostic checks are discussed in detail in pages B-7 to B-9 of the final evaluation report (McConnell et al., 2006).
8 The American Association for Public Opinion Research. 2008. Standard Definitions: Final Dispositions of Case Codes and Outcome Rates for Surveys. Fifth edition. Lenexa, Kansas: AAPOR
| File Type | application/msword |
| File Title | MEMORANDUM |
| Author | Dawn L. Patterson |
| Last Modified By | naradzay.bonnie |
| File Modified | 2009-01-28 |
| File Created | 2009-01-28 |
© 2025 OMB.report | Privacy Policy