NASA SOI OMB Package _2 Part B 5-25-11
NASA SOI OMB Package _2 Part B 5-25-11.docx
Summer of Innovation #2 (Surveys)
OMB: 2700-0151
SUPPORTING STATEMENT
FOR OMB CLEARANCE
PART B
NASA Summer of Innovation FY2011
STUDENT SURVEY AND TEACHER SURVEY DATA COLLECTION
National Aeronautics and Science Administration
May 24, 2011
Contents
Part B: Collection of Information Employing Statistical Methods 3
B.2. Procedures for the Collection of Information 4
B.2.1 Statistical Methodology for Sample Selection 7
Student Descriptive Analyses: Single Time Point 9
Teacher Descriptive Analyses: Single Time Point 10
Student Descriptive Analyses: Change Over Time Analyses 10
Teacher Descriptive Analyses: Change Over Time Analyses 13
B.3 Methods to Maximize Response Rates 13
B.5 Individuals Consulted on Statistical Aspects of Design 14
Part B: Collection of Information Employing Statistical Methods
The purpose of the national evaluation is to gather data that will inform NASA’s continued development of the Summer of Innovation (SoI) project as well as to assess whether a summative, impact evaluation would be warranted at a future date. To this end, an important component of the current evaluation will focus on identifying significant changes between baseline and follow-up student and teacher surveys. While measuring outcomes at multiple points in time can provide evidence of whether the outcomes of interest change, it will not allow us to rule out the possibility that something other than the program is affecting this change. As such, we emphasize that the national evaluation is a formative study, focused on gathering information to inform promising practices.
As NASA centers are not required to serve classroom teachers, only teachers at national awardee sites will be administered surveys. These surveys will examine whether SoI teachers’ comfort in teaching NASA topics and their access and use of NASA resources changes over time. The student surveys will be administered to students at national awardees and NASA Centers to capture whether student interest in STEM changes across the evaluation periods. Surveys will be administered to classroom teachers (at national awardees only) and students at national awardees and NASA centers prior to and at the end of the summer activities. Given that linking student and teacher surveys is beyond the scope of this formative evaluation, particularly because students and teachers will not necessarily be from the same school, student and teacher surveys will be analyzed as two distinct samples. An additional teacher and student survey will be administered after the school-year activities at the national awardees; the teacher survey will be online while the third student survey will be mailed to their home address.1Because requirements for the school-year activities are minimal for the NASA Centers, their participating students will not participate in the third wave of survey data collection.
The Summer of Innovation (SoI) Project FY2011 includes three types of awards: national awardees, NASA Centers, and mini-grants, the first two of which will be included in the national evaluation. NASA will fund 10 national awardees each expected to reach 2,500 students and 10 NASA centers each expected to reach 1,500 students. NASA has set programming requirements as follows: national awardees are required to provide 40 hours of student STEM activities utilizing NASA content over the summer and an additional 25 hours by March 2012; NASA Center partnerships must provide 20 hours of student STEM activities utilizing NASA content during the summer and an additional two STEM activities integrating NASA content by March 2012. For the national awards, organizations receiving SoI funding are required to provide classroom middle school teachers 40 hours of professional development by March 2012 and use them as part of their summer staff delivering NASA content; NASA Center partnerships are not expected to provide professional development for classroom teachers.
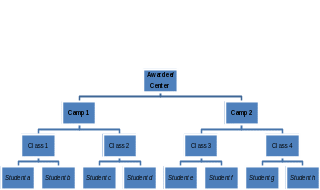
Based on a review of the national awardees’ and NASA Centers’ proposals, we expect that each awardee/Center will have between 1 and 19 camps, defined as a set of activities that take place in a specific location (e.g., school, community center, etc.). Each camp will have between 1 and 150 classes, defined as a group of students who receive the same set of SoI learning experiences. In addition, national awardees are expected to integrate at least 150 classroom teachers as part of their summer staff at each of the 10 awardees.2 As expectations and supports for awardees are different from those for NASA Centers, the national evaluation will analyze their data separately. Exhibit 1 presents an example of the expected structure of awardees/Centers.
Exhibit 1. Structure of Awardees/Centers
The target population for the teacher surveys is all classroom teachers who participate in the SoI Project in FY 2011. Teacher surveys will be administered to the census of classroom teachers participating in SoI. As a result, there will be no sampling considerations. The target population for the student surveys is all students who participate in the SoI project FY 2011. We will administer the student survey to 6,900 students, selected in accordance with the sampling plan outlined in the following section.
B.2. Procedures for the Collection of Information
Exhibit 2 presents an overview of the survey data collection at national awardee and NASA Centers. Because of differing programmatic requirements at national awardees and NASA Centers, survey administration will differ between the two programs. National awardees will administer teacher and student baseline and first follow-up surveys. As will be described in more detail in the next section, an additional student and teacher survey will be administered at these sites after the completion of the school year activities in March 2012. NASA Centers, however, will only administer student survey at two points in time, prior to and at the end of the summer activities.
Exhibit 2. Data Collection Overview |
|||
|
Baseline Survey |
Summer Follow-up Survey |
School Year Follow-up Survey |
Students at National Awardees |
X |
X |
X |
Teachers at National Awardees |
X |
X |
X
|
Students at NASA Centers |
X |
X |
N/A |
Teachers at NASA Centers |
N/A |
N/A |
N/A |
Student Surveys: Procedures for Data Collection
Baseline Student Surveys
Prior to the start of the summer program, the national evaluator will obtain Institutional Review Board (IRB) approval and provide training to awardees/Centers’ national evaluation coordinators to ensure rigorous and systematic data collection procedures. Throughout the program, the national evaluators will support the awardees/Centers in their data collection efforts.
As part of the registration process, awardees and NASA centers will obtain parent consent forms and the associated parent survey (Appendix B) from all students. The consent forms will have information about the evaluation, the purpose of data collection, potential risk, and privacy assurances. The associated survey asks for information about the student’s demographics. Parents will return the signed consent form and parent survey to the awardee/center as part of the materials required to enroll their student in the SoI activities. Students whose parents do not grant consent to participate in the national evaluation can still take part in the SoI activities.
The awardees’ national evaluation coordinators will provide the national evaluator with information about the number of students in classes and the number of classes and camps in an awardee/Center by June 1, 2011. This information will be used by the national evaluator to sample at the camp and classroom level (more detail regarding the sampling plan is provided in the next section). After sampling is complete, the national evaluator will provide the national evaluation coordinators with list of the classes and camps selected for survey administration. The national evaluation coordinator will then be responsible for ensuring the proper administration of the paper-and-pencil baseline surveys on site at the start of the program to those students with parental consent; they provide students without parental consent an alternative activity to participate in during survey administration. As is true throughout the duration of the study, consent to participate may be withdrawn at any time without penalty or change in participation status.
We expect that most students in a class will have parental consent. Parental consent rates for a program with a similar parental consent form process yielded relatively high consent rates (almost 70%; Martinez & Consentino de Cohen, 2010). Further, given that the survey is benign in nature and that there are no consequences for not granting consent, we do not expect that consenting parents will be markedly different from non-consenting parents. However, to test this assumption, we will compare demographic information for non-consenting students to those with consent. Demographic information about non-consenting students may be available from parents who fill out the parent survey (but do not give consent) or from sites collecting this information for their own data needs. Finally, survey data results will clearly state that inferences can only be made about students with consent.
First Follow-up Student Surveys
The summer (first) follow-up student survey will be administered to students with consent in sampled classrooms on the last day of students’ summer activities. Again, national evaluation coordinators will be responsible for administering surveys to consenting students and providing alternative activities to students without consent. The purpose of the summer follow-up survey is to measure changes in science interest outcomes using the same questions included in the baseline survey. As such, summer follow-up survey outcomes will be compared to those from the baseline survey.
Second Follow-up Student Surveys3
School-year (second) follow-up surveys will be mailed to the home addresses of students with parental consent who participated in summer activities at awardees after the completion of the school-year activities in March 2012 (students who participated in summer activities at NASA Centers will not be administered a third survey, as requirements for school year follow-up activities are minimal). The purpose of the school year follow-up survey is to measure if science interest is sustained over the course of the school year using the same questions as the summer follow-up survey. We expect that some of the students will move between the time their parents completed the parent survey and when we would mail the survey. Accordingly, we will email parents an online form in late 2011/early 2012 allowing them to update their address information. In addition, we will perform one updating of parent addresses using the Lexis Nexus database. If response rates to the mailed survey are low, the national evaluation team will follow up with students using the email addresses and phone numbers provided by parents on the consent form.
Classroom Teacher Surveys: Procedures for Data Collection
Baseline Classroom Teacher Surveys
Classroom teachers at awardees who register to participate in the SoI program will receive a registration packet that includes registration materials and the baseline survey (because there are no classroom teacher requirements at NASA Centers, any teachers participating there will not be administered surveys). The national evaluation coordinators will be responsible for instructing teachers to complete the baseline survey included in the registration packet, collecting the registration packet, and returning the baseline surveys to the national evaluator.
First Follow-up Classroom Teacher Surveys
The registration materials collected at the beginning of SoI programming will contain the classroom teacher’s contact information, including their email address. The email address included in the registration form will be used to send classroom teachers a message asking them to complete an online survey immediately at the end of SoI summer activities. Similar to the student surveys, the teacher surveys are designed to detect changes in outcomes between the follow-up summer survey and baseline survey using the same questions across survey waves. In the event that classroom teachers do not respond to the email (or it bounces back), we will use additional information from the registration forms (e.g., phone number) to follow up with teachers by sending up to three email reminders and making up to three follow-up calls to encourage them to fill out the online survey at home or wherever they have internet access. We will also offer them the option of taking a paper and pencil survey that we will mail to them along with a pre-paid, pre-addressed, Business Reply Envelope. Two national awardees have indicated that their teachers may not have internet access. We will print paper surveys and mail them to the national coordinator for administration.
Second Follow-up Teacher Surveys4
An email message asking teachers to complete a school year follow-up survey will be sent to teachers in March 2012 to detect any differences between school year follow-up and summer follow-up surveys. In the event that classroom teachers do not respond to the email (or it is bounced back), we will use additional information from the registration forms (e.g., phone number) to follow up with teachers by sending up to three email reminders and making up to three follow-up calls to encourage them to fill out the online survey at home or wherever they have internet access. We will also offer them the option of taking a paper and pencil survey that we will mail to them along with a pre-paid, pre-addressed, Business Reply Envelope. Two national awardees have indicated that their teachers may not have internet access. We will print paper surveys and mail them to the national coordinator for administration.
B.2.1 Statistical Methodology for Sample Selection
Sampling Plan
Sampling Frame for Teacher Surveys
The teacher respondent universe of 1,500 is based on NASA requirements included in the solicitations for the national awards. Each of the 10 national awardees will be included in the teacher survey sample and each awardee is expected to integrate at least 150 classroom teachers into the summer activities. The universe of classroom teachers participating in SoI at awardees will be asked to complete the teacher surveys; thus, there are no sampling considerations.
Sampling Frame for Student Surveys
The student respondent universe of 40,000 is based on NASA requirements included in the solicitation for national awardees and NASA Centers. National awardees are expected to reach 25,000 students and NASA Centers are expected to reach 15,000 students. Given the limitations of surveying such a large number of students, a sample will be drawn to obtain a representative sample of students, as described in more detail in the following section.
Power Calculations for Student Surveys
We used power calculations to estimate the number of students that would have to be sampled at each awardee/Center to detect a minimum detectable effect size of .1 on science interest measures between survey waves with 80% power, assuming a two-sided test at 5% level of significance with a correlation between students across waves of .5 and a population standard deviation of 1.14. We consider a change of 0.1 to be substantive for purposes of deciding on changes for the project, as differences between the summer follow-up survey and the baseline survey ranged between -.1 and .1 in last year’s pilot surveys. Based on results from last year’s pilot, we assumed a response rate of 85% and an attrition rate of 30% for each follow-up wave. Because students are clustered within classes and classes are clustered within camps, the sample size was inflated using a design effect of 1.4 to account for intraclass correlation5. The results of the power calculations, including adjustments for response rates, attrition, and the design effect, indicate that we will have to sample a total of 3,450 students at awardees and a total of 3,450 students at NASA centers. Thus, we will sample a total of 6,900 students.
Sampling Method
Within each awardee/Center, students will be sampled using a three-stage cluster sampling design to obtain a representative sample of SoI students. First, we will select a systematic sample of camps at each awardee/center. Systematic sampling after sorting by size increases the likelihood of having a wide distribution of camp sizes in the selected sample. Next, we will take a systematic sample of classes within each camp. Again, the systematic sample will be taken after sorting classes by size, as we expect class sizes to differ within camps. Finally, within classes, all students with parental consent will be administered a survey. The resultant sample of students will be clustered (or nested) within sampled classes and camps. This strategy will be utilized for each awardee/Center to enable separate analyses for these subpopulations. The three-stage sampling plan for a given awardee/Center is depicted in Exhibit 3.
Exhibit 3. Three-stage Cluster Sampling Plan for each Awardee/Center |
||
Stage |
Sampling Unit |
Systematic Factors |
1 |
Camps |
Camp size |
2 |
Classes |
Class size |
3 |
Students |
N/A |
Each of the 10 NASA Centers and 10 national awardees will be included in the student survey sample. The number of students to be sampled within each awardee/Center will be determined using allocation proportional to the number of students within each awardee/Center (note that although each awardee/center is expected to reach a minimum number of students, we expect that each awardee/center will vary in the number of students they reach). As such, the number of students needed from each awardee/center (SSi) can be calculated as (acknowledging that these targets may have to be adjusted once we obtain the number of students enrolled at each awardee/center):
![]() ;
where
;
where
SS is the required sample size across all awardees (SS=3,450) and all Centers (SS=3,450);
![]() is
the total number of students engaged in SoI activities at the ith
awardee/Center; and
is
the total number of students engaged in SoI activities at the ith
awardee/Center; and
N is the total number of students engaged in SoI activities across all awardees/Centers.
For example, the required sample size across all national awardees is 3,450. If national awardees have enrolled a total of 28,000 students and National Awardee A has enrolled 3,300 students, using the formula above, National Awardee A would have to sample about 400 students. If National Awardee A has 3 camps, 6 classes, and 50 students within each class, we would systematically select 2 camps and 4 classrooms from each camp for a total of 400 students.
Sampling Weights
To produce population-based estimates, each responding student will be assigned a sampling weight. The sampling weight is a combination of a base weight and an adjustment for student non-response to the survey. The base weight is the inverse of the probability of selection of the responding student. The probability of selecting a student is the product of the probability of selecting the camp in which the student is located in an awardee/Center and the probability of selecting the class to which the student belongs within the selected camp. The overall base weight is the product of the camp weight and the class weight. The weights of responding students in a class are adjusted to account for students who belong to that class but do not respond. The non-response-adjusted weights are used for producing estimates and for all statistical analyses.
As we are surveying the universe of teachers and expect a high response rate (as noted in Section B.3), no weights are needed to produce population-based teacher estimates.
Student Descriptive Analyses: Single Time Point
When the appropriate weights are used, our sampling design allows for the calculation of representative, cross-sectional averages of survey data at the student level across all awardees/Centers and at the awardee/Center level.
Student Outcomes Across All Awardees/Centers
To make statements about, “the percent of students that..,” we will design our analysis such that the interpretation of “percent of students” corresponds to the percent of students out of all SoI students, not just the students that happen to be in the sample. In order to calculate statistics that are representative of all SoI students, the sampling design must be taken into account. We provide the calculation algorithm below. Note that if the survey item is dichotomous (0/1), then the process described below to estimate a mean actually results in the estimation of a proportion. Multiplying the proportion by 100 will give a percentage.
Let:
yhij be the response on a survey item for student j in class i and camp h,
whij = the sampling weights for student j in class i across all awardees/centers and camp h across all awardees/centers, adjusted for non-response
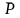 = the estimator of the population percentage,
= the estimator of the population percentage,
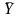 = the estimator of the population mean,
= the estimator of the population mean,
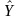 = the estimator of the population total,
= the estimator of the population total,
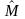 = the estimator of the number of elements (students) in the
population,
= the estimator of the number of elements (students) in the
population,
h = 1, ..., L enumerate the camps,
i = 1, ..., I enumerate the classes,
j = 1, ..., nj , enumerate the sampled students in camp h and class i
Then:
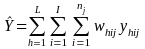 ,
,
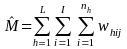 ,
,
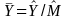 ,
,
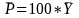
Student Data at the Awardee/Center Level
In the event that we would like to make a statement about, “the percent of students at Awardee A that...,” we will design our analysis such that the interpretation of “percent of students at Awardee A” corresponds to the percent of students out of all SoI students at the awardee/center, not just the students that happen to be in the sample. In order to calculate statistics that are representative of all students at a particular awardee/center, we will apply the same calculation algorithm described above, but adjust the weight to reflect all students at a particular awardee/center rather than all students across awardees/centers.
Teacher Descriptive Analyses: Single Time Point
Teacher Data Across and Within Awardees
Because the universe of teachers will be sampled, to make a statement about, “the percent of teachers that ....,” or “the percent of teachers within an awardee that…,” our descriptive statistics for a single point in time do not need to be adjusted for a sampling design. Means and standard deviations will be used to describe central tendency and variation for survey items using continuous scales. Frequency distributions and percentages will be used to summarize answers given on ordinal scales. Descriptive analyses about all awardees will be conducted on the full teacher sample, while descriptive analyses about teachers within particular awardees will be restricted only to respondents from that awardee.
Statistical Software for Calculating Parameter Estimates and Standard Errors
For the student analyses, the estimator of the population mean can be easily calculated in statistical software packages that are designed for analysis of complex survey data including the estimation of mean and variance (e.g. SAS, SUDDAN). We can use the variance estimates to produce standard errors and 95% confidence intervals around the estimates of the population means for the student level data. The teacher descriptive statistics can also be easily calculated in statistical software packages (e.g., SAS, SUDDAN).
Student Descriptive Analyses: Change Over Time Analyses
By “change over time analyses,” we mean simple descriptions of change in a variable over time. This is distinct from a model where we try to assess the relationship between some predictor variable(s) and the change in the outcome variable over time.
Difference in Proportions over Time for Student Sample
We plan on testing whether the difference in proportions between two time points is zero. We specify the null and alternative hypotheses as:
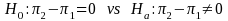
where
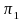 and
and
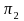 are population proportions, and
are population proportions, and
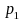 is an estimate of the proportion obtained from the first sample
is an estimate of the proportion obtained from the first sample
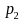 is
the proportion in the second.
is
the proportion in the second.
In addition to reporting the estimated difference between two population proportions from two points in time, the precision of the estimate needs to be reported. This is done by computing the standard error of the estimated difference. The simple case has two independent samples at the two time points, thus, the variance of the difference between the two sample proportions is simply the sum of the variance of the first proportion and the variance of the second proportion.
The SoI study, however, is not an example of the
simple case. Rather, the same population is surveyed at both time
points. Therefore, the variance of the difference is no longer
a sum of the variances; rather, it also includes a covariance. The
variance of the difference is smaller than if there were two
independent samples. The degree to which the variance in the
estimate for the overlapping samples is reduced depends on the amount
of overlap and the correlation coefficient between the estimates at
two time periods. Kish (1965) provides a formula that computes the
variance of the difference taking into account the amount of overlap
and the correlation between two time periods as described below.
Let
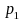 denote the estimated proportion from the baseline sample, with sample
of size
denote the estimated proportion from the baseline sample, with sample
of size
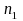 .
Let
.
Let
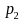 denote the proportion from the follow-up sample, with sample of size
denote the proportion from the follow-up sample, with sample of size
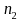 .
Let
.
Let
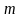 denote the amount of overlap between the two samples. We are
interested in obtaining the standard error of the difference between
the two sample proportions. We can write the estimated variance of
the difference between the two sample proportions as:
denote the amount of overlap between the two samples. We are
interested in obtaining the standard error of the difference between
the two sample proportions. We can write the estimated variance of
the difference between the two sample proportions as:
where, is
the estimated variance of the baseline proportion based on a sample
of
is
the estimated variance of the baseline proportion based on a sample
of
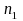 units and
units and
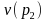 is
the estimated variance of the post proportion based on
is
the estimated variance of the post proportion based on
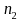 units.
units.
Under simple random sampling, the estimated variance of the difference in two sample proportions becomes
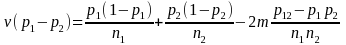
where
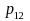 is the proportion having the attribute in both the samples based on a
sample of
is the proportion having the attribute in both the samples based on a
sample of
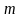 units. The student-level data from the two samples must be merged to
calculate the quantity
units. The student-level data from the two samples must be merged to
calculate the quantity
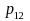 .
.
For estimating the variance under the complex design used in SoI and proposed for the current study, we can first estimate the variance under simple random sampling using the formula given above but with weighted proportions. Then, we multiply the variance by the design effect.
To implement this method we will obtain the
variances under the complex design for the two samples using SAS as
the values for
 and
and
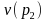 ,
and estimate the covariance as
,
and estimate the covariance as
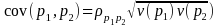 ,
,
where the correlation term
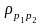 is calculated as the correlation between baseline and follow-up
survey measurements for the students that were measured at both time
points.
is calculated as the correlation between baseline and follow-up
survey measurements for the students that were measured at both time
points.
The square root of the variance gives the standard error of the difference in the two proportions recognizing that we have overlapping samples and thus that the samples are not independent. The standard error will be used in a statistical test of the null hypothesis of equivalent proportions in the two groups. The specification of the hypothesis test is,
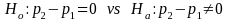
and procedure for determining the test statistic is:
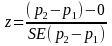
If the observed value of z as calculated above is greater than the critical value for α=0.05 from the z-distribution (1.96), the null hypothesis will be rejected at the p<0.05 level.
Difference in Means over Time for Student Sample
If the goal of the calculations is to perform a test of whether the difference between two means from two points of data collection is equal to zero then the challenging part of conducting the test is again calculating the variance of the difference of the means.
In order to calculate the variance (and standard
error) of the difference (Kish, 1965), let
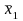 denote the estimated mean from the first sample of size
denote the estimated mean from the first sample of size
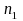 .
Let
.
Let
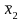 denote the estimated mean from the second sample of size
denote the estimated mean from the second sample of size
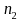 .
We are interested in testing the difference between the two sample
means. We can write the estimated variance of the difference
between the two sample means as:
.
We are interested in testing the difference between the two sample
means. We can write the estimated variance of the difference
between the two sample means as:
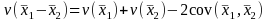
Under our sampling design, the variance of the difference can be written as
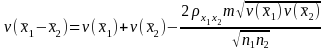 ,
,
where
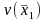 is
the estimated variance of the first mean based on a sample of
is
the estimated variance of the first mean based on a sample of
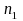 units,
units,
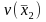 is
the estimated variance of the second proportion based on
is
the estimated variance of the second proportion based on
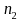 units and
units and
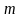 is the amount of overlap between the two samples. The correlation (
is the amount of overlap between the two samples. The correlation (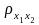 )
is estimated based on the overlap. SAS can calculate the variance
under our sampling design for the first mean and for the second mean.
)
is estimated based on the overlap. SAS can calculate the variance
under our sampling design for the first mean and for the second mean.
The square root of the variance gives the standard error of the difference in the two means, which can be used in a statistical test recognizing that we have overlapping samples and they are not independent. The specification of the hypothesis test is,
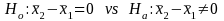
and procedure for determining the test statistic is:
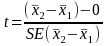
If the observed value of t as calculated above is greater than the critical value from the t-distribution with n –2 degrees of freedom and α=0.05, the null hypothesis will be rejected at the p<0.05 level.
Teacher Descriptive Analyses: Change Over Time Analyses
Similar to the student analyses, we will conduct simple descriptions of change in a variable over time for classroom teacher outcomes. Again, this is distinct from a model where we try to assess the relationship between some predictor variable(s) and the change in the outcome variable over time.
Difference in Teacher Outcomes over Time
We plan on testing whether the difference in proportions and/or means for teachers between two time points is zero. To do so, we will use a McNemar test or paired t-test, depending on the distribution of the outcome variables.
B.3 Methods to Maximize Response Rates
The key for maximizing response rates is to provide multiple opportunities for students and teachers to complete the survey while they participate in the SoI activities. Several methods will be used to maximize response rates and address non-response, such as:
Providing opportunities during the summer camp sessions to complete the student survey at the beginning and end of the summer activities;
Asking teachers to fill out the baseline survey as a part of their registration packet. A webinar for national evaluation coordinators will be conducted prior to survey distribution that will emphasize the importance of collecting the baseline survey before the start of SoI programming. The national evaluation coordinators will be responsible for collecting these surveys for each camp.
Giving teachers the opportunity to fill out follow-up surveys via an online link. Our procedures for the follow-up surveys include sending up to three email reminders and making up to three follow-up calls to encourage teachers to fill out the surveys at home or wherever they have internet access. Two national awardees have indicated that their teachers may not have internet access. For these awardees, we will print paper surveys and mail them to the national coordinator for administration.
Designing two different versions of the student surveys that each take minimal effort (burden) and are at the appropriate reading level for younger and older middle school students.
Given that students will have opportunities to fill out the baseline surveys during summer programming, we expect to achieve a response rate of 85% or higher for the baseline survey. We assume that some attrition will occur, particularly if a third survey is mailed to students after the school year activities. Given that attrition rates for the pilot student surveys were about 30% between baseline and summer follow-up, we expect a response rate of about 70% for the summer follow-up survey and about 49% for the school year follow-up survey.
For teachers, we expect to achieve response rates of 85% or higher for the baseline survey. We assume that some attrition will occur between the baseline and summer follow-up survey and between the summer follow-up survey and the school-year follow-up survey. Based on the pilot teacher survey attrition rates of 10% between survey waves, we would expect a response rate of about 77% at summer follow-up and about 69% at school year follow-up.
Nonresponse Bias
Nonresponse may be a problem in our analyses if it introduces bias into our population estimates. Bias occurs if the students that refuse to participate or leave the study would give systematically different responses to the survey (had they responded to it) than the students who complete the surveys. Poor response rates do not guarantee a biased estimate, as the decision to not participate or leave the study could be completely unrelated to survey answers.
In general, the effects of potential non-response bias cause little concern if the non-response rate is less than 20 percent; accordingly, we will conduct a nonresponse bias analysis that is described below, if our response rate is less than 80 percent. We will construct a propensity model to estimate the probability of a student responding to the survey (propensity score) both for responding and nonresponding students. These propensity scores are estimated by a logistic regression model that will use demographic variables (e.g., gender, grade level, race, ethnicity) collected on the original parent consent form/survey that will be available both for nonresponding and responding students. We will then group students using the estimated propensity scores and examine the demographic characteristics of responding and nonresponding students within each group. This grouping will provide a method of forming weighting classes to adjust the weights of responding students and reduce nonresponse bias.
Survey development and procedures were tested and refined as follows. Last year’s pilot surveys were fielded in summer 2010, revised in fall 2010, and updated in winter 2010 to measure outcomes of interest in FY2011. For the student surveys, existing instruments with established psychometric characteristics were selected after an extensive literature review (e.g., Modified Attitudes Towards Science Inventory (mATSI), Weinburgh and Steele, 2000; Test of Science Related Attitudes (TOSRA), Fraser, 1981; and the Math and Science Interest Survey, Hulett, Williams, Twitty, Turner, Salamo, and Hobson, 2004). The student surveys were piloted with seven middle school students to further refine the language and estimate time for completion.
Key questions on the teacher survey were designed specifically for the SoI evaluation and constructed to capture outcomes from the program’s logic model. Teacher background questions were taken from existing, nationally fielded instruments (see Appendix 7). The surveys, including the newly constructed questions, were piloted with six teachers to test and refine the language and estimate time for completion. In addition, experts in the field reviewed draft and final instruments for content validity and clarity, In addition, experts in the field reviewed draft and final instruments for content validity and clarity, including Marian Pasquale, Senior Research Scientist at the Education Development Center (EDC) and a former middle school teacher, with expertise in middle school curriculum development, technology implementation, and student learning. Finally, NASA Office of Education staff reviewed the instruments for final approval.
B.5 Individuals Consulted on Statistical Aspects of Design
The plans for statistical analyses for this study were primarily developed by Abt Associates, Inc. and the Education Development Center (EDC). The team is led by Hilary Rhodes, Project Director; Ricky Takai, Principal Investigator; Alina Martinez, Principal Associate; Amanda Parsad, Project Quality Advisor; Kristen Neishi, Deputy Project Director; Melissa Velez, Survey Analysis Task Leader, and K.P. Srinath, Survey Statistician, all of Abt Associates, Inc. The surveys were refined by Jacqueline DeLisi, Abigail Levy, and Yueming Jia at EDC. Contact information for these individuals is provided below.
Abt Associates, Inc. |
|||
Hilary Rhodes |
Project Director |
617-520-3516 |
|
Alina Martinez |
Principal Associate |
617-349-2312 |
|
Ricky Takai |
Principal Investigator |
301-634-1765 |
|
Amanda Parsad |
Project Quality Advisor |
301-634-1791 |
|
Kristen Neishi |
Deputy Project Director |
301-634-1759 |
|
Melissa Velez |
Survey Analysis Task Leader |
617- 520-2875 |
|
K.P. Srinath |
Survey Statistician |
301-634-1836 |
|
Education Development Center |
|||
Jacqueline DeLisi |
Survey Task Leader |
617-969-5979 |
|
Abigail Levy |
Survey Developer |
617-969-5979 |
|
Yueming Jia |
Survey Developer |
617-969-5979 |
|
Kish, L. (1965). Survey Sampling. New York: John Wiley & Sons, Inc.
Lohr, S. L. (1999). Sampling: Design and Analysis. Pacific Grove, CA: Brooks/Cole Publishing Company.
Martinez, A. & Consentino de Cohen, C. (March 31, 2010). The National Evaluation of NASA’s Science, Engineering, Mathematics and Aerospace Academy (SEMAA) Program. Cambridge, MA: Abt Associates, Inc.
1 Note: This package is the second of three for the SoI formative evaluation. It focuses on the data collection efforts scheduled between June 2011 and November 2011; the first package, submitted on March 25, 2011, requested clearance to collect parent consent forms and the associated short survey and awardee planning information prior to June 2011. The third package will include materials for activities occurring between December 2011 and March 2012, including the third survey administration. It was necessary to submit the first package before the current one so that NASA may collect key baseline data – including parent consent and awardee plans for implementation- prior to the start of this year’s activities and also have sufficient time to examine proposals, make awards, and use the proposal information to inform the evaluation’s sampling strategy and data collection.
2 In addition to classroom teachers, awardees/Centers will also likely use informal educators, such as youth development leaders, to implement the camps. However, they are not currently a main focus of NASA’s SoI design and therefore are not surveyed along with the classroom teachers.
3 The emergency clearance would not include survey data collected in the third wave as it falls outside of the cleared time frame. We include it in the description to articulate our vision for the national evaluation. A subsequent OMB package will be prepared to obtain clearance for the third wave of survey data.
4 The emergency clearance would not include survey data collected in the third wave as it falls outside of the cleared time frame. We include it in the description to articulate our vision for the national evaluation. A subsequent OMB package will be prepared to obtain clearance for the third wave of survey data.
5 Note that the survey analysis team selected this design effect based on previous experiences with similar sampling designs and populations.
6 Note that m may be close to 1 as samples may be fully overlapping.
National
Aeronautics and Space Administration Part B: Collection of
Information
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | Abt Double-Sided Body Template |
| Author | Abt Associates Inc |
| File Modified | 0000-00-00 |
| File Created | 2021-01-31 |
© 2025 OMB.report | Privacy Policy