SEBTC Revised OMB Part B 3 16 11 final
SEBTC Revised OMB Part B 3 16 11 final.doc
Evaluation of the Impact of the Household-Based Summer Demonstrations on Food Insecurity Among Children (SEBTC)
OMB: 0584-0559
OMB
Submission: Part B—Statistical Methods
Evaluation
of the Impact of the Summer Food for Children Household-Based
Demonstrations on Food Insecurity
March
16, 2011
Abt
Associates Inc. 55
Wheeler Street Cambridge,
MA 02138
Submitted
to: Hoke
Wilson, Ph.D. USDA/FNS/ORA 3101
Park Center Drive, Room 1043 Alexandria,
VA 22302

![]()
Contents
B.1.1 Sampling Frame and Household Identification 1
B.1.5 Two-Phase Sampling Plan 6
B.1.7 Analysis of Nonresponse Bias 10
B.2 Procedures for the Collection of Information 11
B.2.1 Statistical Methodology for Stratification and Sample Selection 11
B.2.2 Estimation Procedures 11
B.2.3 Degree of Accuracy Needed: Statistical Power and Minimum Detectable Differences 25
B.2.4 Unusual Problems Requiring Specialized Sampling Procedures 28
B.2.5 Use of Periodic Data Collection Cycles to Reduce Burden 28
B.3 Methods to Maximize Response Rates and Deal with Nonresponse 29
B.4 Tests of Procedures or Methods to be Undertaken 30
B.5 Individuals Consulted on Statistical Aspects and Individuals Collecting and/or Analyzing Data 30
Part B of the Justification for this information collection activity, the FNS Evaluation of the Impact of the Summer Food for Children Household-based Demonstrations on Food Insecurity (SEBTC Benefit Demonstration), addresses the five points outlined in Part B of the OMB guidelines.
B.1 Respondent Universe and Sampling Methods.
Describe (including a numerical estimate) the potential respondent universe and any sampling or other respondent selection method to be used. Data on the number of entities (e.g., establishments, State and local government units, households, or persons) in the universe covered by the collection and in the corresponding sample are to be provided in tabular form for the universe as a whole and for each of the strata in the proposed sample. Indicate expected response rates for the collection as a whole. If the collection had been conducted previously, include the actual response rate achieved during the last collection.
In this section, we describe the procedures that will be used to select the sample of households and children for the evaluation of the SEBTC benefit demonstrations, including:
Sampling frame and household identification;
Procedures for obtaining informed consent;
Random assignment to the treatment and control conditions;
Sample sizes;
Use of a two-phase sampling plan; and
Response rates.
B.1.1 Sampling Frame and Household Identification
Each grantee has specified a geographic area for the demonstration that includes one or more SFAs, all of whom agreed to participate in the demonstration and evaluation. The sampling frame for the evaluation includes school children in grades K-12 certified for free or reduced-price NSLP meals in the SFAs that are part of the demonstration areas. However, since SEBTC benefits are at the household-level, not individual child-level, the appropriate sampling unit is household, not child. A household is eligible to participate in the demonstration if it includes at least one certified child in grades K-12.
The sampling frame will include a list of eligible children. Ongoing discussions with SFAs are currently clarifying what additional information will be available for all children in the sampling frame. It seems likely that we will have information on gender, grade, and perhaps age/date of birth and race/ethnicity. Those are variables that are likely to appear in SFA administrative data records.
Sampling frame information will not include any information on income. This is unfortunate. It seems plausible that VLFS is more common among poorer children. Thus, if we had information on income, we could have higher prevalence and smaller samples (or more precise estimates) by oversampling lower income families. However, information on income will not be on the frame making it infeasible to oversample poor households.1
Because household contact information cannot be released to the evaluator without parental consent, grantees, working with technical assistance as needed from the evaluator, will be responsible for recruiting households and obtaining their consent for participation in the program. Once consent is obtained, Abt Associates will be responsible for selecting the sample of households to receive the SEBT for Children benefits, as well the households to participate in the evaluation.
For some grantees, constructing the household-level data file may be relatively straightforward; they can use household identifiers in existing databases. Other grantees may require guidance from the evaluation team on methods for aggregating data from the child level to the household level. For the purposes of the demonstration, a household will be defined as the unit identified in the NSLP application or, for those directly certified, the unit in the SNAP/TANF case.
The evaluation team will work closely with the grantees and SFAs to construct these household lists. We will assign a team of evaluation staff to the SFAs in each demonstration area to help them assemble household lists from students certified for NSLP. This team will also provide advice on the consent process, if requested. The same team that provided the technical assistance to the SFAs will then conduct the process study for the demonstration area. Technical staff will be assigned to oversee the list construction process across all sites, to review lists. Mike Battaglia, Abt’s most senior sampling statistician, will conduct random assignment of consenting households. in each of the demonstration sites.
The level of support to be provided to grantees will vary with what activities each grantee indicates that it can or must do itself. For the POC year, the grant applications indicate that all sites plan to share lists with the evaluation team only after households have consented to participate in the demonstration. Under this scenario, we will provide guidance on creating the household lists but will not be able to examine or manipulate the data before they are aggregated to the household level.
The evaluation requires a two-stage consent process. First, SFAs will obtain consent from households to participate in the demonstration and to release contact information to the grantee and evaluator. This stage must be completed before the next steps of the demonstration—random assignment and notification of selected households—can proceed. Second, the evaluation team will obtain consent from sampled households to be interviewed. For the POC year, three of the five grantees have indicated that they will use active consent for participating in data collection activities, although the actual consent process has not yet been finalized as of January 2011. Our goal is to implement a consent procedure in the POC year that will: (1) shed light the pros and cons of the active versus passive consent processes to help inform procedures in the full demonstration year; (2) be conducive to a high response rate; and (3) be as easy as is practical for SFAs and households.
In the first stage of the consent process, each SFA will send a letter to each eligible household explaining the demonstration and explaining what will happen if participants agree to participate. Under the active consent process proposed by the sites, the letter will include a waiver of confidentiality for release of personal information. This waiver will authorize release of data to the grantee (to be included in the grantee’s list for random assignment and for demonstration purposes, if the household is selected) and to the evaluator (for random assignment, analysis of sample frame characteristics, and for survey contacts, if sampled). As noted below, households selected for the POC year will be eligible for the following year if the grant is renewed, so the waiver will include the second year. The evaluation team will assist with this stage of the consent process, as needed, by providing grantees written materials introducing the evaluation and templates of consent letters. We will also work with grantees and SFAs to establish a process for tracking and documenting the rate of consent and the characteristics of non-consenting households.
For passive consent households, SFAs will send out letters to each of the households that says unless the household head contacts the SFA to opt out of the evaluation, his or her contact information will be released to the evaluator who will use the information to randomly assign
For each year, we will work with each site to determine the number of households to be contacted for the first stage of consent. The number of consenting households must be sufficient to assure that (1) the specified number of children can be assigned to receive SEBT for Children (2,500 in the POC year and 5,000 in the demonstration year), and (2) the treatment and control group survey samples will be large enough to complete the desired number of interviews. Where sites have significantly more than the desired number of households available, we will work with the sites to determine an unbiased, equitable, and efficient way to select the households to be contacted for the first stage of consent.
The second stage of the consent process will be conducted by the evaluator at the beginning of the baseline household survey. We will ask each household in the survey sample (selected from among the households who were selected to receive SEBT for Children and those who were not) to give verbal consent to participate in the evaluation. This consent process will inform respondents of how their information will be protected. We will ensure that the process is designed to carefully track and document households that do not consent in order to conduct a non-consent bias analysis later.
After completing the first stage of the consent process, each grantee will transmit a household file to the evaluators. From this file, we will randomly select approximately 960 households (that represent 2,500 eligible children; i.e., assuming approximately 2.6 eligible children per households based on analysis of SNDA-III data) to participate in the POC year, and we will provide this information to the grantees. From the households selected for the demonstration and the households that were not selected, we will draw an evaluation sample to achieve a final sample of 1,000 (500 from each group). The contact information for the evaluation sample will be loaded into the survey management system.
Exhibit B.1 depicts the sample. The widest circle represents the eligible population. The next circle depicts the households that have consented to participate in the demonstration. From those, 960 will be assigned benefits and the remaining will be in the control condition (i.e., they will not get the SEBT for Children benefits but will remain eligible for SFSP). The inner most circle represents the households that will complete the survey.
In POC sites that continue to be full demonstration sites in 2012, treatment group households selected in the POC year that remain in the SFA and certified for free/reduced-price meals will automatically be assigned to the treatment group. For all other households in the full demonstration year, in both the POC sites and the additional full demonstration grantees, the consent and random assignment process will be as described above.
Exhibit B.1. Evaluation Sample (numbers of households)
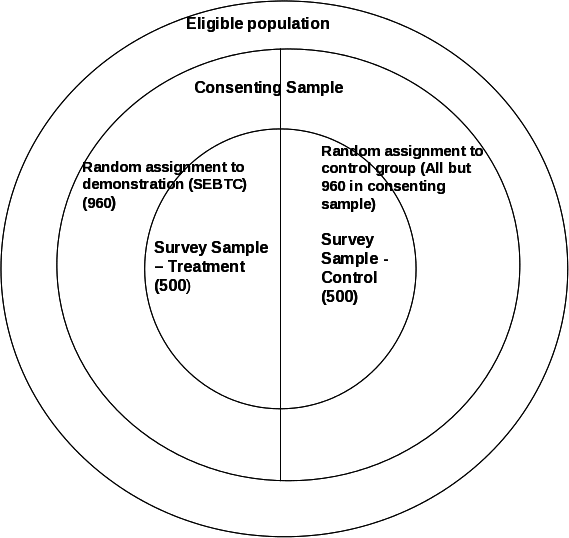
From the list of eligible consenting households provided by grantees, in each site the evaluator will randomly select approximately 960 households (representing 2,500 school-age children) in the POC year and 1,920 households in the demonstration year to be in the treatment group. The remainder of the eligible households in each year will be assigned to the control group. We will provide a data file indicating each household’s status to the grantee. Members of the treatment group will be provided benefits on an EBT card; members of the control group will not be offered benefits. Evaluation samples will be selected from the treatment and control groups. The grantees will notify households of their random assignment status.
The proportion of households assigned to the treatment and control groups will vary with the number of eligible children and households in each site. Grantees were asked to have a minimum number of 10,000 eligible children in the demonstration area. If we assume 11,000 children in each site and 2.6 eligible children in each eligible household (based on analysis of data from SNDA-III), we expect that there will be a approximately 4,231 eligible households in each site and benefits will be given to 962 households in 2011 and 1,923 households in 2012. If SFAs have only the minimum number of children certified for free- and reduced-price meals required by FNS, this approach would assign 23% of households to the treatment group in 2011 (the proof of concept [POC] year) and 45% in 2012 (the demonstration year). In both years, the remainder of the sample would be assigned to the control group. Exhibit B.2 summarizes the allocation.
Exhibit B.2: Illustration of the Percent Assigned to the Treatment Group in Each Site
Year |
Expected Population |
Treatment Group |
Control Group |
% Assigned to Treatment Group |
Number of Children |
||||
2011 (POC) |
11,000 |
2,500 |
8,500 |
23% |
2012 |
11,000 |
5,000 |
6,000 |
45% |
Number of Householdsa |
||||
2011 (POC) |
4,231 |
962 |
3,269 |
23% |
2012 |
4,231 |
1,923 |
2,308 |
45% |
a Assumes 2.6 eligible children per eligible household
The random assignment process must be carried out rigorously in each demonstration site. Whenever possible, the evaluator will directly implement the random assignment in each site, using de-identified data if necessary. When that is not possible (e.g., privacy concerns) we plan to closely supervise the implementation of random assignment by SFA or grantee staff.
Abt Associates will use the probability sampling procedures in SAS SURVEY SELECT to make the random assignment. The advantage of this approach is that the SAS program log serves as clear documentation of the correct implementation of the random assignment process. A similar approach can also be used if the eligible households are listed in a spreadsheet.
Random assignment is slightly more complicated for the POC sites that also operate in 2012. Many of the 2011 households will also be included in the sample frame for 2012. Our random assignment plan for 2012 needs to consider the outcome of random assignment in the previous year. Since some households will have moved and others will have changed certification status, we will construct a new sampling frame for 2012. Households in the 2012 sampling frame that were assigned to the treatment group in 2011 will be placed in a separate sampling stratum and will be automatically assigned to the treatment group in 2012. The remaining households will then be randomly assigned to the control group or to fill out the treatment group. The sample of eligible children will be nested within the sample households using a one-stage cluster sample design. That is, all eligible children in a household assigned to the treatment group will receive the treatment.
As part of the random assignment process, we will assess whether the data base used in each demonstration site contains useful stratification variables. An important stratification variable will be the number of eligible children in each household, as this determines the size of the benefit. We may also be able to stratify households on the basis of SNAP participation to ensure that the treatment and control samples have the same proportion of SNAP households. Other potential stratification variables include free versus reduced-price meals and an indicator of the children in the household being directly certified versus certified by application.
The Evaluation of the SEBT for Children will include 5 sites in the POC year (2 using a SNAP-hybird approach, one using a SNAP-based approach and 2 using WIC-based approaches) and 15 sites in the full demonstration year (approximately 9 using a SNAP-based approach and 6 using a WIC-based approach). In each site, we propose to collect data (i.e., survey completes) on 1,000 households in the POC year and 1,800 households in the full demonstration year. Thus, the total sample sizes will be 5,000 households in the POC year and 27,000 households in the full demonstration year. These samples would be split evenly between treatment and control groups (i.e., 500T/500C per site in the POC year, and 900T/900C in the full demonstration year).
Baseline data will be used for several purposes, including improving the precision of the impact estimates and estimating the difference in prevalence of very low food security among children between the school year and summer for members of the treatment group. In addition, the baseline survey may be crucial for improving our response rates in the summer, which is important for obtaining the necessary effective sample size and reducing the probability of non-response bias. Our approach assumes that we will field a baseline survey in both the POC year and in the demonstration year, although a limited data collection window in the POC year will mean that its major value will be for learning more about how it can improve response rates for the summer data collection.
The evaluation will also use a two-phase sampling plan. The sample design involves the division of the treatment and control group samples in each site into replicates or random subsamples. The sample will be released for data collection on a replicate-by-replicate controlled basis. Because the cost per telephone interview is much lower than the cost per field interview, all sample households in the first phase sample will be attempted by telephone. All telephone survey nonrespondent households in replicates released early (i.e., the second phase sample) will be eligible for field follow-up. The households in the second phase sample will be assigned higher base sampling weights than the households that are completed by telephone in the first phase sample. Replicates released later will not be eligible for field follow-up (even if they are not located by phone, no field follow-up will be attempted). This approach will help ensure that telephone nonrespondent households have sufficient time in the field to be completed. Because the replicates consist of random subsamples, this does not introduce sampling bias.
Such release of sample in replicates—with field follow-up for the second phase sample of nonrespondent households—is a cost-effective approach to achieving a high response rate despite the short field period, compared to: 1) a design that just uses telephone interviewing, or 2) a design that sends all telephone nonrespondent households to the field.
We propose in-person or field locating for nonrespondents to the telephone interview. As field locating is very resource intensive, we propose field locating only for a set of replicates that comprise around 45% of the sample. We will maximize the time we have for the field locating by selecting the first replicates for field locating. After 45% of the sample is released, we will not conduct field locating for any households in the subsequently released replicates. Hence, we will only release nonrespondent households for locating in the field early enough if there is enough time for the field locating to be successful. Given the compressed nature of the field work for this evaluation, this is an important advantage of this approach. Random sampling of nonrespondent households for the more expensive mode of data collection or locating is frequently used in surveys as a way to control costs. For example, the American Community Survey2 uses mail and telephone interviewing followed by field interviewing for a random subsample of nonrespondent households.
The optimal proportion of the sample eligible for field locating is given by the square-root of the ratio of the cost of an interview resulting from field locating, CF, to the cost of a telephone interview without field locating, CT. We estimate that the cost ratio is approximately 5, and hence the optimal allocation of sample eligible for field locating::
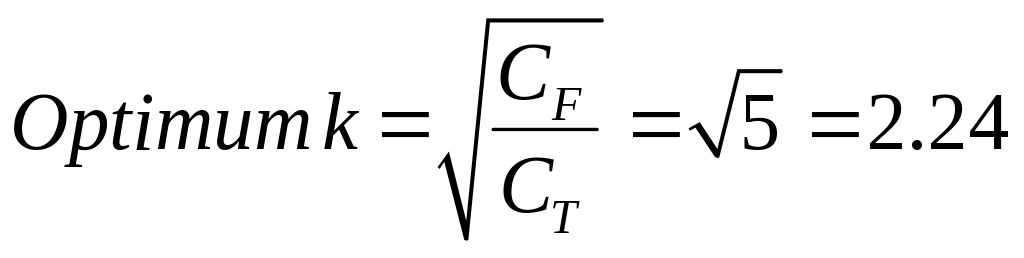
Thus, we should allocate a random sample of (1/2.24) = 45% of the telephone survey nonrespondent households for field locating.
We can illustrate the cost advantage of the proposed two-phase design, compared to a design that sends all telephone nonrespondent households to the field, using a sample size goal of 1,000 completed household interviews. We assume that the response rate to the telephone interviews without field locating will be approximately 50%; among the sample households that are sent to the field for locating the response rate will be approximately 40%. This yields an overall response rate of 70% (=50% + 50% x 40%; see below for an alternative motivation for this computation) for the sample that is eligible for field locating.
This implies that the sampling weights of the households interviewed through the field effort will receive a weight 2.24 times higher than the sampling weight of the respondents interviewed by phone. The resulting design effect from unequal weights, kh, from this subsampling equals:
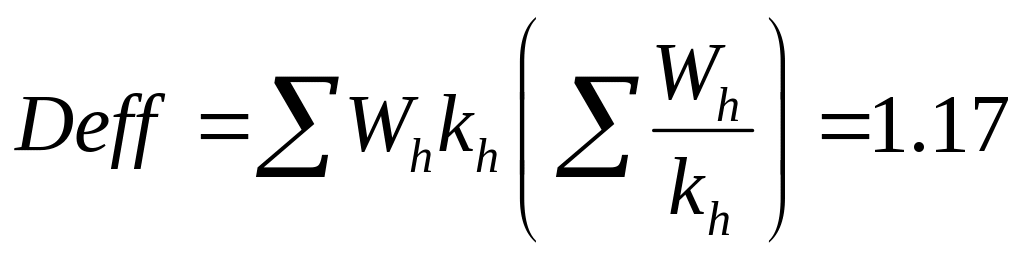
where W1 = 0.50, k1 = 1.0, W2 = 0.50, and k2 = 2.24. W1 is the proportion of the sample that is expected to be completed by telephone without field locating.
Using a hypothetical goal of an effective sample size of 1000 a simple random sample would cost 2142 units (based on the 1:5 phone:in-person cost ratio):
-
Cost Ratio
Cost Units
Drawn sample
1428
50% phone response
714
x1
714
40% in-person response from phone non-responders
286
x5
1428
Sample size
1000
2142
Effective Sample size
1000
Using the two phase design and keeping costs constant (at 2141), we can obtain a larger effective sample size of 1138:
-
Cost Ratio
Cost Units
Drawn sample
2260
50% phone response
1130
x1
1130
40% in-person response from phone non-responders
202
x5
1011
Sample size
1332
2141
Effective Sample size
1138
Therefore, the two-phase design yields a larger effective sample (i.e., incorporating the DEFF) than the one-phase sample.
As noted, using the AAPOR Standardized Response Rates for Two-Phase Samples we project a response rate of 70%. For the baseline survey, we expect that we can achieve a 50% response rate from telephone interviews and a 40% field response rate from the records that could not be completed over the telephone, due to the short time frame for that data collection. As explained below, these response rates for the two phases lead to our commitment to obtain a 70% overall response rate.
Calculating the response rate for a two-phase sampling design—while simultaneously heeding the AAPOR Standard Definitions response rate guidelines—is somewhat more complicated than for the usual single-phase sample design. We illustrate the calculation using the assumptions for the baseline survey (as discussed above) and a hypothetical target of 1,000 completed household interviews. As shown in the table, we will break the sample into three primary components: (1) first phase (telephone) respondents, (2) first-phase non-respondent households (2a) first-phase non-respondents not selected for second phase, and (3) first-phase non-respondents selected for the second phase. Exhibit B.3 shows the unweighted and weighted sample sizes for these three components and the breakdown of the second phase sample (3) between respondents (3a) and non-respondents (3b).
Exhibit B.3: Two-Phase Sampling Approach
Sample Component |
Sample Size |
Relative Sampling Weight |
Weighted Count |
1. First phase sample households interviewed by telephone |
847.5 |
1.0 |
847.5 |
2. First phase nonrespondent households @ 50% |
847.5 |
|
|
2a. First phase nonrespondent households not selected for second phase sample @55% of 2 |
468.5 |
0.0 |
0.0 |
3. First phase nonrespondent households selected for second phase sample @45% of 2 |
379.0 |
|
|
3a. Second phase sample households that complete the interview @40% of 3 |
152.0 |
2.24 |
340.5 |
3b. Second phase sample households that do not complete the interview @60% of 3 |
227.0 |
2.24 |
508.5 |
Total completed interviews (1 + 3a) |
999.5 |
|
|
Total sample size of households (1+2) |
1695.0 |
|
1696.5 |
A key aspect of calculating the response rate in a two-phase sample is the assignment of a weight of 0 to the nonrespondent households not selected for the second phase sample. The AAPOR response rate equals:
![]()
For the summer interviews we have committed to the same overall response rate of 70%, based on different assumptions. We expect to complete 55% of the summer interviews over the phone, because we are collecting updated contact data during the baseline interview. However, this information will be obtained only for the baseline respondents, and in general, we expect that it will be harder to reach sample households during the summer. Therefore, we expect a 33% response rate for the field interview subsample in the summer, again giving an overall AAPOR response rate of 70%.
There are two aspects to our assumptions about response rates and the resulting survey sample. In order to minimize the possibility of non-response bias, we will do everything we can to achieve as high a response rate as possible, given unknown information about the quality of the initial contact information and the level of the mobility of the households, both of which are likely to vary by grantee. However, because we have a very short data collection window, if we over-estimate the response rate, we will not be able to achieve the effective sample size necessary to achieve desired minimum detectable effects. While it is possible to correct for non-response bias—and we plan to do so no matter what the response rate is given that even a sample with an 80% response rate may be biased (e.g., Groves, 2006)—it is not possible to obtain a larger sample after the data collection window closes.
For this reason, we are estimating a more conservative response rate of 70% and are releasing sample that would make it possible to achieve the sample size if something critical happens at a site and we were only able to achieve a 60% response rate. In addition, we will do everything we can to achieve an 80% response rate. Our sense is that issues with response rate will be related to our inability to reach respondents, rather than respondent refusal to participate in the study. Some of the approaches that we are taking, as described in the data collection and remedial actions plans, include the following:
Including a large phone capacity in order to maximize the number of respondents we can contact in a short period of time;
Using customized call algorithms created by the contractor that have been developed as part of election-related surveys in order to reach respondents very quickly;
Using sophisticated advanced field location efforts created by the contractor;
Releasing appropriate sample to the field as quickly as possible according to protocols; and
Carefully monitoring response rates and increasing amount of field location hours when necessary
These actions are described more fully in Section B.2.3—Methods to Maximize response rates.
B.1.7 Analysis of Nonresponse Bias
Even with a response rate goal of 70-80%, unit nonresponse comprises 30-20% of the sample. There may not be a strong relationship between the response rate in a survey and the magnitude of nonresponse bias. For a survey that achieves a 60% response rate, some substantive variables may be subject to a small degree of nonresponse bias, while other variables in the same survey may be subject to more substantial nonresponse bias. The same statement may be made for a survey that achieves a higher response rate of 80%.
For this study, we can assess nonresponse bias and make adjustments for both the baseline survey and the follow-up survey. Our plan is to create a sampling frame of households in each site that includes auxiliary variables such as number and grade level of school children, SNAP participation, free versus reduced-price school meal certification, and disability status. The auxiliary sampling frame variables will be available for both the respondent and nonrespondent baseline sample households, and we can compare respondents and nonrespondents using the sampling frame variables separately for sample households assigned to the treatment and control groups. This analysis may identify auxiliary variables to use in post-stratification weighting adjustments to reduce nonresponse bias.
Another key aspect of the baseline survey is the two-phase data collection approach. We can compare the interviews completed by telephone without field locating with those completed after field locating. To the extent the households completed in the field are a reasonable proxy for nonrespondent households, the comparison will serve as a good assessment of nonresponse bias for a wide range of substantive variables.
The nonresponse bias analysis planned for the follow-up survey will use the two approaches discussed above for the baseline survey. We expect to have baseline survey data for a large portion of the follow-up sample, which will allow us to examine the use of response propensity modeling to assess and potentially adjust for unit nonresponse in the follow-up sample. This nonresponse bias analysis should identify statistically significant predictor variables in a logistic regression model of response in the follow-up sample. The predicted probabilities from the model can then be used to form response propensity weighting cells within each demonstration site.
B.2 Procedures for the Collection of Information
Procedures for the collection of information addressed below include:
Statistical methodology for stratification and sample selection;
Estimation procedure;
Degree of accuracy needed for the purpose described in the justification;
Unusual problems requiring specialized sampling procedures; and
Any use of periodic (less frequent than annual) data collection cycles to reduce burden.
B.2.1 Statistical Methodology for Stratification and Sample Selection
As noted above, we may stratify our sample to improve precision. Such stratification has some small implications for standard errors. An important stratification variable will be the number of eligible children in each household, as this determines the size of the benefit. In addition we may also wish to stratify on the receipt of SNAP benefits,
In this section, we present our plan for estimating the impact of receiving SEBT for Children benefits on food security, nutritional outcomes and program participation. We begin with a discussion of process study analysis and descriptive statistics, before turning to the estimation of the impact of SEBT for Children-benefits. Our discussion of impact begins with conventional models in a site, pooled, and in subgroups. As described more fully in Section B.2.3, we note in this section that our MDDs for subgroups are moderate in size. We therefore also describe models that pool across subgroups and thereby allow us “borrow strength” across the subgroups.
Process Analysis
The analysis of SEBT for Children demonstration implementation will include three main components: (1) a description of the implementation of the demonstrations at each site; (2) comparisons and synthesis of implementation narratives across sites; and (3) an assessment of the feasibility, the challenges faced, and the lessons learned. These analyses will use data from stakeholder interviews and from demonstration documents, including periodic reports from the grantees, as well as administrative data files and household survey responses. Below, we describe the full analysis for each of these components.
Description of the Demonstration Implementation
We will begin by compiling interview data for each site into a database to facilitate comparisons across sites and rapid reporting. This process will be ongoing across the waves of interviews, so that discrepancies in data can be identified and resolved through follow-up.
Once we have analyzed and integrated the interview data by site, we will then review similarities and differences across sites, both within the three models (the WIC-based approach, the SNAP-based approach, and the SNAP-hybrid approach) and across all sites. This review will allow us to describe the most common patterns of implementation and the key differences across sites. Key dimensions will include: project organization, the design of the SEBT for Children program, household consent and recruiting process, card issuance and training, stakeholder outreach and training, customer support, and project schedule.
We will incorporate data from administrative reports into a database designed to facilitate tabulations both within sites over time and across sites. We will produce summary tables highlighting key contrasts in implementation practices across sites (such as different approaches to outreach and consent) and supporting tables that will be included in appendices to reports. The tables will also include characteristics of the project sites, including SFAs, schools, and retailers (e.g., measures of access/food deserts), as well as cross-tabulations of these characteristics with key implementation strategies. From this analysis and synthesis, we will address the core research questions of the process study, including the operational and technical feasibility of the program, the circumstances of site/population characteristics associated with implementation success or problems, with particular attention to any unanticipated consequences of events and decisions and to lessons learned (especially in the POC year). This phase of analysis will inform the interpretation of impact findings.
Feasibility of Future Implementation
We will use the qualitative findings and quantitative data on program operations to assess the feasibility of future implementation of SEBT for Children, and to formulate options and recommendations for improving its feasibility and efficiency. This analysis will address the key feasibility issues:
Is SEBT for Children technically feasible for all of the organizations involved in implementation and operations: State agencies, SFAs, EBT vendor, retailers, local SNAP/WIC offices, and local organizations?
What are the technical requirements for success?
Is SEBT for Children operationally feasible for all of the organizations involved? What are the greatest challenges and risks?
What are the differences in feasibility between the SNAP and WIC approaches to SEBT for Children? What are the implications of these differences for policy?
How can the feasibility of SEBT for Children using the SNAP systems and WIC systems be improved?
Both technical and operational feasibility are critical to the success of SEBT for Children. Technical challenges for the grantees include constructing a database of eligible households, modifying information systems (SFA, State, and EBT vendor), and managing participant data and benefit funds. Operational challenges include notifying households and retailers, issuing cards and personal identification numbers (PINs), and providing training and customer support. Finally, SEBT for Children will be implemented on top of existing program operations. The interaction of the new program with existing programs poses another operational challenge, particularly for SFAs and local SNAP or WIC offices. Key informants will likely have a variety of suggestions for improvement, based on both their successful decisions and the ones that were less successful. Comparisons across sites and the longitudinal perspective provided by grantees participating in both the POC and the full demonstration years will be particularly useful in addressing these questions.
Using Lessons from Proof of Concept Year to Inform Full Demonstration Year
Lessons learned about the ability of sites to administer effectively either the SNAP-, the SNAP-hybrid, or WIC-based models will be provided to FNS to inform its decision about whether to allow the POC sites to continue on to become full demonstration sites. In addition, insights gained by the evaluation staff from understanding the strengths and weaknesses of implementation of the SEBT and the associated evaluation tasks will help FNS to shape the RFA for demonstration sites in 2012. For example, we may provide FNS with advice based on our assessment of costs and benefits of the sites obtaining active versus passive consent for participation in the Summer EBT for Children program. We also may provide FNS with feedback on such things as model training practices for the use of the Summer EBT for Children using the WIC model.
Descriptive Analysis
Both for the 5 POC sites and then for the 15 full demonstration sites, prior to estimating multivariate statistical models for the impact of the program, we will present several simple tables to provide an overview of the distribution of our sample across program sites, sample characteristics and the study’s key outcomes, including rates of food security and children’s nutritional status. Separate tables will be provided for baseline and summer data.
Descriptive analyses fulfill three purposes. First, the descriptive analyses help us to understand the study sample and the study sites. Second, the analysis allows us to verify that randomization was properly implemented.
Finally and perhaps most importantly, these descriptive analyses provide an answer to the key descriptive question: How big is the problem? The actual difference in levels of food security among school children between the school year and the summer months is unknown. The premise is that food security declines sharply from the school year (when children have access to SBP and NSLP) to the summer (when children have access only to the smaller SFSP). However, available evidence (e.g., Nord and Romig 2006) does not apply specifically to the SEBT for Children sites and is no longer current (VLFS is likely to be much more common in the current deep recession).
We now discuss each of these uses of descriptive analysis, beginning with prevalence of VLFS.
Determining Prevalence of Very Low Food Security and Other Outcomes.
Given the limited data on school year/summer changes in food security and other nutritional outcomes, we will begin our analysis by estimating the prevalence of VLFS among children, other food security measures, and nutritional status measures in the selected sites among children certified for free or reduced-price meals. We will examine how outcome measures vary with observable characteristics.
For prevalence estimates, we will use both treatment group and control group observations for spring measurements, but only control group observations for summer and spring/summer change measurements. We note, however, that despite our large samples sizes, VLFS is a rare event, so our estimates of prevalence will have considerable sampling variability.
We also note that our prevalence estimates will be for households providing consent, and that it appears that three of five POC sites will require active consent. In those three sites, our prevalence estimates will be limited to the households that volunteer to participate in the study and therefore will not reflect the actual prevalence of households with children who are eligible for SEBT for Children.
Understanding Sample Distribution Across Sites
Beyond distributions of these key outcomes, we will also tabulate the distribution of baseline demographic characteristics of the study population and how they vary across the sites. Characteristics of interest include gender, age, race/ethnicity, household size, and program participation. We will also tabulate outcomes of interest. The self-reported outcomes include food insecurity among children (low and very low), food expenditures, consumption of specific healthful foods, awareness and views regarding the SFSP, participation in other programs, and strategies to obtain food during the summer.
We will tabulate these characteristics for the 5 POC sites in 2011 and for the 15 demonstration sites in 2012. We will tabulate them by site, in addition to aggregating them for the SNAP-based sites and for the WIC-based sites, and finally across all of the sites (regardless of program approach). We will disaggregate treatment and control.
In addition, for the treatment group we will report measures related to SEBT for Children participation derived from surveys and EBT system data. These measures include acceptance and use of SEBT for Children, distribution of benefits within the household, foods on which the benefit was spent, changes in food supply over the summer, satisfaction with the program, and issues related to participating in the program.
Checking Randomization
Descriptive statistics also serve to gauge the success of the random assignment process. When properly implemented, random assignment baseline characteristics of the treatment and control groups should differ only by chance. We will conduct those tests for the 5 pilot sites in Year 1 and the 15 demonstration sites in Year 2, at the individual site level, aggregating by treatment model, and for all sites combined. More statistically significant differences between program and control group than expected by chance alone could indicate that there are issues with the randomization.
We will begin by comparing treatment and control means or distributions for each baseline variable using conventional (i.e., uncorrected for multiple comparisons) statistical tests for equality of means. Given the large number of variables to be compared, we would expect that using uncorrected p-values some differences will be “statistically significant”. We will scan these results for any apparent patterns.
We will then conduct a formal test of the hypothesis that key characteristics are jointly identical across treatment and control groups. The appropriate test is an F-test of the hypothesis that all of the differences are simultaneously zero. That joint test must account for the correlation of the outcomes and the complex nature of the data (including clustering and unequal weights). SAS PROC SURVEYMEANS will perform the required tests.
Assuming that randomization is correctly implemented in samples as large as these, we do not expect meaningful treatment/control differences in background characteristics. Differences will remain, however, just by chance. The regression estimators discussed below will control for any random imbalances between the treatment and control samples.
Implications of the Evaluation Sample for Interpreting Impact Analysis
Random assignment estimates the average difference between treatment and control observations for the sample of households that are randomly assigned. In the SEBT for Children demonstration, the sample would probably differ substantially between sites by whether households in demonstration areas are asked for either active or passive consent. If SFAs require passive consent for the demonstration (i.e., household heads need to opt out of the demonstration) and then active consent for the evaluation (i.e., household heads would be asked when contacted to participate in the evaluation), we would expect relatively few families to refuse to give passive consent (i.e., actively opt out of the demonstration). We would therefore randomize nearly the entire eligible population, including those that may or may not take up the benefit. In this case, the evaluation could plausibly be viewed as estimating the impact of SEBT for Children for all children who are eligible for the benefit within that demonstration area. In addition, any estimates of the prevalence of food insecurity or other outcomes would be for the eligible population in that demonstration. For example, if we find that during the summer the 7% of the control group has very low food security among children (VLFS-C), but only 6% of the treatment group has VLFS-C, we can legitimately conclude that applying the program more broadly will lower VLFS-C by 1 percentage point (among households offered the program; in sites similar to the sites in our study).
As described in the grant applications, three of the five POC sites will require some form of active consent both to participate in the demonstration and in the evaluation. It seems likely that those providing active consent and therefore being randomized will be a substantially smaller group than if a site only required passive consent. Some of the factors that will determine this include the clarity of the information provided, the ease of the consent process, the extent of outreach to selected households, and the desirability of the benefit. It may be the case that a relatively small fraction of eligible households return the forms necessary for active consent. If so, those who consent are unlikely to be a random sample of all eligible families. They may be families with higher literacy levels; it is also possible that they will be families with higher levels of food insecurity. The relevance of the impacts of SEBT for Children for households providing active consent will not necessarily be applicable for SEBT for Children implemented as a regular program, unless the program, when fully implemented, requires the same active consent process that is being used for the demonstration.
Our goal is to estimate the impact of SEBT for Children on all eligible children—including those who provide active consent and those that do not. To estimate that impact for a demonstration that requires active consent, note that the program can only have an impact on those who provide such consent. For those who do not provide active consent, the impact of the program must be zero. Under these assumptions the impact of the program on the entire eligible population can be estimated as the product of the fraction of the eligible children providing consent and the impact in the population providing consent. Thus, for example if in the consenting population, we estimate that the VLFS rate is 11% in the control group (VLFS households are more likely to consent) and 8% in the treatment group (the program makes a large difference), but only a third of the children consent, then the impact on all eligible children is 1 percentage point (i.e., [11-8]*[1/3]). We will know the (i) aggregate data on how many children were in households that did not provide consent and (ii) complete contact information for those households that did provide consent. From this information, we can compute the fraction of children providing consent. From the random assignment evaluation on those who do provide consent, we can estimate the impact in the population providing consent. If some of the households not consenting in the demonstration would consent for the broadly rolled-out program, the estimates using this approach will be a lower bound; i.e., the true impacts will be larger. Below, we describe some simulations we will do to understand the range of plausible impacts for a broadly implemented program that required only passive consent (vs. active consent for most of the demonstration sites).
However, it seems likely that the consent process for a broadly implemented program would differ from the consent used in the demonstration. At the very least, in the demonstration, consent involves both the benefit and the evaluation; in a broadly implemented program, consent would only be for the benefit. In addition, it seems likely that publicity for a broadly rolled out program would be better than for the demonstration. Such publicity would likely lead to higher consent rates. As long as active consent (i.e., filling out a form to get the benefit, perhaps providing a spring address to which to mail the EBT card) is required for the broadly implemented program, it seems plausible that any such impacts would be second order.
If the broadly implemented program would require a different consent process, then the situation is more problematic. Our experiment only estimates the impact for the population that provides consent. It seems plausible that impacts in the population that does not provide consent would be different than impacts in the population that provides consent. The ideal solution to this problem is to induce the SFAs to implement a consent process for the demonstration that is as close as possible to the consent process that would be used in the broadly rolled out program.
In as much as there is a difference between the consent process for the demonstration and the consent process for the fully rolled out program, we could explore non-experimental methods to develop extrapolations of the program's likely impacts with a different consent process. The most promising way to extrapolate is to compute impacts on the experimental data reweighted so that the experimental data align with the observed characteristics of eligible population (rather than of the consenting population).
The weights would be based on aggregate data that we would have both for those who do and for those who do not consent. We are currently working with the SFAs to better understand what information is likely to be available. Variables that seem likely to be available include: gender, race/ethnicity, grade, ESL status, Free/Reduced lunch status, number of eligible children in household. This information would be most useful if we had individual level data as opposed to aggregate data. We will work with SFAs to get such data, stripped of identifiers, from non-consenting households.
Any such analysis is outside of the experimental framework. We propose to treat such analyses as a sensitivity analysis. We would explore how the results vary as we adjust the weights from “Consenting Children Only” to “Consenting Children plus 25% of the Nonconsenting Children,” to “Consenting Children plus 50% of Nonconsenting Children,” to “Consenting Children plus 75% of Nonconsenting Children,” to finally “Consenting Children plus All Nonconsenting Children.”
Estimating Models
This section describes the statistical models to be used to estimate the impact of SEBT for Children. These models apply to all variables measured in both the treatment and control groups. We will begin by applying these models to VLFS as measured in the summer. We will then apply these models to broader measures of food insecurity (LFS or VLFS, rather than VLFS) and a few important measures of nutritional status (e.g., fruit and vegetable consumption, eating breakfast). Finally, we will apply these models to other outcomes (awareness of the SFSP, food expenditures, participation in other programs, strategies to obtain food over the summer). Where we have measures both in the spring and the summer, we will also apply these models both using summer outcomes as the outcome (with spring outcomes as regression controls) and also using the change between spring and summer as the outcome (sometimes with spring outcomes as a control).
In principle, these models can be applied to either the POC year (with samples of approximately 5,000) or to the Demonstration year (with samples of approximately, 27,000). At the end of this section, we discuss our strategy in each year.
Within-Site Estimates: Simple Differences
Within a specific site, the random assignment procedure should ensure that there are no systematic differences between research groups other than the presence of the program. Since that the key outcome for this study, very low food security, is binary, we will estimate impacts using a logit model. The logit models explicitly account for the necessarily non-linear relation between covariates and the probability of the outcomes. For continuous outcomes, we will use linear regression. In the discussion that follows, we only present the logistic regression specification. The corresponding linear regression specification should be clear from the specification for the logistic regression case (i.e., replace the index with the continuous outcome).
The logit model for pooled impacts in a single site is:
(1) ![]()
where y=1 if I>0; otherwise y=0.; y is the outcome of interest for individual i in household h in site s. T is an indicator variable for treatment (that is, 1 for treated households and 0 for control households; with s and h subscripts, but no i subscript—randomization is at the household level). is the impact of the program in site s (here with a “1” subscript, corresponding to the first in the sequence of estimators), X is a vector of characteristics observed at baseline that are correlated with the outcome, is the corresponding vector of regression coefficients, and is a regression residual.
With random assignment, simple treatment/control comparisons are unbiased and consistent. No covariates are needed. Nevertheless, estimation using regression (logistic regression for binary outcomes, linear regression for continuous outcomes) yields more precise estimates of the policy impact. This additional precision is gained because the included covariates shrink the residual variance. As long as the covariates are measured before random assignment, they can not be correlated with treatment status (i.e., the outcome of random assignment) and they will therefore not induce bias into the estimates of the treatment effect. Below we discuss the particular covariates, X.
Under the assumption that has the extreme value distribution, this construction yields the conventional logit model. For expositional clarity, in the discussion that follows, we only state the index, I; the transformation to the binary outcomes remains as above.
We will handle any missing data using “hot deck” imputation. Adding additional “noise” through multiple imputation is neither necessary nor appropriate in the random assignment context.
Pooled Site Estimates by Program Type
The discussion above focuses on analysis for a single site. Our sample sizes will allow us to detect only relatively large impacts within a given site. Pooling across sites, our sample sizes have the ability to detect much smaller impacts. The natural strategy for pooling is within program models: SNAP-based or WIC-based. We can adapt a logistic regression model shown in Equation (1) to pooled data by including site fixed effects, , and extending the sample to all individuals in a site with a given program model. We then estimate, not one regression for each site, but instead two regressions – one for the SNAP-based sites and one for the WIC-based sites, or even one model pooling over all sites:
(2) ![]()
The site fixed effects are simply indicator variables for each site and account for all differences (observed and unobserved) across sites that do not vary over time. In these specifications, yields the average impact of the program across all sites with a given program model (SNAP-based or WIC-based) or overall.
Estimates from these two models (one for SNAP-based and one for WIC-based approaches) would be independent. It is therefore straightforward to construct statistical tests of whether one particular approach—SNAP-based or WIC-based—has larger impacts. Thus, this analysis allows us to estimate how impacts on outcomes of interest vary by type of intervention. We will estimate these models separately for the 5 pilot sites in 2011, and the 15 demonstration sites in 2012. We will, however, not use these models to compare impacts across years. Other models discussed below are more appropriate for those comparisons.
Examining Variations in Program Impacts with Site Characteristics
FNS is also interested in learning whether observed impacts vary by key site characteristics, including the type of intervention, the value of the benefit, cost, location, as well as by program year (POC/2011, demonstration/2012, and option/2013 if funded). Finally, the demonstration program is in addition to the conventional Summer Food Service Program (SFSP). We might expect the demonstration to have a smaller impact where the conventional SFSP had more reach. Estimating impacts according to these subgroups will require additional model specifications.
We approach the specification of such models with insights from the ANOVA/Analysis of Variance and Hierarchical Linear Model (HLM) (Raudenbusch and Bryk 2002) literatures. Specifically, we will use models of the form:
(3) ![]()
where model (3) differs from model (2) in several ways. First, we now pool all of the observations across all of the sites in estimation (vs. Model (2) which only included the observations with a given treatment model, SNAP or WIC). Second, we now include regressors to capture observable site variation, Z (the second term, with corresponding regression coefficients, ) instead of the site-specific fixed effect. Third, we now include a site specific random effect, ν, that should now be interpreted as variation across sites in impact above and beyond what is related to the included observable characteristics, Z.
This approach has two advantages. First, it allows us to control for multiple site characteristics simultaneously. While 15 is a large number of sites, it is not a large number of observations with which to explore the impact of site specific characteristics. This regression specification uses the limited data efficiently, and it easily supports statistical tests for whether impacts vary with site characteristics. The appropriate test is the equivalent of a t-test on the terms in with standard errors adjusted appropriately (as discussed below).
We plan to use a pretest approach to choosing site variables. In this pretest approach, we begin with a list of site characteristics to include in an initial model, drop the terms that are not statistically significant at 10%, re-estimate yielding a final model, report both the preliminary and final results, and use the final model to generate estimates of impacts by site characteristics, standard errors for those estimates, and tests for whether there is variation in impacts with site characteristics.
The simplest form of this model specifies Z with only a dummy variable for sites using the WIC approach (that is, 0 if the site is using the SNAP-based approach and 1 if using the WIC-based approach). Thus, measures the pooled impact of the program and measures the differential impact of the WIC-based model over the SNAP-based model. Having estimated this model, we will test for equal impacts across SNAP-approach sites and WIC-approach sites with a t-test for the corresponding coefficient. If we reject equality, then we will estimate the impact for SNAP-type sites with and the impact of WIC-approach sites with .
Another important generalization of this model is to include a continuous proxy for the strength of the conventional SFSP. We will use average daily participation in SFSP as a percentage of children certified for free/reduced-price meals as our measure of market penetration. We will collect meal counts for SFSP and the number of operating days during our contacts with SFSP sponsors and State agencies.
We will also estimate generalizations of this model that include interactions of Z and X (e.g., terms like WICXsihs). Such terms allow the impact of covariates to vary across the two treatment models. To determine which covariates will vary in this way, we will again use a pre-test strategy in which we run the model allowing everything to vary across the two groups. Then we will drop terms in X that do not differ across the two groups, and use that model to estimate impacts.
Control Variables for the Analysis
Control variables are not necessary to generate unbiased and consistent estimates of overall program impact. (Covariates are needed to estimate subgroup impacts; we discuss subgroup issues below.) We nevertheless plan to include covariates because doing so improves the precision of the estimates. We will select the control variables to be included in regression models from the available baseline characteristics. These include both time-fixed characteristics and time-variable characteristics which are measured in the spring immediately prior to the summer program. Because they will have the most impact on precision of the estimated impacts, we are most interested in variables that are likely to be correlated with outcomes, especially the key outcome of very low food security. We expect the most relevant variables to fall into the following categories:
Baseline levels of food security: The key outcome of interest, the prevalence of very low food security among children, is likely to have at least some persistence (households that experience food insecurity during the school year are more likely to do so during the summer); this will be included as a dummy variable. This variable is likely to have higher explanatory power than most other variables. We will also consider including a dummy variable for low food security.
Other household characteristics: Household characteristics including size, composition, location (urban versus rural; though this is likely to be strongly correlated with site and therefore difficult to estimate), income and the characteristics of the household head (e.g. education, marital status, race, and Hispanic origin) could all plausibly be correlated with the level of household food security. Baseline levels of participation in other programs (e.g., SNAP and WIC), food expenditures, and use of emergency food services could also be relevant. VLFS is related to deep poverty. We will therefore explore the predictive power of proxies for deep poverty (e.g., dummy variables for low income, use of food pantries, participation in transfer programs). These characteristics will be obtained from the household surveys and may also be useful dimensions for subgroup analyses.
Child-level characteristics: Some outcomes vary at the child level. For these models, some baseline characteristics of the individual child could be relevant for outcomes and may again be useful for subgroup analyses. These characteristics include age, grade, gender, race, ethnicity, NSLP and SBP participation, after school meal/snack program and backpack food program participation.
Previous experience suggests that once we have measured and controlled for the outcome of interest at baseline, the incremental contribution of other covariates is likely to be small. This empirical pattern leads to more parsimonious models when a baseline measure of the outcome is available.
Subgroup Analysis
FNS is interested in the variation of impacts across such subgroups as household participation in SNAP, recipient characteristics (e.g., age, gender, grade level), participation in SFSP, WIC, and NSLP/SBP, and baseline levels of food security and nutrition status. Since our within-site sample sizes are likely to be too small to detect all but very large differences between subgroups, we will pool data across sites for subgroup analysis. The discussion of MDDs (see below) makes clear, even after pooling our ability to detect differential subgroup impacts will be limited.
Our basic approach is to estimate differential impacts across subgroups using pooled data—across sites and across program models. These models will be in the form of Equation (4) below, where Q is an indicator variable identifying a particular subgroup (that is, 1 for members of the subgroup and 0 for non-members). We will explore indicators at the household level (e.g. SNAP participants) and at the child level (e.g. males).
(4) ![]()
T is a treatment indicator, X is a vector of baseline individual or household characteristics, Z is a vector of site characteristics, µ is a site fixed effect, is a site random effect, and ε is a regression residual. In this specification, gives the pooled impact and gives the differential impact for the relative subgroup given by indicator Q (e.g. SNAP participants compared to non-participants). A test of the hypothesis that verifies whether there is indeed a differential impact for the given subgroup.
Our tentative plan is to estimate this model on the fully pooled data—across both treatment models (SNAP-based and WIC-based) and across all program years. We do this to boost our power for estimating subgroup impacts. Our models allow for a difference in the pooled impact between the two treatments. Given that we have allowed for this overall difference in the pooled impacts, allowing for common impacts of subgroups seems plausible and a reasonable way to gain additional power for subgroup analyses of most importance. Finally, we can and will test whether subgroup impacts vary by site.
Our primary analysis plan is to stratify based on characteristics known at baseline. Such estimates are supported by the random assignment strategy. FNS’s objectives also include analyses stratifying on outcomes only revealed after baseline (e.g., use of SEBT for Children benefits, household food expenditures and shopping patterns in summer, and where children ate meals during summer months). We will report results of similar models with these variables as defining subgroups. We note, however, that such analyses should be interpreted with caution because they stratify on outcomes that may well have been affected by the intervention, and therefore results are outside the random assignment design.
Comparability Across Sites, Demonstration Models and Years
To the extent possible, FNS is interested in comparisons of the program’s impact across sites, treatment models (SNAP-based or WIC-based) and years (2011 and 2012). Model (2) and Model (3) that were described above will support these analyses. More detail follows below.
Across Sites
As discussed earlier, we plan to present separate impact estimates for each site in addition to pooled estimates across sites. However, due to the relatively small sample size in any single site, the site-specific impact estimates are likely to be fairly imprecise, allowing the detection only of large impacts (see the power analysis below). Equation (3) is general enough to include site characteristics beyond SNAP-based and WIC-based models. We will conduct analyses of urban/rural differences, acknowledging that with 15 sites total (9 SNAP-based sites and 6 WIC-based sites), our ability to explain variation in our site-specific estimates will be limited. Of more promise is to use Equation (4) and its modeling of the variation in impacts with individual characteristics to understand sources of variation in impacts across sites (see Bloom et al. 2003, for a similar decomposition of cross-site impacts). Following standard multi-level modeling approaches (as in Bloom et al. 2003), we can test whether there is any evidence of heterogeneity in impact across sites—even if we cannot observe what it is correlated with.
Across Program Models
Estimates using the full pooled sample give us the best chance of identifying differences in impacts across the two program models. We will also attempt to identify these differences for particular subgroups of interest, although such estimates will have lower statistical power (see below).
Across Years
This evaluation will focus on two years of the program: the proof-of-concept demonstration in summer 2011 and the full demonstration in summer 2012. As noted earlier, using Equation (3) or Equation (4), we will be able to conduct a formal test of the hypothesis that the impact of the program on very low food security was identical in these two years, both for the program overall and for the two program models. To do so, we will pool observations across years and include a term in Z (the site level characteristics) for program year. We note that with only five sites in the pilot year (and a smaller number of observations per site), estimates of impact for the pilot year will be relatively imprecise. As a result, we will only be able to detect relatively large differences in impacts between the pilot year and the demonstration year. (See the power analysis for sample calculations).
Computing Appropriate Standard Errors
For each of these models, we need to compute appropriate standard errors that consider the following issues:
Stratification: To improve precision, we may stratify our sample. Such stratification has some, but usually small, implications for standard errors.
Weighting: Our two-phase fielding scheme requires unequal design weights. Unequal numbers of children within households will also induce unequal weights. In addition, there will be survey non-response, and we will construct non-response weights to account for this. We will have some list information which will support better non-response models than the standard survey sampling case (e.g., Random Digit Dial). The more such list information we have, the better will be our non-response weights. We will discuss with each site what such list information will be available. Candidate variables might include: gender, age, grade level, free/reduced-priced status, method of certification, and race/ethnicity; some may only be available at the site level. We will use information from the spring survey to create weights to for households that respond to the spring survey, but not the summer survey. We discuss the construction of the weights and the corresponding non-response analysis above. Our analysis will include these weights.
Clustering: The observations will be clustered at the site level. We will include site dummy variables, but our models should allow for clustering in impacts by site (above and beyond any including covariates—at the site or individual level). For outcomes at the child level, children will be clustered in families, but we will have outcomes only for a focal child, so impact estimates will not have to be corrected for clustering.)
Heteroscedasticity: Conditional heteroscedasticity also seems possible and will be controlled for using a robust variance estimator.
Panel Data: FNS’s site selection plan assumes that the five POC sites in 2011 will continue as demonstration sites in 2012 if they are successful. While the POC sites will be asked for a new sample frame (i.e., all children who are certified for free and reduced-price meals in the 2011/12 school year), there is likely to be overlap between the two years. Our randomization plan calls for continuing in the treatment group in 2012 anyone who was in the treatment group in 2011 and who remains eligible. Thus, some households will be in the sample in both years. This induces some non-independence across 2011 and 2012. Any models that combine observations from 2011 and 2012 will need to consider this panel aspect of the data. We note, however, that the impact is unlikely to be large. First, only a third of the sites will overlap. Second, the larger sample in 2012 vs. 2011, migration, and change in eligibility all imply that only some of the sample will overlap in the five POC sites. Finally, the correlation in very low food security over time appears to be weak.3
To use logistic regressions, we need software that can handle three aspects of our design: (i) logistic regression; (ii) multi-level models; and (iii) the analytic weights that will be used to adjust for the two-phase field work and non-response adjustments. The Stata 11 software package’s “gllamm” (generalized linear latent and mixed models) command appears to satisfy all of these requirements and we are currently using it on several other evaluations. It also appears that HLM 6 (Hierarchical Linear and Nonlinear Modeling) software package published by Scientific Software International would also support the required estimation. We will use HLM as a backup if we encounter problems with Stata.
Multiple Comparisons
FNS is interested in multiple outcomes (very low food security, low food security, multiple nutritional outcomes) and multiple subgroups defined at the site and individual levels (at the site level: SNAP vs. WIC, urban vs. rural; at the individual level: on SNAP during the school year vs. not on SNAP, grade level, program participation). We plan to report results—stratified and parametric—for each of the outcomes and subgroups as requested by FNS. We will also report conventional standard errors for those outcomes and subgroups. For subgroups, we will also report tests for differences in impact.
Note, however, that the power analyses described below and the conventional standard errors that we will report are strictly appropriate only for a given single outcome or subgroup. Given the large number of outcomes and subgroups of interest, the power analysis and MDDs must be considered in terms of the entire set of outcomes rather than for any individual outcome (Schochet 2008, 2009).
Estimating impacts on a large number of outcomes and using the inappropriate conventional (i.e., not corrected for multiple comparisons) statistical tests is likely to result in some estimates appearing to be statistically significant just by chance. Mistaken inferences will then occur if one heeds only significant outcomes while ignoring insignificant outcomes. Because statistical tests assume that only one outcome is being considered, the error is not with the test itself but rather with how the test results are used. One approach to this problem is to report all of the results, while correcting the standard errors for multiple comparisons. However, even modern approaches to correcting for multiple comparisons substantially increase the MDDs, and the result is that few (if any) impacts may be significant (see Schochet 2008, 2009).
For this evaluation, we propose to take an alternative approach: to specify—before seeing the results—which outcomes are of primary interest. Such analyses are termed “confirmatory” and the reported statistical tests are corrected for multiple comparisons; other analyses are termed “exploratory” and the reported statistical tests are not corrected for multiple comparisons and are therefore interpreted with caution. For this study, we propose to treat very low food security among children as the primary outcome and the corresponding statistical tests as confirmatory. We propose to treat all other outcomes as exploratory, preserving the smallest possible MDD for the confirmatory outcome.
Under our proposed approach, if we find a statistically significant impact on food security among children for the pooled analysis, we will report that there are positive impacts of SEBT for Children; if not, we will report that the study found no evidence of positive impacts. This is our recommended reporting strategy, regardless of whether considering other outcomes would indicate that the program had positive impacts.
FNS requests a minimum of three analyses of impacts on subgroups, specifying SNAP participation at baseline as one subgroup. We will treat the estimation of a differential impact for this subgroup analysis (SNAP participation) as confirmatory. We will treat the other two subgroup analyses (income and gender) as exploratory.
In practice, this means that our primary, confirmatory, estimates will pool all sites (across both program models), but include no site characteristics (i.e., Model 2). Our analysis of sub-groups will use Model (4), but include only one individual-level characteristic, SNAP participation. In this model, we will test for differential impact by SNAP participation status. We will also estimate and report estimates from models with other site specific characteristics and other subgroups, but we will treat these results as exploratory.
POC Year (2011) vs. Demonstration Year (2012)
We view the POC year as primarily a chance to pilot test the operational issues with SEBT for Children. Given that we will have some data, it is our plan to run all of the analyses planned for the Demonstration year data on the POC year data. This will give us a chance to test the models and identify any issues. It is, however, crucial to note that the samples in the POC year are much smaller than the samples in the Demonstration year—5,000 vs. 27,000. VLFS is rare (under 10 percent prevalence), so impacts on VLFS must be small. Thus, detecting impacts on VLFS during the POC year will be challenging; our samples in the POC year are such that we could only detect impacts at the upper end of the plausible range.
The question is then how to proceed. For the Demonstration year, we plan to use VLFS as the primary outcome (to avoid issues with making multiple comparisons, as described in the section above). For the POC year, however, we propose to use “food insecurity” (i.e., VLSF + LFS) as the primary outcome. Food insecurity is defined as either having LFS (reports of reduced quality, variety, or desirability of diet) or very low food security (reports of multiple indications of disrupted eating patterns and reduced intake) (USDA, 2010). It seems plausible that we will have a greater chance of detecting a statistically significant impact on “food insecurity” than on VLFS alone. It seems plausible that the impact of SEBT for Children will be approximately constant relative to prevalence. That is the case for which we would have a greater likelihood that a detectable impact will occur for the outcome with higher prevalence, even though the MDD will also be higher for that outcome, i.e., “food insecurity”.
After we see results for the POC year, FNS may decide to adopt a joint test for VLFS and “food insecurity” as the primary outcome for the Demonstration year. While that decision needs to be made before the data from the Demonstration year become available, the decision does not have to be made before seeing any data from the POC year. It could be informed by new MDD calculations reflecting the prevalence rates observed in the POC year data, and by measured impacts in that year. For example, VLSF prevalence may be higher than anticipated, making it a strong “stand alone” candidate for primary outcome. Or the estimated impact on “food insecurity” could be surprisingly small, making it important for power reasons to make it the Demonstration year primary outcome.
B.2.3 Degree of Accuracy Needed: Statistical Power and Minimum Detectable Differences
Estimates of MDDs for binary outcomes such as VLFS among children will vary by site and are difficult to predict. Most current prevalence rates are based on the whole year, not the summer. VLFS prevalence rates vary with household income, and although all the study households will have income at or less than 185% of poverty, some sites will have more low-income households than do others. Moreover, VLFS among children prevalence rates vary over time, and some sites will have been hit harder by the recession than others. Finally, most published estimates refer to a 12-month measure of food security, rather than the 30-day measure we will use. Exhibit 2.3 provides a survey of recent estimates of VLFS among children. None of these estimates is exactly applicable, even the national figure for 2008. We believe that the most appropriate estimate is probably the lower right corner—3.2%. It is the right concept—VLFS among children—and it is approximately the right income group (less than 185% FPL), and is relatively recent (2008).
However, this estimate is likely to be too low, for three reasons. First, it is a year-round, not a summer estimate. The premise of the SEBT for Children demonstration is that—in part because the SFSP is smaller than either SBP or NSLP—food security during the summer is worse than during the school year. Second, this estimate is based on 2008 data, and more recent data indicate that the ongoing recession has pushed SNAP caseloads up sharply and may also have an impact on levels of food security. Third, the rates of VLFS among children are likely to vary widely by SFA, reflecting variation in income of certified students (the deeper the poverty, the more likely VLFS) and which SFAs FNS selects. However, we do not know which SFAs will be selected for the 2012 demonstration year, and we do not have estimates of VLFS for the target population at the SFA level.
Exhibit 2.3. Estimates of Very Low Food Security among Children (VLFS-C)
Data Source |
2005 SNDA-III |
2006 CPS |
2007 CPS |
2008 CPS |
Citation |
Run 10/20/10 |
Nord et al. 2007 |
Nord et al. 2008 |
Nord et al. 2009 |
Measure |
18-item, 12-mo child scale |
18-item, 12-mo. child scale |
18-item, 12-mo. child scale |
18-item, 12-mo. child scale |
Households |
|
|
|
|
HH w/ children |
NA |
0.6 |
0.8 |
1.3 |
HH income <100% |
|
2 |
2.4 |
4.1 |
HH income <130% |
|
1.7 |
2.4 |
3.6 |
HH income <185% |
|
1.4 |
2 |
3.1 |
Children |
|
|
|
|
Children—all |
school age |
0.6 |
0.9 |
1.5 |
Child had FRPL in past 30 days |
2.2 |
|
|
|
HH income <100% |
2.8 |
2.1 |
3 |
4.3 |
HH income <130% |
2.8 |
1.8 |
2.8 |
3.8 |
HH income <185% |
2.4 |
1.4 |
2.1 |
3.2 |
Given that we need an estimate of the summer rate of VLFS among children to project MDDs and given that the appropriate rate is unknown, we report MDDs for a range of rates. We believe that 7% is plausible, although rates might range from 3% (the estimate from the CPS 2007) to 15%. Exhibit 2.4 reports MDDs in percentage points and in percent of the baseline rate for this range of VLFS rates. These MDDs are based on our sense of the plausible parameter estimates, and are computed using the following assumptions:
The outcome of interest is VLFS among children.
The design effect (DEFF) is 1.287=1.17x1.10 where 1.10 accounts for the non-response adjustment and 1.17 accounts for the two phase sampling.
An R-squared (explanatory power of model for estimating impacts given spring measurements and other demographic variables not affected by the intervention) of 15%.4 This estimate is an extrapolation from analyses of CPS food security data (two linked years, limiting the sample to households with school age children, and income less than 185% of FPL) conducted for this evaluation.
95% level of confidence and 80% power.
one-tailed test. This is appropriate because we would want to treat an estimate of a negative impact of the program the same as no impact.
The rows in Exhibit 2.4 vary the total sample size (i.e., sum of treatment and control) used in the MDD computations. The first five rows give the MDDs for 1 to 5 sites in the POC year. Given 1,000 survey completes per site (approximately 500 treatment completes and 500 control completes), this corresponds to 1,000 to 5,000 observations. The last 15 rows give the MDDs for 1 to 15 sites in the demonstration year. Given 1,800 survey completes per site (approximately 900 treatment completes and 900 control completes), this corresponds to 1,800 to 27,000 observations.
The crucial questions for interpreting these MDDs are: How large an impact would we expect? How small an impact would be policy relevant? The SEBT for Children is designed to close—at least some substantial part of—the gap in VLFS-C between the school year and the summer. However, we have limited knowledge of the size of the gap. Findings from Nord and Romig (2006) suggest the type of program impacts that are both policy relevant and feasible, based on data about food insecurity and hunger for both the school year and the summer for households with school-age children and incomes less than 185% of FPL.Their analysis found that this measure increases from about 5% to 7%, or roughly by 40%. It is therefore plausible to estimate that summer rates would need to decline by about 30% (approximately from 7% to 5%) to close the summer/school year gap. We use this estimate (of the percentage increase in food insecurity between the school year and the summer) to provide context for whether our MDDs for various analyses are small, moderate, or large.
Relative to this rough estimate of a 30% gap—summer vs. school year, our pooled samples do moderately well in the demonstration year. Focusing on our best guess of prevalence (7%), the MDD in percentage points is 0.8 percentage points, or 12% of the baseline rate. This corresponds to two-fifths of the estimate of the summer/spring gap (40% = 12%/30%).
MDDs are much larger for smaller samples. The pooled POC estimates have an MDD of 28% of the baseline, and thus could only detect a program that eliminated essentially all of the gap. If we assume 9 SNAP sites and 6 WIC sites in the demonstration year, the MDDs are 21% and 15% for the SNAP and WIC sites, respectively (see the row for a sample size of 14,400), or about two-thirds and half of the summer/school year gap, respectively.
There are also subgroup analyses to consider; we must first ascertain whether we can detect impacts in a subgroup (e.g., SNAP participants). We estimate that about half (47%) of children in our sample are also on SNAP. For approximately half the sample, the MDD in percent of baseline is about 1.1%, corresponding to about half of the gap (assuming our earlier gap estimate in both subgroups).
FNS requests other subgroup analyses (as described earlier in SectionB.2.2), including, for example, household characteristics (baseline food security status, household size/number of children, income/SES, urban/rural, food expenditure) and child characteristics (gender, age, grade). Most of these subgroups could reasonably be split into approximately equally sized subgroups. More broadly, for subgroups with one-third of the demonstration sample (i.e., 9,000 observations), the MDD is 21%, or about two-thirds of the gap. This one-third/two-third split is likely to be approximately appropriate for other specified subgroup analyses (e.g., urban/rural, race/ethnicity). Thus, we should be able to detect moderate-sized effects in subgroups as small as one-third of the sample. For subgroups smaller than that, we could only detect very large impacts. Subgroups likely to have prevalences below one-third include baseline participation in other programs (beyond SNAP), disability, and other school characteristics.
Second, note that these are the MDDs for estimates within the subgroups. Of similar or perhaps greater interest are estimates of differential impact across the subgroups. The MDDI (Minimum Detectable Differential Impact) will be about 1.4 times (i.e., square root of two) the MDD for the impact in the subgroup. Thus, for the best case—pooled data and two equally sized subgroups—will be about 1.5 percentage points (1.1 x 1.4). As we expect the program to have impacts in the same direction for both subgroups, the likely difference in impacts is small. Thus, we will have power to detect only the very largest of differential impacts.
Exhibit 2.4. MDDs in Percentage Points and in Percent of the Baseline Rate
MDD in Percentage Points |
|||||||||
|
N Sites |
Control Group Prevalence |
|||||||
N |
POC |
Demo. |
3% |
5% |
7% |
9% |
11% |
13% |
15% |
1,000 |
1 |
|
2.799% |
3.575% |
4.186% |
4.695% |
5.133% |
5.517% |
5.858% |
2,000 |
2 |
|
1.979% |
2.528% |
2.960% |
3.320% |
3.630% |
3.901% |
4.142% |
3,000 |
3 |
|
1.616% |
2.064% |
2.417% |
2.711% |
2.964% |
3.185% |
3.382% |
4,000 |
4 |
|
1.399% |
1.788% |
2.093% |
2.347% |
2.567% |
2.759% |
2.929% |
5,000 |
5 |
|
1.252% |
1.599% |
1.872% |
2.100% |
2.296% |
2.467% |
2.620% |
1,800 |
|
1 |
2.086% |
2.665% |
3.120% |
3.499% |
3.826% |
4.112% |
4.366% |
3,600 |
|
2 |
1.475% |
1.884% |
2.206% |
2.474% |
2.705% |
2.908% |
3.087% |
5,400 |
|
3 |
1.204% |
1.539% |
1.801% |
2.020% |
2.209% |
2.374% |
2.521% |
7,200 |
|
4 |
1.043% |
1.332% |
1.560% |
1.750% |
1.913% |
2.056% |
2.183% |
9,000 |
|
5 |
0.933% |
1.192% |
1.395% |
1.565% |
1.711% |
1.839% |
1.953% |
10,800 |
|
6 |
0.852% |
1.088% |
1.274% |
1.429% |
1.562% |
1.679% |
1.782% |
12,600 |
|
7 |
0.788% |
1.007% |
1.179% |
1.323% |
1.446% |
1.554% |
1.650% |
14,400 |
|
8 |
0.737% |
0.942% |
1.103% |
1.237% |
1.353% |
1.454% |
1.544% |
16,200 |
|
9 |
0.695% |
0.888% |
1.040% |
1.166% |
1.275% |
1.371% |
1.455% |
18,000 |
|
10 |
0.660% |
0.843% |
0.987% |
1.107% |
1.210% |
1.300% |
1.381% |
19,800 |
|
11 |
0.629% |
0.804% |
0.941% |
1.055% |
1.154% |
1.240% |
1.316% |
21,600 |
|
12 |
0.602% |
0.769% |
0.901% |
1.010% |
1.104% |
1.187% |
1.260% |
23,400 |
|
13 |
0.579% |
0.739% |
0.865% |
0.971% |
1.061% |
1.141% |
1.211% |
25,200 |
|
14 |
0.557% |
0.712% |
0.834% |
0.935% |
1.023% |
1.099% |
1.167% |
27,000 |
|
15 |
0.539% |
0.688% |
0.806% |
0.904% |
0.988% |
1.062% |
1.127% |
MDD as Percent of Baseline Prevalence |
|||||||||
|
N Sites |
Control Group Prevalence |
|||||||
N |
POC |
Demo. |
3% |
5% |
7% |
9% |
11% |
13% |
15% |
1,000 |
1 |
|
93.3% |
71.5% |
59.8% |
52.2% |
46.7% |
42.4% |
39.1% |
2,000 |
2 |
|
66.0% |
50.6% |
42.3% |
36.9% |
33.0% |
30.0% |
27.6% |
3,000 |
3 |
|
53.9% |
41.3% |
34.5% |
30.1% |
26.9% |
24.5% |
22.5% |
4,000 |
4 |
|
46.6% |
35.8% |
29.9% |
26.1% |
23.3% |
21.2% |
19.5% |
5,000 |
5 |
|
41.7% |
32.0% |
26.7% |
23.3% |
20.9% |
19.0% |
17.5% |
1,800 |
|
1 |
69.5% |
53.3% |
44.6% |
38.9% |
34.8% |
31.6% |
29.1% |
3,600 |
|
2 |
49.2% |
37.7% |
31.5% |
27.5% |
24.6% |
22.4% |
20.6% |
5,400 |
|
3 |
40.1% |
30.8% |
25.7% |
22.4% |
20.1% |
18.3% |
16.8% |
7,200 |
|
4 |
34.8% |
26.6% |
22.3% |
19.4% |
17.4% |
15.8% |
14.6% |
9,000 |
|
5 |
31.1% |
23.8% |
19.9% |
17.4% |
15.6% |
14.1% |
13.0% |
10,800 |
|
6 |
28.4% |
21.8% |
18.2% |
15.9% |
14.2% |
12.9% |
11.9% |
12,600 |
|
7 |
26.3% |
20.1% |
16.8% |
14.7% |
13.1% |
12.0% |
11.0% |
14,400 |
|
8 |
24.6% |
18.8% |
15.8% |
13.7% |
12.3% |
11.2% |
10.3% |
16,200 |
|
9 |
23.2% |
17.8% |
14.9% |
13.0% |
11.6% |
10.5% |
9.7% |
18,000 |
|
10 |
22.0% |
16.9% |
14.1% |
12.3% |
11.0% |
10.0% |
9.2% |
19,800 |
|
11 |
21.0% |
16.1% |
13.4% |
11.7% |
10.5% |
9.5% |
8.8% |
21,600 |
|
12 |
20.1% |
15.4% |
12.9% |
11.2% |
10.0% |
9.1% |
8.4% |
23,400 |
|
13 |
19.3% |
14.8% |
12.4% |
10.8% |
9.6% |
8.8% |
8.1% |
25,200 |
|
14 |
18.6% |
14.2% |
11.9% |
10.4% |
9.3% |
8.5% |
7.8% |
27,000 |
|
15 |
18.0% |
13.8% |
11.5% |
10.0% |
9.0% |
8.2% |
7.5% |
B.2.4 Unusual Problems Requiring Specialized Sampling Procedures
No specialized sampling procedures are involved in this evaluation.
B.2.5 Use of Periodic Data Collection Cycles to Reduce Burden
This is a one-time study.
B.3 Methods to Maximize Response Rates and Deal with Nonresponse
To maximize response rate in the limited time frame available, we will collect data by telephone and use in-person field locators to follow-up with a subsample of non-responders. Field locators will carry cell phones to allow located household heads to call into the telephone center without the respondent incurring expenses. This design allows us to benefit from the speed of telephone data collection and the high response rates of in-person data collection, while also limiting the likely mode effects if in-person interviewers were instead to complete surveys on laptops. In addition, the survey will be administered in English and Spanish in all sites (and in other languages if required by at least 10% of parents in a site). An added advantage of a telephone survey is that it allows us to interview parents of children who live out of the area during the summer (e.g., with a divorced/separated parent). Summer contact information will be requested on the consent forms.
There will be an aggressive location effort made to increase response to the survey, first with nonresponders sent for advanced location work, followed by field locating with a subsample of non-responders. Two strategies are critical to maximizing response rates: advance letters and extensive field locating procedures.
The use of advance letters (which will be in English on one side and in Spanish on the other) introduces the study and establishes the survey’s legitimacy, which may increase cooperation rates among households. These letters will also be customized within each site using enrollment information about each household head, which should also increase cooperation. The advance letter also represents our initial attempt to locate a household. If the letter is returned without a forwarding address, we will know that the current address for the sample household is invalid, and that, if we cannot find them by phone, that we need to attempt to locate them at a different address. Finally, the letter will include the study’s toll-free telephone number. Respondents will be able to complete an inbound CATI survey with a trained interviewer at our call center if they choose. This may also help increase cooperation rates, because they can call at their convenience.
In an effort to reduce any potential non-response bias, extensive field locating procedures will be implemented to locate sample members. Working with a local site coordinator, the field locators will initiate a ground search, asking neighbors, landlords, property managers, postal carriers, and others where a sample member lives. Interviewers who locate a respondent will use cell phones to call into our telephone center from the respondent’s household. Calls from field interviewers will go to the same CATI call center used for phone interviews. Once the connection to the telephone interviewer is made, the field staff will then hand the cell phone to the respondent, who will then complete their interview with the telephone interviewer. Respondents reached by telephone will receive a $10 incentive (a gift card) immediately after the completion of the interview from the field interviewer.
B.4 Tests of Procedures or Methods to be Undertaken
The procedures and instruments to be used in the Evaluation of the SEBTC Benefits Demonstration are similar to those that have been developed, tested, and administered for other studies of child nutrition programs and WIC conducted by Abt Associates and its subcontractor, Mathematica. In January, 2011, the household instrument was pre-tested with nine respondents. During the pre-test of the household interview, interviewers made note of questions that needed clarification, questions that required adjustments, and those that needed to be reworded. The time required for each interview was also recorded. The test included a short session asking the respondents their opinions of the survey/interview, including what should be changed and what would make it better. The results of the pilot test were used to revise the instruments.
Field procedures will be reviewed with proof-of-concept grantees in conference calls conducted in winter 2010-2011. Revised field procedures will incorporate any information gleaned from these initial calls. In addition, field procedures will be tested and thoroughly vetted during the POC year.
B.5 Individuals Consulted on Statistical Aspects and Individuals Collecting and/or Analyzing Data
The design for the study was developed by the contractor, Abt Associates Inc., under the direction of: Ann Collins, Project Director; Michael Battaglia, Sampling Statistician; and Jacob Klerman, Director of Analysis. Ms. Collins may be reached at (617) 349-2664 or [email protected]; Mr. Battaglia may be reached at (617) 349-2425 or [email protected]; Mr. Klerman may be reached at (617) 520-2613 or [email protected]. The design was also reviewed by Dr. Stephen Bell, who can be reached at 202-635-1721 or [email protected] and by reviewers from Mathematica, Ronette Briefel (at 202-484-922 or [email protected]) and Anne Gordon (at (609) 275-2318 or [email protected]). In addition, Mathematica Policy Research consulted with Fran Thompson, National Cancer Institute, NIH (phone 301-435-4410).
In addition, Dr. Hoke Wilson and Dr. Ted Macaluso of FNS’ Office of Research and Analysis have reviewed the study design and instruments. Dr. Wilson can be reached at (703) 305-2131 or [email protected]. Dr. Macaluso can be reached at (703) 305-2121 or [email protected]. Abt Associates Inc. and its subcontractor, Mathematica, are responsible for all data collection and analysis for this study.
Bloom HS, Hill CJ, Riccio JA. 2003. Linking program implementation and effectiveness: Lessons from a pooled sample of welfare-to-work experiments. Journal of Policy Analysis and Management 22(4):551-575.
Nord, M, Romig K. 2006. Hunger in the summer: Seasonal food insecurity and the National School Lunch and Summer Food Service Programs. Journal of Children and Poverty 12(2): 141-158.
Raudenbush SW, Bryk, AS. 2002. Hierarchical linear models (2nd ed.). Newbury Park, CA: Sage Publications.
Schochet PZ. 2008. Guidelines for testing in impact evaluations of educational interventions. Princeton, NJ: Mathematica Policy Research.
Schochet PZ. 2009. An approach for addressing the multiple testing problem in social policy impact evaluations. Evaluation Review 33(6):537-567.
USDA, Economic Research Service (2010). Food Security in the United States: Definition of Hunger and Food Security. http://www.ers.usda.gov/Briefing/FoodSecurity/labels.htm#labels
1 Even if we had income information, it is not clear that we could use it. Our current estimates imply that some of the sites are only barely big enough to support the target number of cases—even when using every eligible child, regardless of income. This is especially true in sites that will use active consent. As we discuss below, we project moderate failure to provide active consent. Such non-consent combined with survey non-response implies that we may have trouble achieving the project sample sizes. There simply are not enough children. Given that problem, oversampling is not feasible. There simply are not enough very poor children in the sites.
2 See http://www.census.gov/acs/www/Downloads/survey_methodology/acs_design_methodology_ch04.pdf
3 It is also possible that the longitudinal aspect of the data will induce changes in impact; i.e., that the impact of someone in the treatment group (or control group) in two consecutive years will be different from the impact of being in the treatment group (or control group) in only one year. It seems unlikely that such differential impacts will be large. In principle, we could test for differences, but our sample sizes are such that we could only detect implausible large differential impacts (several percentage points).
4 To get a rough sense of predictive ability, we linked the 2008 and 2009 CPS Food Security modules and used the 2008 variables (including 2008 VLFS-C) to predict the 2009 outcome, for the sample of households with school age children and income below 185% of FPL. Exact results vary with specification, but not above 7%. Our models should have slightly better predictive ability. The gap between the two interviews should be smaller and we will ask a broader range of questions—some specifically to raise the predictive ability of the model (e.g., detailed income and food pantry use). Nevertheless, this analysis suggests that predicting VLFS-C, a rare event, is difficult and the R2 will be small.
Abt
Associates Inc. & Mathematica Policy Research, Inc.
| File Type | application/msword |
| File Title | Abt Single-Sided Body Template |
| Author | NicholsonJ |
| Last Modified By | hwilson |
| File Modified | 2011-03-16 |
| File Created | 2011-03-16 |
© 2026 OMB.report | Privacy Policy