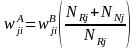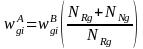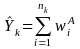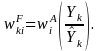Worker Classification Survey-OMB Attachment D-Estimation
Worker Classification Survey-OMB Attachment D Estimation 09-13-13.docx
Worker Classification Survey
Worker Classification Survey-OMB Attachment D-Estimation
OMB: 1235-0028
Attachment D: Weighting and Estimation Procedures
Worker Classification Survey: Weighting Protocol
The Worker Classification Survey features a national dual-frame landline and cellular random digit dial (RDD) probability sample design. The landline and cell phone sampling frames overlap, as some employees age 18 years and older have both a residential landline in their household and a cell phone (dual users). While many dual frame RDD surveys treat the cell phone as a personal device, this survey will treat the cell phone as a household device. Interviews will conduct a household roster to identify all eligible workers in both the landline and cell phone samples. The weighting procedures described here account for the overall probability of selection, sampling frame integration, and appropriate non-response and post-stratification ratio adjustments.
The reciprocal of the probability of selection is referred to as the “base weight.” The base weight is the product of several components. The first component is the inverse of the selection probability of the telephone number. The second component is an adjustment for the number of voice-use landline numbers in the household (equal to 0 for cell-only households) and the number of non-business adult-use cell phones in the household (equal to 0 for landline-only households). The third component of the base weight accounts for the fact that in households with multiple eligible adults, only one eligible adult is randomly selected for the extended interview. This adjustment weights up those respondents proportional to the total number of eligible adults in the household. We may decide to put caps on the maximum values allowed for these adjustments to avoid extreme base weight values.
Due to the overlap in the landline and cellular RDD frames, a frame integration weight (or “compositing factor”) is needed to combine the two sample components. Three major approaches to choosing this compositing factor are encountered in the existing theory and practice of the dual frame surveys.1 The first one is to compute the integration weight based on the ratio of the effective sample sizes of the landline and cell phone samples. Specifically, the frame integration weight for dual user (landline and cell) respondents in the landline sample will be the ratio of the effective number of dual service landline cases to the total effective number of dual service cases in both samples. Similarly, the frame integration weight for the dual service cell sample cases will be the ratio of the effective number of dual service cell sample cases to the total effective number of dual service cases in both samples. This general compositing approach assumes that the dual service households from each of the two samples are random samples from the population of dual service households. Given the differential nonresponse that occurs, however, this assumption does not hold in practice.2 To address this issue, the survey will include a question for dual service households measuring whether most incoming calls are received on a cell phone (“cell mostly”) or on a landline phone (“landline mostly”). Using this question, the second possible compositing factor proposed in Brick, Cervantes, Lee and Norman (2011)3 aims to reduce non-response bias. This compositing factor is a function of the response rates of the dual users in the landline and cell components (see equation 4 in Brick et. al 2011). The third widely used compositing factor is aimed at minimizing the design effect (i.e., the variance of the resulting estimates), and depends on the observed variances of the variables of interest in the landline and cell subsamples of the dual users. This is often a compromise factor, as different response variables tend to have different design effects.
While the non-response reducing compositing factor appears to be the most promising, it is associated with increase in variances. We shall compare and contrast the three approaches, and quantify the potential biases and efficiency gains due to different compositing factors. The best performing compositing approach (in terms of reducing estimated mean square error) will be used in the weighting. Landline-only and cell-phone-only cases will be assigned a frame integration weight of 1. The product of the base weights and the frame integration weights are referred to as “design weights” and will be used as the input weight for the non-response adjustment.
The
screener non-response adjustment will need to be calculated at the
household level for telephone numbers for which no screening
interview is conducted. The adjustment cells will be based on Census
Region for both the cell and landline samples. The screener
non-response-adjusted weight,
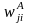 ,
for the i-th household in region j will be computed as
,
for the i-th household in region j will be computed as
|
(1) |
where
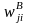 is the design weight, NRj
is the weighted sum of screened households in region j,
and NNj
is the weighted sum of unscreened households in region j.
is the design weight, NRj
is the weighted sum of screened households in region j,
and NNj
is the weighted sum of unscreened households in region j.
The extended interview non-response adjustment will account for cases in which an eligible adult was selected for the extended interview, but the extended interview was not completed. The extended interview non-response adjustment, which is at the person level, will be done within specified non-response adjustment weighting classes of persons, and these factors will be applied to the design weights adjusted for household non-response, to compensate for unit non-response. The weighting classes will be defined by the number of eligible adult workers in the household. Demographics such as age and gender are not being collected on the screener and, therefore, will not be available for use in the extended interview non-response adjustment.
The
non-response-adjusted weight,
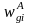 ,
for the i-th responding eligible person in weighting class g
will be computed as
,
for the i-th responding eligible person in weighting class g
will be computed as
|
(1) |
where
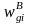 is the weight that includes the design weight and the
household screener non-response adjustment, NRg
is the weighted sum of eligible responding persons in
weighting class g, and NNg
is the weighted sum of non-responding persons in weighting
class g.
is the weight that includes the design weight and the
household screener non-response adjustment, NRg
is the weighted sum of eligible responding persons in
weighting class g, and NNg
is the weighted sum of non-responding persons in weighting
class g.
To help reduce possible residual non-response and non-coverage errors, the final estimation weights will also include a post-stratification adjustment to reflect the most recent population information available. The target population for the Worker Classification Survey is adults (age 18 and older) residing in the U.S. who did work for pay during the previous 30 days. We will compute control totals for this population from the most up-to-date publically available March Current Population Survey, Annual Social and Economic Supplement (CPS-ASEC) micro datafile. Specifically, we will use the CPS to estimate the total size of the target population, along with demographics distributions for gender, age, education, race, Hispanic ethnicity, and region. These estimates will be computed for adults in the CPS who worked last week. In addition, we will use the most up-to-date publically available National Health Interview Survey Pubic Use File (PUF), to compute the distribution for telephone service groups based on employed adults.
The post-strata will be constructed using the relevant demographic variables in the survey dataset. The proposed initial post-strata are as follows and collapsing rules are detailed below:
GENDER (1=Male, 2=Female)
AGE (1=18 to 29, 2=30 to 39, 3=40 to 49, 4=50 to 59, 5=60 and above)
EDUCATION (1=High school graduate/GED or less, 2=Some college or Associate degree, 3=Bachelor’s degree, 4=Master’s, Doctorate, or professional school degree (e.g., MD, DDS, JD))
RACE_ETHNICITY (1=White only non-Hispanic, 2=Black only non-Hispanic, 3=Asian only non-4=Hispanic, 5=Other race or mixed race non-Hispanic, 6=Hispanic)
REGION (1=Northeast, 2=Midwest, 3=South, 4=West)
PHONESERVICE (1=Cell phone only, 2=Landline only, 3=Dual service)
We will fill missing data on these weighting variables using chained equations imputation methodology.4 This methodology, also known as the fully conditional specification, proceeds by fitting appropriate regression models (linear for continuous response, logistic for binary response, ordinal logistic for the Likert scales, etc.) and drawing from the conditional distributions to impute the missing data. The process is repeated several times to ensure internal consistency of the imputed values with one another.
The general approach for making the post-stratification adjustment will be as follows. Let Yk denote the aggregate number of persons in post-stratum k from the population controls and let
|
(2) |
denote
the corresponding estimate from the sample, where
 is the interview non-response-adjusted weight defined
previously and nk
is the number of responding persons in post-stratum k.
The final weight for person i in post-stratum k will
then be computed as
is the interview non-response-adjusted weight defined
previously and nk
is the number of responding persons in post-stratum k.
The final weight for person i in post-stratum k will
then be computed as
|
(3) |
The above adjustment has the effect of forcing the weighted estimate of the aggregate number of employees in a post-stratum to agree with the corresponding independent population control. Given that the sample will be post-stratified to several variables, we plan to use raking ratio estimation to calculate the final weights. The distribution of the weights will be examined for any extreme values. If extreme values are present, then the weight distribution will be trimmed in order to avoid undue variation in the weights (i.e., a large design effect) as well as undue influence on survey estimates from a small number of cases.
As mentioned in Part B, the reference period used to define the eligible population for the Worker Classification Survey is “employed for pay in the last 30 days.” This is different from the “last week” period used in the CPS. In addition to the weighting described above, we plan to compute an identical weight (and replicate weights) based only on Worker Classification Survey respondents who report having been employed “last week” based on a question asked in the extended interview. This way, we can compare weighted survey estimates based on the full sample to weighted survey estimates based on the sub-sample of respondents who match a universe that can be defined precisely in the CPS. We expect to observe minimal differences between these two sets of estimates. If, however, meaningful differences are observed (e.g., an average of more than 1.5 percentage points for a set of key survey estimates), then consideration will be given to using the experimental weights as the final survey weights and dropping the respondents who did not work last week from the dataset. This is based on the logic that the experimental weights may be more accurate because the survey target population and the population identifiable in the CPS would be the same.
To appropriately account for the complex survey design features and weight adjustments when computing the standard errors, we propose to use the complex survey bootstrap method.5,6 In the bootstrap methods, samples with replacement are taken within the sampling strata (defined as the sample frames), and replicate weights are produced that account for the multiplicity of the selection of the sampled units. Unlike some other replication methods, bootstrap weights vary for each observation and each replication, thus making it more difficult to identify the sampling units whose weights vary together, and hence better protecting confidentiality of the survey respondents.
1 Lohr, S. (2009). Multiple-Frame Surveys. Ch. 4 in D. Pfeffermann and C. R. Rao, editors, Handbook of Statistics, Vol. 29A: Sample Surveys: Design, Methods and Applications, Elsevier/North Holland.
2 Kennedy, C. (2007). “Evaluating the Effects of Screening for Telephone Service in Dual Frame RDD Surveys.” Public Opinion Quarterly, Vol 71, pp. 750-–771.
3 Brick, J.M., I.F. Cervantes, S. Lee and G. Norman (2011). Nonsampling errors in dual frame telephone surveys. Survey Methodology, vol. 37, no. 1, pp. 1–12.
4 White, I. R., P. Royston and A. M. Wood (2011). Multiple imputation using chained equations: Issues and guidance for practice. Statistics in Medicine, vol. 30, no. 4, pp. 377–399.
5 Rao, J. N. K, C. F. J. Wu, and K. Yue (1992). Some recent work on resampling methods for complex surveys. Survey Methodology, vol. 18, no. 2, pp. 209–217.
6 Kolenikov, S. (2010). Resampling variance estimation for complex survey data. The Stata Journal, vol. 10, no. 2, pp. 165–199.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Jan Nicholson |
| File Modified | 0000-00-00 |
| File Created | 2021-01-29 |
© 2025 OMB.report | Privacy Policy