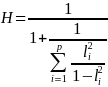Attachment C-Analytical Approaches
IMPAQ_Part_A&B_AJC_Accessibility_Study_Attachment_C_020414.docx
Evaluating the Accessibility of American Job Centers for People with Disabilities
Attachment C-Analytical Approaches
OMB: 1290-0010
ATTACHMENT C.
ANALYTIC APPROACHES
1. Reliability in Item Response Theory (IRT) Model
Classical
test theory-based reliability indices such as Cronbach’s Alpha
are not appropriate when 1) the length of the test may differ for
each respondent, and 2) the test used Item Response Theory (IRT)
methods, where the measurement error is a function of the latent
construct level (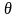 ).
The reliability coefficient for the AJC measure is, therefore,
calculated as the marginal
reliability
(Sireci, Thissen, & Wainer, 1999), which is equivalent to
internal consistency estimates of reliability.
).
The reliability coefficient for the AJC measure is, therefore,
calculated as the marginal
reliability
(Sireci, Thissen, & Wainer, 1999), which is equivalent to
internal consistency estimates of reliability.
First
we determine the marginal measurement error variance,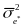 ,
across all respondents,
,
across all respondents,
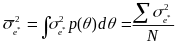 ,
,
where
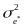 is the square of the standard error of the latent construct estimate,
is the square of the standard error of the latent construct estimate,
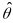 .
Thus, the marginal measurement error variance can be estimated as the
average of the squared standard error of
.
Thus, the marginal measurement error variance can be estimated as the
average of the squared standard error of
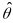 .
Then, we estimate the marginal reliability as:
.
Then, we estimate the marginal reliability as:
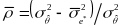
where
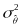 is the variance of the observed
is the variance of the observed
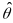 estimates.
estimates.
Coefficient H
The coefficient H1 is the measure of stability of a construct as reflected in the data on the chosen indicators, which is the squared correlation between the latent construct and the optimum linear composite from the survey items. The coefficient H indicates the maximum reliability of construct measured by a set of survey items. The coefficient H is defined as:
2. Non Response Weighting: Mean and Variance
For the derivation of the non-response weighted mean and variance, the IMPAQ team will utilize the following equations (Little &Vartivarian, 2005).
The
weight mean,
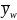 ,
is defined as:
,
is defined as:
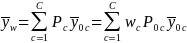
where
C indicates respondents and non-respondents,
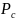 is the proportions of sampled cases for group c,
is the proportions of sampled cases for group c,
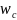 is the nonresponse weights, and
is the nonresponse weights, and
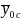 is the respondent mean for group c. Then the mean of Y (outcome) for
respondents,
is the respondent mean for group c. Then the mean of Y (outcome) for
respondents,
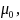 and non-respondents,
and non-respondents,
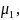 becomes:
becomes:
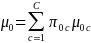
and
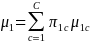
where
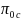 is the probability of being in the respondent group and
is the probability of being in the respondent group and
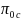 is the probability of being in the non-respondent group.
is the probability of being in the non-respondent group.
The
variance of weighted mean, V(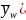 ,
is defined as:
,
is defined as:
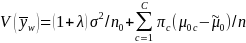
where
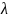 is the variance of the nonresponse weights,
is the variance of the nonresponse weights,
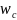 ,
and
,
and
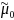 is the respondent mean adjusted for the covariates.
is the respondent mean adjusted for the covariates.
3. Partial Credit Model
The partial credit model (PCM; Masters, 1982; Wright & Maters, 1982) is a polytomous extension of the Rasch model (Rasch, 1960) or 1-parameter logistic model (Birnbaum, 1968). The AJC survey includes both dichotomously scored questions. For example, for dichotomously-scored questions 0 will be assigned for No and 1 for Yes. For polytomously-scored questions 1 will be assigned for rarely or not at all, 2 for some of the time, 3 for most of the time and 4 for always. The PCM is an appropriate model to estimate the continuous latent construct estimates (i.e. accessibility level) from ordered categorical responses (i.e. both dichotomously and polytomously scored questions. This model assumes that only item response defines the individual proficiency and all item responses are independent conditional on the individual proficiency. The PCM model is typically defined as:
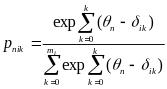 (1)
(1)
where
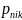 is the probability of person n scoring k on item i,
is the probability of person n scoring k on item i,
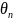 is
the estimate of the latent construct level, and
is
the estimate of the latent construct level, and
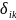 refers to the step value (i.e. item difficulties). The better way to
interpret the formula is to convert it into log-odds or logit form.
The logit form of PCM equation is,
refers to the step value (i.e. item difficulties). The better way to
interpret the formula is to convert it into log-odds or logit form.
The logit form of PCM equation is,

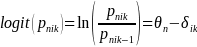 (2)
(2)
where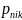 is the probability of response for person n to the item i in category
k,
is the probability of response for person n to the item i in category
k,
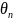 is
a latent ability or proficiency of person/job center n, and
is
a latent ability or proficiency of person/job center n, and
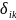 is item estimates on category k in item i.
is item estimates on category k in item i.
PCM
estimates the expected response probability of each response
categories given
the latent construct score (see Exhibit C1), characterizing the
properties of item. The height of each line is a probability of
endorsing each category
given the latent construct level.
The difficulty
or step parameter,
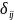 ,
is where two successive curve intersects.
,
is where two successive curve intersects.
Exhibit
C1: Category Response Curve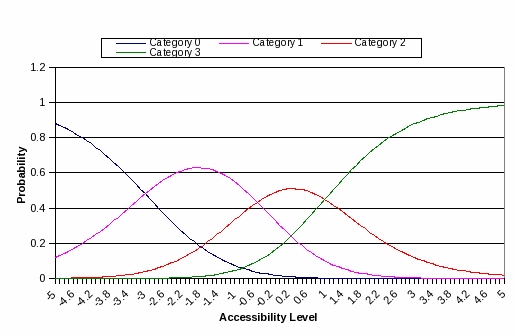
4. Facet Model
The IMPAQ team will use the extension of the Partial Credit Model because AJC scale development requires evaluating and accounting for the impact of external factors, such as SDR and SNR. As statistical remedies for SDR and SNR effects, the IMPAQ team will use the Facet model (Linacre, 1989; Eckes, 2011) which allows for the examination of the effect of external factors such as respondent types and survey non-respondents. The Facet model provides an avenue to explore and correct for bias in survey responses. The Facet model estimates the magnitude of the responder’s bias (i.e., responder as a facet) within the IRT framework (see Equations 3-6). The Facet model (equations 4-6) and PCM model (equation 3) provides the same accessibility estimates when there is no ‘facet’ in the model (e.g. SDR and SNR) or if facet effects (e.g. SDR effect) is zero.
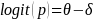 (3)
(3)
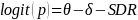 (4)
(4)
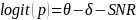 (5)
(5)
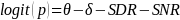 (6)
(6)
Facet
models will provide the parameter estimates for all SDR and SNR
levels and the resulting accessibility construct estimates,
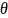 ,
which will be adjusted for SDR and/or SNR effects. The magnitude of
SDR and SNR parameters will indicate the severity of the SDR and SNR
effect.
,
which will be adjusted for SDR and/or SNR effects. The magnitude of
SDR and SNR parameters will indicate the severity of the SDR and SNR
effect.
Other IRT models for polytomous responses such as Rating Scale Model (RSM) or Generalized Partial Credit model (GPCM) are also considered. We have determined neither RSM nor GPCM meets our objectives because: 1) RSM was not appropriate due to the presence of mixed response categories (e.g. binary questions and sliding scale questions) in surveys and 2) inability for GPCM to accommodate other facets such as SDR and SNR effects.
5. Item Parameter Estimation with Missing Responses
IRT models including PCM and Facet modes provides the estimates of a unique set of item parameters measuring a different range of latent constructs of interest. Estimation of item parameters involves maximizing a likelihood function:
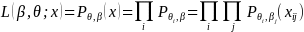 (7)
(7)
with respect to the parameters β and θ, where β is a vector of step and facet parameters and θ is a vector of latent construct scores. A likelihood function is computed for each respondent given a response vector. The equation 7 implies that the estimation of item parameters utilizes all information available (i.e. missing responses are excluded from the construction of the likelihood function), allowing to respond to different set of survey questions.
This property allows the implementation of the matrix survey deployment plan. Responses from web surveys and site visits will be combined into one dataset with the indicator clearly identify the mode of data collection. This dataset will be estimated jointly providing all parameters on the same scale (i.e. item parameters, latent construct estimates and facet parameters), which eliminates the use of post-hoc adjustment or triangulation of survey scale.
Equation 8 is maximized by the Marginal Maximum Likelihood (MML) estimation (Bock and Aiken, 1981), which produces the consistent estimates of item parameters via the EM-algorithm. The MML integrates out the latent construct parameter, θ, to obtain the marginal distribution of the response pattern X:
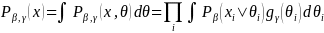 (8)
(8)
,
where
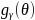 is a probability density function of the θ distribution which
is distributed normally with
is a probability density function of the θ distribution which
is distributed normally with
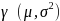 .
. Both β
and
.
. Both β
and
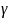 parameters are simultaneously estimated in MML by maximizing the
marginal probability of the observed response pattern
parameters are simultaneously estimated in MML by maximizing the
marginal probability of the observed response pattern
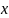 with respect to the
parameters β
and
with respect to the
parameters β
and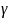 :
:
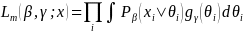 (9)
(9)
6. Estimation of Latent Score
Suppose
that a AJC staff is presented N
survey questions, indexed
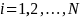 ,
and the AJC staff’s response categories on these survey
questions are given in the score vector
,
and the AJC staff’s response categories on these survey
questions are given in the score vector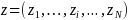 .
Let each survey question be characterized by a vector of item
parameters
.
Let each survey question be characterized by a vector of item
parameters
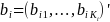 ,
where
,
where
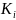 is the maximum category for survey question
is the maximum category for survey question
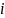 ,
and collect all item parameters in the vector
,
and collect all item parameters in the vector
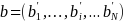 .
Then the response likelihood function of PCM model is computed as:
.
Then the response likelihood function of PCM model is computed as:
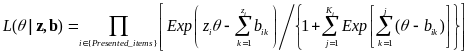 .
.
The method calculates the IRT construct score, θ, which maximizes the likelihood function for the web survey’s observed response vector. The Newton-Raphson method is used to determine the theta value from the likelihood function.
Each unique response pattern and set of presented items gives rise to a distinct shape of likelihood function. Thus, the scoring method takes into account both the number of item score points the respondent endorsed as well as the difficulty of the items the AJC staff was given. This property allows having different versions of surveys, including unique responses from site visits as well as computing subscale scores such as accessibility subscale scores for a different type of disabilities. We will examine if the subscale scores can characterize the accessibility level of AJC for various types of disabilities.
7. Estimation of Error
The
standard error estimates (i.e. standard error of parameters, SE) in
IRT is a function of set of item responses endorsed by respondents2,
which is a square root of an inverse of sum of information provided
by all responded items expressed in the equation below. In IRT, each
item provides the information
about the respondent’s construct level or ability, represented
by the item information,
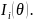 The standard error of estimate,
The standard error of estimate,
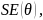 is the square root of the inverse of sum of information across all
responded items:
is the square root of the inverse of sum of information across all
responded items:
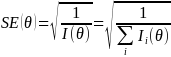
Where
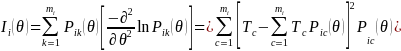
where
T
is a vector of survey responses unique to each respondent such as
T=(1,
3, 4, 3, 2, ….,3) and the response probability of survey
question i endorsing
category k
given the latent score of θ,
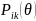 ,
comes from equation C1 on Appendix C. A benefit of the IRT model is
that it generates the standard errors of estimates (i.e. precision of
estimates) based on the pattern of endorsed survey question
responses2.
,
comes from equation C1 on Appendix C. A benefit of the IRT model is
that it generates the standard errors of estimates (i.e. precision of
estimates) based on the pattern of endorsed survey question
responses2.
8. IRT Fit Indices
Fit-statistics are valuable indices for examining item and person responses. Fit statistics provide information about how well items and respondents fit the IRT model. The un-weighted fit may be referred as Outfit mean-square and weighted fit as Infit mean-square that was originally proposed by Wight and Masters (1982).
These statistics indicated the discrepancy between observed item responses and the predicted item responses based on the IRT model for each item. Both fit statistics had an expected value of 1. Values substantially greater than 1 indicated unmodeled variation (model underfit), and values less than 1 indicated a lack of stochasticity (model overfit) (Wright & Masters, 1982).
Infit values are generally related to item construction that is sensitive to consistency of item responses. Outfit values when high indicate unexpected responses, such as careless mistakes on the easiest items by students of known higher ability or guessing on hard items by students of known lower ability (Meijer & Sijtsma, 2001). The IRT analysis also provides fit statistics to the latent construct parameters, which potentially identifies erratic respondents (e.g. random responses) or highly deterministic response patterns (e.g. potential sign of systematic biases such as SDR). Adequate range of fit indices for survey is suggested between 0.6 to 1.4 (Bond & Fox, 2001; Smith, Schumacker, & Bush, 1998). WINSTEPS (Linacre, 2013) manual also provides a guideline for fit evaluation.
1 Hancock, G. R., & Mueller, R. O. (2001). Rethinking construct reliability within latent variable systems. In R. Cudeck, S. du Toit, & D. Sörbom (Eds.), Structural Equation Modeling: Present and Future — A Festschrift in honor of Karl Jöreskog. Lincolnwood, IL: Scientific Software International, Inc.
2 Embretson, S.E. (1996). The new rules of measurement. Psychological Assessment, Vol 8(3), 341-349.
OMB Parts A &
B Attachment C – Page
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Futoshi Yumoto |
| File Modified | 0000-00-00 |
| File Created | 2021-01-27 |
© 2026 OMB.report | Privacy Policy