EDECH OMB Part B AG-3198-C-14-0019 rev 2015 08 17
EDECH OMB Part B AG-3198-C-14-0019 rev 2015 08 17.docx
Evaluation of Demonstration Projects To End Childhood Hunger
OMB: 0584-0603

Evaluation of Demonstration Projects to End Childhood Hunger (EDECH)
Contract Number: AG-3198-C-14-0019
OMB Supporting Statement
Part B: Collections of Information Employing Statistical Methods
Project
Officer: Danielle Berman
Office of Policy Support
U.S.
Department of Agriculture
Food and Nutrition Service
3101 Park Center Drive
Alexandria, VA 22302
CONTENTS
PART B: COLLECTIONS OF INFORMATION EMPLOYING STATISTICAL METHODS
B1. Description of respondent universe and sampling methods 3
B.1.1. Sample Frame Determination 5
B.1.2. Design Features 5
B.1.3. Response Rates and Nonresponse Bias Analysis 7
B2. Procedures for the collection of information 8
B.2.1. Estimation Procedures 8
B.2.2. Statistical Power 14
B3. Methods to maximize response rates and deal with nonresponse 27
B4. Description of tests of procedures 30
B5. Individuals consulted on statistical aspects of the design 30
References 31
B.1. Description of respondent universe and sampling methods
Describe (including a numerical estimate) the potential respondent universe and any sampling or other respondent selection method to be used. Data on the number of entities (e.g., establishments, State and local government units, households, or persons) in the universe covered by the collection and in the corresponding sample are to be provided in tabular form for the universe as a whole and for each of the strata in the proposed sample. Indicate expected response rates for the collection as a whole. If the collection had been conducted previously, include the actual response rate achieved during the last collection.
The Evaluation of Demonstration Projects to End Childhood Hunger (EDECH) will assess the effectiveness of demonstration projects proposed by five awardees: Chickasaw Nation, Kentucky, Navajo Nation, Nevada, and Virginia. Separate study designs have been developed and are being implemented for each demonstration, based on awardees’ intervention plans and the feasibility of randomizing households, schools, school districts, or communities to treatment or control/comparison groups. Nevada will conduct household-level random assignment (RA) with two treatment arms, Kentucky will conduct household-level RA with a single treatment arm, and the other three projects will conduct cluster-level random assignment, where the clusters are either geographic regions (Tribal chapters), schools, or school districts. The reason that household-level RA will be used for two grantees and cluster-level RA used for the other three districts is related to the nature of the intervention in each site. In Nevada and Kentucky, benefits (for example, enhanced SNAP benefits) are delivered to individual households, and so household-level RA is possible. In the other three sites, the intervention—at least in part—is provided to groups of households rather than individual households. The intervention in Navajo Nation involves the assignment of a Food Assistance Navigator (FAN) to a tribal chapter to help residents of the chapter more easily access public food assistance resources. In Virginia, the intervention is provided at the school level (i.e., universal provision of three meals a day in treatment schools). Exhibit B.1a summarizes key features of each of the designs planned for the evaluation.
Exhibit B.1a. Evaluation designs for demonstration projects
Evaluation approach (project(s)) |
Implementation |
Design features |
Household-level RA with multiple treatments (Nevada) |
|
|
Household-level RA with single treatment (Kentucky) |
|
|
Clustered RA (Chickasaw Nation, Navajo Nation, and Virginia) |
|
|
This section describes the sampling procedures that will be used for the demonstrations, including: (1) sample frame determination, (2) design features specific to the household-level and cluster-level random assignment designs, and (3) expected response rates and nonresponse analysis.
B.1.1. Sample Frame Determination
The demonstration projects’ designs will dictate how the evaluation contractor identifies the study sample. For each of the designs of the five projects, the first step will be to obtain a list of the full population eligible for the intervention being evaluated to serve as the sampling frame. The frame will be defined so that it is consistent with the project’s target population, and will depend on project design and goals. All projects aim to reduce childhood hunger and food insecurity, and the frames will include only households (or families) with children. The frames focus on participants in SNAP in Kentucky and Nevada. Sampling frame information will come from State or local offices, school districts, or community health organizations depending on the project design (see Exhibit B.1.1). Study samples will be randomly selected from eligible households with children; the unit of analysis is households in all projects.
Exhibit B.1.1. Sample frame and evaluation subsample for EDECH
Grantee |
Number of eligible households in the sample frame |
Number of households selected for the evaluation subsample |
Chickasaw Nation |
8,812 |
4,750a |
Kentucky |
14,151 |
4,504b |
Navajo Nation |
13,294 |
5,750a |
Nevada |
11,734 |
6,746b |
Virginia |
6,418 |
4,750a |
a Represent the number of eligible and consented households.
b Kentucky and Nevada households will be randomly assigned to the treatment or control group following completion of the baseline survey. The sample sizes reflect the starting sample and assume rates of 85 percent eligibility, 80 percent consent, and 80 percent response, and account for households that could be eligible at the time of the baseline interview but exit SNAP pre-implementation and therefore become ineligible post-interview.
B.1.2. Design Features
Two awardees (Nevada and Kentucky) will use RA at the household level for the study design. At heart, RA is as simple as the flip of a coin, with a household assigned to a treatment or control group on the basis of a random process. A more complex RA process may be necessary to meet demonstration objectives; the contractor will balance analytic concerns with the projects’ practical and policy-related needs. For example, the contractor could use an explicit stratified RA to help address a goal of serving a particular mix of households. In Kentucky, the contractor will stratify the selection of households by county of the SNAP household and the presence/absence of earnings, such that in each stratum the probability that a given household will be selected into the household sample is the same. The RA process can also accommodate special cases to help address practical concerns, such as to avoid situations in which SNAP households in the same residence are assigned to different benefit levels. In this case, families in the same residence would be treated as a single unit during RA so that both households are assigned to either the treatment or the control group.
In the clustered RA design the contractor will conduct random assignment at the cluster level defined by a school district, school, or Tribal chapter. As discussed above, before random assignment the contractor will consider a pairwise matching design, in which pairs of clusters with similar characteristics are formed and, within each pair, one cluster is assigned to the treatment group and the other to the control group. This design makes it less likely that households in the two groups would differ from one another by chance, thus improving the design’s statistical power (Imai et al. 2009).
B.1.3. Response Rates and Nonresponse Bias Analysis
As discussed, a primary objective of this study is to be able to determine the impact of each of the individual projects to require a sufficient level of statistical precision (plus or minus 5 percentage points for the impact estimates). As noted above and in Part A, in three of the five intervention sites, the MDIs are constrained by the number of project clusters (school districts, schools, and Tribal chapters) and the number of students in the recruited project school districts, schools, and Tribal chapters. Therefore, this study must achieve the highest response rate possible among the available sample in the three sites with cluster designs to reach the desired quality for the project assessments. The target response rate for the baseline and follow-up household surveys is 80 percent or more (Attachment H.1). Because all demonstration projects will serve high-need, hard-to-reach populations, meeting this target will be challenging. To achieve this the contractor will utilize an incentive program coupled with an extensive follow-up strategy for nonrespondents to maximize the study precision; these are described in section B3. If any of the surveys do not achieve an 80 percent response rate, the contractor will conduct a nonresponse bias analysis to rigorously assess relationships between household characteristics and nonresponse. To provide a range for the actual MDDs that may be obtained from this study the burden table and the MDD tables using two scenarios, 80 percent response rate and a 60 percent response rate, are presented, The level of burden would be less at a 60 percent response rate, but the sample will fail to meet the target precision requirements and as such will be less effective at measuring the impact of the program interventions (An alternate table estimating burden assuming a lower household survey response rate, 60 percent, is included as Attachment H.2.)
To assess whether nonresponse bias exists, the contractor will obtain as much information as possible on the full study sample from the sample frame, including demographic characteristics, income, and household structure/composition. If possible, the contractor will obtain data on project participation and experiences during the baseline and follow-up periods from administrative data. The follow-up data will be particularly valuable in the nonresponse analysis. Although nonresponse analysis typically compares respondents and nonrespondents on the basis of characteristics and experiences at baseline, these groups will be compared on the basis of actions during the follow-up period, which may be closely correlated with the outcomes of interest. The contractor will also (1) compare respondents and nonrespondents within the treatment and comparison groups, (2) test the significance of differences between respondents’ and nonrespondents’ characteristics, (3) look at whether these differences are the same in the treatment and comparison groups, and (4) compare characteristics of the respondent and nonrespondent samples with those of the frame.
B.2. Procedures for the collection of information
Describe the procedures for the collection of information including:
Statistical methodology for stratification and sample selection,
Estimation procedure,
Degree of accuracy needed for the purpose described in the justification,
Unusual problems requiring specialized sampling procedures, and
Any use of periodic (less frequent than annual) data collection cycles to reduce burden.
This section discusses the procedures the contractor will use for impact estimation and the anticipated statistical power of the estimates.
The impact estimation approach will compare outcomes for the treatment group to a counterfactual estimate of what those outcomes would have been in the absence of the intervention. The contractor will use slightly different methods to estimate the counterfactuals for the various demonstration projects, depending on the evaluation design.
For demonstrations that use RA at the household level, the RA procedure should ensure that treatment and control households are equivalent, on average, in all respects other than participation in the intervention. Because the study’s primary outcome (food insecurity among children) is a binary variable, the contractor will use a logistic regression model to estimate project impacts. To test whether the results are sensitive to the modeling approach, a linear probability model will be used to estimate impacts on the primary outcome as an alternative.
The following model will be used to estimate the impacts of the demonstration in Nevada based on their two-arm household-level RA design1:
(1) 
where
y is the outcome of interest (such as food insecurity among
children) for household h,
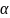 is
the regression intercept, T1 is a binary treatment indicator
for the first treatment arm that varies across households (set equal
to 1 for treatment households and 0 for control households), T2
is a binary indicator for the second treatment arm, X
represents a set or vector of household characteristics, β
is a vector of regression coefficients for those characteristics, and
ε is the regression’s residual. The parameters
of interest, δ1, which
represents the impact of the project for the first treatment arm (the
enhanced SNAP benefit), and δ2, which represents the
overall impact of enhanced benefits plus add-on services. The
difference between δ1 and δ2
represents the incremental impact of expanding the enhanced SNAP
benefits provided in the first treatment arm to include the
additional services offered in the second treatment arm, and the
contractor would test whether this difference was statistically
significant.
is
the regression intercept, T1 is a binary treatment indicator
for the first treatment arm that varies across households (set equal
to 1 for treatment households and 0 for control households), T2
is a binary indicator for the second treatment arm, X
represents a set or vector of household characteristics, β
is a vector of regression coefficients for those characteristics, and
ε is the regression’s residual. The parameters
of interest, δ1, which
represents the impact of the project for the first treatment arm (the
enhanced SNAP benefit), and δ2, which represents the
overall impact of enhanced benefits plus add-on services. The
difference between δ1 and δ2
represents the incremental impact of expanding the enhanced SNAP
benefits provided in the first treatment arm to include the
additional services offered in the second treatment arm, and the
contractor would test whether this difference was statistically
significant.
Under strong RA designs that identify equivalent treatment and control groups at baseline (via pairwise matching), it may not be necessary to include covariates in the regression model to produce unbiased impact estimates. However, controlling for the characteristics of sample respondents can help to improve the precision of the impact estimates if those characteristics are associated with the outcome of interest, in this case (primarily) food insecurity among children, and if these factors are related to sample attrition. The most important covariate will likely be baseline levels of the outcome measure. Other covariates in the model will include the number and composition of household members, urbanicity, and socioeconomic characteristics of the head of household, food shopping practices, meal preparation patterns, participation in other nutrition assistance programs, and child-level characteristics, such as race/ethnicity, age, and receipt of school-based meals.
The analysis will use respondent weights that correspond to the survey’s sampling design and adjust for survey nonresponse. The contractor will calculate standard errors using appropriate adjustments for these weighting factors and account for heteroskedasticity in the sample (that is, not assume that the amount of variance in the data is the same across subpopulations of survey respondents). With RA at the household level, the standard errors for model 1 will not need to be adjusted for clustering. Because the study will focus on a primary outcome specified in advance (food insecurity among children), it will not be necessary to perform a multiple-comparisons adjustment for the principal (confirmatory) impact estimates. However, to estimate impacts on the larger set of secondary (exploratory) outcomes, we will perform a multiple-comparisons correction that adjusts the p-values of statistical tests to correct for the chance that, with a large number of outcomes, some impacts may appear “significant” due to random variation in the sample.
In the remaining three demonstrations (Chickasaw Nation, Navajo Nation, and Virginia), we will use a design that requires RA at the level of geographic areas or sites such as schools or school districts. In these instances, the approach shown in model 1 will be adapted to account for the clustering of households (h) within sites (s) that are randomly assigned in a given project (j) (and that will also include just a single treatment arm) using the following model:
(2) 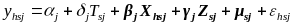
where
in this model T is a site-level treatment indicator. In
addition to controlling for a vector of individual and household
characteristics (X), this model will control for an additional set of
site-level characteristics (Z). For example, if the project randomly
selected food banks to receive support for new outreach activities,
the model would control for food bank characteristics (such as
location and size) that may be correlated with project implementation
and food insecurity or other outcomes. The standard errors for model
2 will account for the clustering of households within sites
(represented by the
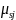 component of the error term); this will result in larger standard
errors (and a larger minimum detectable impact) than the model 1
estimates produced for household-level RA designs.
component of the error term); this will result in larger standard
errors (and a larger minimum detectable impact) than the model 1
estimates produced for household-level RA designs.
Some demonstrations may offer additional services to participants in an existing program. For example, Virginia will offer parents and guardians nutrition education services designed to help them use their household food budget efficiently to provide healthy meals. In these instances, there may be interest in both the impact of offering these services to potential beneficiaries and the impact of the services on the subset of treatment households that obtain them. For this type of intervention, the coefficient δj from model 2 would represent the overall impact of being offered the service, sometimes referred to as an intent-to-treat effect. To calculate the impact on the households that receive the service, the contractor will use an instrumental variables approach to estimate the effect of the treatment on the treated effect (also sometimes referred to as the complier average causal effect, or CACE). This approach uses the (randomly defined) treatment status variable as an instrument for obtaining the program treatment (Imbens and Angrist 1994).
For each demonstration project, the analysis will estimate impacts among subgroups of participants who may respond differently to the intervention. In particular, the analysis will estimate impacts on subgroups defined by (1) household structure (such as presence of three or more children in the household and presence of more than one adult in the household); (2) baseline food security status (food insecurity among children before the project); (3) race/ethnicity of the household respondent; (4) urban or rural status (in Virginia and in other sites, if possible); (5) education of the household respondent (such as less than high school, high school degree, or any postsecondary education); and (6) income (such as less than 100 percent of the federal poverty level). It will also examine whether impacts differ based on respondents’ participation in other nutrition assistance programs. For example, if an intervention was designed to encourage greater levels of participation in SNAP and other nutrition assistance programs, the analysis will estimate impacts for subgroups defined by respondents’ participation. The analysis will estimate a variant of model 1 separately for each subgroup, and will report impact estimates for those who are and are not in the subgroup and the magnitude and statistical significance of the difference between the two estimates.
The site-specific analyses will describe the characteristics of each demonstration site. Specifically, significance tests will be conducted to examine whether the impact estimates for each demonstration are statistically distinguishable.
Since the evaluation will have a small number of demonstration sites and their outcomes will be based on local conditions and implementation strategies, site-to-site comparative analysis has limited informative value; however, the analysis plan includes the preparation of descriptive statistics across all sites for general site-to-site comparative purposes. Such analyses will only be able to generate hypotheses about which intervention models or site characteristics may be related to impacts on food insecurity among children. To improve site-to-site comparisons, the analysis will attempt to use measures of each outcome across sites that take into account the design of the demonstration. This is especially important because the expected duration of exposure to SNAP benefits may vary across sites. For example, an intervention that delivers enhanced SNAP benefits may reach all participants immediately, whereas an intervention that encourages SNAP enrollment could lead treatment households to sign up for benefits at different times throughout the project implementation period. Across all demonstration projects, the evaluation will use a 30-day measure of household food insecurity and the classification scheme described by Nord and Coleman-Jensen (2014) to assess food insecurity among children, adults, and the household as a whole. We will account for the different lengths of SNAP exposure in comparing demonstration outcomes. We will also assess the 30-day food insecurity measure at a second follow-up for Chickasaw Nation, which has a longer implementation period.
For interventions evaluated with a cluster RA design, the analysis will also explore whether cluster-level characteristics are associated with project impacts. For example, for Virginia, we will examine whether impacts are different in clusters located in urban versus rural areas. For demonstrations with a second follow-up, we will compare results across all three periods to create a simple trend line.
To adequately address the evaluation’s research questions, the design must have sufficient statistical power to detect impacts that are policy relevant and of practical significance. The evaluation design will allow detection of policy-relevant impacts in each of the demonstration sites, overall and for key sample subgroups. The sample sizes needed for the study were determined by focusing on minimum detectable impacts (MDIs) for the key outcome of food insecurity among children and other key outcomes. In the three sites with a cluster design the sample sizes needed may not be obtainable given the projects’ approved grant plans and budgets. As a result the MDIs that will be obtainable are heavily dependent on the survey response rates. Table B.2.a provides a summary of the sample sizes planned for each project.
Table B.2.a. Summary of expected sample sizes per demonstration project
Grantee |
Intervention |
Design |
Number of clusters |
Starting sample size |
Chickasaw Nation |
1) Monthly home delivery of shelf-stable foods selected by project participants from a menu of options set by the project 2) A $15 cash voucher to purchase fresh fruits and vegetables from participating retailers will be mailed with the food package (above) to participants |
Cluster-level RCT (School Districts) |
40 |
4,750a |
Kentucky |
1) All eligible households will receive a fixed transportation deduction in the SNAP benefit determination formula. The size of the deduction will vary by county based on average distance from SNAP participants’ homes to the nearest grocery store
2) All eligible households who report any earned income will also receive an enhanced earned income deduction equal to 10 percent of earned income |
Single arm household-level RCT |
Not applicable |
4,504 |
Navajo Nation |
1) Community-based problem-solving, advocacy and technical assistance delivered by 12 food access navigators (FANs) (4 per intervention community/district) to increase availability of meals to school children through expansion of the NSLP, SBP (after the Bell), at-risk afterschool CACFP, and SFSP (may also include efforts to expand access to WIC)
2) Regional identification and coordination of assets, and supervision of FANs to be conducted by Regional FAN Supervisors, with one FAN supervisor per health district/intervention area.
3) Governance-level policy advocacy to be carried out by the FAN Director, the FAN Governance/Policy Coordinator, and the Project Liaison |
Cluster-level RCT (Tribal Chapters) |
34 |
5,750a |
Nevada |
1) Increase household SNAP benefits by $40 per month per eligible child ages 0-5 for 12 months.
2) Case management services to link families to all available federal nutrition programs and targeted education to increase healthy shopping habits. Specific education services (e.g. cooking classes, in-person training) will be determined once grantee learns what services participants are already receiving through other programs. |
Two arm HH-level RCT |
Not applicable |
6,746 |
Virginia |
1) Universal provision of three meals a day
2) Universal provision of food backpacks for weekends and winter and spring breaks
3) $60 monthly benefit during summer, per child eligible for SNAP or free/reduced-price meals
4) Nutrition education for parents/guardians |
Cluster-level RCT (Schools) |
40 |
4,750a |
a
Sample sizes are constrained in the cluster-level projects by the
number of participating school districts, schools, and Tribal
chapters and the number of eligible households in those clusters.
To identify a target MDI, we examined the impacts of similar programs in two prior FNS studies: the Summer Electronic Benefits Transfer for Children (SEBTC) evaluation (Collins et al. 2013; OMB Control Number 0584-0559, Discontinued 3/31/2014) and the study of the Supplemental Nutrition Assistance Program Participation on Food Security (SNAPFS) (Mabli et al. 2013; OMB Control Number 0584-0563, Discontinued 9/19/2011). Based on the impact estimates reported in these studies, the current study needs to be able to detect impacts as low as 10 to 15 percent. Estimates from the literature suggest that the study may find a baseline rate of food insecurity among children in the range of 30 to 50 percent. Thus, a 10 to 15 percent impact corresponds to an impact of 0.03 (10 percent of 30 percent) to 0.075 (15 percent of 50 percent). The target MDI has been set for the study at the midpoint of this range, or about 0.05 (5 percentage points). In other words, the target for this study is to be able to detect as statistically significant with high probability a true impact as low as 5 percentage points. The sample that allows us to detect this impact will also allow us to detect impacts for several subgroups (described below) that are above this target but still at or below the estimated SEBTC impact ($60 per eligible child per summer month).
Since the starting sample sizes in Table B.2.a are limited as noted previously we presented the MDI under two response rate assumptions to gauge the range of possible outcomes. The first set of MDI calculations is based on an assumed response rate of 80 percent. The second set of MDI calculations assumes a lower response rate of 60 percent. In both cases MDI calculations assume that the design will have a power level of 80 percent and use a 5 percent level of statistical significance. They also assume that a one-sided hypothesis will be tested: that participation in the intervention leads to a reduction in food insecurity among children. Several additional assumptions are required to calculate MDIs, and are based on published results or data analysis conducted from SNAPFS and the SEBTC study. These include (1) the base rate of food insecurity among children in the control group will be 0.40; and (2) an R-squared value of 0.20, meaning the impact model covariates will be able to explain 20 percent of the variation in the outcome measure. For clustered RA designs we also make assumptions about the number of clusters that are randomly assigned, which will vary based on the demonstration (more details below), and the intraclass correlation coefficient (ICC) for food insecurity among children, which we assume to be 0.008.
For the household-level RA design with two treatment arms, which will be implemented for Nevada, a total sample of 6,746 households will be selected (Exhibit B.2.a).2 With an 80 percent response rate (Exhibit B.2b), this will result in an expected analysis sample of about 2,937 households, or 979 in each of the two treatment arms and control group, and yield an MDI of 0.050 when comparing two of these groups. This design will also give substantial statistical power to detect impacts on food insecurity among children in key subgroups of households. For example, it can detect impacts as low as 8.4 percentage points (the estimated impact of the SEBTC $60 per child benefit) or lower for households that have children and have income below poverty, include a disabled member, include a single adult, have a white respondent, and are located in an urban area, among others. Other subgroups with small samples have somewhat larger MDIs, but the design can still detect moderate to large impacts (12 percentage points or fewer) on food insecurity among children in these subgroups. With a 60 percent response rate (Exhibit B.2c), the expected analysis sample would be about 1,650 households, or 550 in each of the two treatment arms and control group. The MDI would be about 0.067 when comparing two of these groups (a larger MDI than when an 80 percent response rate was assumed); MDIs for subgroups would be larger under this design assuming a 60 percent response rate than the MDIs when an 80 percent response rate is assumed.
Exhibit B.2b. Minimum detectable impacts in the Nevada project using household-level RA with two treatment arms, impacts on food insecurity among children (80% response rate)
Sample |
Available Sample |
Number of responding households at 12-Month Follow-up |
Number of responding households in treatment arm 1 at 12-Month Follow-up |
Number of responding households in treatment arm 2 at 12-Month Follow-up |
Number of responding households in control group at 12-Month Follow-up |
Minimum detectable impact |
Full sample |
6,746 |
2,937 |
979 |
979 |
979 |
0.050 |
Key subgroups |
|
|
|
|
|
|
Single adult HHs |
3,507 |
1,527 |
509 |
509 |
509 |
0.070 |
HHs with income below poverty |
4,722 |
2,055 |
685 |
685 |
685 |
0.060 |
|
|
|
|
|
|
|
Hispanic |
2,091 |
909 |
303 |
303 |
303 |
0.091 |
Black, Non-Hispanic |
1,215 |
528 |
176 |
176 |
176 |
0.119 |
White, Non-Hispanic |
2,832 |
1,233 |
411 |
411 |
411 |
0.078 |
Less than HS education |
1,821 |
792 |
264 |
264 |
264 |
0.097 |
HS degree, no college |
2,226 |
969 |
323 |
323 |
323 |
0.088 |
Some college or beyond |
2,697 |
1,173 |
391 |
391 |
391 |
0.080 |
Urban |
5,193 |
2,262 |
754 |
754 |
754 |
0.058 |
Non-urban |
1,553 |
675 |
225 |
225 |
225 |
0.105 |
Notes: These minimum detectable impacts assume 80% power and a 5% level of statistical significance. We assume that the overall prevalence of food insecurity among children is 40%, the response rate is 80% in both treatment arms and the control group, and the design effect due to weighting is 1.05. We also assume an R-squared value of 0.20 from covariates included in the impact model.
The assumptions about subgroup prevalence (which determine the subgroup sample sizes) are based on data from the SEBTC study (Collins et al. 2013) and the SNAP Food Security data (Mabli et al. 2013).
The race/ethnicity variable and educational attainment are for the respondent to the household survey.
Exhibit B.2c. Minimum detectable impacts in the Nevada project using household-level RA with two treatment arms, impacts on food insecurity among children (60% response rate)
Sample |
Starting Sample |
Number of responding households at 12-Month Follow-up |
Number of responding households in treatment arm 1 at 12-Month Follow-up |
Number of responding households in treatment arm 2 at 12-Month Follow-up |
Number of responding households in control group at 12-Month Follow-up |
Minimum detectable impact |
Full sample |
6,746 |
1,650 |
550 |
550 |
550 |
0.067 |
Key subgroups |
|
|
|
|
|
|
Single adult HHs |
3,507 |
858 |
286 |
286 |
286 |
0.094 |
HHs with income below poverty |
4,722 |
1,158 |
386 |
386 |
386 |
0.080 |
|
|
|
|
|
|
|
Hispanic |
2,091 |
510 |
170 |
170 |
170 |
0.121 |
Black, Non-Hispanic |
1,215 |
297 |
99 |
99 |
99 |
0.159 |
White, Non-Hispanic |
2,832 |
693 |
231 |
231 |
231 |
0.104 |
Less than HS education |
1,821 |
447 |
149 |
149 |
149 |
0.130 |
HS degree, no college |
2,226 |
546 |
182 |
182 |
182 |
0.117 |
Some college or beyond |
2,697 |
660 |
220 |
220 |
220 |
0.107 |
Urban |
5,193 |
1,272 |
424 |
424 |
424 |
0.077 |
Non-urban |
1,553 |
378 |
126 |
126 |
126 |
0.141 |
Notes: These minimum detectable impacts assume 80% power and a 5% level of statistical significance. We assume that the overall prevalence of food insecurity among children is 40%, the response rate is 60% in both treatment arms and the control group, and the design effect due to weighting is 1.05. We also assume an R-squared value of 0.20 from covariates included in the impact model.
The assumptions about subgroup prevalence (which determine the subgroup sample sizes) are based on data from the SEBTC study (Collins et al. 2013) and the SNAP Food Security data (Mabli et al. 2013).
The race/ethnicity variable and educational attainment are for the respondent to the household survey.
The remaining three awardees (Chickasaw Nation, Navajo Nation, and Virginia) will implement a clustered RA design in which a cluster of households is the unit of treatment assignment, rather than the individual household. Under this design, the similarity of households within each cluster reduces the efficiency of the sample, and likewise decreases the statistical precision to require a larger household sample to achieve the target MDI. A key aspect of this design is the number of clusters randomly assigned. In such designs, if more clusters are included the MDI may be achieved with a smaller overall analysis sample. Conversely, using fewer clusters requires a larger overall sample. For example, an RA design with 60 clusters could achieve an MDI of 0.05 with a total sample of 4,000 households. At 20 clusters, the required sample size would balloon to 8,500. Exhibits B.2d and B.2e shows sample sizes and MDIs under the cluster design we will implement in Virginia assuming response rates of 80 percent and 60 percent, respectively considering the actual number of schools that have agreed to participate. With an 80 percent response rate, an MDI of 0.05 is expected, while with a lower response rate of 60 percent, the MDI is expected to increase to about 0.058 for the full sample when comparing the treatment and control groups.
Exhibit B.2d. Minimum detectable impacts in the Virginia project using clustered random assignment with one treatment arm, impacts on food insecurity among children (80% response rate)
Sample |
Starting Sample |
Number of responding households |
Number of responding households in treatment arm 1 |
Number of responding households in control group |
Minimum detectable impact |
Full sample |
4,750 |
3,800 |
1,900 |
1,900 |
0.050 |
Key subgroups |
|
|
|
|
|
Single adult HHs |
2,470 |
1,976 |
988 |
988 |
0.061 |
HHs with income below poverty |
3,326 |
2,660 |
1,330 |
1,330 |
0.056 |
|
|
|
|
|
|
Hispanic |
1,472 |
1,178 |
589 |
589 |
0.074 |
Black, Non-Hispanic |
856 |
684 |
342 |
342 |
0.092 |
White, Non-Hispanic |
1,996 |
1,596 |
798 |
798 |
0.066 |
Less than HS education |
1,282 |
1,026 |
513 |
513 |
0.078 |
HS degree, no college |
1,568 |
1,254 |
627 |
627 |
0.072 |
Some college or beyond |
1,900 |
1,520 |
760 |
760 |
0.067 |
Urban |
3,658 |
2,926 |
1,463 |
1,463 |
0.054 |
Non-urban |
1,092 |
874 |
437 |
437 |
0.083 |
Notes: These minimum detectable impacts assume 80% power and a 5% level of statistical significance. We assume that the overall prevalence of food insecurity among children is 40%, the response rate is 80% in both treatment arms and the control group, and the design effect due to weighting is 1.05. We also assume an R-squared value of 0.20 from covariates included in the impact model, the overall sample is spread across 40 clusters, and an intraclass correlation coefficient (ICC) of 0.008.
The assumptions about subgroup prevalence (which determine the subgroup sample sizes) are based on data from the SEBTC study (Collins et al. 2013).
The race/ethnicity variable and educational attainment are for the respondent to the household survey.
Exhibit B.2e. Minimum detectable impacts in the Virginia project using clustered random assignment with one treatment arm, impacts on food insecurity among children (60% response rate)
Sample |
Starting Sample |
Number of responding households |
Number of responding households in treatment arm 1 |
Number of responding households in control group |
Minimum detectable impact |
Full sample |
4,750 |
2,850 |
1,425 |
1,425 |
0.058 |
Key subgroups |
|
|
|
|
|
Single adult HHs |
2,470 |
1,482 |
741 |
741 |
0.071 |
HHs with income below poverty |
3,326 |
1,996 |
998 |
998 |
0.064 |
|
|
|
|
|
|
Hispanic |
1,472 |
884 |
442 |
442 |
0.085 |
Black, Non-Hispanic |
856 |
514 |
257 |
257 |
0.106 |
White, Non-Hispanic |
1,996 |
1,198 |
599 |
599 |
0.076 |
Less than HS education |
1,282 |
770 |
385 |
385 |
0.090 |
HS degree, no college |
1,568 |
940 |
470 |
470 |
0.083 |
Some college or beyond |
1,900 |
1,140 |
570 |
570 |
0.078 |
Urban |
3,658 |
2,194 |
1,097 |
1,097 |
0.063 |
Non-urban |
1,092 |
656 |
328 |
328 |
0.096 |
Notes: These minimum detectable impacts assume 80% power and a 5% level of statistical significance. We assume that the overall prevalence of food insecurity among children is 40%, the response rate is 80% in both treatment arms and the control group, and the design effect due to weighting is 1.05. We also assume an R-squared value of 0.20 from covariates included in the impact model, the overall sample is spread across 40 clusters, and an intraclass correlation coefficient (ICC) of 0.008.
The assumptions about subgroup prevalence (which determine the subgroup sample sizes) are based on data from the SEBTC study (Collins et al. 2013).
The race/ethnicity variable and educational attainment are for the respondent to the household survey.
In Navajo Nation we will implement a design where 34 clusters of “Tribal chapters,” which are similar to counties, will be randomly assigned to treatment and control conditions. With 34 clusters, we will need approximately 5,750 households to achieve an MDI of 0.05 for the full respondent sample assuming an 80 percent response rate. Chickasaw Nation will randomly assign 40 schools to treatment and control conditions. To achieve an MDI of 0.05 for the full sample (assuming an 80 percent response rate) we will need to sample 4,750 households within these clusters, which should be possible given the eligible population being considered in Chickasaw Nation.
The samples described above are sufficient to detect impacts of a single intervention (demonstration project) on food insecurity among children as low as our target of 5 percentage points in most cases (assuming an 80 percent response rate). These samples will also allow the evaluation to detect policy-relevant impacts on the other outcomes examined as part of the study (Exhibits B.2.f and B.2.g). For example, the analysis will be able to detect project-specific impacts of about 3 percentage points in very low food security among children (for each type of design) assuming an 80 percent response rate, which is less than the estimated impact of SEBTC (Collins et al. 2013). MDIs for the other outcomes are all close to 5 percentage points or below (again, assuming an 80 percent response rate). For a continuous outcome, such as food expenditures or cup equivalents of fruits and vegetables, the MDI is about one-tenth of a standard deviation. If the standard deviation of monthly expenditures was $150, for example, the design could detect an impact as low as $15 per month. When the response rate is assumed to be 60 percent (Exhibit B.2.g) the MDIs are larger, but still allow for detection of policy-relevant impacts for these outcomes.
Exhibit B.2.f. Minimum detectable impacts on secondary outcomes (80% response rate)
Sample |
Starting sample |
Number of responding households |
Number of responding households in each treatment arm |
Number of responding households in control group |
Minimum detectable impact |
Nevada project using HH-level RA with two treatment arms—full samplea |
|||||
Secondary food security measures |
|
|
|
|
|
Very low food security—children |
6,746 |
2,937 |
979 |
979 |
0.030 |
Food insecurity—adults |
6,746 |
2,937 |
979 |
979 |
0.051 |
Very low food security—adults |
6,746 |
2,937 |
979 |
979 |
0.046 |
Food insecurity—households |
6,746 |
2,937 |
979 |
979 |
0.051 |
Very low food security—households |
6,746 |
2,937 |
979 |
979 |
0.047 |
Other outcomes |
|
|
|
|
|
Food expendituresb |
6,746 |
2,937 |
979 |
979 |
0.103 |
SNAP participation |
6,746 |
2,937 |
979 |
979 |
0.045 |
Virginia project using clustered RA with one treatment arm—full sample |
|||||
Secondary food security measures |
|
|
|
|
|
Very low food security—children |
4,750 |
3,800 |
1,900 |
1,900 |
0.030 |
Food insecurity—adults |
4,750 |
3,800 |
1,900 |
1,900 |
0.051 |
Very low food security—adults |
4,750 |
3,800 |
1,900 |
1,900 |
0.046 |
Food insecurity—households |
4,750 |
3,800 |
1,900 |
1,900 |
0.051 |
Very low food security—households |
4,750 |
3,800 |
1,900 |
1,900 |
0.047 |
Other outcomes |
|
|
|
|
|
Food expendituresb |
4,750 |
3,800 |
1,900 |
1,900 |
0.103 |
SNAP participation |
4,750 |
3,800 |
1,900 |
1,900 |
0.045 |
Source: These minimum detectable impacts assume 80% power and a 5% level of statistical significance. We assume that the overall prevalence of food insecurity among children is 40%, the response rate is 80% in both the treatment and control groups, and the design effect due to weighting is 1.10. We also assume an R-squared value of 0.20 from covariates included in the impact model.
The assumptions about subgroup prevalence (which determine the subgroup sample sizes) are based on data from the SEBTC study (Collins et al. 2013).
The race/ethnicity variable and educational attainment are for the respondent to the household survey.
a Nevada households will be randomly assigned to the treatment or control group following completion of the baseline survey. The sample sizes reflect the starting sample and assume rates of 85 percent eligibility, 80 percent consent, and 80 percent response, and account for households that could be eligible at the time of the baseline interview but exit SNAP pre-implementation and therefore become ineligible post-interview.
bThe MDI for food expenditures is reported in effect size units, or the proportion of the outcome's standard deviation.
Exhibit B.2.g. Minimum detectable impacts on secondary outcomes (60% Response Rate)
Sample |
Available Sample |
Number of responding households |
Number of responding households in each treatment arm |
Number of responding households in control group |
Minimum detectable impact |
Nevada project using HH-level RA with two treatment arms—full sample |
|||||
Secondary food security measures |
|
|
|
|
|
Very low food security—children |
6,746 |
1,650 |
550 |
550 |
0.040 |
Food insecurity—adults |
6,746 |
1,650 |
550 |
550 |
0.068 |
Very low food security—adults |
6,746 |
1,650 |
550 |
550 |
0.0.61 |
Food insecurity—households |
6,746 |
1,650 |
550 |
550 |
0.068 |
Very low food security—households |
6,746 |
1,650 |
550 |
550 |
0.063 |
Other outcomes |
|
|
|
|
|
Food expendituresa |
6,746 |
1,650 |
550 |
550 |
0.141 |
SNAP participation |
6,746 |
1,650 |
550 |
550 |
0.060 |
Virginia project using clustered RA with one treatment arm—full sample |
|||||
Secondary food security measures |
|
|
|
|
|
Very low food security—children |
4,750 |
2,850 |
1,425 |
1,425 |
0.035 |
Food insecurity—adults |
4,750 |
2,850 |
1,425 |
1,425 |
0.058 |
Very low food security—adults |
4,750 |
2,850 |
1,425 |
1,425 |
0.053 |
Food insecurity—households |
4,750 |
2,850 |
1,425 |
1,425 |
0.059 |
Very low food security—households |
4,750 |
2,850 |
1,425 |
1,425 |
0.055 |
Other outcomes |
|
|
|
|
|
Food expendituresa |
4,750 |
2,850 |
1,425 |
1,425 |
0.122 |
SNAP participation |
4,750 |
2,850 |
1,425 |
1,425 |
0.052 |
Source: These minimum detectable impacts assume 80% power and a 5% level of statistical significance. We assume that the overall prevalence of food insecurity among children is 40%, the response rate is 60% in both the treatment and control groups, and the design effect due to weighting is 1.10. We also assume an R-squared value of 0.20 from covariates included in the impact model.
The assumptions about subgroup prevalence (which determine the subgroup sample sizes) are based on data from the SEBTC study (Collins et al. 2013).
The race/ethnicity variable and educational attainment are for the respondent to the household survey.
aThe MDI for food expenditures is reported in effect size units, or the proportion of the outcome's standard deviation.
Additional households will be randomly selected and placed in holdout samples in sites that have large enough populations (or numbers of consented households) to accommodate additional sample. Households in holdout samples will only be released if we are experiencing low response rates in one or more sites during the course of data collection and do not expect to meet the target number of completes with the original sample. The households in the holdout samples will be randomly ordered for release and households will be released to help reach the target number of completes.
B.3. Methods to maximize response rates and deal with nonresponse
Describe methods to maximize response rates and to deal with issues of non-response. The accuracy and reliability of information collected must be shown to be adequate for intended uses. For collections based on sampling, a special justification must be provided for any collection that will not yield "reliable" data that can be generalized to the universe studied.
Below describes procedures that will be used to achieve the target response rate, including gaining sample members’ cooperation and locating hard-to-reach demonstration participants.
Methods to gain cooperation:
Contractor’s technical assistants will help awardees explain the importance of the demonstration and participating in household surveys. Awardees will be available to answer questions and will use community resources to spread information about the demonstration and facilitate recruiting.
Contractor will mail advance letters to sample members before the baseline and follow-up surveys, and mail reminder letters and refusal conversion letters to those who have not completed interviews.
Within a week after the advance letter mailing, if a respondent has not called in to complete the interview, the contractor will begin contacting them by phone to complete the survey. The contractor will accept calls to their call center at any time. As such there is at most a one week delay between the mail notification and a phone attempt.
To help explain the study to potential participants and add legitimacy, FNS, awardees, and the contractor will collaborate to design a website for the study. The contractor will also produce glossy site-specific brochures to help explain the study to potential participants.
The contractor will have a toll-free number and study email address that demonstration participants may call at their convenience to ask questions, schedule an appointment, or complete the interview.
The contractor will offer a $30 incentive to demonstration participants for the household surveys.
The contractor will make multiple calls to participants at different times of the day and days of the week to increase the likelihood of reaching participants when they are available.
The contractor will send refusal conversion letters to those who mildly refuse to participate. Interviewers skilled in refusal conversion will make second attempts to address concerns and complete the interview.
Potential participants in the Chickasaw Nation and Navajo Nation demonstration areas may be less inclined to participate in the study due to factors such as a lack of trust in outside researchers or limited access to telephone service. The contractor will collaborate with awardees and with Tribal leadership to gain important endorsements of the study and work together to determine the best ways to conduct outreach to reservation-based households. When possible, the contractor will employ members of the Indian Tribal Organization as telephone interviewers and field locators.
Methods to locate hard-to-reach demonstration participants:
Where possible, awardees will collect physical and email addresses and multiple phone numbers and provide this information to the contractor.
For individuals without current telephone information, the contractor will attempt to obtain this information from vendor databases. For more difficult cases, the contractor will conduct more intensive individual searches.
The contractor will collect contact information at baseline and the first follow-up to facilitate reaching sample members for the next survey, including permission to send text messages to cellular phones and contact information for someone who does not live with the participant who would know how to reach him or her for the next interview.
For the follow-up interviews, the contractor will employ field locators to find demonstration participants who cannot be reached by telephone.
Throughout each round of data collection, the contractor will use production reports to monitor response rates and missing data for each awardee, for treatment and control groups. The contractor will monitor paradata and adapt the data collection appropriately to yield a high response rate. For example, the contractor can determine the most productive calling windows based on monitoring of completed surveys during the early data collection period, and adapt the staffing plan to maximize interviewer efficiency.
B.4. Description of tests of procedures
Describe any tests of procedures or methods to be undertaken. Testing is encouraged as an effective means of refining collections of information to minimize burden and improve utility. Tests must be approved if they call for answers to identical questions from 10 or more respondents. A proposed test or set of tests may be submitted for approval separately or in combination with the main collection of information.
The EDECH household surveys rely largely on instruments and items that have been fielded in previous studies. The contractor consequently focused on new questions and overall administrative time and flow. The contractor recruited eight adults through community organizations that serve low-income households with children. Two were Spanish-speaking. The survey was administered by telephone or, in one case, in-person. Based on the amount of time it took to complete each interview as well as pretest participants’ feedback, the contractor deleted several items from the surveys and limited additional questions to specific demonstration sites.
B.5. Individuals consulted on statistical aspects of the design
Provide the name and telephone number of individuals consulted on statistical aspects of the design and the name of the agency unit, contractor(s), awardee(s), or other person(s) who will actually collect and/or analyze the information for the agency.
The information will be collected and analyzed by Mathematica Policy Research. The sampling procedures were developed by Nicholas Beyler (telephone 202-250-3539) of Mathematica. The sampling plans were reviewed internally by Michael Sinclair (telephone 202-552-6439), a senior fellow at Mathematica. Audra Zakzeski (telephone 703-877-8000) of the National Agricultural Statistics Service (NASS) has also reviewed this supporting statement and provided comments that have been incorporated.
Burghardt, John A., Philip M. Gleason, Michael Sinclair, Rhoda Cohen, Lara K. Hulsey, and Julita Milliner-Waddell. “Evaluation of the National School Lunch Program Application/Verification Pilot Projects: Volume I: Impacts on Deterrence, Barriers, and Accuracy.” Princeton, NJ: Mathematica Policy Research, 2004.
Collins, Ann M., Ronette Briefel, Jacob Alex Klerman, Gretchen Rowe, Anne Wolf, Christopher W. Logan, Anne Gordon, Carrie Wolfson, Ayesha Enver, Cheryl Owens, Charlotte Cabili, and Stephen Bell. “Summer Electronic Benefits Transfer for Children (SEBTC) Demonstration: Evaluation Findings for the Full Implementation Year.” Final report submitted to the U.S. Department of Agriculture, Food and Nutrition Service. Cambridge, MA: Abt Associates, July 2013.
Imai, Kosuke, Gary King, and Clayton Nall. “The Essential Role of Matching in Cluster-Randomized Experiments, with Application to the Mexican Universal Health Insurance Evaluation.” Statistical Science, vol. 24, no. 1, 2009, pp. 29–53.
Imbens, Guido W., and Joshua D. Angrist. “Identification and Estimation of Local Average Treatment Effects.” Econometrica, vol. 62, no. 2, March 1994.
Kauff, Jacqueline, Lisa Dragoset, Elizabeth Clary, Elizabeth Laird, Libby Makowsky, and Emily Sama-Miller. “Reaching the Underserved Elderly and Working Poor in SNAP: Evaluation Findings from the Fiscal Year 2009 Pilots.” Final report submitted to the U.S. Department of Agriculture, Food and Nutrition Service. Washington, DC: Mathematica Policy Research, April 2014.
Mabli, James, Jim Ohls, Lisa Dragoset, Laura Castner, and Betsy Santos. “Measuring the Effect of Supplemental Nutrition Assistance Program (SNAP) Participation on Food Security.” Cambridge, MA: Mathematica Policy Research, 2013.
Nord, Mark, and Alisha Coleman-Jensen. “Improving food security classification of households with children.” Journal of Hunger & Environmental Nutrition, vol. 9(3), 2014, pp. 318-333.
1 The model in Kentucky, with household-level RA to a single treatment arm, will be similar to equation (1) except that it will include just one rather than two treatment indicators.
2 In Kentucky, with its household-level RA design with a single treatment arm, a total sample of 4,504 will be selected. The resulting MDIs will be similar to those reported in Exhibits B.2b and B.2c for Nevada.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | Evaluation of Demonstration Projects to End Childhood Hunger, Part B: Collections of Information Employing Statistical Methods |
| Subject | OMB Statement |
| Author | Mathematica Staff |
| File Modified | 0000-00-00 |
| File Created | 2021-01-25 |
© 2026 OMB.report | Privacy Policy