ED Response to OMB Passback
HSLS 2009 2nd Follow-up Main Study Response to Passback.docx
High School Longitudinal Study of 2009 (HSLS:09) Second Follow-up Main Study and 2018 Panel Maintenance
ED Response to OMB Passback
OMB: 1850-0852
Memorandum United States Department of Education
Institute of Education Sciences
National Center for Education Statistics
DATE: December 14, 2015
TO: Robert Sivinski, OMB
THROUGH: Kashka Kubzdela, OMB Liaison, NCES
FROM: Elise Christopher, HSLS:09 Project Officer, NCES
SUBJECT: High School Longitudinal Study of 2009 (HSLS:09) Second Follow-up Main Study and 2018 Panel Maintenance (1850-0852 v.17) Responses to OMB Passback
This memorandum provides responses to OMB questions regarding responsive design plans for main study package for the High School Longitudinal Study of 2009 (HSLS:09) Second Follow-up.
Comment: You need a probability or likelihood qualifier here, if we knew for sure we wouldn’t need the survey.
Associated text (B.4.c): We will do so by selectively targeting for special interventions a subset of cases that would most contribute to nonresponse bias if they did not respond.
NCES: Wording has been revised in section B.4.c as follows: “We will do so by selectively targeting for special interventions a subset of cases that might contribute most to potential nonresponse bias if they do not respond.”
Comment: Consider improving the clarity of this statement.
Associated text (B.4.c): Can we better represent the population of interest (i.e., fall 2009 9th graders as of 2016) by including cases in the respondent pool we may not have otherwise been successful pursuing (sample representativeness)?
NCES: Wording has been revised in section B.4.c as follows: “Can the responding sample better represent the population of interest (i.e., fall 2009 9th graders as of 2016) by gaining participation from sample members whose characteristics differ from current respondents and who otherwise might not respond (sample representativeness)?”
Comment: Sample representativeness can be an indicator of bias, but the two are often conflated. A simulation like this seems like a good opportunity to test whether increased representativeness led to significant changes in any of the key outcome variables.
Associated text (B.4.c): Sample representativeness. The field test sample size does not allow us to answer the questions definitively but the simulations allow us to test procedures and analyze the results as if the responsive design model was used. To address the first question, we produced estimates of sample allocation versus respondent allocation for certain variables that were part of the responsive design model. Exhibit B-4 shows a small number of example sample-representativeness measures. As can be seen, the respondent percentages at the end of data collection were closer to the overall sample percentages than respondents prior to phase 4, as represented by the given values shown in exhibit B-4. For example, Hispanics comprised 3.7 percent of the field test sample. Before phase 4, Hispanics represented only 2.8 percent of the responding sample, but the percentage grew to 3.5 by the end of data collection. As another example, students from high schools in the Midwest comprised 19.0 percent of the field test sample. The responding sample percentage was 22.9 percent prior to phase 4, 21.8 percent prior to phase 5, and 20.8 percent at the end of field test data collection.
NCES: We agree that sample representativeness and nonresponse bias are often conflated. Our focus on sample representativeness is targeted to maximize the alignment of the responding sample to the population, not knowing a priori how the respondents will answer the survey questions – and therefore not knowing whether increased sample representativeness will result in significant changes in any of the key outcome variables. The numbers of sample members and respondents in the field test do not have sufficient power to detect potential differences in variables, given that the response rate differences did not reach the level of statistical significance. We will examine the results from the calibration sample (which also has an experimental design) in the main study, to see if we are able to observe any patterns with outcome variables. (This response is a clarification; no associated changes to Part B were made.)
Comment: For the response and bias likelihood models, do you have already constructed models using previously collected data? Do you have technical reports on these models?
Associated text (B.4.d): Response Likelihood Model. The response likelihood model will be run only once, before data collection begins. Using data obtained in prior waves that are correlated with response outcome (primarily paradata variables), we will fit a model predicting response outcome in the 2013 Update. We will then use the coefficients associated with the significant predictors to estimate the likelihood of response in the second follow-up main study, and each sample member will be assigned a likelihood score prior to the start of data collection. Exhibit B-10 lists the universe of predictor variables that will be considered for the response likelihood model.
NCES: For reference, we have attached excerpts from HSLS:09 and ELS:2002 Data File Documentation (DFDs) that describe responsive design models and results (please note that some of the formatting, equations, etc. got lost in conversion when copied into this memo; the provided URL for the DFDs and the section numbers indicate where to find the original information in the source DFDs.). The following sentence has been added to the end of the “Model development” section of B.4.d: “The models for the HSLS:09 second follow-up main study have been developed and will be refined from models for previous rounds of HSLS:09, ELS:2002, and other NCES studies, including BPS:12/14.”
[Excerpt taken from: High School Longitudinal Study of 2009 (HSLS:09) 2013 Update and High School Transcript Data File Documentation. http://nces.ed.gov/pubs2015/2015036.pdf]
Responsive Design Methodology
The following section describes the responsive design methodology that provided a plan for maintaining bias-minimizing response rates.
Implementation and evaluation of the responsive design plan for targeting nonrespondents: selection methodology. The 2013 Update responsive design methodology consisted of seven phases (see section 2.3.2 above) that provided a plan to (1) target sample members identified as ever having dropped out of school,
(2) calculate response propensities to select cases for incentives at several points during collection, and (3) offer abbreviated and PAPI questionnaires to all nonrespondents. Targeted cases included underrepresented, nonresponding cases whose survey estimates after completing a questionnaire would likely be different from those who responded.
The propensity model developed for the 2013 Update data collection incorporated both survey variables and demographic variables from prior rounds. The dependent variable for all propensity models was survey outcome (i.e., response or nonresponse) at the time that the model was run. The goal of the model was not to maximize the ability to predict the survey outcome. Rather, the goal was to use a prediction of the likelihood to participate in order to identify nonresponding cases who may reduce nonresponse bias if interviewed.
The models excluded paradata (e.g., such as the number of call attempts or the number of refusals during the 2013 Update data collection) and other variables that were highly predictive of response but unrelated to the survey estimates of interest. Using survey estimates in the models required using single imputations to provide missing values for model variables. After imputing missing values, the distributions of the model estimates were examined and categories collapsed when cell sizes were less than 4 percent.

The same logistic regression was performed before the start of phases 3, 4, and 5. Because the study targeted those cases that were found to be the least likely to participate in the 2013 Update, many of the same cases were targeted in each phase.
Evaluation of targeting methods and intervention effectiveness. This section reviews the effectiveness of the responsive design model used to target cases for incentives during data collection. The results of the responsive design approach on survey estimates and nonresponse bias can be found in chapter 6. That chapter presents weighted and unweighted key survey estimates and estimates of nonresponse bias for each variable used in the model:
 𝑦𝑦
𝑦𝑦
− 𝑦𝑦
 �
𝑟𝑟
�
𝑟𝑟


 𝑦𝑦𝑠𝑠
𝑦𝑦𝑠𝑠
𝑠𝑠�
where
yr is the respondent mean and
ys is the sample mean.
Model effectiveness. The responsive design approach requires that nonresponding cases be identified with survey responses that are underrepresented among the respondents. The tables in appendix M show each model variable and the proportion of cases within four groups, by phase: (1) the entire sample, (2) the set of respondents by phase, (3) the nonresponding cases selected for intervention, and
the nonresponding cases not selected for intervention.
The general pattern across all model variables indicates that the model effectively selected cases who were underrepresented among the respondents. For example, table 1 in appendix M shows the phase 3 breakdown across the model variables. The timing of the Algebra 1 variable is illustrative of the general trend. In the entire sample:
30.7 percent took Algebra 1 in 8th grade;
56.8 percent took Algebra 1 in 9th grade;
8.4 percent took Algebra 1 in 10th grade; and
4.2 percent took Algebra 1 in 11th or 12th grades or did not take Algebra 1. Among respondents at the start of phase 3:
39.2 percent took Algebra 1 in 8th grade;
49.8 percent took Algebra 1 in 9th grade;
7.4 percent took Algebra 1 in 10th grade; and
3.6 took Algebra 1 in 11th or 12th grades or did not take Algebra 1.
If the model effectively targeted cases, we should see these differences among the targeted set of cases.
Among the respondents at the start of phase 5:
35.1 percent took Algebra 1 in 8th grade;
53.1 percent took Algebra 1 in 9th grade;
8.0 percent took Algebra 1 in 10th grade; and
3.8 took Algebra 1 in 11th or 12th grades or did not take Algebra 1.
Changes in this survey estimate between the start of phase 3 and the start of phase 5 appear to move in the direction of the estimates for the entire sample. These results suggest that targeted cases did account for discrepancies between the entire sample and the set of respondents.
Intervention effectiveness. The responsive design plan specified an intervention for each phase to increase participation. The intervention in each phase included a different combination of treatments, which included (1) prepaid incentives, (2) promised incentives, and (3) an increased dollar amount of promised incentives. Because a control group was not included in the research design, it is not possible to conduct
an experimental analysis of the responsive design plan. However, cases not targeted with incentives can serve as a baseline for the pattern of response over the course of the data collection. During data collection, disproportionate increases in the response rates of targeted cases would help to identify effective intervention strategies. While smaller increases in response rates were expected in later phases, overall participation among targeted cases was expected to increase with each phase relative to nontargeted cases, which only received outbound telephone calls.
Table 6 displays participation rates during each phase by ever-dropout, nontargeted, targeted, and previously targeted cases. The highest participation rates for both ever- dropout cases (34 percent) and nontargeted cases (31 percent) occurred during phase
2. As seen in table 6, the lowest participation rate for three of the four categories occurred during phase 5. This may be an unintended consequence of the partial government shutdown, which began less than 2 weeks after the start of phase 5.
Excluding cases identified as ever having dropped out of school, targeted cases became incentivized during phases 3, 4, 5, and 6. Table 6 demonstrates that targeted cases had higher participation rates than nontargeted cases in each phase besides phase 3. The highest participation rate occurred during phase 6 (26 percent), and the lowest rate occurred during phase 3 (16 percent).

 CHAPTER
2.
CHAPTER
2.
 2013
UPDATE
INSTRUMENTATION,
SAMPLE
DESIGN,
AND
DATA
COLLECTION 35
2013
UPDATE
INSTRUMENTATION,
SAMPLE
DESIGN,
AND
DATA
COLLECTION 35
Phase |
cases1, 2 |
N |
% |
N |
% |
of cases |
N |
% |
of cases |
N |
% |
of cases |
N |
% |
of cases |
N |
% |
1 |
23,415 |
3,700 |
15.8 |
3,700 |
15.8 |
1,974 |
490 |
24.8 |
21,441 |
1,210 |
15.0 |
† |
† |
† |
† |
† |
† |
2 |
19,715 |
6,207 |
31.5 |
9,907 |
42.3 |
1,484 |
497 |
33.5 |
18,231 |
5,710 |
31.3 |
† |
† |
† |
† |
† |
† |
3 |
13,508 |
2,585 |
19.1 |
12,492 |
53.4 |
987 |
280 |
28.4 |
6,183 |
1,267 |
20.5 |
6,338 |
1,038 |
16.4 |
† |
† |
† |
4 |
10,923 |
2,213 |
20.3 |
14,705 |
62.8 |
707 |
120 |
17.0 |
4,845 |
1,000 |
20.6 |
4,731 |
991 |
21.0 |
640 |
102 |
15.9 |
5 |
8,710 |
1,181 |
13.6 |
15,886 |
67.8 |
587 |
82 |
14.0 |
3,777 |
412 |
10.9 |
3,627 |
603 |
16.6 |
719 |
84 |
11.7 |
6 |
7,529 |
1,547 |
20.6 |
17,433 |
74.5 |
505 |
87 |
17.2 |
1,357 |
257 |
18.9 |
2,706 |
710 |
26.2 |
2,961 |
493 |
16.6 |
7 |
5,982 |
1,125 |
18.8 |
18,558 |
79.3 |
418 |
65 |
15.6 |
1,100 |
227 |
20.6 |
† |
† |
† |
4,464 |
833 |
18.7 |
HSLS:09 2013 UPDATE AND HIGH SCHOOL TRANSCRIPT DATA FILE DOCUMENTATION
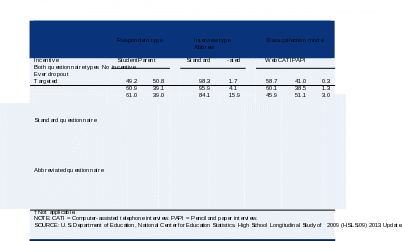 Table
7
shows
response
outcomes
for
standard
(full-length)
and
abbreviated
questionnaires
by
student
and
parent
respondents
and
data
collection
mode.
Overall,
about
62
percent
of
standard
questionnaires
were
completed
by
student
sample
members
for
ever-dropout
cases
and
targeted
incentive
cases.
However,
the
proportion
of
parent
and
student
respondents
completing
a
questionnaire
was
about
the
same
when
no
incentive
was
offered.
Table
7
shows
response
outcomes
for
standard
(full-length)
and
abbreviated
questionnaires
by
student
and
parent
respondents
and
data
collection
mode.
Overall,
about
62
percent
of
standard
questionnaires
were
completed
by
student
sample
members
for
ever-dropout
cases
and
targeted
incentive
cases.
However,
the
proportion
of
parent
and
student
respondents
completing
a
questionnaire
was
about
the
same
when
no
incentive
was
offered.
-
No incentive
49.2
50.8
†
†
59.3
40.7
†
Ever dropout
61.6
38.4
†
†
61.5
38.5
†
Targeted
61.5
38.5
†
†
48.4
51.6
†
-
No incentive
46.5
53.5
†
†
28.7
55.4
16.0
Ever dropout
46.5
53.5
†
†
27.9
39.4
32.8
Targeted
58.0
42.0
†
†
32.3
48.8
18.9
As noted in section 2.3.3, cases with a student who had ever dropped out of high school were offered an incentive of $40 to complete a questionnaire for the 2013 Update. Table 8 presents unweighted participation rates for cases who had ever dropped out of high school, were offered no incentive, and were targeted for an incentive during one of the seven data collection phases (see section 2.3.3). At the end of data collection, cases who had ever dropped out of school had an 82 percent unweighted participation rate. The unweighted participation rate for all other completed cases besides the ever-dropout cases was 78 percent.
-
Table 8. Summary of 2013 Update participation rates for dropout cases, cases who were not offered an incentive, and targeted cases: 2013
Unweighted All cases1 Completed participation rates
Total 23,401 18,558 79.3
Dropout 1,973 1,621 82.2
No incentive2 12,951 12,083 93.3
Targeted 8,477 4,854 57.3
1 An additional 88 cases who participated in either the base year or first follow-up study were excluded from the 2013 Update sample because their status was deceased, ineligible, or a study withdrawal. However, these 88 cases are included on 2013 Update data files because prior-round response data exist for these cases.
2 New cases received an incentive offer at the start of phase 1, 3, 4, 5, or 6 (see section 2.3.3). A total of 1,100 nonresponding cases were never offered an incentive during data collection.
SOURCE: U.S. Department of Education, National Center for Education Statistics, High School Longitudinal Study of 2009 (HSLS:09) 2013 Update.
6.3 Assessment of Responsive Design
The responsive design approach, which was based on approaches used in previous National Center for Education Statistics (NCES) studies, aims to reduce nonresponse bias in survey estimates by targeting sample members who are most unlike the current responding cases. The responsive design approach was not implemented as an experimental design; therefore, there are no treatment and control groups to compare to assess the effects on nonresponse bias. Instead,
responsive design was assessed by examining if (1) cases that were targeted and responded at each phase were different from the existing respondents on key estimates; (2) key estimates calculated at phase 3 (the start of the responsive design case targeting) were different from the estimates calculated at the conclusion of data collection; and (3) estimates shifted by targeting were more like population estimates on variables known for all sample members (i.e., demographics). If key estimates did not change between phase 3 and the conclusion of data collection, the participation of targeted cases likely had little influence on the final survey estimates for key variables.
The variables examined in this analysis are shown in table 33. Table 34 shows these variable estimates37 from the 2013 Update student survey across different data collection phases. A way to understand how targeting nonrespondents might work would be to look at the distribution of select survey estimates prior to targeting and post-targeting. Therefore, in table 34, the column “Overall estimate at the start of phase 3” shows the distribution prior to targeting and the column “Final survey estimate” shows the distribution after targeting. The concept would be that the targeted cases are important to include because their survey responses differ from those of the nontargeted cases. In looking at the distribution of estimates across the table, a contention is that targeting results in a different final distribution than would have otherwise resulted without targeting. Take, for example, the characteristic “Taking postsecondary classes.” The weighted estimate for the percentage of students taking postsecondary classes at the beginning of phase 3 was 87.59 percent. At the start of phases 4 and 5, the percent taking postsecondary classes estimates for targeted cases appears to be much lower than those for nontargeted cases, which suggests that the targeted set may have indeed been different on this variable.
Furthermore, the nontargeted set of cases appear to be very similar to respondents on this characteristic, suggesting that the targeting approach identified cases that were different from respondents even for key variables not included in the targeting model. At the conclusion of data collection, the final estimate for the percent taking postsecondary classes fell nearly 10 percentage points from the estimate calculated at the start of phase 3 (87.59 percent to 77.73 percent). This suggests that targeting the cases resulted in a final distribution that was markedly different from the distribution at the end of phase 3. In other words, the case-targeting approach appears to have changed the estimate over the course of data collection. In general, these analyses suggest that targeting cases as a strategy for nonresponse follow-up can be an

37 Estimates weighted by the student base weight. For purposes of these comparisons, no adjustments were made for differential nonresponse.
effective approach for identifying nonresponding cases who differ from existing respondents on key survey variables.
Next, it is important to examine if case targeting through the responsive design approach could bring survey estimates more in line with true population estimates through targeting nonresponding cases that differ from respondents on key survey variables. Because population estimates are not available for survey items, some variables known for all sample members were incorporated into the analyses in order to provide some population estimates against which estimates for targeted, nontargeted, and targeted plus nontargeted respondents could be compared.
Race/ethnicity and sex variables were examined. On the race/ethnicity variable, phase 3 estimates, for example, were higher for Whites and lower for Blacks and Hispanics than the population estimates. However, by the end of data collection, the final estimates changed to more closely reflect the population estimates. So on the race/ethnicity variable, the targeting approach does appear to have brought estimates more in line with the population. Over time, changes for sex appear to be less obviously affected.
-
Table 33. 2013 Update key variables examined
Variable Label
S3HSCRED Teenager has high school credential
S3CLASSES) Taking postsecondary classes
S3APPRENTICE Apprenticing
S3CURWORK Currently working for pay
S3MILITARY Serving in the military
S3FAMILY Starting family/taking care of children
S3HS Attending high school or homeschool
S3GEDCOURSE In a course to prepare for GED
S3APPFAFSA Completed a Free Application for Student Aid (FAFSA) X2RACE Student’s race/ethnicity
X2SEX Student’s sex
SOURCE: U.S. Department of Education, National Center for Education Statistics. High School Longitudinal Study of 2009 (HSLS:09) 2013 Update.
Table 34. |
Weighted estimates of key 2013 Update variables, by data collection phase |
|||||
Variable |
Overall estimate at the start of phase 3 |
Overall estimate at the start of phase 4 Non- Targeted targeted respondents respondents |
All cases |
Overall estimate at the start of phase 5 Non- Targeted targeted respondents respondents |
All cases |
Final survey estimate |
Teenager has earned a high school credential |
|
|
|
|
|
|
Yes |
90.72 |
83.10 91.70 |
90.51 |
86.10 90.55 |
90.18 |
89.09 |
No |
9.28 |
16.90 8.30 |
9.49 |
13.90 9.45 |
9.82 |
10.91 |
Taking posts |
econdary classes |
|
|
|
|
|
Yes |
87.59 |
71.16 88.11 |
85.99 |
62.94 85.80 |
84.11 |
77.73 |
No |
12.41 |
28.84 11.89 |
14.01 |
37.06 14.20 |
15.89 |
22.27 |
Apprenticing |
as of Nov. 1, 2013 |
|
|
|
|
|
Yes |
2.85 |
7.82 2.91 |
3.56 |
8.06 3.45 |
3.83 |
3.91 |
No |
97.15 |
92.18 97.09 |
96.44 |
91.94 96.55 |
96.17 |
96.09 |
Working for pay as of Nov. 1, 2013 |
|
|
|
|
|
|
Yes |
63.24 |
79.29 62.59 |
64.98 |
77.26 64.66 |
65.76 |
64.70 |
No |
36.76 |
20.71 37.41 |
35.02 |
22.74 35.34 |
34.24 |
35.30 |
Serving in the military as of Nov. 1, 2013 |
|
|
|
|
|
|
Yes |
4.61 |
4.40 4.34 |
4.35 |
5.73 4.30 |
4.42 |
4.13 |
No |
95.39 |
95.60 95.66 |
95.65 |
94.27 95.70 |
95.58 |
95.87 |
Starting famil |
y/taking care of children as of |
|
|
|
|
|
Nov. 1, 2 |
013 |
|
|
|
|
|
Yes |
3.87 |
10.37 3.59 |
4.51 |
12.21 4.56 |
5.19 |
6.19 |
No |
96.13 |
89.63 96.41 |
95.49 |
87.79 95.44 |
94.81 |
93.81 |
See notes at end of table.
Table 34. |
Weighted estimates of key 2013 Update variables, by data collection phase—Continued |
|||||
Variable |
Overall estimate at the start of phase 3 |
Overall estimate at the start of phase 4 Non- Targeted targeted respondents respondents |
All cases |
Overall estimate at the start of phase 5 Non- Targeted targeted respondents respondents |
All cases |
Final survey estimate |
Did not comp |
lete FAFSA because teen does not |
|
|
|
|
|
plan to continue education |
|
|
|
|
|
|
Yes |
19.42 |
23 18.32 |
19.16 |
27.53 19.08 |
20.02 |
22.12 |
No |
80.58 |
77 81.68 |
80.84 |
72.47 80.92 |
79.98 |
77.88 |
Currently wor |
king for pay |
|
|
|
|
|
Yes |
50.8 |
45.94 51.85 |
51.04 |
44.43 50.24 |
49.75 |
50.02 |
No |
49.2 |
54.06 48.15 |
48.96 |
55.57 49.76 |
50.25 |
49.98 |
SOURCE: U.S. Department of Education, National Center for Education Statistics. High School Longitudinal Study of 2009 (HSLS:09) 2013 Update, Restricted-use Data File and |
||||||
Control System Data. |
||||||

Table 35. Weighted estimates of race/ethnicity and sex by phase and compared with population estimates |
|||||||||
Race/ethnicity and sex |
Overall estimate at the start of phase 3 |
Overall estimate at the start of phase 4 |
Overall estimate at the start of phase 5 |
Final survey estimate |
Population estimate |
||||
Targeted respondent |
Nontargeted respondents |
All cases |
Targeted respondent |
Nontargeted respondents |
All cases |
||||
Race/ethnicity American Indian/Alaska Native, non- Hispanic Asian, non- Hispanic Black/African- American, non-Hispanic Hispanic, no race specified Hispanic, race specified More than one race, non- Hispanic Native Hawaiian/Pa cific Islander, non-Hispanic White, non- Hispanic
Sex Male Female |
0.50
4.42
8.60
1.10
17.06
6.85
0.50
60.98
49.87 50.13 |
1.15
2.51
20.71
3.83
29.33
5.99
0.44
36.04
54.31 45.69 |
0.44
4.68
8.35
0.95
16.46
6.83
0.47
61.82
49.57 50.43 |
0.54
4.38
10.06
1.35
18.24
6.71
0.47
58.26
50.23 49.77 |
0.58
2.02
28.41
2.57
27.17
8.29
0.35
30.62
49.63 50.37 |
0.54
4.37
10.00
1.25
17.83
6.85
0.45
58.70
49.87 50.13 |
0.55
4.17
11.56
1.36
18.63
6.98
0.44
56.32
49.85 50.15 |
0.70
3.60
13.49
1.76
20.48
7.40
0.51
52.07
50.51 49.49 |
.69
3.70
13.93
2.56
20.02
7.23
.49
51.38
50.77 49.23 |
SOURCE: U.S. Department of Education, National Center for Education Statistics. High School Longitudinal Study of 2009 (HSLS:09) 2013 Update, Restricted-use Data File and Control System Data. |
|||||||||
[Excerpt taken from: Education Longitudinal Study of 2002 (ELS:2002) Third Follow-Up Data File Documentation. http://nces.ed.gov/pubs2014/2014364.pdf]
Responsive Design Methodology
Responsive Design for ELS:2002 Third Follow-up Nonresponse Follow-up
NCES and RTI are researching new strategies for conducting more effective nonresponse follow-up during the data collection period. There is a general recognition in the survey literature that nonresponse follow-up should be a strategic activity that prioritizes cases with the goal of minimizing bias in the final survey estimates (see for example, Peytchev et al. 2010; Rosen et al. 2011; Wagner 2012). Furthermore, there is strong evidence that the overall survey response rate is an inadequate measure of data quality (e.g., Curtin et al. 2000; Groves and Peytcheva 2008; Keeter et al. 2000). The greatest danger in nonresponse follow-up may be when a study brings in sample members who resemble those most likely to respond or those who have already responded (Schouten, Cobben, and Bethlehem 2009). Under this scenario, resources are spent on increasing participation, but little is done to minimize bias. Decreasing bias during the nonresponse follow-up depends on the cases that are ultimately interviewed (Peytchev, Baxter, and Carley-Baxter 2009). The critical factor is that nonresponding cases selected for targeting should be substantively different from the respondent set at any one point during data collection. The question remains how to go about selecting those cases.
In the ELS:2002 third follow-up, a responsive design (Groves and Heeringa 2006) was implemented in an attempt to minimize nonresponse bias. The following sections describe the implementation approach.
Responsive Design Approach
The goal of the responsive design is to identify and target, via specific protocols or interventions, the nonresponding cases that are different from the respondent set at any one point. Although numerous approaches are available to identify cases (i.e., critical subgroups, propensity to respond), the ELS:2002 third follow-up used a Mahalanobis distance function to identify nonrespondent cases most unlike the existing respondent set. A large number of survey variables, paradata, and sampling frame variables were incorporated into the distance function calculation, providing an opportunity to target the cases most unlike respondents and therefore, if completed, most likely to reduce nonresponse bias.
Following Li and Valliant (2009), the Mahalanobis Distance (MD) may be defined as:
𝑛𝑤� ℎ𝑖𝑖
𝑀𝐷 =
− 1
 𝑤𝑖
𝑤𝑖
where hii is the leverage (hat diagonal) for the ith case, wi is the sample weight for the ith case, n is the number of cases or observations, and 𝑤 is the average sample weight. The hat diagonals are the diagonal elements of the hat matrix (H):
𝐻 = (𝑋𝑇𝑊𝑋)−1𝑋𝑇𝑊
where W is a diagonal matrix of sample weights and X is a matrix of variables that define the dimensions along which distances are calculated.
In the context of its use in the ELS:2002 third follow-up, Mahalanobis distance is defined as the distance between a nonresponding case and the weighted mean value of the complete set of responding cases. Therefore, cases with larger distance scores can be thought of as cases demonstrating large differences from the respondent set. That is, these large distance cases would be characterized by larger differences in the input variables from the weighted means of the variables for respondents. Identifying these cases and presenting the specifically targeted nonresponding cases with a higher incentive will in turn attempt to boost their participation and potentially reduce bias in estimates and also improve analytic power through higher sample sizes for these groups of cases of analytic interest.
A distance function was calculated at three points during data collection:
right before outbound CATI began, 4 weeks into data collection;
right before the CAPI period began, 9 weeks into data collection; and
just prior to the prepaid incentive period, approximately 8 weeks prior to the end of data collection.
At these points, the cases with the largest distance scores were offered a $55 incentive while the $25 base incentive remained intact for all other cases (not including ever dropout cases, which were offered $55 to complete the survey from the start of data collection). At each juncture, the cases identified for targeting were those with the largest distance scores but not targeted in the prior phase(s). At the third and final case selection point, cases identified for targeting received a $5 prepaid incentive in addition to the $55 incentive and other nonmonetary activities, such as enhanced tracing. Case targeting was based on distance scores and the anticipated yield. At the first intervention point, 1,169 cases were targeted; at the second point, 2,390 cases were targeted; and at the third point, 1,721 cases were targeted. At each of these points, the Mahalanobis values were calculated and targeted cases were selected.
Mahalanobis Model Specification
Variable Selection. Choosing variables to include in the distance function calculation is an important process. The goal is to identify variables that are (1) known for respondents and nonrespondents, and (2) important analytically so that bias in the final survey estimates would be problematic. Table 14 shows the variables used in calculating the Mahalanobis distance.
Table
14. Variables
used
in
the
Mahalanobis
calculation
in
the
third
follow-up:
2012

 Frame
variables Survey
variables Paradata1
Frame
variables Survey
variables Paradata1
School control
(public, Catholic, other private)
School urbanicity (urban, suburban, rural)
Parent’s highest level of education
High school transcript-reported cumulative GPA
Whether English is student’s native language
Ever earned GED/equivalency
Sex
Socioeconomic status
Diploma or certificate most likely to receive
Took or plans to take SAT or ACT
Took or plans to take Advanced Placement test
F1 enrollment status
Highest level of education respondent expects to complete
F1 sample member in-school grade-level status
F2 response status
F1 nonresponse type
Ever responded to a panel maintenance
F2 call count
Number of contact attempts
Response status for F3 panel maintenance
F1 and BY combined response status

1 Paradata refers to data surrounding the survey interviewing process.
NOTE: BY = base year. F1 = first follow-up. F2 = second follow-up. F3 = third follow-up. GED = General Educational Development credential. GPA = grade point average.
SOURCE: U.S. Department of Education, National Center for Education Statistics. Education Longitudinal Study of 2002 (ELS:2002) Base Year to Third Follow-up, and Common Core of Data/Private School Survey.
Technical Issues With Mahalanobis Calculation. Multiple approaches are available for generating Mahalanobis distance scores. The initial approach for the phase 1 calculations was to take advantage of the close relationship between the leverage statistic and the Mahalanobis distance. Distance scores were generated for phase 1 by outputting the hat matrix from an ordinary least squares regression (unweighted), which forced into the regression all the variables of interest. In other words, no insignificant variables were dropped. From the hat diagonal value, the Mahalanobis distance was generated for each case. Upon further examination of this approach, it was apparent that the method used for generating scores compared nonrespondents to the full sample. Because the approach seeks to identify nonresponding cases that differ from the existing respondent set, the phase 1 approach was modified for use in phase 2.
For the phase 2 distance calculations, the approach was adjusted to ensure a comparison between nonrespondents and the existing set of respondents. For this, a Stata program called Mahascore (Kantor 2006) was used. Before implementation, it was confirmed that the Mahascore program was calculating Mahalanobis scores in a theoretically justifiable manner by determining that, in test cases, the produced scores matched the scores defined in Li and Valliant (2009). The Li and Valliant method for calculating Mahalanobis scores that incorporate sampling weights was implemented in the R programming language and applied to sets of test data. The Mahascore program was also applied to the test data and the resulting Mahalanobis scores were compared to these scores produced using the Li and Valliant method. The Mahalanobis scores produced using Mahascore matched the scores produced using the Li and Valliant method.
Several other technical issues arose. Using the Stata Mahascore program, categorical variables have to be represented as binary variables. Some input variables that had all derived binary variables included in the Mahascore program (no reference or dropped category) did not end up contributing to the calculation of the Mahalanobis scores. In sum, these variables were not accounted for in the final distance score. It was then necessary to analyze the selected cases when binary variables were handled appropriately. A post-case selection analysis was performed and it was determined that 95 percent of the selected cases would have been selected if the binary variables had been properly handled in Mahascore. The second issue involved small cell sizes in the respondent set of cases. Small cell sizes among respondents resulted in the inability to invert the variance-covariance matrix calculated from just respondent data and therefore the final Mahalanobis score could not include those variables. Refer to section 4.4 for response rates by responsive design group and chapter 6 for a discussion of the results of the responsive design in relation to bias scores.
Base-year to Third Follow-up Response Rates
Response rates for ELS:2002 are calculated by dividing the number of sample units who completed a particular study component by the number of sample units eligible for participation that are fielded. Sample members are not eligible if they are classified as deceased, sampling errors, or temporarily out of scope (unavailable for duration of study, out of the country, ineligible, incarcerated, or institutionalized). Eligible (in-scope) cases who were not contacted for participation (i.e., unfielded cases) are not counted in the response rate. All weighted response rates are calculated using the base weight appropriate for a given survey.15 For each round of data collection, nonresponse bias analyses were performed to ensure that any identified biases resulting from nonresponse were small or were adjusted for, and that the data could be used with confidence. Response rate data for ELS:2002 are summarized in table 15.

15 For example, the third follow-up used the first follow-up design weight adjusted for unknown eligibility and scope.

Twenty-eight of the variables had a least one statistically significant bias. The only variable that did not have any statistically significant bias was F3A08 (STATE IN WHICH GED/EQUIVALENCY WAS EARNED). There were 201 significant bias tests out of the 406 tests that were conducted.
Assessment of Responsive Design for ELS:2002 Third Follow-up
Responsive Design Setting
As discussed in section 4.3, the goal of responsive design was to identify and target, via new protocols or interventions, the nonresponding cases that are different from the respondent set at any one point. Although numerous approaches are available to identify target cases (e.g., critical subgroups, propensity to respond), the ELS:2002 third follow-up used a Mahalanobis distance function to identify nonrespondent cases most unlike the existing respondent set. A large number of survey variables, paradata, and sampling frame variables were incorporated into the distance function calculation providing an opportunity to target the cases most unlike respondents and therefore, if completed, most likely to reduce nonresponse bias. In this section, the bias results are discussed.
Responsive Design Results
Responsive design was integrated into the ELS:2002 third follow-up data collection and the responsive design is discussed in section 4.3. The analysis of the responsive design implementation is presented in this section. Cases that were selected at each of the phases had different levels of response. Those selected in phase 1 had an unweighted response rate of 72.9 percent. The cases selected in phase 2 had an unweighted response rate of 68.5 percent. The phase 3 cases had an unweighted response rate of 71.5 percent.
The primary question is whether data collection outcomes (i.e., bias in key survey estimates) were improved by identifying and prioritizing cases using a Mahalanobis distance score. To answer this question, 12 key frame and survey variables (the same variables used in the distance function calculation) were examined for evidence of bias at multiple points in data collection. The 12 variables included a total of 57 levels and therefore 57 bias estimates are presented. There were 4,683 cases that responded just before phase 1 case selection.
Cumulatively, 7,805 cases had responded before phase 2 case selection. Although there were 3,122 additional respondents between phase 1 case selection and phase 2 case selection, only 322 were phase 1 selected cases.
Table J-1 in appendix J lists the variables used to construct bias estimates and Table J-2 shows the categorization of those variables used in the bias assessment. Table J-3 shows the bias estimates for all respondents, untreated respondents, and untreated plus phase 1 respondents. At the conclusion of data collection, 35 of the 57 pre weight adjustment estimates are biased or have values statistically different from zero. If all respondents who received no treatment or were not targeted are considered, 41 of the 57 estimates are significantly different from zero, or biased. Finally, if the untreated plus phase 1 respondents are considered, 33 of 57 estimates are significantly biased. The number of biased estimates goes down slightly if respondents selected in phase 1 are included with the untreated respondents.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | Memorandum United States Department of Education |
| Author | audrey.pendleton |
| File Modified | 0000-00-00 |
| File Created | 2021-01-23 |
© 2025 OMB.report | Privacy Policy
