Attachment H - DW Source and Accuracy Statement
Attachment H-Displaced Workers-Source&Accuracy.docx
Displaced Worker, Job Tenure, and Occupational Mobility Supplement to CPS
Attachment H - DW Source and Accuracy Statement
OMB: 1220-0104
1
MEMORANDUM FOR: Lisa Clement
Survey Director for CPS & Time Use
Associate Directorate for Demographic Programs
From: James B. Treat
Chief, Demographic Statistical Methods Division
Subject: Source and Accuracy Statement for the January 2016 CPS Microdata File on Displaced Workers, Employee Tenure, and Occupational Mobility
Attached is the statement on the source of the data and accuracy of the estimates for the January 2016 CPS Microdata File on Displaced Workers, Employee Tenure, and Occupational Mobility.
If you have any questions or need additional information, please contact Rebecca Hoop of the Demographic Statistical Methods Division via email at [email protected].
Attachment
cc:
Kyra Linse (ADDP)
Tim Marshall
Mary Beth Eldridge
James Farber (DSMD)
Yang Cheng
Jimmie Scott
David Hornick
Rebecca Hoop
Nghiep Huynh
Anne E. Johnson
1Source of the Data and Accuracy of the Estimates for the
January 2016 CPS Microdata File on Displaced Workers, Employee Tenure, and Occupational Mobility
Table of Contents
SOURCE OF THE DATA 1
Basic CPS 1
January 2016 Supplement 2
Estimation Procedure 2
ACCURACY OF THE ESTIMATES 3
Sampling Error 3
Nonresponse 4
Sufficient Partial Interview 4
Coverage 4
Comparability of Data 5
A Nonsampling Error Warning 6
Standard Errors and Their Use 6
Estimating Standard Errors 7
Generalized Variance Parameters 7
Standard Errors of Estimated Numbers 8
Standard Errors of Estimated Percentages 9
Standard Errors of Estimated Differences 10
Standard Errors of Estimated Medians 11
Standard Errors of Quarterly or Yearly Averages 14
Technical Assistance 14
REFERENCES 16
Tables
Table 1. CPS Coverage Ratios: January 2016 5
Table 2. Estimation Groups of Interest and Generalized Variance Parameters 8
Table 3. Parameters for Computation of Standard Errors for Labor Force Characteristics:
January 2016 15
1Source of the Data and Accuracy of the Estimates for the
January 2016 CPS Microdata File on Displaced Workers, Employee Tenure, and Occupational Mobility
SOURCE OF THE DATA
The data in this microdata file are from the January 2016 Current Population Survey (CPS). The U.S. Census Bureau conducts the CPS every month, although this file has only January data. The January survey uses two sets of questions, the basic CPS and a set of supplemental questions. The CPS, sponsored jointly by the Census Bureau and the U.S. Bureau of Labor Statistics, is the country’s primary source of labor force statistics for the entire population. The Census Bureau and the Bureau of Labor Statistics also jointly sponsor the supplemental questions for January.
1Basic CPS. The monthly CPS collects primarily labor force data about the civilian noninstitutionalized population living in the United States. The institutionalized population, which is excluded from the population universe, is composed primarily of the population in correctional institutions and nursing homes (98 percent of the 4.0 million institutionalized people in Census 2010). Interviewers ask questions concerning labor force participation about each member 15 years old and over in sample households. Typically, the week containing the nineteenth of the month is the interview week. The week containing the twelfth is the reference week (i.e., the week about which the labor force questions are asked).
The CPS uses a multistage probability sample based on the results of the decennial census, with coverage in all 50 states and the District of Columbia. The sample is continually updated to account for new residential construction. When files from the most recent decennial census become available, the Census Bureau gradually introduces a new sample design for the CPS.
Every ten years the CPS first stage sample is redesigned 1 reflecting changes based on the most recent decennial census. In the first stage of the sampling process, primary sampling units (PSUs)2 were selected for sample. In the 2000 design, the United States was divided into 2,025 PSUs. These were then grouped into 824 strata and one PSU was selected for sample from each stratum. In the 2010 sample design, the United States was divided into 1,987 PSUs. These PSUs were then grouped into 852 strata. Within each stratum, a single PSU was chosen for the sample, with its probability of selection proportional to its population as of the most recent decennial census. In the case of strata consisting of only one PSU, the PSU was chosen with certainty.
In April 2014, the Census Bureau began phasing out the 2000 sample and replaced it with the 2010 sample, creating a mixed sampling frame. Two simultaneous changes occurred during this phase-in period. First, within the PSUs selected for both the 2000 and 2010 designs, sample households from the 2010 design gradually replaced sample households from the 2000 design. Second, new PSUs selected for only the 2010 design gradually replaced outgoing PSUs selected for only the 2000 design. By July 2015, the new 2010 sample design was completely implemented and the sample came entirely from the 2010 redesigned sample.
Approximately 74,000 housing units were selected for sample from the sampling frame in January. Based on eligibility criteria, 11 percent of these housing units were sent directly to computer-assisted telephone interviewing (CATI). The remaining units were assigned to interviewers for computer-assisted personal interviewing (CAPI).3 Of all housing units in sample, about 61,000 were determined to be eligible for interview. Interviewers obtained interviews at about 53,000 of these units. Noninterviews occur when the occupants are not found at home after repeated calls or are unavailable for some other reason.
1January 2016 Supplement. In January 2016, in addition to the basic CPS questions, interviewers asked supplementary questions of about displacement of workers, employee tenure, and occupational mobility. Questions concerning displaced workers were asked of all respondents who were at least 20 years old, and questions concerning job tenure and occupational mobility were asked of all employed respondents who were at least 15 years old.
1Estimation
Procedure. This survey’s estimation procedure adjusts
weighted sample results to agree with independently derived
population estimates of the civilian noninstitutionalized population
of the United States and each state (including the District of
Columbia). These population estimates, used as controls for the CPS,
are prepared monthly to agree with the most current set of population
estimates that are released as part of the Census Bureau’s
population estimates and projections program.
The population controls for the nation are distributed by demographic characteristics in two ways:
Age, sex, and race (White alone, Black alone, and all other groups combined).
Age, sex, and Hispanic origin.
The population controls for the states are distributed by race (Black alone and all other race groups combined), age (0-15, 16-44, and 45 and over), and sex.
The independent estimates by age, sex, race, and Hispanic origin, and for states by selected age groups and broad race categories, are developed using the basic demographic accounting formula whereby the population from the 2010 Census data is updated using data on the components of population change (births, deaths, and net international migration) with net internal migration as an additional component in the state population estimates.
The net international migration component of the population estimates includes:
Net international migration of the foreign born;
Net migration between the United States and Puerto Rico;
Net migration of natives to and from the United States; and
Net movement of the Armed Forces population to and from the United States.
Because the latest available information on these components lags the survey date, it is necessary to make short-term projections of these components to develop the estimate for the survey date.
1ACCURACY OF THE ESTIMATES
A sample survey estimate has two types of error: sampling and nonsampling. The accuracy of an estimate depends on both types of error. The nature of the sampling error is known given the survey design; the full extent of the nonsampling error is unknown.
Sampling Error. Since the CPS estimates come from a sample, they may differ from figures from an enumeration of the entire population using the same questionnaires, instructions, and enumerators. For a given estimator, the difference between an estimate based on a sample and the estimate that would result if the sample were to include the entire population is known as sampling error. Standard errors, as calculated by methods described in “Standard Errors and Their Use,” are primarily measures of the magnitude of sampling error. However, they may include some nonsampling error.
Nonsampling Error. For a given estimator, the difference between the estimate that would result if the sample were to include the entire population and the true population value being estimated is known as nonsampling error. There are several sources of nonsampling error that may occur during the development or execution of the survey. It can occur because of circumstances created by the interviewer, the respondent, the survey instrument, or the way the data are collected and processed. For example, errors could occur because:
• The interviewer records the wrong answer, the respondent provides incorrect information, the respondent estimates the requested information, or an unclear survey question is misunderstood by the respondent (measurement error).
• Some individuals who should have been included in the survey frame were missed (coverage error).
• Responses are not collected from all those in the sample or the respondent is unwilling to provide information (nonresponse error).
• Values are estimated imprecisely for missing data (imputation error).
• Forms may be lost, data may be incorrectly keyed, coded, or recoded, etc. (processing error).
To minimize these errors, the Census Bureau applies quality control procedures during all stages of the production process including the design of the survey, the wording of questions, the review of the work of interviewers and coders, and the statistical review of reports.
Two types of nonsampling error that can be examined to a limited extent are nonresponse and undercoverage.
Nonresponse. The effect of nonresponse cannot be measured directly, but one indication of its potential effect is the nonresponse rate. For the January 2016 basic CPS, the household-level nonresponse rate was 13.3 percent. The person-level nonresponse rate for the Displaced Workers, Employee Tenure, and Occupational Mobility supplement was an additional 8.3 percent.
Since the basic CPS nonresponse rate is a household-level rate and the Displaced Workers, Employee Tenure, and Occupational Mobility supplement nonresponse rate is a person-level rate, we cannot combine these rates to derive an overall nonresponse rate. Nonresponding households may have fewer persons than interviewed ones, so combining these rates may lead to an overestimate of the true overall nonresponse rate for persons for the Displaced Workers, Employee Tenure, and Occupational Mobility supplement.
In accordance with Census Bureau and Office of Management and Budget Quality Standards, the Census Bureau will conduct a nonresponse bias analysis to assess nonresponse bias in the Displaced Workers, Employee Tenure, and Occupational Mobility.
Sufficient Partial Interview. A sufficient partial interview is an incomplete interview in which the household or person answered enough of the questionnaire for the supplement sponsor to consider the interview complete. The remaining supplement questions may have been edited or imputed to fill in missing values. Insufficient partial interviews are considered to be nonrespondents. Refer to the supplement overview attachment in the technical documentation for the specific questions deemed critical by the sponsor as necessary to be answered in order to be considered a sufficient partial interview.
As part of the nonsampling error analysis, the item response rates, item refusal rates, and edits are reviewed. For the Displaced Workers, Employee Tenure, and Occupational Mobility supplement, the item refusal rates range from 0.0 percent to 5.9 percent. The item nonresponse rates range from 0.0 percent to 100 percent.
1Coverage. The concept of coverage in the survey sampling process is the extent to which the total population that could be selected for sample “covers” the survey’s target population. Missed housing units and missed people within sample households create undercoverage in the CPS. Overall CPS undercoverage for January 2016 is estimated to be about 11 percent. CPS coverage varies with age, sex, and race. Generally, coverage is larger for females than for males and larger for non-Blacks than for Blacks. This differential coverage is a general problem for most household-based surveys.
1The CPS weighting procedure partially corrects for bias from undercoverage, but biases may still be present when people who are missed by the survey differ from those interviewed in ways other than age, race, sex, Hispanic origin, and state of residence. How this weighting procedure affects other variables in the survey is not precisely known. All of these considerations affect comparisons across different surveys or data sources.
1A common measure of survey coverage is the coverage ratio, calculated as the estimated population before poststratification divided by the independent population control. Table 1 shows January 2016 CPS coverage ratios by age and sex for certain race and Hispanic groups. The CPS coverage ratios can exhibit some variability from month to month.
Table 1. CPS Coverage Ratios: January 2016 |
|||||||||||
|
Total |
White only |
Black only |
Residual race |
Hispanic |
||||||
Age group |
All people |
Male |
Female |
Male |
Female |
Male |
Female |
Male |
Female |
Male |
Female |
0-15 |
0.89 |
0.89 |
0.89 |
0.93 |
0.92 |
0.78 |
0.77 |
0.82 |
0.82 |
0.85 |
0.84 |
16-19 |
0.87 |
0.87 |
0.87 |
0.89 |
0.91 |
0.79 |
0.78 |
0.79 |
0.74 |
0.84 |
0.88 |
20-24 |
0.77 |
0.75 |
0.79 |
0.78 |
0.84 |
0.62 |
0.64 |
0.71 |
0.70 |
0.72 |
0.78 |
25-34 |
0.82 |
0.79 |
0.85 |
0.83 |
0.89 |
0.62 |
0.74 |
0.76 |
0.76 |
0.73 |
0.86 |
35-44 |
0.90 |
0.88 |
0.92 |
0.91 |
0.95 |
0.78 |
0.84 |
0.81 |
0.84 |
0.79 |
0.86 |
45-54 |
0.91 |
0.90 |
0.91 |
0.93 |
0.94 |
0.81 |
0.84 |
0.76 |
0.79 |
0.82 |
0.86 |
55-64 |
0.93 |
0.92 |
0.95 |
0.93 |
0.96 |
0.84 |
0.89 |
0.85 |
0.87 |
0.75 |
0.84 |
65+ |
0.96 |
0.95 |
0.97 |
0.96 |
0.98 |
0.91 |
0.97 |
0.86 |
0.79 |
0.85 |
0.82 |
15+ |
0.89 |
0.87 |
0.91 |
0.90 |
0.94 |
0.77 |
0.83 |
0.79 |
0.79 |
0.78 |
0.85 |
0+ |
0.89 |
0.88 |
0.90 |
0.90 |
0.93 |
0.77 |
0.81 |
0.80 |
0.80 |
0.80 |
0.85 |
Notes: (1) The Residual race group includes cases indicating a single race other than White or Black,
and cases indicating two or more races.
Hispanics may be any race. For a more detailed discussion on the use of parameters for
race and ethnicity, please see the “Generalized Variance Parameters” section.
1Comparability of Data. Data obtained from the CPS and other sources are not entirely comparable. This results from differences in interviewer training and experience and in differing survey processes. This is an example of nonsampling variability not reflected in the standard errors. Therefore, caution should be used when comparing results from different sources.
Data users should be careful when comparing the data from this microdata file, which reflects Census 2010-based controls, with microdata files from January 2003 through December 2011, which reflect 2000 census-based controls. Ideally, the same population controls should be used when comparing any estimates. In reality, the use of the same population controls is not practical when comparing trend data over a period of 10 to 20 years. Thus, when it is necessary to combine or compare data based on different controls or different designs, data users should be aware that changes in weighting controls or weighting procedures can create small differences between estimates. See the discussion following for information on comparing estimates derived from different controls or different sample designs.
Microdata files from previous years reflect the latest available census-based controls. Although the most recent change in population controls had relatively little impact on summary measures such as averages, medians, and percentage distributions, it did have a significant impact on levels. For example, use of Census 2010-based controls results in about a 0.2 percent increase from the 2000 census-based controls in the civilian noninstitutionalized population and in the number of families and households. Thus, estimates of levels for data collected in 2012 and later years will differ from those for earlier years by more than what could be attributed to actual changes in the population. These differences could be disproportionately greater for certain population subgroups than for the total population.
Users should also exercise caution because of changes caused by the phase-in of the Census 2010 files (see “Basic CPS”).4 During this time period, CPS data were collected from sample designs based on different censuses. Two features of the new CPS design have the potential of affecting published estimates: (1) the temporary disruption of the rotation pattern from August 2014 through June 2015 for a comparatively small portion of the sample, and (2) the change in sample areas. Most of the known effect on estimates during and after the sample redesign will be the result of changing from 2000 to 2010 geographic definitions. Research has shown that the national-level estimates of the metropolitan and nonmetropolitan populations should not change appreciably because of the new sample design. However, users should still exercise caution when comparing metropolitan and nonmetropolitan estimates across years with a design change, especially at the state level.
Caution should also be used when comparing Hispanic estimates over time. No independent population control totals for people of Hispanic origin were used before 1985.
1A Nonsampling Error Warning. Since the full extent of the nonsampling error is unknown, one should be particularly careful when interpreting results based on small differences between estimates. The Census Bureau recommends that data users incorporate information about nonsampling errors into their analyses, as nonsampling error could impact the conclusions drawn from the results. Caution should also be used when interpreting results based on a relatively small number of cases. Summary measures (such as medians and percentage distributions) probably do not reveal useful information when computed on a subpopulation smaller than 75,000.
For additional information on nonsampling error including the possible impact on CPS
data when known, refer to references [2] and [3].
1Standard Errors and Their Use. 1The sample estimate and its standard error enable one to construct a confidence interval. A confidence interval is a range about a given estimate that has a specified probability of containing the average result of all possible samples. For example, if all possible samples were surveyed under essentially the same general conditions and using the same sample design, and if an estimate and its standard error were calculated from each sample, then approximately 90 percent of the intervals from 1.645 standard errors below the estimate to 1.645 standard errors above the estimate would include the average result of all possible samples.
1A particular confidence interval may or may not contain the average estimate derived from all possible samples, but one can say with specified confidence that the interval includes the average estimate calculated from all possible samples.
1Standard errors may also be used to perform hypothesis testing, a procedure for distinguishing between population parameters using sample estimates. The most common type of hypothesis is that the population parameters are different. An example of this would be comparing the percentage of men who were part-time workers to the percentage of women who were part-time workers.
1Tests may be performed at various levels of significance. A significance level is the probability of concluding that the characteristics are different when, in fact, they are the same. For example, to conclude that two characteristics are different at the 0.10 level of significance, the absolute value of the estimated difference between characteristics must be greater than or equal to 1.645 times the standard error of the difference.
1The Census Bureau uses 90-percent confidence intervals and 0.10 levels of significance to determine statistical validity. Consult standard statistical textbooks for alternative criteria.
1Estimating Standard Errors. The Census Bureau uses replication methods to estimate the standard errors of CPS estimates. These methods primarily measure the magnitude of sampling error. However, they do measure some effects of nonsampling error as well. They do not measure systematic biases in the data associated with nonsampling error. Bias is the average over all possible samples of the differences between the sample estimates and the true value.
1Generalized Variance Parameters. While it is possible to compute and present an estimate of the standard error based on the survey data for each estimate in a report, there are a number of reasons why this is not done. A presentation of the individual standard errors would be of limited use, since one could not possibly predict all of the combinations of results that may be of interest to data users. Additionally, data users have access to CPS microdata files, and it is impossible to compute in advance the standard error for every estimate one might obtain from those data sets. Moreover, variance estimates are based on sample data and have variances of their own. Therefore, some methods of stabilizing these estimates of variance, for example, by generalizing or averaging over time, may be used to improve their reliability.
1Experience has shown that certain groups of estimates have similar relationships between their variances and expected values. Modeling or generalizing may provide more stable variance estimates by taking advantage of these similarities. The generalized variance function is a simple model that expresses the variance as a function of the expected value of the survey estimate. The parameters of the generalized variance function are estimated using direct replicate variances. These generalized variance parameters provide a relatively easy method to obtain approximate standard errors for numerous characteristics. In this source and accuracy statement, Table 3 provides the generalized variance parameters for labor force estimates and estimates from the January 2016 supplement.
The basic CPS questionnaire records the race and ethnicity of each respondent. With respect to race, a respondent can be White, Black, Asian, American Indian and Alaskan Native (AIAN), Native Hawaiian and Other Pacific Islander (NHOPI), or combinations of two or more of the preceding. A respondent’s ethnicity can be Hispanic or non-Hispanic, regardless of race.
The generalized variance parameters to use in computing standard errors are dependent upon the race/ethnicity group of interest. The following table summarizes the relationship between the race/ethnicity group of interest and the generalized variance parameters to use in standard error calculations.
Table 2. Estimation Groups of Interest and Generalized Variance Parameters |
|
Race/ethnicity group of interest |
Generalized variance parameters to use in standard error calculations |
Total population |
Total or White |
White alone, White AOIC, or White non-Hispanic population |
Total or White |
Black alone, Black AOIC, or Black non-Hispanic population |
Black |
Asian alone, Asian AOIC, or Asian non-Hispanic population |
Asian, AIAN, NHOPI |
AIAN alone, AIAN AOIC, or AIAN non-Hispanic population |
|
NHOPI alone, NHOPI AOIC, or NHOPI non-Hispanic population |
|
Populations from other race groups |
Asian, AIAN, NHOPI |
Hispanic population |
Hispanic |
Two or more races – employment/unemployment and educational attainment characteristics |
Black |
Two or more races – all other characteristics |
Asian, AIAN, NHOPI |
Notes: (1) AIAN is American Indian and Alaska Native and NHOPI is Native Hawaiian and Other Pacific Islander.
AOIC is an abbreviation for alone or in combination. The AOIC population for a race group of interest includes people reporting only the race group of interest (alone) and people reporting multiple race categories including the race group of interest (in combination).
Hispanics may be any race.
Two or more races refers to the group of cases self-classified as having two or more races.
Standard Errors of Estimated Numbers. The approximate standard error, sx, of an estimated number from this microdata file can be obtained by using the formula:
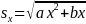 (1)
(1)
1Here x is the size of the estimate and a and b are the parameters in Table 3 associated with the particular type of characteristic. When calculating standard errors from cross-tabulations involving different characteristics, use the set of parameters for the characteristic that will give the largest standard error.
1Illustration 1
Suppose there were 4,087,000 unemployed men (ages 16 and up) in the civilian labor force. Use the appropriate parameters from Table 3 and Formula (1) to get
Illustration 1 |
|
Number of unemployed males in the civilian labor force (x) |
4,087,000 |
a parameter (a) |
-0.000031 |
b parameter (b) |
2,947 |
Standard error |
107,000 |
90-percent confidence interval |
3,911,000 to 4,263,000 |
The standard error is calculated as
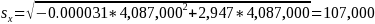
1The 90-percent confidence interval is calculated as 4,087,000 ± 1.645 × 107,000.
1A conclusion that the average estimate derived from all possible samples lies within a range computed in this way would be correct for roughly 90 percent of all possible samples.
1Standard Errors of Estimated Percentages. The reliability of an estimated percentage, computed using sample data for both numerator and denominator, depends on both the size of the percentage and its base. Estimated percentages are relatively more reliable than the corresponding estimates of the numerators of the percentages, particularly if the percentages are 50 percent or more. When the numerator and denominator of the percentage are in different categories, use the parameter from Table 3 as indicated by the numerator.
1The approximate standard error, sy,p, of an estimated percentage can be obtained by using the formula:
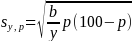 (2)
(2)
1Here y is the total number of people, families, households, or unrelated individuals in the base or denominator of the percentage, p is the percentage 100*x/y (0 ≤ p ≤ 100), and b is the parameter in Table 3 associated with the characteristic in the numerator of the percentage.
1Illustration 2
Suppose of 7,515,000 displaced workers, 2,362,000, or 31.4 percent, lost their jobs when a plant or company closed down or moved. Use the appropriate parameter from Table 3 and Formula (2) to get
Illustration 2 |
|
Percentage of displaced workers who lost their jobs when a plant or company closed down or moved (p) |
31.4 |
Base (y) |
7,515,000 |
b parameter (b) |
3,244 |
Standard error |
0.96 |
90-percent confidence interval |
29.8 to 33.0 |
1The standard error is calculated as
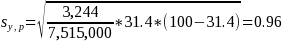

1The 90-percent confidence interval for the estimated percentage of displaced workers who lost their jobs when a plant or company closed down or moved is from 29.8 to 33.0 percent (i.e., 31.4 ± 1.645 × 0.96).
1Standard Errors of Estimated Differences. The standard error of the difference between two sample estimates is approximately equal to
 (3)
(3)
where sx1 and sx2 are the standard errors of the estimates, x1 and x2. The estimates can be numbers, percentages, ratios, etc. This will result in accurate estimates of the standard error of the same characteristic in two different areas, or for the difference between separate and uncorrelated characteristics in the same area. However, if there is a high positive (negative) correlation between the two characteristics, the formula will overestimate (underestimate) the true standard error.
1Illustration 3
Suppose that of the 8,943,000 employed men between 25-29 years of age, 1,008,000, or 11.3 percent were part‑time workers, and of the 7,920,000 employed women between 25-29 years of age, 1,714,000, or 10.3 percent were part-time workers. Use the appropriate parameters from Table 3 and Formulas (2) and (3) to get
Illustration 3 |
|||
|
Male (x1) |
Female (x2) |
Difference |
Percentage working part‑time (p) |
11.3 |
21.6 |
10.3 |
Base (y) |
8,943,000 |
7,920,000 |
- |
b parameter (b) |
2,947 |
2,788 |
- |
Standard error |
0.57 |
0.77 |
0.96 |
90-percent confidence interval |
10.4 to 12.2 |
20.3 to 22.9 |
8.7 to 11.9 |
The standard error of the difference is calculated as
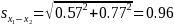
1The 90-percent confidence interval around the difference is calculated as 10.3 ± 1.645 × 0.96. Since this interval does not include zero, we can conclude with 90 percent confidence that the percentage of part-time women workers between 25-29 years of age is greater than the percentage of part-time men workers between 25-29 years of age.
Standard Errors of Estimated Medians. The sampling variability of an estimated median depends on the form of the distribution and the size of the base. One can approximate the reliability of an estimated median by determining a confidence interval about it. (See “Standard Errors and Their Use” for a general discussion of confidence intervals.)
Estimate the 68-percent confidence limits of a median based on sample data using the following procedure:
1. Determine, using Formula (2), the standard error of the estimate of 50 percent from the distribution.
2. Add to and subtract from 50 percent the standard error determined in step 1. These two numbers are the percentage limits corresponding to the 68-percent confidence interval about the estimated median.
3. Using the distribution of the characteristic, determine upper and lower limits of the
68-percent confidence interval by calculating values corresponding to the two points established in step 2.
Note: The percentage limits found in step 2 may or may not fall in the same characteristic distribution interval.
Use the following formula to calculate the upper and lower limits:
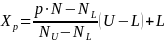 (4)
(4)
where
Xp = estimated upper and lower limits for the confidence interval
(0 ≤ p ≤ 1). For purposes of calculating the confidence interval, p takes on the values determined in step 2. Note that Xp estimates the median when p = 0.50.
N = for distribution of totals and means: the total number of units (people, households, etc.) for the characteristic in the distribution.
= for distribution of percentages: the value 100.
p = the values obtained in Step 2.
L, U = the lower and upper boundaries, respectively, of the interval containing Xp.
Note: For continuous data, i.e., income, time, etc., the upper bound of the interval containing Xp and lower bound of the next interval are essentially the same and will be treated as such in the illustration.
NL, NU = for distribution of totals and means: the estimated number of units
(people, households, etc.) with values of the characteristic less than L and U, respectively.
= for distribution of percentages: the estimated percentage of units (people, households, etc.) having values of the characteristic less than L and U, respectively.
4. Divide the difference between the two points determined in step 3 by 2 to obtain the standard error of the median.
Note: Medians and their standard errors calculated as below may differ from those in published tables and reports showing medians, since narrower income intervals were used in those calculations.
Illustration 4
Suppose you want to calculate the standard error of the estimated median of years a person worked on their lost job for all displaced workers with the following distribution:
Illustration 4 |
|||
Years on lost job |
Number of persons |
Cumulative number of persons |
Cumulative percentage of persons |
<1 |
1,660,000 |
1,660,000 |
23.60 |
1-4.99 |
3,120,000 |
4,780,000 |
67.96 |
5-9.99 |
953,000 |
5,733,000 |
81.50 |
10-14.99 |
511,000 |
6,244,000 |
88.77 |
15-19.99 |
367,000 |
6,611,000 |
93.99 |
20+ |
423,000 |
7,034,000 |
100.00 |
Total |
7,034,000 |
|
|
1. Using Formula (2) with b = 3,244 from Table 3, the standard error of 50 percent with a base of 7,034,000 is 1.07 percent.
2. To obtain a 68-percent confidence interval on an estimated median, add to and subtract from 50 percent the standard error found in step 1. This yields percentage limits of 48.24 and 51.76.
3. The lower and upper boundaries for the interval in which the percentage limits fall are L = 1 year to U = 5 years, respectively.
Then the estimated number of displaced workers with years on the lost job between 1 and 5 are NL = 1,660,000 and NU = 4,780,000, respectively.
Using Formula (4), the lower limit for the confidence interval of the median is found to be about

Similarly, the upper limit is found to be about
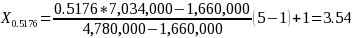
Thus, a 68-percent confidence interval for the median number of years on the lost job for displaced workers is from 3.22 to 3.54.
4. The standard error of the median is, therefore,
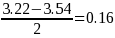
Standard Errors of Quarterly or Yearly Averages. For information on calculating standard errors for labor force data from the CPS which involve quarterly or yearly averages, please see the “Explanatory Notes and Estimates of Error: Household Data” section in Employment and Earnings, a monthly report published by the U.S. Bureau of Labor Statistics.
Technical Assistance. If you require assistance or additional information, please contact the Demographic Statistical Methods Division via e-mail at [email protected].
11Table 3. Parameters for Computation of Standard Errors for Labor Force Characteristics: January 2016 |
||
Characteristic |
a |
b |
|
|
|
Total or White |
|
|
Civilian labor force, employed |
-0.000013 |
2,481 |
Unemployed |
-0.000017 |
3,244 |
Not in labor force |
-0.000013 |
2,432 |
|
|
|
Civilian labor force, employed, not in labor force, and unemployed |
|
|
Men |
-0.000031 |
2,947 |
Women |
-0.000028 |
2,788 |
Both sexes, 16 to 19 years |
-0.000261 |
3,244 |
|
|
|
Black |
|
|
Civilian labor force, employed, not in labor force, and unemployed |
|
|
Total |
-0.000117 |
3,601 |
Men |
-0.000249 |
3,465 |
Women |
-0.000191 |
3,191 |
Both sexes, 16 to 19 years |
-0.001425 |
3,601 |
|
|
|
Asian, American Indian and Alaska Native, Native Hawaiian and Other Pacific Islander |
|
|
Civilian labor force, employed, not in labor force, and unemployed |
|
|
Total |
-0.000245 |
3,311 |
Men |
-0.000537 |
3,397 |
Women |
-0.000399 |
2,874 |
Both sexes, 16 to 19 years |
-0.004078 |
3,311 |
|
|
|
Hispanic, may be of any race |
|
|
Civilian labor force, employed, not in labor force, and unemployed |
|
|
Total |
-0.000087 |
3,316 |
Men |
-0.000172 |
3,276 |
Women |
-0.000158 |
3,001 |
Both sexes, 16 to 19 years |
-0.000909 |
3,316 |
|
|
|
Notes: (1) These parameters are to be applied to basic CPS monthly labor force estimates.
The Total or White, Black, and Asian, AIAN, NHOPI parameters are to be used for both alone and in combination race group estimates.
For nonmetropolitan characteristics, multiply the a and b parameters by 1.5. If the characteristic of interest is total state population, not subtotaled by race or ethnicity, the a and b parameters are zero.
For foreign-born and noncitizen characteristics for Total and White, the a and b parameters should be multiplied by 1.3. No adjustment is necessary for foreign-born and noncitizen characteristics for Black, Hispanic, and Asian, AIAN, NHOPI parameters.
For the groups self-classified as having two or more races, use the Asian, AIAN, NHOPI parameters for all employment characteristics.
REFERENCES
[1] Bureau of Labor Statistics, April 2014, “Redesign of the Sample for the Current Population Survey.” http://www.bls.gov/cps/sample_redesign_2014.pdf
[2] U.S. Census Bureau. 2006. Current Population Survey: Design and Methodology. Technical Paper 66. Washington, DC: Government Printing Office. (http://www.census.gov/prod/2006pubs/tp-66.pdf)
[3] Brooks, C.A. and Bailar, B.A. 1978. Statistical Policy Working Paper 3 - An Error
Profile: Employment as Measured by the Current Population Survey. Subcommittee on
Nonsampling Errors, Federal Committee on Statistical Methodology, U.S. Department of
Commerce, Washington, DC. (http://www.fcsm.gov/working-papers/spp.html)
1 For detailed information on the 2000 sample redesign, please see reference [1].
2 The PSUs correspond to substate areas (i.e., counties or groups of counties) that are geographically contiguous.
3 For further information on CATI and CAPI and the eligibility criteria, please see reference [2].
4 The phase-in process using the 2010 Census files began April 2014.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | herbs002 |
| File Modified | 0000-00-00 |
| File Created | 2021-01-22 |
© 2026 OMB.report | Privacy Policy