2019 NSCG Methodological Experiments - Minimum Detectible Differences
Appendix_J_MinDetectibleDifferences_20Oct18.docx
2017 National Survey of College Graduates (NSCG)
2019 NSCG Methodological Experiments - Minimum Detectible Differences
OMB: 3145-0141
APPENDIX J
2019 NSCG Methodological Experiments – Minimum Detectible Differences
Minimum Detectable Differences for the
2019 NSCG Methodological Experiments
Background
This appendix provides minimum detectable differences for the proposed sample sizes in each of the 2019 NSCG methodological experiments.
Adaptive Design Experiment:
New sample treatment group – 8,000 cases
Returning sample treatment group – 10,000 cases
Mailout Strategy Experiment:
New sample treatment group – 20,626 cases (approximately 6,875 per group)
Returning sample treatment group – 18,875 cases (approximately 6,292 per group)
Minimum Detectable Differences Equation and Definitions
To calculate the minimum detectable difference between two response rates with fixed sample sizes, we used the formula from Snedecor and Cochran (1989) for determining the sample size when comparing two proportions.
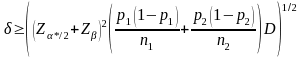
where:
= minimum detectible difference
* = alpha level adjusted for multiple comparisons
Z*/2 = critical value for set alpha level assuming a two-sided test
Z = critical value for set beta level
p1 = proportion for group 1
p2 = proportion for group 2
D = design effect due to unequal weighting
n1 = sample size for a single treatment group or control
n2 = sample size for a second treatment group or control
The alpha level of 0.10 was used in the calculations. The beta level was included in the formula to inflate the sample size to decrease the probability of committing a type II error. The beta level was set to 0.10.
The estimated proportion for the groups was set to 0.50 for the sample size calculations. This conservative approach minimizes the ability to detect statistically significant differences.
Design effects represent a variance inflation factor due to sample design when compared to a simple random sample. Because all experiment samples and the control will be representative, the weight distributions should be similar throughout all samples, negating the need to include a design effect. We do not expect to see a weight-based or sampling-based effect on response in any of the samples. However, for the sake of completeness, minimum detectible differences were calculated both ways, including and ignoring the design effect.1
Pairwise Comparisons and the Bonferroni Adjustment
The number of pairwise comparisons included in the adaptive design experiment evaluation is one (treatment vs. control). For the contact strategies experiment, the number of pairwise comparisons increases because numerous treatment groups can be compared as discussed in the research questions listed in Appendix I. In these instances, * is adjusted to account for the multiple comparisons.
The Bonferroni adjustment reduces the overall by the number of pairwise comparisons so when multiple pairwise comparisons are conducted the overall will not suffer. The formula is:
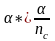
The adjusted alpha * is calculated by dividing the overall target by the number of pairwise comparisons, nc. It is worth noting that, despite being commonly used, the Bonferroni adjustment is very conservative, actually reducing the overall below initial targets. An example showing how the overall is calculated using an alpha level of 0.10, the Bonferroni adjustment, and 11 pairwise comparisons follows:
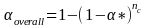
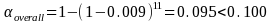
overall is the resulting overall after the Bonferroni correction is applied;
target = 0.100, and is the original target level;
nc = 11, and is the number of comparisons (i.e., Appendix I research questions)
* = overall/ nc = 0.009, and is the Bonferroni-adjusted
In this example, the Bonferroni adjustment actually overcompensates for multiple comparisons, making it more likely that a truly significant effect will be overlooked.
Sample sizes were provided by NCSES in section I of this appendix and are used in the formula. All minimum detectable differences using the Bonferroni adjustment were calculated and are summarized at the end of this appendix in table form.
A Model-Based Alternative to Multiple Comparisons
Rather than relying on the Bonferroni adjustment for multiple comparisons, effects on response, cost per case or other outcome variables could be modeled simultaneously to determine which treatments have a significant effect on response.
All sample cases, auxiliary sample data, and treatments are included in the model below, which predicts a given treatment’s effect on response rate (or other outcome variable).
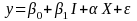
Assuming response rate is the outcome variable of interest:
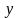 is the average response
propensity (response rate) for the entire sample;
is the average response
propensity (response rate) for the entire sample;
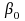 is the intercept for the model;
is the intercept for the model;
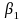 is a vector of effects, one for
each treatment;
is a vector of effects, one for
each treatment;
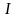 is a vector of indicators to
identify a treatment in
is a vector of indicators to
identify a treatment in
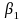 ;
;
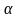 is a scalar vector;
is a scalar vector;
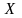 is a matrix of auxiliary frame or
sample data; and
is a matrix of auxiliary frame or
sample data; and
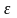 is an error term.
is an error term.
Once data collection is complete, the average response propensity is equal to the response rate. In the simplest case, no treatment has any effect (the 2nd term would drop out), and no auxiliary variables explain any of the variation in response propensities (the 3rd term would drop out). In that case, the average of the response propensities, and thus the response rate, would just equal:
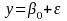
However, a more complicated model gives information about each treatment’s effect (2nd term) while taking into account sample characteristics (3rd term) that might augment or reduce the effect of a given treatment.
As a simple example, ignore the error term, and assume the overall mean response propensity was 72%. Also, assume the mean response propensity for a given treatment group was 83%. If only terms 1 and 2 were included in the model (no sample characteristics accounted for), the given treatment appears to have increased the response propensity by 11%. However, if the sample was poorly designed, or if a variable not included in the sample design turned out to be a good predictor of response, there is value in adding the 3rd term. If auxiliary information added by the 3rd term shows that the cases in a particular sample group are 5% more likely to respond than the average sample case (because of income, internet penetration, age, etc.), this would suggest that while the treatment group had a response propensity 11% higher than the average, 5% came from sample person characteristics, and only 6% of that increase was really due to the treatment.
This method has several benefits
over the multiple comparisons method. First, the number of degrees
of freedom taken up by the model is the number of treatment groups
plus one for the intercept, which is fewer than the number of
pairwise comparisons that might be conducted. Second, because
confidence intervals are calculated around the
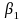 values, it is easier to observe a treatment’s effect on the
outcome measures. Third, variables can be controlled for in the
model, making significant results more meaningful. While we are
striving to ensure the experimental samples are as representative
(and as similar) as possible, the ability to add other variables to
the model helps control for unintended effects.
values, it is easier to observe a treatment’s effect on the
outcome measures. Third, variables can be controlled for in the
model, making significant results more meaningful. While we are
striving to ensure the experimental samples are as representative
(and as similar) as possible, the ability to add other variables to
the model helps control for unintended effects.
The method uses response
propensities, not the actual response rate. While the mean response
propensity after the last day of data collection equals the overall
response rate, it is important to note how the propensity models are
built. If they are weighted models, weighted response propensities
should be used in this model. The weights could be added as one of
the auxiliary variables included in the
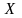 matrix.
matrix.
Comments
It is worth noting from the calculations below that even using the Bonferroni adjustment, and conducting all pairwise comparisons, a difference of 6% - 8% in outcome measures should be large enough to appear significant, when the design effect is excluded from the calculations. Because the experimental samples are all systematic random samples, and should have similar sample characteristics and weight distributions, excluding the design effect seems appropriate.
Minimum Detectable Differences for the 2019 NSCG Methodological Experiments |
|
|
||||||||||||||||||||
|
||||||||||||||||||||||
M |
|
|
= |
minimum detectible difference |
||||||||||||||||||
|
|
|
|
|
= |
minimum detectible difference without using design effect |
||||||||||||||||
|
|
|
* |
= |
alpha level adjusted for multiple comparisons (Bonferroni) |
|||||||||||||||||
|
|
|
Z*/2 |
= |
critical value for set alpha level assuming a two-sided test |
|||||||||||||||||
|
|
|
|
Z |
= |
critical value for set beta level |
||||||||||||||||
|
|
|
|
p1 |
= |
proportion for group 1 |
||||||||||||||||
|
|
|
|
p2 |
= |
proportion for group 2 |
||||||||||||||||
|
|
|
|
deff |
= |
design effect due to unequal weighting |
||||||||||||||||
|
|
|
|
n1 |
= |
sample size for group 1 |
||||||||||||||||
|
|
|
|
n2 |
= |
sample size for group 2 |
||||||||||||||||
|
|
|||||||||||||||||||||
Adaptive Design Experiment (new sample) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
8,000 Cases in Experimental Group |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
* |
= |
0.100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z*/2 |
= |
1.645 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
= |
1.282 |
|
0.0568 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 |
= |
0.5 |
|
0.0231 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
= |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
deff |
= |
6.02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
= |
8,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
= |
30,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Adaptive Design Experiment (returning sample) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
10,000 Cases in Experimental Group |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
* |
= |
0.100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z*/2 |
= |
1.645 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
= |
1.282 |
|
0.0460 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 |
= |
0.5 |
|
0.0207 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
= |
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
deff |
= |
4.95 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
= |
10,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
= |
49,000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mailout Strategy Experiment (new sample)
20,626 cases in Experimental Group; 3 treatment groups
* |
= |
0.033 |
|
|
Z2 |
= |
2.128 |
|
|
Z |
= |
1.282 |
|
0.0564 |
p1 |
= |
0.5 |
|
0.0230 |
p2 |
= |
0.5 |
|
|
deff |
= |
6.02 |
|
|
n1 |
= |
6,875 |
|
|
n2 |
= |
27,724 |
|
|
Mailout Strategy Experiment (returning sample)
18,875 cases in Experimental Group; 3 treatment groups
* |
= |
0.033 |
|
|
Z*/2 |
= |
2.128 |
|
|
Z |
= |
1.282 |
|
0.0526 |
p1 |
= |
0.5 |
|
0.0236 |
p2 |
= |
0.5 |
|
|
deff |
= |
4.95 |
|
|
n1 |
= |
6,292 |
|
|
n2 |
= |
30,315 |
|
|
1 Design effects were calculated by examining the weight variation present in all cases in the 2017 NSCG new sample (6.02), and the returning sample (4.95).
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Milan, Lynn M. |
| File Modified | 0000-00-00 |
| File Created | 2021-01-20 |
© 2026 OMB.report | Privacy Policy
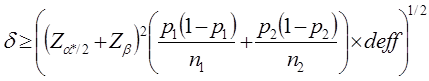 inimum
Detectable Difference Equation for Response Rates
inimum
Detectable Difference Equation for Response Rates