Methods Used to Calculate the Variances of the OSHS Case and Demographic Estimates
Variance Estimation for SOII Case and Demographic Estimates 2-22-02.docx
Survey of Occupational Injuries and Illnesses
Methods Used to Calculate the Variances of the OSHS Case and Demographic Estimates
OMB: 1220-0045
METHODS USED TO CALCULATE THE VARIANCES OF THE OSHS CASE AND DEMOGRAPHIC ESTIMATES
FEBRUARY 22, 2002
INTRODUCTION
In an effort to reduce the computer time required to calculate the variances for the Case and Demographic estimates, we decided that the variances would be computed using models. The equations presented here may seem to be surprisingly simple given the complexity of the survey, but we are confident that the statistical basis for the use of these equations is strong.
This paper derives variance and relative standard error equations for the three types of Case and Demographic estimates:
PROPORTION
TOTAL
RATIO
The paper also gives an example of the calculations for each of these types.
When applying these equations, it is important to use the appropriate DAFW case sample size. If, within an area, the estimates are for All Industries, the sample size is the total number of unweighted sample DAFW cases for the area. If the estimate is restricted to a particular industry within the area, the sample size is the number of unweighted sample DAFW cases for that industry within the area.
PROPORTION
In this type of estimator, for an area, we are estimating the proportion, phi hat, of the total number of DAFW cases in industry i that have characteristic h. Under the assumption that the design effect is one and that the total DAFW case sample size for the industry is fixed, we can use the standard variance formula for simple random sampling without replacement to model the variances and relative standard errors for these proportions:
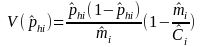
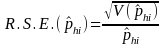
where for the area
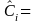 estimate
of the total number of DAFW cases for industry i
estimate
of the total number of DAFW cases for industry i
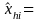 total
number of weighted sample DAFW cases with characteristic h for
industry i
total
number of weighted sample DAFW cases with characteristic h for
industry i
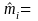 total
number of unweighted sample DAFW cases for industry i
total
number of unweighted sample DAFW cases for industry i
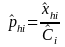
TOTAL
In this type of estimator, for an area, we are estimating the number of DAFW cases , Ehi hat, in industry i that have characteristic h. Investigation into the micro data file led us to have a high degree of confidence that the estimates of the total number of cases for a particular group (such as SIC 17) and the proportion of the cases in the group with a particular characteristic (such as male) are statistically independent. This simplifies the variance calculation; for, if two random variables are independent, the variance of their product can be expressed in the following way (Quality Control and Industrial Statistics, Duncan, p. 104)
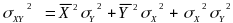
A further simplification of the variance calculation is possible because the design effect for a Case and Demographic estimate of proportion is approximately one. This means that, for estimating proportions, the stratified sample of DAFW cases is statistically equivalent to a sample random sample of cases with the same sample size.
Since: 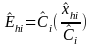 and since
and since
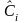 and
and
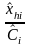 are
statistically independent:
are
statistically independent:
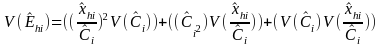
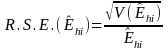
where for the area
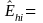 estimate
of the total number of DAFW cases with characteristic h for industry
i
estimate
of the total number of DAFW cases with characteristic h for industry
i
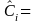 estimate
of the total number of DAFW cases for industry i
estimate
of the total number of DAFW cases for industry i
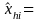 total
number of weighted sample DAFW cases with characteristic h for
industry i
total
number of weighted sample DAFW cases with characteristic h for
industry i
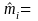 total
number of unweighted sample DAFW cases for industry i
total
number of unweighted sample DAFW cases for industry i
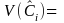 variance
for the estimated number of DAFW cases in industry i
variance
for the estimated number of DAFW cases in industry i
This value comes from the summary estimates.
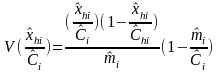
= variance of the proportion of the cases with characteristic h for industry i
RATIO
In this type of estimator, for industry i in an area, we are estimating the ratio, Rhki hat, of the total number of DAFW cases that have characteristic h to the number of cases that that have both characteristic h and characteristic k. For example, the proportion of the total number of DAFW cases in an industry that are male that fall within a certain range of number of days lost. We can express this ratio of two totals as the quotient of two statistically independent proportions:
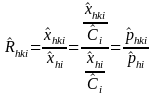
From Quality Control and Industrial Statistics, Duncan, p. 104, the following variance formula is a valid approximation for the ratio.
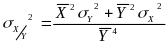
Therefore
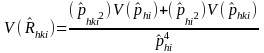
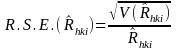
where for the area
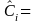 estimate
of the total number of DAFW cases for industry i
estimate
of the total number of DAFW cases for industry i
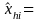 total
number of weighted sample DAFW cases with characteristic h for
industry i
total
number of weighted sample DAFW cases with characteristic h for
industry i
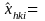 total
number of weighted sample DAFW cases with characteristics h and k for
industry i
total
number of weighted sample DAFW cases with characteristics h and k for
industry i
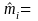 total
number of unweighted sample DAFW cases for industry i
total
number of unweighted sample DAFW cases for industry i
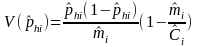
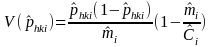
NUMERICAL EXAMPLE 1: PROPORTION
Here we are estimating the proportion of Delaware DAFW cases in SIC 17 that occurred to males. In this example industry i is SIC 17 and characteristic h is male.
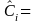 estimated number of Delaware DAFW cases in SIC 17 = 318
estimated number of Delaware DAFW cases in SIC 17 = 318
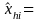 total number of weighted Delaware DAFW cases in SIC 17 that occurred
to males = 299
total number of weighted Delaware DAFW cases in SIC 17 that occurred
to males = 299
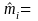 total
number of unweighted Delaware DAFW cases in SIC 17 = 189
total
number of unweighted Delaware DAFW cases in SIC 17 = 189
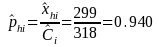
Therefore:
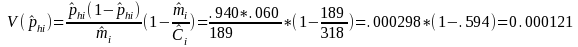
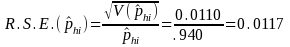
NUMERICAL EXAMPLE 2: TOTAL
We are estimating the total number of Delaware DAFW cases that occurred to males; therefore, industry i is All Industries and characteristic h is male
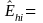 estimate
of the total number of Delaware DAFW cases for males in All
Industries = 3237
estimate
of the total number of Delaware DAFW cases for males in All
Industries = 3237
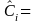 estimate
of the total number of Delaware DAFW cases in All Industries = 5128
estimate
of the total number of Delaware DAFW cases in All Industries = 5128
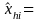 total number of weighted
sample Delaware DAFW cases for males in All Industries = 3237
total number of weighted
sample Delaware DAFW cases for males in All Industries = 3237
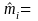 total number of unweighted
Delaware DAFW cases for All Industries = 2497
total number of unweighted
Delaware DAFW cases for All Industries = 2497
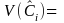 variance
for the estimated number of Delaware DAFW cases in All Industries =
12472
variance
for the estimated number of Delaware DAFW cases in All Industries =
12472
This value comes from the summary estimates.
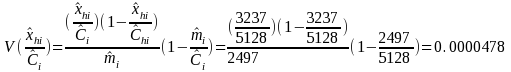
Therefore:
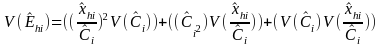
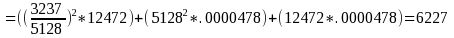
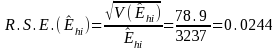
NUMERICAL EXAMPLE 3: RATIO
We are estimating the ratio of the number of Delaware DAFW cases that occurred to males that had 1 to 5 days away from work to the number of DAFW cases that occurred to males. In this example, industry i is All Industries, characteristic h is male, and characteristic k is 1 to 5 days away from work.
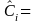 estimate
of the total number of Delaware DAFW cases for All Industries = 5128
estimate
of the total number of Delaware DAFW cases for All Industries = 5128
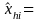 total
number of weighted sample Delaware DAFW cases for males in All
Industries = 3237
total
number of weighted sample Delaware DAFW cases for males in All
Industries = 3237
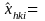 total
number of weighted sample Delaware DAFW cases for males and 1 to 5
days away from work in All Industries = 1607
total
number of weighted sample Delaware DAFW cases for males and 1 to 5
days away from work in All Industries = 1607
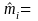 total
number of unweighted sample Delaware DAFW cases for All Industries =
2497
total
number of unweighted sample Delaware DAFW cases for All Industries =
2497
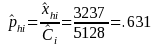
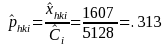
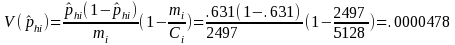
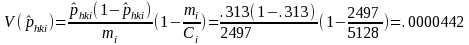
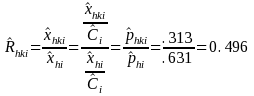
Therefore:
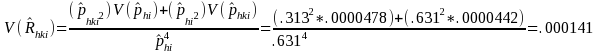
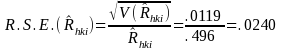
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | DRAFT |
| Author | John Kelley |
| File Modified | 0000-00-00 |
| File Created | 2022-08-01 |
© 2026 OMB.report | Privacy Policy