Diagnostic Teachers Assessments in Mathematics and Scien
Visual Representations for Proportional Reasoning: Impacts of a Teacher Professional Development Program for Multilingual Learners and Other Students
NE 5.1.1 CT DTAMS instrument
Diagnostic Teachers Assessments in Mathematics and Science (DTAMS, Number/ Computation Form)
OMB: 1850-0978
According to the Paperwork Reduction Act of 1995, no persons are required to respond to a collection of information unless such collection displays a valid OMB control number. The valid OMB control number for this information collection is 1850-xxxx. Public reporting burden for this collection of information is estimated to average 1 hour per response, including time for reviewing instructions, searching existing data sources, gathering and maintaining the data needed, and completing and reviewing the collection of information. The obligation to respond to this collection is voluntary. If you have any comments concerning the accuracy of the time estimate, suggestions for improving this individual collection, or if you have comments or concerns regarding the status of your individual form, application or survey, please contact Janelle Sands at the Institute of Education Sciences (IES) at [email protected] directly.
Thank you for participating in the Regional Educational Laboratory Northeast and Islands’ evaluation of the Visual Access to Mathematics Professional Development (“VAM PD”) program. The following set of questions is expected to take 1 hour to complete.
DTAMS Number/Computation Form 1 (pre-test)
1. [Multiple Choice] Rachel and Selena live 24 miles apart along a bike trail. Last Saturday each left her own house at 10 AM and rode her bike along the trail towards the other. They met at noon. Rachel rode her bike at a rate of 6.5 miles per hour (mph).
How fast did Selena ride?
12 mph
11 mph
8.75 mph
5.5 mph
2. [Multiple Choice] The average price of a computer decreased by one third between 1990 and 2000.
If the average price of a computer in 2000 was $1260, what was the average price in 1990?
$840
$1890
$2520
$3780
3. [Multiple Choice] Mario is using his grandmother’s recipe to make lemonade for the school festival. He knows that the amount of lemon juice he needs is proportional to the amount of water.
Which equation could show the relationship between the amount of lemon juice, j , and the amount of water, w, in the recipe?
j = 5/w
j = w/5
j = 5w
j = w5
4. [Multiple Choice] Trey can drive his battery powered jeep 1.6 kilometers in 45 minutes. Approximately how many hours would it take him to drive 30 km at the same constant speed?
14 hours
15 hours
18 hours
28 hours
5. [Multiple Choice] When a square is enlarged such that its new perimeter is five times its original perimeter, what is the ratio of the square's original area to its new area?
25 : 1
1 : 25
5 : 1
1 : 5
6. [Multiple Choice] A 1% saline solution is composed of 99% water and 1% salt. A 1 quart bottle of 1% saline solution is mixed with a 1 gallon jug (4 quarts) of 4% saline solution.
What is the percentage of salt in the final mixed solution?
2.5%
3.5%
5.8%
8.6%
7. [Text Box] Fred, Nick, and Tara are paid $20 to seal envelopes. They agree to divide it in the same proportion as the number of envelopes they seal. Fred sealed 63 envelopes. Nick sealed 27 more than Tara and Nick received $8 of the $20.
In terms of n = number of envelopes sealed by Nick, set up the following:
A. [Open Response] An expression for Tara's share of the $20 payment.
B. [Open Response] An equation whose solution gives the value of n.
8. Best Ever Bakery uses five recipes to make orange icing to decorate birthday cakes, as shown in the following table. The chart below shows the shades of icing created by mixing red and yellow icing.
|
Recipe A |
Recipe B |
Recipe C |
Recipe D |
Recipe E |
YELLOW |
1 part |
2 parts |
4 parts |
2 parts |
4 parts |
RED |
3 parts |
5 parts |
12 parts |
6 parts |
10 parts |
a. [Open Response] How many different shades of icing did the bakery make?
b. [Open Response] Which recipe(s) have a greatest proportion of red? Explain your answer.
c. [Open Response] Write an equation that relates y, the number of parts of yellow icing, and r, the number of parts of red icing for each of the shades of icing.
9. [Order] Order the following set of numbers from least to greatest.
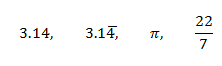
10. [Open Response] Does a < b imply that 1/a > 1/b for all nonzero a and b? If so, give a proof; if not, give a counterexample.
11. [Multiple Choice] Which of these statements is TRUE?
Some whole numbers are irrational numbers.
Some irrational numbers are not real numbers.
Some integers are not rational numbers.
Some rational numbers are nonterminating decimal numbers.
12. [Multiple Choice] Find the value of the expression. 10 • 22 • 30 • 42
64
32
16
0
13. [Multiple Choice] Which law justifies the equality:
(2 × 6) + (3 + 4) = (3 + 4) + (2 × 6)
associative law of multiplication
commutative law of addition
commutative law of multiplication
associative law of addition
14. [Open Response] Jars A and B contain five numbered chips. The chips in Jar A have the values –8, 5, 4, –7, and 6. The chips in Jar B have the values –7, 6, –9, –8, and 7. One chip is drawn from each jar and the product of their values is computed.
Using your knowledge of integer operations, explain how to find the two chips with the smallest product.
15. [Multiple Choice] Which point on the number line below (A, B, C, or D) most accurately represents 5/4?

Point A
Point B
Point C
Point D
16. [Multiple Choice] Which problem can be solved by multiplying ⅓ and ¼?
There is one third of a pie remaining. Jinx eats one fourth of the leftover pie. How much pie is left?
Max eats one third of a pie. Jinx eats one fourth of the leftover pie. How much pie is left?
Max eats two thirds of a pie. Jinx eats one fourth of the leftover pie. How much of the pie did Jinx eat?
Max eats one third of a pie. Jinx eats one fourth of the leftover pie. How much of the pie did Jinx eat?
17.
[Multiple
Choice] Ralph has 2
![]() cups of flour and needs 4
cups of flour and needs 4
![]() cups of flour to make one loaf of bread. How many loaves can he make?
cups of flour to make one loaf of bread. How many loaves can he make?
4/7 loaves
2 loaves
½ loaves
7/4 loaves
18. [Open Response] Consider a student’s response to the following problem:
Problem:
A boy and a girl run equally fast around a track. The boy started first and had run 8 laps when the girl had run 2 laps. When the girl had run 12 laps, how many laps had the boy run?
Student’s response:
“This problem is easy. You just set up a proportion and solve it like this.
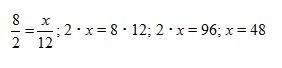
That means the boy had run 48 laps when the girl had run 12, just like he had run 8 laps when she had run 2.”
Is the solution strategy given by the student correct or incorrect? Explain your response in terms of proportional and additive thinking.
19. [Multiple Choice] This example of a student’s work on proportional reasoning most likely shows a difficulty in which area?
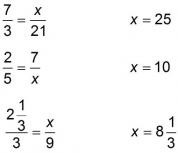
Multiplicative comparison
Absolute reasoning
Unit rate
Equivalence property
20. [Multiple Choice] Paper towels of standard width come in cylindrical rolls. The radius of the jumbo size roll is twice that of the regular size roll.
Which student uses the most accurate reasoning in comparing the number of sheets needed to decrease each roll to half of its initial radius?
Abe says: Based on equal volume sheets, the jumbo roll needs about 23 = 8 times as many.
Bob says: Based on equal width sheets, the jumbo roll needs about 22 = 4 times as many.
Cal says: Based on equal area sheets, the jumbo roll needs about 21 = 2 times as many.
Dan says: Based on the same fractional decrease, both rolls need about equally as many.
21. [Open Response] Describe how you would use a set or area model to demonstrate why the ratio 3 : 5 : 9 is equivalent to 6 : 10 : 18. Be sure to label or clearly explain your model.
22. [Open Response] The teacher provides this Venn Diagram to her students and poses the following problem:
If this Venn Diagram represents rational numbers (r) such that r > 1/2 , r < 1 , and r has a denominator of 10, determine if regions label A, B, C, and D are infinite, finite, or empty.
Students quickly respond the four regions are all finite. In the diagram below, assume x is an integer.
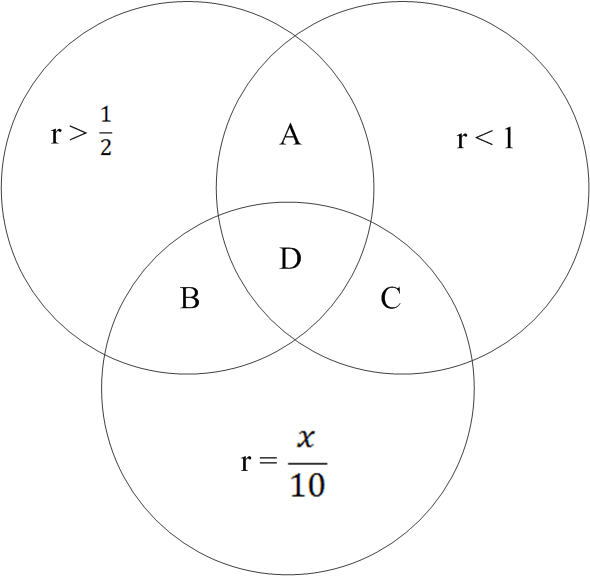
Determine if students' initial responses are correct; then help the students to justify or refine their response with accurate mathematical reasoning.
DTAMS Number/Computation Form 2 (post-test)
1. Raven and Jamie are in two different algebra classes and are comparing their grades after four tests. Jamie is in Mr. Brown’s class. Mr. Brown's tests vary in the number of points. Raven is in Ms. Green's class. Ms. Green's tests are all worth 100 points. Raven averages her scores and gets 87% over the four tests. Jamie averages his scores and gets 88%.
-
Test 1
Test 2
Test 3
Test 4
Mr. Brown’s tests
50
90
50
90
Jamie’s scores
94%
80%
96%
83%
Ms. Green’s tests
100
100
100
100
Raven's scores
90%
80%
92%
85%
[Multiple Choice] Which statement is correct?
Jamie’s procedure will work for both him and Raven.
Jamie’s procedure will NOT work for either him or Raven.
Jamie’s procedure will work for him but NOT for Raven.
Jamie’s procedure will NOT work for him but will work for Raven.
2. [Multiple Choice] If the price of a can of soda is raised from 80 cents to 90 cents, what is the percent increase in the price?
10.0%
11.1%
12.5%
88.8%
3. [Multiple Choice] A two cup mixture consists of 3/4 cup of sugar and the rest is flour. If one cup of sugar is added to make a three cup mixture, what is the ratio of sugar to flour in the three cup mixture?
5 : 7
7 : 5
5 : 12
7 : 12
4. [Open Response] The high school championship game begins in one hour. You are in line to get your ticket behind 187 people. You determine that 8 people can purchase tickets in 100 seconds. With your purchase of a ticket, how much time, to the nearest minute, will remain to get popcorn and find your seat?
5. Brianna and Reba are twin sisters. They each received a birthday gift from their grandmother for the same amount of money. Brianna bought a book for $25 and Reba bought a graphing calculator for $100. After their purchases, the ratio of Brianna’s money to Reba’s money was 5:2.
[Multiple Choice] Which equation can be used to determine the amount of money each sister received for her birthday gift?
5x – 2x = 75
5x + 2x = 125
2(x – 100) = 5(x – 25)
5(x – 100) = 2(x – 25)
6. A laptop computer is discounted X percent. A week later, the discounted price is further discounted Y percent.
[Multiple Choice] If P is the original price, and X and Y represent the percentages of discount, which equation accurately represents the final selling price?
Selling Price = P • X • Y
Selling Price = P (1 – X) (1 – Y)
Selling Price = P – X – Y
Selling Price = P – X • Y
7. Best Ever Bakery uses five recipes to make orange icing to decorate birthday cakes, as shown in the following table. The chart below shows the shades of icing created by mixing red and yellow icing.
|
Recipe A |
Recipe B |
Recipe C |
Recipe D |
Recipe E |
YELLOW |
1 part |
2 parts |
4 parts |
2 parts |
4 parts |
RED |
3 parts |
5 parts |
12 parts |
6 parts |
10 parts |
a. [Open Response] How many different shades of icing did the bakery make?
b. [Open Response] Which recipe(s) have a greatest proportion of red? Explain your answer.
c. [Open Response] Write an equation that relates y, the number of parts of yellow icing, and r, the number of parts of red icing for each of the shades of icing.
8. A rectangular photo 10 cm wide is enlarged so that its area is doubled.
[Multiple Choice] How wide is the enlarged photo?
10√2
20
20√2
40
9. [Multiple Choice] If a, b, and c are real numbers, what is the distance between b – a and b + c on a number line?
|c + a|
|c – a|
|c| + |a|
|c + 2b – a|
10. [Order/Rank] Order the following set of numbers from least to greatest.
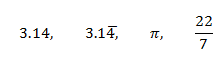
11. [Multiple Choice] Which of these statements is TRUE?
Some whole numbers are irrational numbers.
Some irrational numbers are not real numbers.
Some integers are not rational numbers.
Some rational numbers are nonterminating decimal numbers.
12. [Multiple Choice] Which statement is true when you divide –55 by a negative integer?
The quotient will be positive and less than or equal to 55.
The quotient will be negative and less than or equal to –55.
The quotient will be positive and greater than or equal to 55.
The quotient will be negative and greater than or equal to –55.
13. [Multiple Choice] Evaluate the following expression.
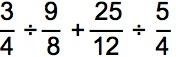
2-1/10
2-1/5
2-1/3
3-19/45
14. Jars A and B contain five numbered chips. The chips in Jar A have the values –8, 5, 4, –7, and 6. The chips in Jar B have the values –7, 6, –9, –8, and 7. One chip is drawn from each jar and the product of their values is computed.
[Open Response] Using your knowledge of integer operations, explain how to find the two chips with the smallest product.
15. [Multiple Choice] The temperature changed at a steady rate from 11° to 5° in a 12hour period. What was the rate of change per hour?
-1-1/3 degrees
-1/2 degrees
½ degrees
1-1/3 degrees
16. [Multiple Choice] Which point on the number line below (A, B, C, or D) most accurately represents 5/4?

Point A
Point B
Point C
Point D
17. [Multiple Choice] Which problem can be solved by multiplying ⅓ and ¼?
There is one third of a pie remaining. Jinx eats one fourth of the leftover pie. How much pie is left?
Max eats one third of a pie. Jinx eats one fourth of the leftover pie. How much pie is left?
Max eats two thirds of a pie. Jinx eats one fourth of the leftover pie. How much of the pie did Jinx eat?
Max eats one third of a pie. Jinx eats one fourth of the leftover pie. How much of the pie did Jinx eat?
18. You pose the following problem to your students:
In the given picture, what is the ratio of lemonade concentrate to water for the drink mix?
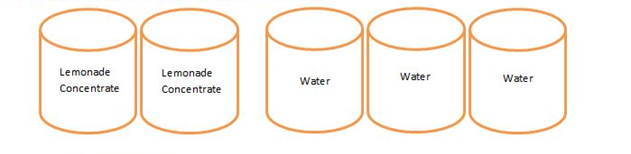
Emeril answers 2:3
Rachel answers “There is 1 can of lemonade for 3/2 can of water”
[Open Response] Emeril is clearly correct. How would you explain to him why Rachel’s answer is right or wrong?
19. Consider a student’s response to the following problem:
Problem: Jose and his friends work for a home remodeling company during the summer.
It takes 3 people 4 hours to paint a living room. If 6 people paint at the same rate,
how long will it take them to paint the same room?
Student’s response:
“This problem is easy. You just set up a proportion and solve it like this.

It will take 8 hours for 6 people to paint the living room.”
[Open Response] Is the solution strategy given by the student correct or incorrect? If incorrect, give the correct answer and describe the student's misconception.
20. Marco was given the following problem to solve.
The upstairs bathroom faucet dripped 2 oz. of water in 16 minutes while the downstairs bathroom faucet dripped 7 oz. of water in 56 minutes.
[Open Response] Marco states that the downstairs bathroom faucet drips at a faster rate than the upstairs faucet because the numbers are larger. Describe an instructional strategy that will help Marco understand if his reasoning is correct.
21. Paper towels of standard width come in cylindrical rolls. The radius of the jumbosize roll is twice that of the regularsize roll.
[Multiple Choice] Which student uses the most accurate reasoning in comparing the number of sheets needed to decrease each roll to half of its initial radius?
Abe says: Based on equalvolume sheets, the jumbo roll needs about 23 = 8 times as many.
Bob says: Based on equalwidth sheets, the jumbo roll needs about 22 = 4 times as many.
Cal says: Based on equalarea sheets, the jumbo roll needs about 21 = 2 times as many.
Dan says: Based on the same fractional decrease, both rolls need about equally as many.
22. The teacher provides this Venn Diagram to her students and poses the following problem:
If this Venn Diagram represents rational numbers (r) such that r > 1/2 , r < 1 , and r has a denominator of 10, determine if regions label A, B, C, and D are infinite, finite, or empty.
Students quickly respond the four regions are all finite. In the diagram below, assume x is an integer.

[Open Response] Determine if students' initial responses are correct; then help the students to justify or refine their response with accurate mathematical reasoning.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Modified | 0000-00-00 |
| File Created | 0000-00-00 |
© 2026 OMB.report | Privacy Policy