Personal Responsibility Education Program (PREP) Local Evaluation Support Instruments
Formative Data Collections for ACF Program Support
Instrument 2 - PREIS Analysis Plan Template (002)
Personal Responsibility Education Program (PREP) Local Evaluation Support Instruments
OMB: 0970-0531
October
2024
Template
and Guidance


PREIS
Analysis Plan
Template
and Guidance

PREIS Analysis Plan Template
Authors
Randall Juras, Michelle Blocklin, and Cristofer Price (Abt Global), with support from the PREP Local Evaluation Support team. We’d also like to acknowledge the thoughtful contributions of the PREIS Steering Committee.

Abt Global LLC | 6130 Executive Boulevard | Rockville, MD 20852


The
purpose of this information collection is to help PREIS
grantees develop data analysis plans.
Public reporting burden for this collection of information is
estimated to average 12 hours per respondent, including the time for
reviewing instructions, gathering, and maintaining the data needed,
and reviewing the collection of information. This
is a voluntary collection of information. An
agency may not conduct or sponsor, and a person is not required to
respond to, a collection of information subject to the requirements
of the Paperwork Reduction Act of 1995, unless it displays a
currently valid OMB control number. The OMB # is 0970-0531 and the
expiration date is 9/30/2025. If
you have any comments on this collection of information, please
contact Selma Caal ([email protected]).
CONTENTS
Overview of Analysis Plan Requirement ii
Template for Statistical Analysis Plan (Evaluation Plan Section 2.5) 1
2.5.2 Approach to hypothesis testing 2
2.5.3. Attrition and baseline equivalence 3
2.5.5 Differences in approach for secondary contrasts 8
2.5.8 Sensitivity analysis (optional) 10
Appendix C: Detailed specification of measures to be analyzed 12
Overview of Analysis Plan Requirement
The purpose of Personal Responsibility Education Innovative Strategies (PREIS) program evaluations is to determine the effectiveness of the innovative interventions and/or approaches on behavior change. Grantees have developed evaluation design plans specifying local impact evaluations that are rigorous in nature, meaning they use a randomized controlled trial (RCT) or a high-quality quasi-experimental design (QED). These evaluations are designed to answer both primary and secondary grantee-specific research questions.
In addition to using a well-specified rigorous design, a key element of evaluation rigor is pre-specification of the primary impact analysis methods. For that reason, PREIS programs and their local evaluators are required to develop an analysis plan in collaboration with the Family and Youth Services Bureau (FYSB). FYSB approval will be required prior to implementation of a proposed analysis plan.
This template is provided to PREIS grantees to assist in the development of their analysis plan. It includes the required components of an analysis plan as delineated in the Notice of Funding Opportunity (NOFO), as well as the expectations described in the PREIS Standards for Rigor, and provides a logical flow for describing them.
The local evaluation support (LES) team will support the grantees’ development of their analysis plans, through individual support as well as additional resources and webinars. Grantees will be expected to submit draft versions of their analysis plans or sections of their plans according to the review schedule they develop in partnership with their LES liaison. This schedule helps ensure the LES team is able to provide ongoing feedback during the plan development, with the expectation that all or almost all components of draft analysis plans will have been reviewed at least once by the LES liaison prior to the complete plan submission by March 2025.
Once evaluators send completed analysis plans to the LES team, the LES team will review the plans in coordination with FYSB. LES liaisons will support grantees and evaluators in revising analysis plans until they meet the Standards for Rigor and are approved by FYSB.
How to use this Document
The following sections present a template for your analysis plan, which should be completed by the evaluation team. These sections are intended to replace section 2.5 of your evaluation plan and are numbered correspondingly. To submit your analysis plan for review, please replace section 2.5 of your current up-to-date evaluation plan in its entirety and resubmit the evaluation plan.
Instructions are included below for completing each section of the analysis plan (i.e., the new section 2.5 of your evaluation plan). In each section, applicable Expectations from the Standards for Rigor are shown in red-outlined text boxes. Additional information (e.g., definitions, tips, explanations) is included in blue-shaded text boxes.
Expectation
1C.1:
Good scientific practice requires specifying key elements of how an
evaluation, especially the data analysis, will be conducted in
advance of observing the outcome data; it also requires some
discipline in following the analysis plan. Pre-specifying an
analysis plan gives an evaluator the opportunity to identify the
research questions that will be addressed and to describe how the
evaluator will address the research questions before collecting and
analyzing outcome data.

Template for Statistical Analysis Plan (Evaluation Plan Section 2.5)
In the subsections that follow, describe detailed plans for conducting the statistical analysis for your impact evaluation. Describe your analysis plans for your primary contrasts in Sections 2.5.1 through 2.5.4, and in Section 2.5.5 describe any differences in your analysis plans for your secondary contrasts.
Note that some of the subsections below may not be applicable for your specific study design. Please discuss with your LES liaison to confirm whether sections are not applicable and note N/A under corresponding section headers.
2.5.1 Data preparation
Outliers and inconsistencies
Describe your approach for cleaning and preparing the baseline and follow up data for analysis. Include protocols for detecting and correcting inconsistencies between outcomes within a survey wave (for example, a respondent saying they have never had sex but also that they used a condom at last intercourse) and between survey waves (for example, a respondent saying they are sexually active at the 3 month follow up but saying they have never had sex at the 12 month follow up). Describe your approach to identifying and correcting for implausible values (i.e., “outliers”) for continuous and open-ended variables (for example, a respondent identifying their age as well outside the range of program eligibility or their number of sexual partners as implausibly large).
Tip: Unless the mechanism by which an outlier occurred is unambiguous, which is rare, the LES team recommends treating implausible outliers as missing data. (Outliers that could be confidently corrected would be, for example, if a youth in a program serving mostly 14 and 15 year olds entered their age as 115 or 155 instead of 15; or a youth in a program serving 8th and 9th graders entered their grade level as 88 instead of 8). |
Missing data
Describe your approach for dealing with:
Missing outcome data (preferably using a method endorsed by the What Works Clearinghouse; e.g., case deletion, weighting, or imputation).

Expectation 2A.1.g: Evaluation must use acceptable practices for addressing missing data. To satisfy this criterion, evaluations should follow current best practices for handling missing baseline and outcome data.
Note that the Teen Pregnancy Prevention Evidence Review will accept any missing data method endorsed by the What Works Clearinghouse. The LES team’s current understanding of best practice is described here: https://ies.ed.gov/ncee/wwc/Docs/Multimedia/WWC-Missing-Data-508.pdf.
Missing values for covariates – i.e., covariates that will be included in the impact model to improve precision or to control for baseline differences (e.g., case deletion, dummy variable method, and imputation method).
2.5.2 Approach to hypothesis testing
Evidence thresholds
Expectation
1C.1:
For each primary contrast, the pre-specified analysis plan should
include the cutoff for statistical significance.
Two-sided hypothesis test: A statistical test in which the alternative hypothesis, Ha, states that the parameter of interest is different from the value specified in the null hypothesis, H0. (In impact analyses the null hypothesis value is usually zero) This means that the parameter can be either less than or greater than the value specified in the null hypothesis, H0, but the test does not specify which direction. One-sided hypothesis test: A statistical test in which the alternative hypothesis, Ha, specifies that the parameter of interest is greater (or less) than the value specified in the null hypothesis, H0. |
Strategy for dealing with multiple comparisons
Describe whether you plan to adjust for multiple comparisons in your reporting and, if so, the basis for the adjustment. Describe the method that you will use to adjust for multiple comparisons (e.g., Benjamini-Hochberg).1
If more than one primary contrast is specified, you must adjust for multiple comparisons in your analysis. If more than one secondary contrast has been specified, multiple comparisons adjustments are not required but you could choose to specify such an adjustment either (1) within each outcome domain; or (2) across all secondary contrasts. If you are not planning to correct for multiple comparisons, this should be stated clearly in this section along with a rationale explaining the decision.
Testing more than one contrast will lead to a greater likelihood of mistakenly concluding that the differences in means for outcomes of interest between the intervention and comparison groups are significantly different from zero (called Type I error in hypothesis testing). Strategies for minimizing multiple comparisons include limiting primary analysis to one contrast or applying an acceptable adjustment such as the Benjamini-Hochberg correction. |
Expectation
1C.1:
If there is more than one primary contrast, the plan should specify
a strategy for minimizing or adjusting for multiple comparisons.
2.5.3. Attrition and baseline equivalence
Attrition (RCTs only)
For studies in which individuals are randomly assigned to treatment and control conditions, describe your plans for calculating attrition at the individual level. For each wave of follow-up data collection, you should assess both overall attrition (total sample loss between randomization and follow up, as a percentage of the randomized sample), and differential attrition (percentage point difference in attrition between the treatment and control group).
For studies in which clusters are randomly assigned to conditions, describe your plans for calculating overall and differential attrition of both clusters and individuals at each wave of follow-up data collection. A cluster has attrited if no outcome data from any individuals in the cluster was obtained and used in the impact analysis. For calculating attrition of clusters, the reference group is the clusters that were randomly assigned. In order to calculate attrition of individuals, you will need to define the reference group from which attrition will be calculated. Typical reference groups are a) individuals that were enrolled in (or belonged to) clusters prior to random assignment of the clusters (or prior to a time when individuals could have known the treatment status of the cluster); or b) Individuals enrolled in (or belonging to) clusters shortly after random assignment of clusters. Attrition of individuals should only be calculated for the individuals in non-attriting clusters. If a cluster has attrited, it is counted in the calculation of cluster-level attrition and not in the individual attrition calculation. The individuals from that cluster should be excluded from the reference group for calculating individual attrition and should not be included in the attrition calculation of individuals.
Exhibit 2 in the Standards for Rigor provides the thresholds for both overall and differential attrition rates under which an RCT is considered to have low attrition per the Standards for Rigor. If individual-level or cluster-level attrition is beyond these thresholds, then the study will be considered a quasi-experimental design for the purpose of establishing baseline equivalence.
Attrition occurs when eligible units (schools, students) are randomly assigned but, for whatever reasons, data is not collected from them. Significant amounts of attrition from either the intervention or comparison/control group or both groups can compromise the initial comparability of the groups resulting from random assignment and potentially lead to biased estimates of the intervention’s impact. Tip: Because some readers and evidence reviews may want to calculate attrition themselves, the LES team recommends reporting the number randomized and the number included in the analytic sample, by treatment arm, for each contrast. |
Expectation
2A.2.b,c:
Attrition
in randomized controlled trials.
The study should calculate attrition appropriately, and incorporate
strategies designed to keep attrition within an acceptable range.
The sample used for the calculation of attrition is defined as the
number of individuals who are present for the follow up outcome
measurement as a percentage of the total number of members in the
sample at the time that individuals learned the condition to which
they were randomly assigned. This guideline includes an assessment
of both overall attrition (total sample loss between randomization
and the post-test), and differential attrition (percentage
difference in attrition between the treatment and control group).
In cluster-level designs (e.g., schools are randomly assigned) with
individual-level analysis (e.g., students), attrition will be
assessed for both cluster-level units and for individual units;
however, attrition is not double-counted across levels of analysis.
For example, if a school that serves 100 students drops out of a
study, and no outcome data can be collected from students in the
schools, attrition will only be counted at the cluster level, and
the 100 students will be removed from the denominator in the
assessment of individual-level attrition.
Assessing baseline equivalence
Describe your plans for assessing whether the treatment and control/comparison groups that comprise the analytic sample for the impact analysis are equivalent at baseline for each pre-specified contrast. (The analytic sample is comprised of the same treatment and control units that are included in impact analysis). Establishing baseline equivalence is required for primary contrasts in QEDs and high-attrition RCTs. Although it is not a requirement of the Standards for Rigor, the LES team recommends also establishing baseline equivalence for secondary contrasts, to ensure that any findings are reviewable by the TPPER.
Tip: Although RCTs with low attrition do not need to demonstrate baseline equivalence, the LES team recommends that you specify plans for assessing baseline equivalence in the analytic sample in case attrition exceeds low levels (see Exhibit 2 in the Standards for Rigor). |
The recommended method is to estimate the baseline treatment-control difference using a model with the same structural components as the impact model (e.g., block (stratum) dummies, random terms, treatment group indicator), but where the pre-test is the dependent variable, and other covariates that would appear in the impact model are omitted. In this approach, the coefficient for the treatment indicator will be the treatment-control difference on the pre-test measure. It is also acceptable to calculate the T-C difference by calculating the mean baseline score in the treatment group and the comparison group and subtracting the comparison mean from the treatment mean to obtain a difference.
However, the T-C difference is calculated, you should also standardize the reported baseline T-C difference by dividing that difference by the pooled (combined treatment and comparison group) standard deviation of the pretest or, for binary outcomes, you may choose to standardize using the Cox Index. This standardized difference is the one you should compare with the baseline equivalence thresholds in the Standards for Rigor.
For cluster design studies, standardize the baseline treatment-comparison group difference using the standard deviations of baseline measures of individuals, if possible. If the data are cluster-level aggregates of individual-level data, and the standard deviation of the individual-level data are not available, then report the standard deviations of the cluster-level measures and standardize the baseline treatment-comparison group difference relative to those standard deviations. Just be sure to clearly state that the standard deviations reported are cluster-level standard deviations.
Tip: for continuous measures, the LES team recommends reporting the standard deviation of the baseline measures for both the treatment group and the comparison/control group, because the TPPER may standardize the reported baseline group difference by dividing that difference by the pooled standard deviation of the baseline measure. |
Expectation
2A.3.a,b:
Baseline
Equivalence in the Analytic Sample – only for QED designs.
A QED should demonstrate that prior to the intervention, the
intervention and comparison groups were equivalent on observable
characteristics, to minimize potential bias from the choice to
participate in the intervention. This should be established for the
analytic sample, that is, the study units (e.g., schools,
classrooms, individuals) that remain at the end of the study when
the outcomes are assessed, rather than the initial groups in the
study. For each outcome, assessment of baseline equivalence in the
analytic sample means that the exact same records that are used in
the impact analysis are used for the baseline equivalence analysis.
This means that each unit in the impact and baseline equivalence
analyses must have non-missing values for both the baseline and the
outcome measure. Evaluations
must demonstrate that the intervention and comparison groups were
similar at baseline (p > .05, two-tailed test) on three key
demographic characteristics: age or grade level, gender, and
race/ethnicity. The study authors must also establish baseline
equivalence on each primary outcome measure (if available). Because
statistical significance is largely a function of sample size (i.e.,
it is difficult to detect statistically significant differences when
sample sizes are small), effect sizes should also be used to assess
baseline equivalence. For best practice, baseline differences
between treatment and comparison groups should not exceed a
standardized mean difference of .25 SD. Regardless of the size of
the baseline difference, each analytic model should include as
covariates the baseline measure of the outcome of interest (if
available) as well as the three key demographic characteristics
described above.
For
outcomes where there is no natural baseline measure, where
eligibility dictates that the baseline value is zero (e.g., an
intervention designed only for youth who have never been sexually
active), or for behavioral outcomes measured for youth below the age
of 14, it may be impossible to demonstrate baseline equivalence
using a baseline measure of the outcome. In such cases, it should be
established using a measure of knowledge, intentions, skills, or
attitudes. Baseline
Equivalence for Cluster QEDs.
If a quasi-experimental design uses cluster-level assignment but has
individual-level data and will show that treatment and comparison
group individuals were equivalent at baseline, the QED will be
assessed using the baseline equivalence guideline above. However, it
may also be acceptable to show that clusters were equivalent at
baseline. There are two acceptable ways to show that clusters are
equivalent at baseline: (see Standards
for Rigor
for
additional details).
2.5.4 Analytic approach
Modeling approach for primary research questions
Describe, in plain language, your overall modeling approach. For example, will similar (e.g., linear) regression models be used for all contrasts? For continuous and binary outcomes? Will impacts be estimated separately at each follow-up time point? If applicable, how will you account for clustered data?
Tip: it is often acceptable to use a single modeling approach for all contrasts in a study. Many impact evaluations use linear probability models (or hierarchical linear models) for both continuous and binary outcomes because they are easy to interpret. |
Model specification for primary research questions
Provide one or more model specifications (e.g. “Greek models”) that correspond to the pre-specified primary contrasts. A single model specification may be relevant to all of the planned contrasts, or different models may be needed for different types of contrasts. In the model specifications, show:
A term representing the dependent variable
A term representing the treatment indicator (i.e. the right-hand-side model term that produces the estimate of program impact on the outcome)
For models where the treatment indicator is interacted with other model terms (e.g., with randomization blocks), provided an explanation of how the multiple treatment terms will be averaged to produce a single, overall impact estimate
Terms representing covariates
Terms that represent design factors (e.g., randomization or matching blocks, or terms to account for the clustering of students in schools)
Provide a narrative description of the Greek models including:
Explanation of variables and subscripts
Interpretation of key parameters, especially the parameter that will produce an impact estimate
Explanation of terms that are included to account for blocking or matching
Explanation of terms that are included to account for clustering
For example, the unit of analysis might differ from the unit of assignment to the intervention, such as when classrooms are assigned to treatment or control conditions, but outcomes are measured at the student level
Below is an example of what a well-specified Greek model might look like. (You do not have to use this format and your model specification may be different than this one). This example is for a blocked individual-level RCT with students randomly assigned within CBOs:
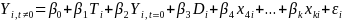
Where:
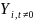 is the outcome of interest (e.g. consistent condom use) for student i
at time t
is the outcome of interest (e.g. consistent condom use) for student i
at time t
Ti is a dummy variable equal to 1 if student i was assigned to the treatment group
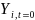 is the baseline measure of the outcome of interest (e.g. consistent
condom use) for student i
is the baseline measure of the outcome of interest (e.g. consistent
condom use) for student i
Di is a CBO dummy (which accounts for blocking by CBO)
Xmi is the mth baseline characteristic or control variable for student i (e.g. =1 for males).
The coefficient on the treatment dummy, β1, is the primary coefficient of interest. For an unfavorable outcome (e.g. teen pregnancy), a negative and statistically significant coefficient would be interpreted to mean that the program was effective in reducing the rate of that outcome.
Covariates
Provide a detailed description of covariate selection. Note particularly whether the final selection of covariates is theory-driven, data-driven (e.g., an elimination procedure), or some combination. You should state that you have made an a priori decision that the pre-test measure of the outcome will be included in the model along with age or grade level, gender, and race/ethnicity. For other covariates, if an elimination procedure is planned, state the thresholds for inclusion/exclusion (e.g., covariates with p-values <0.20 will be retained in the final model).
Do not include “endogenous” covariates in the impact model. Covariates should either be measured before treatment begins or be measures whose values cannot be influenced by the treatment (e.g., treatment cannot change a person’s age).

Expectation 2A.1.d: At a minimum, regression models used to estimate program impacts should control for a baseline measure of the outcome of interest, if available, as well as baseline measures of three key demographic characteristics: age or grade level, gender, and race/ethnicity.
Specify the software package(s) and versions that will be used to fit the regression models described above.
Subgroups (optional)
Describe any subgroups for which you will conduct additional impact analyses (e.g., teen parents, female youth, racial/ethnic subgroups, youth sexually active at baseline, etc.).
If the subgroups for which treatment effects will be computed vary across outcomes or follow-up periods, clarify for which combinations of outcomes and follow-up periods the subgroup effects will be estimated
Describe how the subgroup analyses will be conducted, for example, by
including interaction terms in the model or
estimating impacts for an individual subgroup (e.g., girls) or separately for the subgroups (e.g., separately for girls and boys)
Either explain in the narrative if and how the overall impact model specified above will differ for the subgroup analyses, or provide an example of the Greek model that will be used to test for subgroup impacts along with a brief narrative explaining the model.
Tip: the TPPER will only review and summarize impact results for subgroups defined by (1) gender or (2) sexual experience at baseline. The TPPER will not report the results of tests for the difference between two subgroups (e.g., the TPPER will not report results of a test of whether impacts were different for boys versus girls). |
Statistical power analysis
Present a power analysis for two outcomes showing the proposed sample size will support adequate statistical power to detect program impact/effects. (For studies with two or more primary outcomes, the power analysis should focus only on two of those primary outcomes. If your study has only one primary outcome, please present a power analysis for that outcome and one secondary outcome.) Along with the Minimum Detectable Impact (MDI) and Minimum Detectable Effect Size, please make sure to report the following assumptions (if your assumptions have not changed, you may copy and paste the power analysis from section 2.5.4 of your approved evaluation plan into this section):
The level of significance (usually 0.05 percent)
The number of sides of the test (usually two-tailed)
The power (usually 80 percent)
The size of the analytic sample (i.e., the number of treatment and control group members at follow up)
For binary outcomes, the mean of the outcome
For continuous outcomes, the standard deviation of the outcome
The R-squared (i.e., proportion of outcome variance explained by covariates)
For cluster RCTs, the intraclass correlation coefficient (ICC)
For cluster RCTs, the proportion of group-level outcome variance explained by covariates
For additional information on power analysis, see https://opa.hhs.gov/sites/default/files/2020-07/mdi-tabrief.pdf or the LES team’s power analysis webinar slides and recording.
Tip: When conducting your power analyses, make sure that you factor in the response rates that you anticipate achieving. For example, if your baseline sample size is 1,000 (500 treatment group members and 500 control group members) and you expect an 80% response rate on the long-term follow up survey, your power analysis should use assume a sample size of 800 (400 treatment and 400 control group members). Your LES Liaison can provide support and additional resources for conducting a power analysis. |
2.5.5 Differences in approach for secondary contrasts
Specify your procedures for conducting analyses to address secondary contrasts, if they differ from the procedures described above. If analytic approaches for primary and secondary contrasts are identical, note that here.
2.5.6 Summary of contrasts
Update the description of the test(s)/contrast(s) (from section 2.5.2 of your evaluation plan) that will answer each of your research questions, and note whether the test is primary (i.e., those upon which you will draw outcome evaluation conclusions) or secondary (i.e., those that might provide additional suggestive evidence). To help complete this section, we suggest completing the contrast table in Appendix B. If you have not made any changes to your contrasts, you can copy/paste Section 2.5.2 of your original evaluation plan into Section 2.5.6 (this section) and Appendix B of your revised evaluation plan.
2.5.7 Reporting results
Specify how you anticipate presenting impact results in your final impact evaluation report that will be submitted to ACF, using table shells. The table shells should reflect the decisions you have made about what types of information to report (e.g., will the team report T and C group means and the regression-adjusted difference? Standard errors? Confidence intervals? P-values? Sample sizes?) as well as the format for displaying the information (e.g., separate tables for each follow up period or one table showing results for both short- and long-term follow ups).
Below are some examples of what a table shell might look like. (You do not have to use any of these formats):
Table Shell for Impacts: Example 1 (Binary outcomes – reporting in original metric of the data)
Outcome |
Treatment Group Mean |
Control Group Mean |
Impact |
Standard Error |
Relative
Impact |
95% Confidence Interval |
Outcome 1 |
||||||
3-month follow-up |
0.60 |
0.55 |
0.05** |
0.01 |
8% |
[0.01, 0.09] |
12-month follow-up |
0.60 |
0.55 |
0.05** |
0.01 |
8% |
[0.01, 0.09] |
Outcome 2 |
||||||
3-month follow-up |
0.60 |
0.55 |
0.05** |
0.01 |
8% |
[0.01, 0.09] |
12-month follow-up |
0.60 |
0.55 |
0.05** |
0.01 |
8% |
[0.01, 0.09] |
Notes. This table reports the adjusted treatment group mean, control group mean, and difference between the treatment and control groups. Regressions include controls for age/grade, race/ethnicity, gender, and the outcome of interest at baseline. Robust standard errors are reported. Statistical significance, based on difference between research groups: *** 1 percent level; ** 5 percent level; * 10 percent level.
Table Shell for Impacts: Example 2 (Binary outcomes – reporting percentages who responded affirmatively)
Outcome |
Short-Term Impacts |
Longer-Term Impacts |
|
||||||||||
Adjusted Treatment Meana |
Unadjusted Control Mean |
Treatment Effectb |
p-Value |
Adjusted Treatment Meana |
Unadjusted Control Mean |
Treatment Effectb |
p-Value |
|
|||||
Domain 1 (percentage responding affirmatively) |
|||||||||||||
Outcome 1 |
28.02 |
28.14 |
-0.11 |
.946c |
35.95 |
34.35 |
1.59 |
.378c |
|||||
Outcome 2 |
8.73 |
8.99 |
-0.25 |
.815c |
12.09 |
11.64 |
0.45 |
.719c |
|||||
Domain 2 (percentage responding affirmatively) |
|||||||||||||
Outcome 1 |
n/a |
n/a |
n/a |
n/a |
5.53 |
5.91 |
-0.38 |
.683d |
|||||
Source: Follow-up surveys administered 6 months after baseline and 12 months after baseline.
Notes: Short-term results in this table are based on 2,665–2,667 respondents who provided valid survey responses to relevant items. Longer-term results are based on 2,720–2,780 respondents who provided valid responses to relevant items.
a The treatment group mean is regression adjusted, calculated as the sum of the unadjusted control group mean and the regression-adjusted impact estimate (treatment effect).
b The treatment effect was estimated in a multi-level model that controls for randomization blocks and other covariates. The treatment effect is expressed as a difference in percentage points. Due to rounding, reported treatment effects may differ from differences between reported means for the treatment and control groups.
c . After application of a Benjamini-Hochberg (1995) correction for two tests within this outcome domain, the criterion for statistical significance is p<.05 if both tests have p-values less than .05, and .025 if only one of the two tests has a p-value less than .05.
d Criterion for statistical significance is p<.05.
Table Shell for Impacts: Example 3 (Continuous scale outcomes)
Outcome |
Adjusted Treatment Meana |
Unadjusted Control Mean |
Treatment
|
SESc |
p-Value |
|
Short-Term Follow-Up |
||||||
Outcome 1 |
3.18 |
3.13 |
0.05 |
*** |
0.13 |
.000 |
Longer-Term Follow-Up |
||||||
Outcome 1 |
3.16 |
3.13 |
0.03 |
* |
0.08 |
.027 |
Source: Follow-up surveys administered 6 months and 12 months after baseline.
Note: Results in this table are based on 2,675-2,688 respondents (short-term survey) and 2,790–2,799 respondents (longer-term survey) who provided valid survey responses to relevant items.
a The treatment group mean is regression adjusted, calculated as the sum of the control group mean and the regression-adjusted impact estimate (treatment effect).
b The treatment effect was estimated in a multi-level model that controls for randomization blocks and other covariates. The treatment effect is expressed in the original metric of the outcome variable. Due to rounding, reported treatment effects may differ from differences between reported means for the treatment and control groups.
c The SES is the standardized effect size of the difference. The SES is the treatment effect divided by the pooled standard deviation of the treatment and control groups.
* p<.05, ** p<.01, *** p<.001 (two-tailed tests).
2.5.8 Sensitivity analysis (optional)
Describe any analyses you will conduct to test the robustness of the findings to alternative assumptions or specifications of the analytic model. Neither the TPPER nor the Standards for Rigor require sensitivity analyses. However, demonstrating that your results are robust to alternative specifications will lend credibility to your findings. For example, if you are using multiple imputation to address missing outcome data, you may wish to test whether your primary findings hold up if you instead use non-response weights or conduct a complete case analysis. Another example would be to test an alternative specification of your analytic model—for instance if you use linear probability models for all contrasts in your main analysis, you may wish to test whether using a nonlinear model such as logit or probit for binary outcomes affects the impact estimates or confidence intervals. Again, finding similar results using different specifications will help you to make a stronger case that your findings are the right ones.
Note that the analysis plan does not necessarily need to detail all sensitivity analyses that might be conducted. It is common for questions or doubts to arise as the analysis proceeds, which could be addressed by conducting and reporting a sensitivity analysis. You may conduct such analyses even if they were not specified in the analysis plan.
Sensitivity analyses are additional analysis conducted using different assumptions from those made for the primary analyses. Sensitivity analyses can help assess how robust your findings are to the assumptions and decisions made to address the primary analyses. |
Appendix B. Contrast Table
Update the contrast table included in your evaluation plan for each of your research questions as needed. (Note that the LES team provided a contrast table for your primary contrasts in your evaluation plan approval memo.)
Below we provide an example contrast table, including two research questions.
Research Question: Primary/ Secondary |
Design |
Target Population* |
Sample Eligibility Criteria |
Treatment Group |
Comparison Group |
Outcome |
Baseline (if applicable) |
|||
Treatment Description* |
Condition/ Description* |
Domain* |
Unit
of assignment/ observation: |
Timing of measurement |
Unit
of assignment/ observation: |
Timing of measurement |
||||
RQ 1 |
RCT |
High school freshmen in low-performing schools |
All students enrolled in health classes in participating schools |
Innovative Program A |
Business as usual |
Sexual intercourse |
Individual participants: Survey – sexual intercourse in past month |
6 months and 12 months after random assignment |
Individual participants: Survey – sexual intercourse in past month |
Immediately prior to random assignment |
RQ 2 |
RCT |
High school freshmen in low-performing schools |
All students enrolled in health classes in participating schools |
Innovative Program A |
Business as usual |
Unprotected sex |
Individual participants: Survey – sex without a condom in past month |
6 months and 12 months after random assignment |
Individual participants: Survey – sex without a condom in past month |
Immediately prior to random assignment |
* Indicates one of the four components of your impact evaluation research questions
Example Research Question 1: To what extent did six weeks of Innovative Program A reduce the incidence of sexual intercourse among high school freshmen compared to high school freshmen who did not receive the intervention?
Example Research Question 2: To what extent did six weeks of Innovative Program A reduce the incidence of unprotected sex among high school freshmen compared to high school freshmen who did not receive the intervention?
Appendix C: Detailed specification of measures to be analyzed
Complete the table below for all primary and secondary outcomes and add this appendix to the end of your evaluation plan. Below we provide an example for three different outcomes.
Outcome domain |
Outcome measure |
Survey items used to construct measure (including coding of responses and relevant skip patterns to demonstrate how the outcome measure will be defined for the full sample) |
Description of how survey items will be combined to construct measure (including coding of final construct) |
Sexual behavior |
Sexual intercourse, oral sex, or anal sex in last 90 days |
Q1: Have you ever engaged in sexual intercourse, oral sex, or anal sex? (1 = yes, 2 = no) If Q1 = 1 (yes): Q2: Have you engaged in sexual intercourse in the last 90 days? (1 = yes, 2 = no) If Q1 = 1 (yes): Q3: Have you engaged in oral sex in the last 90 days? (1 = yes, 2 = no) If Q1 = 1 (yes): Q4: Have you engaged in anal sex in the last 90 days (1 = yes, 2 = no) |
If Q2, Q3, OR Q4 = 1 (yes), then outcome = 1 (yes) If Q1 = 2 (no), then outcome = 0 (no) If Q2, Q3, AND Q4 = 2 (no), then outcome = 0 (no).
Outcome coded as 0 = have not had sexual intercourse, oral sex, or anal sex in last 90 days; or 1 = have had had sexual intercourse, oral sex, or anal sex in last 90 days |
Intentions to engage in sexual activity |
Intend to have sexual intercourse, oral sex, or anal sex in the next month |
Q1: Do you plan to have sexual intercourse in the next month? (1 = yes, definitely, 2 = yes, probably, 3 = probably not, 4 = definitely not) Q2: Do you plan to have oral sex in the next month? (1 = yes, definitely, 2 = yes, probably, 3 = probably not, 4 = definitely not) Q3: Do you plan to have anal sex in the next month? (1 = yes, definitely, 2 = yes, probably, 3 = probably not, 4 = definitely not) |
If Q1, Q2, OR Q3 = 1 or 2 (yes, definitely or yes, probably), then outcome = 1; if Q1, Q2, AND Q3 = 3 or 4 (probably not or definitely not), then outcome = 0.
Outcome coded as 0 = do not intend to have sexual intercourse, oral sex, or anal sex in next month; or 1 = intend to have sexual intercourse, oral sex, or anal sex in next month |
Gender attitudes and norms |
Girls to blame for mistreatment2 |
Q1. A girl wearing revealing clothing deserves to have comments made about her. (0 = Strongly disagree, 1 = Disagree, 2 = Agree, 3 = Strongly agree) Q2. If a girl is forced to have sex it is often because she did not say "no" clearly enough. (0 = Strongly disagree, 1 = Disagree, 2 = Agree, 3 = Strongly agree) Q3. In a sexual relationship, it is mainly a girl’s responsibility to make decisions about birth control. (0 = Strongly disagree, 1 = Disagree, 2 = Agree, 3 = Strongly agree) Q4. Girls who cheat on their boyfriends deserve to be hurt physically. (0 = Strongly disagree, 1 = Disagree, 2 = Agree, 3 = Strongly agree) Q5. Girls who cheat on their boyfriends deserve to be hurt emotionally. (0 = Strongly disagree, 1 = Disagree, 2 = Agree, 3 = Strongly agree) Q6. Girls should get turned on when a guy is rough with them. (0 = Strongly disagree, 1 = Disagree, 2 = Agree, 3 = Strongly agree) Q7. Girls usually say no to sex when they really mean yes. (0 = Strongly disagree, 1 = Disagree, 2 = Agree, 3 = Strongly agree) Q8. It is a girl’s responsibility to avoid getting pregnant. (0 = Strongly disagree, 1 = Disagree, 2 = Agree, 3 = Strongly agree) |
If the respondent answered 6 or more (75%) of the 8 items, take the mean of all items. If the respondent answered 5 or fewer of the items, the outcome is missing. Outcome ranges from 0 to 3, with higher values indicating a higher level of agreement with the concept that girls are to blame for mistreatment. |
1 Under version 4.1, the What Works Clearinghouse used the Benjamini-Hochberg correction to adjust for multiple comparisons (see “WWC Procedures Handbook, Version 4.0,” Section VI Reporting on Findings: Subsection 3, “Statistical Significance of Findings” (p. 21)). In version 5.0, the WWC will determine effectiveness ratings at the outcome domain level by creating a domain-level composite finding, eliminating the need for a multiple comparisons adjustment. PREIS evaluations could consider a similar approach.
2 Welti, Griffith & Manlove (2021) developed the scale using the Child Trends Manhood 2.0 Program Evaluation Baseline Survey and demonstrated reliability (Chronbach’s alpha = 0.83).
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | Abt Single-Sided Body Template |
| Author | Charmayne Walker |
| File Modified | 0000-00-00 |
| File Created | 2024-12-24 |
© 2025 OMB.report | Privacy Policy