1205-0453_NAWS_Supporting Statement Part B _for CEO Review (4)_12.06.2024
1205-0453_NAWS_Supporting Statement Part B _for CEO Review (4)_12.06.2024.docx
National Agricultural Workers Survey
OMB: 1205-0453
[1205-0453: The National Agricultural Workers Survey, Part B]
Collection of Information Employing Statistical Methods
The objective of the National Agricultural Workers Survey (NAWS) is to provide descriptive statistics of the characteristics of crop workers using a statistical methodology designed to address the difficulties of surveying a mobile and seasonal population often living in non-standard and sometimes hidden housing.1 In addition, the NAWS is designed to address the information needs of various Federal agencies that oversee farm worker programs. These stakeholders include agencies concerned with assessing agricultural productivity, international transaction accounts, and migrant and seasonal farm worker health and education. Another purpose of the NAWS is to produce accurate regional estimates of the share of farm workers who are eligible for training and employment services through the Employment and Training Administration’s (ETA) National Farmworker Jobs Program (NFJP).
Respondent Universe and Samples
Respondent Universe
The universe for the NAWS is the population of workers active in crop agriculture in the continental United States. Since the NAWS samples crop workers at the worksite, the definition of the respondent universe involves the definitions of both an eligible employer and an eligible worker.
The universe of eligible employers includes all employers in North American Industry Classification System (NAICS) codes 111 and 1151. NAICS code 111 is Crop Agriculture, which includes employers hiring workers on farms and ranches or in greenhouses. NAICS code 1151 is Support Activities for Crop Production, which includes employers such as farm labor contractors, custom harvesters, and crop-dusting companies who contract with agricultural producers to supply support services and hire workers to carry out these contracts at farms, ranches, and greenhouses. Eligible employers must have workers who are actively engaged in crop production.
Eligible workers must be employed by an eligible employer and have worked for that employer for at least four hours on a single day in the prior 15 days. Workers in a packing operation are eligible to be interviewed if the canning or packing plant is adjacent to or located on a farm and at least 50 percent of the produce being packed or canned originated from the farm of the contacted grower.
The following criteria define ineligible employees at an otherwise eligible employer. The employee is ineligible if he/she:
Was interviewed in the NAWS within the last 12 months in the same location.
Has not worked for the contacted employer for four hours or more on at least one day in the last 15 days.
Does “non-farm work” for the employer (e.g., mechanic, sales, office).
Is a family member of the employer and does not receive a paycheck.
Is the employer (grower or contractor).
Is a sharecropper that makes all operational decisions such as when, where, and how to plant or harvest.
Works for a landscaping company that only sells, installs, maintains, or preserves trees or plants. This includes the planting of ornamental plants and placement of sod.
Samples
The NAWS uses a complex sampling design including both stratification and clustering. The population of interest is the crop labor force, including migrant and seasonal workers, where the crop worker is the elementary unit. Multi-stage sampling is implemented to randomly select and interview approximately 1,500 crop workers. Since migrant and seasonal crop workers are a mobile and time-sensitive population, the sampling design utilizes both geographic and temporal strata. Within each stratum, there is clustering. The primary sampling unit is the Farm Labor Area (FLA) (county cluster). Samples of employers and of workers within employers are also selected. This section describes the stratification, primary sampling units, and employer and worker universe size and samples for the survey (see Table 1). Section 2 provides more details on the statistical methods used in sampling.
Table 1: NAWS Stratification and Sampling Units
Entity |
Universe |
Sample |
Cycle |
3 |
3 |
Agricultural Region |
12 |
12 |
Farm Labor Area |
928 |
105 |
Crop Worker Employer |
269,000* |
395 |
Crop Worker |
1,645,000* |
1,500 |
*Estimate, rounded to the nearest thousand.
Stratification
To account for seasonal and geographic variation in farm employment, the year is divided into three four-month cycles: October through January, February through May, and June through September. The NAWS sampling will use 12 distinct agricultural regions based on the United States Department of Agriculture’s (USDA) 17 regions. Table 2 shows the correspondence between USDA and NAWS regions. At the start of the survey in 1988, the 17 USDA regions were collapsed into 12 NAWS regions by combining smaller regions that were similar (e.g., Mountain I and Mountain II) based on statistical analysis of cropping patterns. This reduced the number of regions and increased the size of the smallest strata.
Table 2: Correspondence between NAWS and USDA Regions
NAWS Sampling Region |
USDA Region Code & Name |
States in USDA Region |
Appalachian I, II (AP12) |
Appalachian I |
NC, VA |
Appalachian I, II (AP12) |
Appalachian II |
KY, TN, WV |
Corn Belt Norther Plains (CBNP) |
Corn Belt I |
IL, IN, OH |
Corn Belt Norther Plains (CBNP) |
Corn Belt II |
IA, MO |
Corn Belt Norther Plains (CBNP) |
Northern Plains |
KS, NE, ND, SD |
California (CA) |
California |
CA |
Delta Southeast (DLSE) |
Delta |
AR, LA, MS |
Delta Southeast (DLSE) |
Southeast |
AL, GA, SC |
Florida (FL) |
Florida |
FL |
Lake (LK) |
Lake |
MI, MN, WI |
Mountain I, II (MN12) |
Mountain I |
ID, MT, WY |
Mountain I, II (MN12) |
Mountain II |
CO, NV, UT |
Mountain III (MN3) |
Mountain III |
AZ, NM |
Northeast I (NE1) |
Northeast I |
CT, ME, MA, NH, NY, RI, VT |
Northeast II (NE2) |
Northeast II |
DE, MD, NJ, PA |
Pacific (PC) |
Pacific |
OR, WA |
Southern Plains (SP) |
Southern Plains |
OK, TX |
The annual sample will include all 12 regions for each of the three cycles. The USDA’s Farm Labor Survey (FLS) provides quarterly estimates of the size of the directly hired crop labor force including H-2A workers, the Bureau of Labor Statistics’ Quarterly Census of Employment and Wages (QCEW) provides quarterly estimates of the number of crop workers employed by labor contractors, and H-2A case disclosure data from the Office of Foreign Labor Certification (OFLC) provides the number of H-2A temporary agriculture workers employed by labor contractors and associations. The sum of data from these sources form estimates of the size of the crop labor force in each region-cycle stratum. The NAWS region definitions and the FLS regions are congruent. Quarterly data are reapportioned into the three NAWS cycles. Table 3 shows the estimated crop labor force in each region-cycle stratum in FY 2023.
Table 3. Estimated Crop Labor Force (1000s) by region and cycle*
Region |
Fall |
Winter/ Spring |
Summer |
Northeast I |
29.6 |
26.6 |
35.5 |
Northeast II |
41.9 |
23.9 |
41.0 |
Appalachia I/II |
54.3 |
40.4 |
62.5 |
Florida |
47.8 |
44.3 |
46.1 |
Delta/Southeast |
73.0 |
53.7 |
77.9 |
Lake |
44.7 |
33.4 |
48.4 |
Corn Belt/Northern Plains |
97.3 |
65.6 |
92.7 |
Southern Plains |
40.1 |
41.5 |
44.1 |
Mountain I/II |
32.1 |
27.2 |
43.2 |
Mountain III |
28.6 |
26.3 |
18.4 |
Pacific Coast |
138.4 |
82.5 |
161.9 |
California |
439.5 |
397.1 |
494.2 |
TOTALS |
1,067.2 |
862.3 |
1,166.0 |
*Table derived from 2021-2022 FLS data, 2021-2022 QCEW data, and 2023 H-2A Case Disclosure data. Values may not add exactly due to rounding.
Primary Sampling Unit
The primary sampling unit is the Farm Labor Area (FLA), a geographic unit consisting of one or more counties based on farm labor usage patterns. Each of the 3,067 counties in the continental United States is assigned to one of 928 FLAs. In the West, many FLAs consist of a single agriculture-intensive county, while in other parts of the country FLAs include two or more counties, each with less worker-intensive farming or low agricultural output compared to the national average.
ETA updated the FLAs in 2020; they are defined using 2017 CoA and QCEW data and account for major geographic barriers and freeways to ensure the ability to travel within a FLA. ETA will update the FLAs again in 2025, upon receiving special tabulations of 2022 CoA data.
For each of the three annual interview cycles, NAWS staff will select a sample of FLAs in each of the 12 regions using methods described in Section 2c below. NAWS interviewers plan to visit 106 FLAs across all region-cycle strata in FY 2025. 2
Employer and Worker Samples
The universe of crop employers is estimated to be 269,000. This estimate is derived by rounding to the nearest thousand the sum of agricultural employers from the 2022 CoA that directly hired crop workers (256,373), and the annual estimate of private-industry NAICS 1151 establishments from the 2022 QCEW (12,535). 3
The size of the crop employer sample necessary to perform 1,500 interviews is estimated to be 689. This estimate is calculated as the quotient of the target crop worker sample size (1,500) divided by the product of the average number of workers interviewed per farm in FY 2023 (4.1), the eligible employer rate, and the response rate of eligible employers. See 1205-0453 Supporting Statement Part A for a detailed explanation of the estimation method and a derivation of the parameter values.
Although there is no census of crop workers, the universe of the crop farm labor force, including crop workers who are seasonally employed with the H-2A visa, can be estimated using labor expenditure data from the CoA, wage data from the FLS, and hours per worker data from a combination of the FLS and the NAWS. Based on 2017 data from these sources, there are an estimated 1.6 million hired crop workers, including workers provided by farm labor contractors. This estimate will be revised upon receipt of special tabulations of 2022 CoA data.
Sample size
The NAWS faces several challenges in defining an optimal design. First, the NAWS has a complex sampling design that includes both stratification and clustering. Second, the NAWS uses administrative data that comes in clumps that are not optimal for some variables of interest. Third, surveys are generally optimized for one variable of interest and the NAWS collects data on over 250 variables of interest.
For complex survey designs, the design effect measures the efficiency of a sampling design that deviates from simple random sampling. The design effect for a variable of interest is defined as the ratio of the variance calculated under the complex design divided by the variance calculated under the assumption of a simple random sample. Design effects greater than one mean that the complex survey design delivers higher variance than a simple random sample. While it is possible to achieve a design effect of less than one, many factors can make a design less efficient. Lower design effects are generally achieved when strata are homogeneous and clusters are heterogeneous.
We calculated design effects for demographic and employment characteristics using the data collected for the NAWS in fiscal years 2019-2022. NAWS design effects varied from less than one to 20, depending on the variable. Generally, higher design effects are associated with both heterogeneous strata and relatively homogeneous clusters. This usually happens for variables that tend to be relatively similar within farms and FLAs, but heterogeneous in some regions, particularly in the East and Midwest. Examples of such variables include work force characteristics, place of birth, and visa status.
The NAWS design is more efficient for collecting information on worker’s household composition, key variables for estimating service program size, and immigration policy impacts. These types of variables have more heterogeneity within clusters and are more homogeneous within strata.
Originally, the NAWS design was driven by a single variable, the exit rate of newly legalized Special Agricultural Workers. Based on this requirement, the NAWS sample size was set at 2,500 interviews annually. This sample size was also sufficient to report national numbers on an annual basis. After the exit rate requirement was dropped, the sample size fluctuated between 1,500 and 3,260 interviews per year, which allowed for reporting national and regional information using two and four years of data, respectively.
Currently, the NAWS collects data for a variety of Federal agencies and Federal farm worker programs, two of which – NFJP and Migrant and Seasonal Head Start– draw on specific subpopulations. The NAWS has, since its inception, collected data that are used in the NFJP funding formula. The FY 2025 sampling calculations examine the sample sizes needed to report characteristics of crop workers who fall into four subpopulations:
The subpopulation of workers who are poor.
The subpopulation of workers who are authorized to work in the United States.
The subpopulation of workers who have taken or are taking adult education or training classes; and
The subpopulation of workers who have taken English or ESL classes, the most common types of courses taken by crop workers.
For each of these subpopulations, the first step in estimating the desired sample size is to calculate the sample size under simple random sampling (SRS) needed to produce estimates with the desired precisions (see Table 4). The sample size is calculated as:
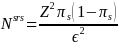
where,
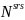 is the desired sample size under SRS,
is the desired sample size under SRS,
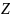 is the Z-score corresponding to a 95 percent confidence level, (1.96
for 95%),
is the Z-score corresponding to a 95 percent confidence level, (1.96
for 95%),
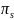 is proportion of the population belonging to subpopulation
is proportion of the population belonging to subpopulation
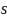 ,
and
,
and
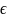 is the desired half-width (margin of error) of the confidence
interval.
is the desired half-width (margin of error) of the confidence
interval.
The proportion,
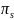 ,
is set to 0.5 to assume maximum variability and obtain the largest
possible sample size necessary to achieve a 95 percent confidence
interval with 5 percent margin of error. Hence, all other proportions
are assured to meet the desired precision.
,
is set to 0.5 to assume maximum variability and obtain the largest
possible sample size necessary to achieve a 95 percent confidence
interval with 5 percent margin of error. Hence, all other proportions
are assured to meet the desired precision.
Table 4, below, shows the additional
calculations needed to adjust the subpopulation sample sizes to
account for the NAWS’s complex sampling design. First, the
desired sample size for the subpopulation is calculated by
multiplying the SRS sample size,
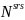 , by
the design effect for subpopulation
, by
the design effect for subpopulation
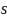 ,
,
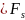 .
Design effects are calculated from several years of data and are
fairly stable. The desired NAWS sample size then considers the
expected proportion of subpopulation
.
Design effects are calculated from several years of data and are
fairly stable. The desired NAWS sample size then considers the
expected proportion of subpopulation
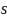 within the NAWS sample,
within the NAWS sample,
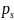 .
This number is based on previous NAWS data. The final number in the
calculation is the number of years of data that would ideally be
combined for reporting purposes for each subpopulation.
.
This number is based on previous NAWS data. The final number in the
calculation is the number of years of data that would ideally be
combined for reporting purposes for each subpopulation.
The desired annual sample size,
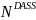 ,
can then be calculated using the following equation:
,
can then be calculated using the following equation:
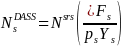
Where,
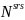 is the SRS sample size to achieve a 95 percent Confidence Interval
with the desired half-width,
is the SRS sample size to achieve a 95 percent Confidence Interval
with the desired half-width,
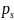 is the proportion of subpopulation
is the proportion of subpopulation
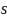 in the NAWS sample, and
in the NAWS sample, and
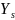 is the number of years of data to be combined for reporting on
subpopulation
is the number of years of data to be combined for reporting on
subpopulation
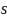 .
.
For example, in Table 4 below, the
SRS sample size (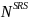 )
for workers who are authorized to work in the United States is 384.
With a design effect (
)
for workers who are authorized to work in the United States is 384.
With a design effect (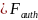 )
of 12.02, the subpopulation size within the NAWS sample (
)
of 12.02, the subpopulation size within the NAWS sample (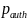 )
is 59 percent and the reporting frequency (
)
is 59 percent and the reporting frequency (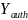 )
is every six years. Using the formula above, the result is a desired
annual NAWS sample 1,304.
)
is every six years. Using the formula above, the result is a desired
annual NAWS sample 1,304.
Table 4 shows the overall design-adjusted sample sizes needed to meet the data collection goals for these four subpopulations range from 1,304 to 1,493. The desired NAWS sample size of 1,500 interviews in FY 2025 is based on the highest of these sample sizes, rounded up. This sample size would achieve all of the sampling objectives.
Table 4. Subpopulation Sample Size Calculations*
Sub- population (s) |
Desired half-width
( |
Proportion
Being Estimated ( |
Sample
Size for 95% Confidence Interval Under SRS ( |
Design Effect ( |
Desired
Sub- population Sample Size within NAWS ( |
Current
Proportion of Sub- population
in the NAWS Sample ( |
Years of Data to Combine for Reporting ( |
Desired
Annual Sample Size
( |
Adult Education or training |
5% |
50.00% |
384 |
7.91 |
3,039 |
41% |
5 |
1,484 |
English/ ESL classes |
5% |
50.00% |
384 |
4.97 |
1,908 |
15% |
9 |
1,413 |
Work-Authorized |
5% |
50.00% |
384 |
12.02 |
4,615 |
59% |
6 |
1,304 |
Below Poverty |
5% |
50.00% |
384 |
9.55 |
3,669 |
25% |
10 |
1,493 |
* The values in the table do not multiply exactly due to rounding.
The desired annual NAWS sample size is distributed across the region-cycle strata proportionate to the crop worker population numbers from the FLS. See Table 5 below.
Table 5. Estimated Sample Size by Region and Cycle in FY 2025*
Region |
Fall |
Winter/ Spring |
Summer |
Northeast I |
15 |
13 |
18 |
Northeast II |
21 |
12 |
20 |
Appalachia I/II |
27 |
18 |
29 |
Florida |
21 |
22 |
18 |
Delta Southeast |
35 |
26 |
37 |
Lake |
22 |
15 |
22 |
Corn Belt/Northern Plains |
48 |
31 |
44 |
Southern Plains |
20 |
20 |
21 |
Mountain I/II |
16 |
13 |
21 |
Mountain III |
13 |
13 |
9 |
Pacific |
68 |
39 |
80 |
California |
218 |
194 |
244 |
Total |
524 |
416 |
563 |
*Note that numbers include a small amount of rounding error.
Statistical Methods for Sample Selection
Overview
The goal of the NAWS sampling methodology is to select a nationally representative, random sample of crop workers. Stratified multi-stage sampling will be used to account for seasonal and regional fluctuations in the level of farm employment. There are two levels of stratification: three four-month cycles and 12 geographic regions, resulting in 36 time-by-space strata. For each cycle, within each region, NAWS staff will draw a random sample of FLAs. Within each FLA, counties are the secondary level of sampling units, ZIP Code regions are the third, farm employers are the fourth, and workers are the fifth.
For each cycle, the number of interviews allocated to each region is proportional to the estimated seasonal number of crop workers employed in the region. The regional allocation is distributed proportionately across the sampled FLAs expected to be visited. Within each FLA, interviewers will visit the sampled counties and ZIP Code regions to contact employers and select a random sample of eligible workers employed on the day of the visit.
Stratification
Interviewing Cycles
To account for the seasonality of agricultural production, interviews are conducted in three cycles each year with each cycle lasting four months. The number of interviews conducted in each cycle is proportional to the estimated number of crop workers employed during the cycle. The seasonal agricultural employment figures are based on the FLS and QCEW. The FLS provides quarterly employment figures for the continental United States. These quarterly figures are pro-rated into the three interview cycles.
Regions
As mentioned in Section 1, in each cycle, all 12 regions are included in the sample. The number of interviews per region is proportional to the size of the seasonal farm labor force in a region at a given time of the year. The size of the seasonal labor force in each region is derived from FLS and QCEW quarterly regional data, which are pro-rated into the three cycles before being distributed to the regions.
Sampling within Strata
Farm Labor Areas
Sampling FLAs is a two-stage process. In the first step, a roster of ten FLAs will be drawn in each cycle-region stratum using probabilities proportional to the seasonal labor force for that stratum. NAWS staff will conduct systematic probability proportional to size (PPS) sampling of FLAs within regions using SAS PROC SURVEYSELECT. The size measure for the FLA seasonal labor force will be calculated using farm labor expenditure data obtained from the CoA and seasonal adjustment factors derived from the QCEW. The seasonal adjustment factors will be made by aggregating the QCEW’s reported monthly employment figures for the months that correspond to each of the NAWS cycles (e.g., June, July, August, and September for the summer cycle). The percentage of annual employment corresponding to each cycle is the FLA’s seasonal adjustment factor. Until special tabulations of 2022 CoA data are available, the size measure for the FLA labor force will be calculated by multiplying the FLA’s annual hired and contract labor expenditures from the 2017 CoA by the seasonal adjustment factor from the 2018 QCEW.
There is no data source containing accurate details of when and where local crop work is occurring that could provide accurate planning of the NAWS interviewing locations. The local timing and location of seasonal farm employment depends on changes in cropping patterns and weather conditions, including disasters such as a drought or flood. Failing to complete an interview allocation in a particular area is not unusual, even after consulting local experts. Thus, the number of FLAs needed to complete the interview allocation within a cycle-region stratum cannot be determined in advance.
The second stage in the two-stage FLA sampling process is the progression through the roster of ten FLAs drawn in the first stage, to complete the regional interview allocation. The roster of ten FLAs will be randomly sorted, and the interviewers will begin in the FLA at the top of the list. They will move to additional FLAs as needed to complete the interview allocation for the region by proceeding down the list, in order.
For planning purposes, the starting
number of FLA visits for the annual sample will be 105. To ensure
there will be an adequate number of FLAs visited in each region, a
minimum of two FLAs will be assigned in each region per cycle. Thus,
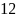 regions
regions
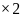 FLAs
FLAs
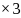 cycles
cycles
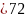 FLAs. Most of the remaining FLAs will be assigned to regions
proportionate to the size of the regions’ seasonal farm labor
force for a particular cycle, according to the FLS size numbers.
Additional FLAs will be allocated to regions where difficulty in
meeting interview allocations is anticipated, usually due to seasonal
factors. The starting number of FLAs selected for each cycle-region
stratum is anticipated to range from two to five.
FLAs. Most of the remaining FLAs will be assigned to regions
proportionate to the size of the regions’ seasonal farm labor
force for a particular cycle, according to the FLS size numbers.
Additional FLAs will be allocated to regions where difficulty in
meeting interview allocations is anticipated, usually due to seasonal
factors. The starting number of FLAs selected for each cycle-region
stratum is anticipated to range from two to five.
Since the exact number of FLAs visited each cycle is unknown until after a cycle is completed, the number of unique FLAs visited in a year is unknown until the end of the year.
Counties
Similarly, it is not possible to know in advance how crop workers are distributed within a FLA and the exact number of counties needed to encounter enough crop workers to complete the interview allocation. In most cases, interviews are completed in the first county and no additional counties are needed. However, because there is uncertainty about the number of workers in a county, additional counties may be needed to complete the interview allocation. Counties will be selected one at a time, without replacement, using probabilities proportional to the size of the farm labor expenditures in a county during a given season. Seasonality is considered constant within a FLA.
The process of selecting counties will begin with a randomly sorted list of the counties within the FLA. A cumulative sum of the size of the hired and contract labor expenditures, derived from CoA data, will be constructed for this list. When selecting a county, the selection number is the product of a random number selected from the uniform distribution, multiplied by the cumulative sum. The county that includes the selection number is chosen. Tables 6 and 7 illustrate an example of the algorithm used for selecting counties within FLAs.
Table 6: Example Counties and Labor Expenditures within an FLA
Counties in FLA |
Hired and Contract Labor Expenditures |
Cumulative Sum of Hired and Contract Labor Expenditures |
A |
100,000 |
100,000 |
B |
300,000 |
400,000 |
C |
800,000 |
1,200,000 |
D |
450,000 |
1,650,000 |
E |
600,000 |
2,250,000 |
Table 7: Example Showing Algorithm for Selecting Counties within FLAs
Step in the Algorithm |
Result |
Random number selected from uniform distribution |
0.657 |
Selection number (random number * cumulative sum of hired and contract labor expenditures) |
1,478,250 (0.657 * 2,250,000) |
County selected |
D |
As shown in the example in Tables 6 and 7, the cumulative sum of hired and contract labor expenditures for all counties in the FLA is 2,250,000. The random number selected from the uniform distribution is 0.657. The random number is multiplied by the cumulative sum of hired and contract labor expenditures to produce a selection number of 1,478,250. This selection number is included in the cumulative sum of county D, so county D is selected.
For timely field operations, several counties will be selected using the selection method above. Each county will be marked and ordered by its selection number (e.g., 1st, 2nd, 3rd). Interviews will begin in the first selected county, and when the list is exhausted, interviewers will move to the next randomly selected county on the list until all the allocated interviews in the FLA have been completed. In FLAs where crop work is sparse, interviewers may need to travel to several counties to encounter sufficient workers to complete the FLA’s allocation.
ZIP Code Regions
Sampled counties are divided into ZIP Code regions, which are smaller areas based on geographic proximity and the number of employers in the area. The purpose of ZIP Code regions is to group together employers that are close in proximity to reduce the cost of driving from employer to employer within a county. Counties can be comprised of a single ZIP Code region (for example, in the case of a small county) or multiple regions (for example, when a county is large). In a county with multiple ZIP Code regions, the goal is for the ZIP Code regions to be roughly equal in size.
The process of constructing the regions begins by randomly sorting the employers in the county by Zip Code and by a random number. Beginning at the top of the list, groups of seven employers are assigned as a Zip Code region. Some Zip Code regions may include growers from more than one Zip Code. For example, the last three employers in one Zip Code and the first three in the next Zip Code could comprise a Zip Code region. The final Zip Code region will be of unequal size if the number of growers in the county is not evenly divisible by seven. If there are five or six growers in the final group, it will stand alone as a Zip Code region. If the final group is four or fewer employers, it will be combined with the previous group. Thus, the final Zip Code region could vary in size from five to 11 growers.
When there are multiple ZIP Code regions in a county, the regions will be randomly sorted to produce a list that determines the order in which the areas will be visited. Interviewers will make three attempts to contact each agricultural employer in the first ZIP Code region on the list and then move down the list, following the random order, until the interview allocation is filled, or the county’s workforce is exhausted.
Employers
Lacking a universe list of crop employers, NAWS staff will compile a crop employer universe list using administrative lists, marketing lists, and online searches. The BLS provides names of agricultural employers in NAICS codes 111 and 1151 directly to the NAWS contractor per the terms of an agreement between the ETA and the BLS. Employers on the BLS list are those who pay unemployment insurance (UI) taxes. In states where UI is not mandatory for all agricultural employers, the list of employers from BLS will be supplemented with other sources.
One issue with the BLS lists is that farm labor contractors (FLCs) report payroll taxes from one location but work in multiple areas. Research has shown this is true for California FLCs, and since 2021 the list of FLCs is updated for counties in California. On the BLS list, FLCs report wages and pay unemployment insurance taxes in one location, which neglects that they may work in several counties throughout the state. The list only provides addresses and locations of FLCs in which they report, not the county/counties they primarily work in. To enrich the sampling frame, lists of California FLCs (from the Agricultural Commissioner’s office) were added to employer lists for counties that were selected as interview sites. This helps enrich the employer sampling list by providing a more accurate depiction of FLCs in California.
It is not possible to know in advance which employers will be active employers at the time of sampling. While NAWS staff relies on the best available information when preparing the employer sampling lists, several factors make it difficult to get an accurate list. First, there is a great deal of turnover in agricultural enterprises and lists are easily out of date. Second, as discussed above in the ZIP Code Regions section, seasons vary from year to year and employers change cropping patterns and practices, which in turn modifies labor utilization. Third, sources of farm employers are incomplete.
The policy for developing the employer list is to be more inclusive and allow employers on to the list who may have a low probability of eligibility. NAWS staff balances bias from exclusion of potentially eligible employers against lower response rates arising from the difficulty of screening and excluding ineligible employers. The employer list inclusion procedures tend to err on the side of inclusion of possibly inactive employers.
Employers are selected using simple random sampling for several reasons. First, there is no reliable information on employers’ workforce size before the interviewing cycle starts. As such, using PPS to select employers is not possible. Second, simple random sampling results in selection of a greater variety of farm sizes, whereas PPS favors larger farms.
Because of uncertainty about the conditions of local seasonal farm labor, the number of eligible employers in a specific area cannot be known in advance. Interviewers will receive a randomly sorted list of all employers in the ZIP Code region (as described above). Interviewers will start with the first employer on the list to determine that employer’s eligibility for the survey. As mentioned above, interviewers will continue making three attempts to contact employers as they move down the list following the randomized order. They will do this until either they complete the allocation for the FLA, or the list is exhausted.
Workers
The maximum number of interviews allocated to each employer is roughly proportional to the FLA allocation. Were the allocation to be based on employer size, all interviews could be conducted at a single employer if a FLA allocation was small, and the first participating employer had a large workforce. To ensure that interviews come from more than one employer per FLA, the following schedule is used.
If the total number of interviews allocated for the FLA is:
Less than 25, the maximum number of interviews allowed per employer is five.
26-40, the maximum number of interviews allowed per employer is eight.
41-75, the maximum number of interviews allowed per employer is ten.
More than 75, the maximum number of interviews allowed per employer is twelve.
If the number of workers at an employer is less than the maximum number allowed per the criteria listed above, then all workers at the employer will be interviewed.
Most of the NAWS interviews take place on farms where there is only one group of workers. On some farms, however, workers are organized into crews consisting of several workers and a supervisor. Crew size can range from a handful of workers to more than 100, but crews of 30 workers or less are most typical based on prior years’ data. When the number of crews is large, randomly selecting workers from each crew is not feasible, and can be an imposition on the farm employer. For this reason, on farms where there are multiple crews, interviewers will first select one crew. They will then select workers to interview only from within that crew.
When a crew has to be selected from multiple crews, the crew will be selected randomly. Under some field conditions, the crew selection cannot be done using simple random sampling. In these situations, the crew will be selected using a structured approach, employing a sampling rule based on factors such as proximity or scheduling. For example, the interviewer might select the crew that is next scheduled to take a lunch break. In cases where the crew cannot be selected using simple random sampling, interviewers will record the factors that determined crew selection. As in prior years of the survey, crew selection is expected to be relatively rare.
Worker selection
When the number of workers at an establishment is greater than the maximum number that may be interviewed, interviewers follow procedures that are designed to ensure the selection of a random sample of workers. A lottery system is the preferred method.
In the case of lottery selection,
consider that lower-case
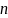 is the number of interviews allowed for an employer (e.g., 8) and
upper-case
is the number of interviews allowed for an employer (e.g., 8) and
upper-case
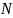 is the total number of workers available for interview (e.g., 20).
Interviewers place
is the total number of workers available for interview (e.g., 20).
Interviewers place
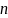 marked tags (8) and
marked tags (8) and
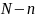 (20-8, or 12) unmarked tags in a container and shuffle them. Workers
then draw a tag and those who draw the marked tags will be
interviewed. A refusal is noted if someone who selected a marked tag
is not interviewed, e.g., because the person walked away after
getting a marked tag or stated that he/she does not wish to be
interviewed. A refusal would also be noted if a marked tag is left in
the bag after workers select tags.
(20-8, or 12) unmarked tags in a container and shuffle them. Workers
then draw a tag and those who draw the marked tags will be
interviewed. A refusal is noted if someone who selected a marked tag
is not interviewed, e.g., because the person walked away after
getting a marked tag or stated that he/she does not wish to be
interviewed. A refusal would also be noted if a marked tag is left in
the bag after workers select tags.
Though the lottery is the preferred method it is not always feasible due to the variation in crop farm labor use patterns. In cases where a lottery is impractical, interviewers use an alternate method to select workers. Interval sampling is the endorsed alternate method. For interval sampling, the interviewer identifies a random point at which to start, and then selects workers at evenly spaced intervals. In cases where workers are not visible because they are inside an object such as housing units or working inside several greenhouses, an additional method is available. The interviewer selects a random starting object and begins interviewing in the first object and proceeds through the objects in order (e.g. clockwise) until the allocation is filled. If there are more workers in an object than the remaining allocation, a raffle is conducted. Thus, the objects have a known probability of being sampled and each worker has a known probability of being sampled.
Weighting the NAWS
Survey weights should be used when analyzing NAWS data. NAWS survey weights are the product of three components:
Design weights provide each sampled worker’s probability of selection within the cycle-region stratum, including probabilities of being selected at the FLA, county, ZIP Code region, employer, and worker level.
Nonresponse adjustments correct design weights for deviations from the sampling plan, such as discrepancies in the number of interviews planned and completed in specific locations.
Post-sampling adjustments are made to each interview in order to compute unbiased population estimates from the sample data.
Data for the design weights, such as the number of crews and workers at the farm on the day of sampling, will be collected from the employer by the interviewer as part of the sampling documentation. Employer weights are calculated using information from the employer sampling frame and employer response codes recorded by interviewers. Stratum weight data will come from the FLS and QCEW. USDA CoA farm labor expenditure data is used for the county and FLA size measure. Data for post-sampling adjustments for part-time and seasonal work come from historical NAWS data.
Calculations of the nonresponse adjustments at the worker and employer level are computed simultaneously with design weights using worker sampling data as explained below; nonresponse adjustments at the cycle and region level are calculated simultaneously with cycle and region post-sampling adjustments.
Design Weights
Each worker
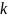 in the sample has a known probability of selection. Information
collected at each stage of sampling is used to construct the design
weights.
in the sample has a known probability of selection. Information
collected at each stage of sampling is used to construct the design
weights.
Worker
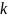 ’s
probability of selection is:
’s
probability of selection is:
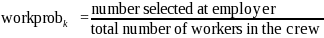
where the number selected at the employer is the minimum of either the total number of workers in the crew or the FLA allocation per employer, as described on page 10.

When interviewers encounter crop workers organized into multiple crews, they are instructed to select one crew at random. Otherwise, workers are not organized into crews. Hence, there will only ever be one selected crew, and therefore the numerator is always one.
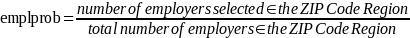
The number of employers selected includes all employers from the beginning of the randomly sorted list until the last employer where interviews were completed.

Counties are drawn sequentially from
FLAs by simple random sampling with probability proportional to size
without replacement. For example, suppose counties
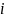 and
and
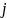 members of a selected FLA and the measure of size in county
members of a selected FLA and the measure of size in county
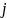 is larger than in county
is larger than in county
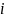 .
Probability proportional to size selection implies the probability of
drawing county
.
Probability proportional to size selection implies the probability of
drawing county
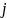 is greater than of drawing county
is greater than of drawing county
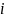 for any draw of which both counties remain eligible. Hence, when
drawing from an FLA with
for any draw of which both counties remain eligible. Hence, when
drawing from an FLA with
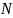 counties, the probability of drawing county
counties, the probability of drawing county
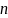 after
after
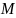 draws
is calculated as the sum of the probability it is selected at the
first draw, the probability it is selected at the second draw, the
probability it is selected at the third draw, and so on to the
probability it is selected at the
draws
is calculated as the sum of the probability it is selected at the
first draw, the probability it is selected at the second draw, the
probability it is selected at the third draw, and so on to the
probability it is selected at the
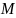 th
draw.
th
draw.
For the standard method of sampling several counties with probabilities proportional to size, without replacement, closed-form formulas for the exact inclusion probabilities do not exist. However, these probabilities can be calculated exactly using multiple summations. This procedure can be implemented in SAS within PROC IML.
Suppose the population at a particular sampling stage consists of
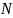 objects with sizes
objects with sizes
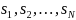 ,
having total size
,
having total size
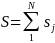 .
Let
.
Let
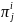 be the probability the
be the probability the
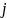 th
item is selected at the
th
item is selected at the
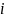 th
draw. Then for
th
draw. Then for
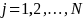 ,
,
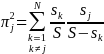
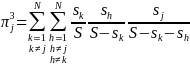
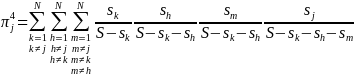 and
so on.
and
so on.
The
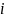 th-draw
probabilities each have the property
th-draw
probabilities each have the property
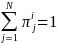 .
Finally, the probability item
.
Finally, the probability item
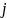 is included in a sample of size
is included in a sample of size
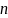 is
is
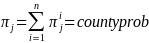 .
These inclusion probabilities have the property
.
These inclusion probabilities have the property
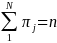 .
.
The probability FLA
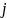 is selected within a given region is the product of the probability
FLA
is selected within a given region is the product of the probability
FLA
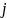 is selected for the roster,
is selected for the roster,
 ,
and the probability FLA
,
and the probability FLA
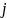 is selected for the cycle given it is on the roster,
is selected for the cycle given it is on the roster,
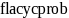 .
.
The probability FLA
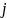 is selected from the roster can be calculated as follows:
is selected from the roster can be calculated as follows:
Suppose
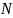 is the number of FLAs in the region,
is the number of FLAs in the region,
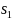 through
through
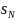 are the sizes of the FLAs,
are the sizes of the FLAs,
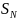 is the sum of the FLA sizes, so
is the sum of the FLA sizes, so
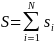 ,
and
,
and
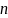 is the number of the FLAs to be selected with probabilities
proportional to size.
is the number of the FLAs to be selected with probabilities
proportional to size.
Consider a randomly ordered list of
the
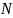 FLAs. We can construct a cumulative sum of FLA size moving down the
list such that the cumulative sum of FLA size at the
FLAs. We can construct a cumulative sum of FLA size moving down the
list such that the cumulative sum of FLA size at the
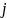 th
FLA on the list is
th
FLA on the list is
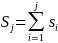 .
.
We can draw a systematic random
sample of
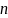 FLAs
from the list by defining
FLAs
from the list by defining
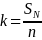 as the sampling interval and choosing a random starting point,
as the sampling interval and choosing a random starting point,
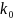 ,
between
,
between
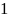 and
and
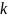 .
We then construct a list of
.
We then construct a list of
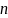 random, positive integers
random, positive integers
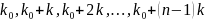 .
Hence, the
.
Hence, the
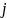 th
FLA is selected if one of these integers falls between
th
FLA is selected if one of these integers falls between
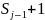 and
and
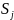 .
.
Consider the FLA appearing first in
the list. It will be selected if
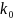 lies between 1 and
lies between 1 and
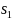 .
Thus, the probability of selecting the first FLA on the list is
.
Thus, the probability of selecting the first FLA on the list is
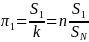 .
Therefore, the probability of selecting the
.
Therefore, the probability of selecting the
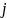 th
FLA on the list is
th
FLA on the list is
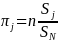 .
.
The
 is the probability that the FLA is selected in a specific cycle given
it is on the roster. The calculation is as follows:
is the probability that the FLA is selected in a specific cycle given
it is on the roster. The calculation is as follows:
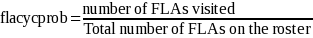
Therefore, the probability worker
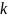 is
selected given their crew, employer, zip code, county, and FLA were
sampled in a region-cycle is the product of the sampling
probabilities at all stages of sampling,
is
selected given their crew, employer, zip code, county, and FLA were
sampled in a region-cycle is the product of the sampling
probabilities at all stages of sampling,
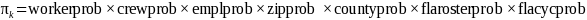
Hence, worker
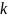 ’s
design weight,
’s
design weight,
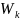 ,
is the inverse of their selection probability:
,
is the inverse of their selection probability:
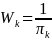 .
.
Nonresponse Adjustment
Nonresponse adjustments to the design weights account for deviations from the sampling design introduced by nonresponse. If, for example, ten interviews should have been completed at a farm but only two interviews were completed, those two interviews could be given five times the weight they would have received otherwise. Thus, each interviewee’s probability will be adjusted for deviations in the number of interviews completed at the farm. The adjusted probabilities are composite factors calculated by multiplying the worker nonresponse by the worker probability of being selected.
The response rate for workers is calculated as:

Nonresponse adjustment will also be calculated at the employer level. The region is the geographic level at which the interviews are allocated. Many of the features of the NAWS sampling were set up to overcome the lack of reliable information on seasonal employment at the county and ZIP Code level. Each cycle, there are glaring discrepancies in the number of predicted and actual eligible employers and workers at the FLA, county, and ZIP Code region level.
Given these demonstrated data issues, nonresponse adjustment at the region level will be done to account for employer nonresponse as well as nonresponse within the cycle-region stratum. This is because the region is the level at which the interviews are allocated. All other allocations are derivative, as the regional allocation is distributed across FLAs, counties and ZIP Code regions in a rolling manner. In this way, nonresponse in one area is made up for in another FLA, in order to meet the regional allocation. Additionally, by calculating a nonresponse adjustment at the region level overall, size information will, generally, be based on better quality data. This is due to the availability of more recent data and the lower likelihood of the absence or suppression of data due to privacy considerations. In addition, the region is the lowest level with enough interview coverage to adjust the weights for nonresponse because if, for some reason, there are too few interviews in a region, the region can be combined with adjacent regions for weighting purposes.
Employer nonresponse adjustment at the region level also considers ZIP Code region where no eligible employers were found. The probability of selecting the ZIP Code region within county, county within FLA, and FLA within region includes non-responding units. Adjusting at the ZIP Code region level would result in the omission of employer nonresponse in ZIP Code regions where no interviews were done. Since the sampling process allows for the possibility that there might only be one ZIP Code region selected in a FLA, the region level is the preferred level where the nonresponse adjustment can be calculated reliably.
It is important to account for the two stages of the employer selection process. First, employers are contacted and screened to determine employer eligibility. The second phase is persuading eligible employers to allow interviewers to access and interview their workers. The potential for nonresponse exists at both stages. Interviewers may be unable to contact the employer, or the employer may refuse to provide the information needed to determine employer eligibility. Eligible employers may refuse to allow access to their workers.
For the first stage in the employer selection process, we will calculate an employer screening adjustment:
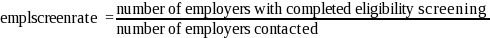
where employers with completed eligibility screening include all contacted employers where NAWS field staff are able to determine whether the employer is eligible or ineligible.
For the second stage of employer selection, the formula for the response rate among eligible employers is:
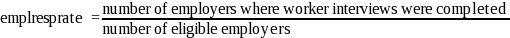
The employer adjustment calculated as the product of the screening and response rates:
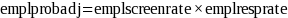
Nonresponse adjustment at the cycle-region allocation will also be calculated. The calculation of the region nonresponse adjustments will be done simultaneous with the post-sampling adjustments to take advantage of the most recent FLS data.
Post-sampling Adjustments
Post-sampling adjustments will adjust the relative value of each interview in order for national estimates to be obtained from the sample. There are five post-sampling adjustments. Two adjust for unequal probabilities of selection that can only be determined after interviews are conducted. These include the unequal probabilities of finding part-time versus full-time workers (day adjustment) and the unequal probabilities of finding seasonal versus year-round workers (seasonal adjustment). The region, cycle, and year adjustments account for the relative importance of a region’s data, a sampling cycle, and a sampling year. As discussed below, the calculation for the region adjustment will be done simultaneously with the region nonresponse adjustments. The cycle adjustment and year adjustment allow different cycles and sampling years to be combined for statistical analysis.
The region and cycle adjustments will use measures of size obtained from the FLS that are reported by quarter and region. The FLS is the only information source on levels of crop worker employment. The CoA, for instance, collects data annually rather than quarterly, and provides the desired statistic once every five years. By using FLS figures to make the size adjustment, the NAWS can adjust the weights by stratum (cycle and region) and construct unbiased population estimates. Nonresponse adjustments for size, therefore, take place at the region-within-cycle level to create corrected region weights.
The NAWS sampling plan calculates sampling allocations using FLS data collected in the year before the interviews. For example, FY 2023 data is used to plan the NAWS 2024 sample. The weights, however, will use FLS data collected during the interview year. This corrects for any discrepancies in allocations due to projecting crop worker distributions based on past years’ data.
The Day Adjustment
The day adjustment accounts for the probability of finding part-time versus full-time crop workers. Interviewers will conduct interviews during one-to-two-week visits to a specific FLA. A part-time worker, who works only two or three days per week, has a lower likelihood of being encountered than a worker employed full time. The day adjustment reflects these different probabilities of selection.
It is assumed that a worker has an equal likelihood of being sampled on each day worked. Thus, the probability of sampling a worker is related to the number of days worked by individual workers. It is therefore possible to calculate an adjustment that is simply the inverse of the number of days the worker did farm work during the week.
A respondent is always present on the day he\she was sampled. From the NAWS interview form, it can be determined how many days the respondent worked during the week. A worker who worked one day a week would have a day weight of one. A worker who worked two days per week would have a sampling probability twice that of someone working one day per week, thus a day weight of 1/2.
The day adjustment (DWTS) is computed as:

The days per week worked is reported by the crop worker. In prior surveys, almost all workers sampled worked five or six days per week. The NAWS will not sample on Sundays; therefore, workers at establishments reporting at least six workdays per week have the maximum chance of selection and the minimum day weight of one-sixth.
The few workers who do not report a number of days worked per week will receive a default value of one-sixth, the most commonly reported value.
The Season Adjustment
Correctly weighting workers is complicated by the fact that workers could, in general, be sampled several times a year. Furthermore, neither the CoA nor the FLS provides figures that can be used for the annual number of crop workers. The CoA reports the number of directly hired crop workers employed on each farm but does not adjust for the fact that some workers are employed on more than one farm in the census years. In addition, CoA crop worker counts exclude employees of farm labor contractors. Similarly, the FLS is administered quarterly and reports the number of crop workers employed each quarter, so the same worker could be reported in multiple quarters. Because of this repetition of workers across seasons, it would be invalid to derive the total number of persons working in agriculture during the year by summing quarterly figures from the FLS.
As employment information is not available for every worker for each quarter of the year, the only way to avoid double-counting of crop workers is to use the 12-month retrospective work history collected in the NAWS. Specifically, predicting future-period employment is achieved by imposing the assumption that workers who report having worked in a previous season would work in the next corresponding season. For example, a worker sampled in spring 2015 who reported working the previous summer 2014 is assumed to work in the following summer 2015. For some purposes, including the calculation of year-to-year work history changes, this assumption cannot be used. For purposes such as obtaining demographic descriptions of the worker population, however, this assumption provides satisfactory estimates.
Furthermore, it is assumed that a worker has an equal likelihood of being sampled in each season worked. Thus, the probability of sampling a worker is related to the number of seasons worked by individual workers. It is therefore possible to calculate a seasonal adjustment that is simply the inverse of the number of seasons the respondent did farm work during the previous year.
For the purposes of the NAWS, there are only three seasons per year. An interviewee always performed farm work during the trimester he\she was sampled. From the NAWS interview, it can be determined during which of the two previous trimesters the respondent also did farm work. If the interviewee only worked during the current trimester, the season weight is 1/1 or 1.00. If the interviewee worked during the current trimester and only one of the two prior trimesters, the season weight is 1/2 or 0.50. Finally, if the interviewee worked during the current and both of the prior trimesters, the season weight is 1/3 or 0.33.
This season adjustment is similar to the day adjustment in the sense that respondents who spend more time (seasons) working in agriculture have a greater chance of being sampled. Therefore, the weighting has to be inversely proportional to the number of seasons worked in order to account for the unequal sampling probability.
The Region Adjustment
The region adjustment accounts for deviations in a region’s share of completed interviews from that region’s share of allocated interviews in the sampling plan. If the number of interviews completed is smaller than the regional allocation in the sampling plan, an adjustment weight greater than one will be assigned to each interview in the region, and vice versa. These adjustments ensure that the population estimates are unbiased.
The region adjustment is based on FLS measures of regional farm employment activity. This is the best source of information available about crop workers. The FLS figures reported by region and quarter allow the weight to be sensitive to seasonal fluctuations.
Correspondence between USDA Data and the NAWS Sampling Cycles
The calculation of the region adjustment relies on two pieces of information: the FLS regional measures of size and the number of interviews completed in each region. The first step in the process of calculating the region weight is to apportion the FLS quarterly size figures among the three NAWS sampling cycles.
The USDA (FLS) figures are reported quarterly. The NAWS sampling years, however, cover non-overlapping 12-month periods (from September to August) divided into three cycles. Accordingly, it is necessary to adjust the USDA figures to fit the NAWS sampling frame by apportioning the four quarters into three cycles.
For example, the number of crop
workers in the fall cycle for a region is assumed to be the total
number of workers for that region in USDA Quarter 4 (October FLS
data) of the current fiscal year (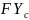 )
plus one‑third the number of workers for that region in USDA
Quarter 1 (January FLS data) of the next calendar year (
)
plus one‑third the number of workers for that region in USDA
Quarter 1 (January FLS data) of the next calendar year (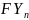 ).
The formula for the winter, spring, and summer cycles is constructed
similarly.
).
The formula for the winter, spring, and summer cycles is constructed
similarly.
Determining the NAWS Region Grouping According to Interview Coverage
The calculation of the region
adjustment (within cycle) is as follows for each region j
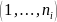 in cycle i:
in cycle i:
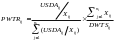 ,
,
where
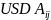 is
the USDA estimate for region
is
the USDA estimate for region
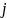 in cycle
in cycle
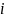 ,
,
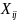 is the sum of the design weights for region
is the sum of the design weights for region
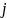 in cycle
in cycle
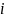 ,
,
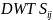 is the sum of crop worker day adjustments for region
is the sum of crop worker day adjustments for region
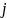 in cycle
in cycle
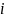 .
The day adjustment for worker
.
The day adjustment for worker
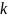 is
is
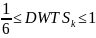 by construction so
by construction so
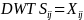 if all crop workers in region
if all crop workers in region
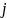 in cycle
in cycle
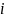 are working one day per week and
are working one day per week and
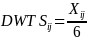 if all crop workers are working six days per week in region
if all crop workers are working six days per week in region
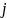 in cycle
in cycle
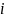 .
.
The Cycle Adjustment
NAWS data from the different sampling cycles (seasons) within the same sampling year are pooled to increase statistical power in analyses. To combine cycles, it is necessary to adjust for the number of crop workers represented in each cycle in relation to the number of interviews completed in the cycle. For instance, suppose sampling is not proportional, as explained above, but rather the same number of crop workers is interviewed in all three cycles in the fiscal year. If the USDA reported more workers for the fall and spring/summer cycles, as compared to the winter cycle, then the interviews in the fall and spring/summer would be weighted relatively more in terms of size than the interviews conducted in the winter cycle. Accordingly, the interviews in the winter would have to be down weighted in relation to the interviews in the other seasons (cycles) before the cycles could be combined.
The cycle adjustment is calculated
similarly to the region adjustment, but at the cycle-level. The sum
of the USDA size for a cycle is divided by the number of interviews
in that cycle. The calculation of the cycle adjustment is as follows
for each region
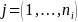 ,
cycle
,
cycle
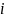 in year
in year
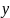 :
:
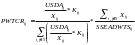
where
![]() and
and
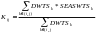
Note that
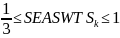 for crop worker
for crop worker
 and
and
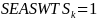 if the crop worker worked only one cycle during the year, such that
if all crop workers for region
if the crop worker worked only one cycle during the year, such that
if all crop workers for region
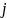 in cycle
in cycle
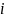 worked one day per week and only one cycle in the corresponding year,
worked one day per week and only one cycle in the corresponding year,
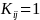 and
and
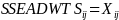 .
.
The year adjustment allows multiple sampling years to be combined for statistical analysis. It follows the same rationale as the cycle adjustment, but at the sampling-year level. If the same number of interviews are collected in each sampling year, those interviews taking place in years with more farm work activity are weighted more heavily in the combined sample.
Sampling years cannot be combined if the interviews are not comparable in terms of agricultural representation. In an extreme case, suppose that the NAWS interview budget tripled for one of the sampling years, consequently tripling the number of interviews. If the two sampling years were joined without adjustment, the larger sampling year would have an unduly large effect on the results.
To avoid this, the year adjustment
is calculated as a ratio of the total number of crop workers reported
in the USDA FLS for each sampling year to the number of interviews in
that sampling year. This is done on a cycle-by-cycle basis, but the
intent is to even out annual allocations that do not represent
similar proportions of the population. The year adjustment
calculation is as follows for each region
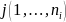 ,
cycle
,
cycle
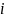 (the sum over
(the sum over
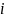 ,
,
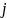 means all crop workers, all cycles, all years):
means all crop workers, all cycles, all years):
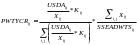
with the same notations as the preceding adjustments.
Final Weights
Final composite weights are calculated as the product of the design weights, nonresponse adjustments, and post-sampling adjustments. The cycle and year are also factored into the composite weights when multiple cycles or sampling years are used. The composite weights are scaled such that the sum of the weights is equal to the total number of interviews at the next higher level of stratification. These adjusted composite weights based on crop workers are then used for calculating the estimated proportion of workers with various attributes.
The final region weights,
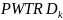 ,
are calculated at the crop worker level as follows:
,
are calculated at the crop worker level as follows:
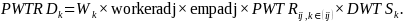
The final cycle weights,
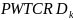 ,
including an adjustment for the length of the workweek but no
seasonal adjustment, are calculated as:
,
including an adjustment for the length of the workweek but no
seasonal adjustment, are calculated as:
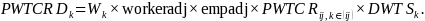
This weight may be used for the analysis of one particular year of interviews.
The final year weights, including adjustments for both the length of the workweek and season, are calculated as follows:
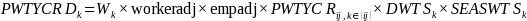
The composite weight (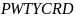 )
is used for almost all NAWS analysis. This weight allows merging
several years of analysis together. It is included in the public
access dataset.
)
is used for almost all NAWS analysis. This weight allows merging
several years of analysis together. It is included in the public
access dataset.
Statistical Reliability
Maximizing Response Rates
The NAWS response rate is the product of the employer response rate and the worker response rate times the response rates for all other levels of sampling. In FY 2023, all regions-cycle strata were used and all FLAs, counties, Zip Code regions in the sample were visited in order, the response rates for these levels of sampling are 100 percent. The employer response rate was 31 percent, and the worker response rate was 93 percent. Thus, the overall response rate was 29 percent.
In FY 2023, NAWS interviewers attempted to contact 6,074 agricultural employers, of which 61 percent were unable to be contacted or screened. Of the remaining 2,362, 30 percent were eligible to participate in the survey. A large number of potentially eligible employers have undetermined eligibility despite multiple contacts. The likelihood that an employer on the sampling list is eligible varies considerably. Many issues are responsible for the problems contacting and screening an employer. First, there is a lag in receiving employer information from BLS, so some information is out-of-date. Other sources of employer information vary in terms of completeness and the degree to which the list is vetted. At the same time, agricultural operations are not static and changes to crops, technology, or labor practices may affect the employment and timing of agricultural workers, and thus the establishment’s eligibility to participate in the survey. Also, there are businesses that are bought and sold, as well as those that start up, liquidate, or cease production. Even employers that have agricultural workers may not be eligible at all times of the year since agriculture is a seasonal industry and workers may only be needed for tasks at certain times of the year. Interviewers code the reasons for inability to screen as well as reasons for ineligibility for each selected grower.
In FY 2023, 57 percent of the randomly selected eligible employers (or their surrogates) who employed workers on the day they were contacted agreed to cooperate with the survey, and interviews were conducted at 53 percent of these eligible establishments. Considering employers for whom eligibility could not be determined, the employer response rate in FY 2023 was 31 percent using the unweighted response rate (RRU) formula from the OMB Standards and Guidelines for Statistical Surveys (2006).
Once interviewers have the employers’ agreement to cooperate with the survey, a random sample of workers is selected. In FY 2018, 93 percent of the sampled workers at eligible establishments agreed to be interviewed.
Previous NAWS data shows that item response rates are high (i.e., low nonresponse rates). Using fiscal year 2011-2016 data, the average nonresponse rate for items that do not have a skip pattern is less than 0.5 percent for each fiscal year, ranging from 0 percent to 2.4 percent. The item “When was the last time your parents did hired farm work in the U.S.A?” had the highest nonresponse rate, ranging from 1.1 in fiscal years 2014 and 2016 to 3.5 percent in FY 2011.
The average nonresponse rate for items that have a skip pattern was less than 2 percent for each fiscal year, ranging from 0 to 9.4 percent. The item “Does this employer keep in contact with you about future employment before leaving at the end of the season?” had the highest nonresponse rate, ranging from 5.1 percent in FY 2016 to 9.4 percent in FY 2013.
The NAWS is expected to have similar unit and item response rates for FY 2025.
Employer Response
To maximize employer response, the NAWS contractor will send an advance letter to agricultural employers and provide them with a brochure explaining the survey. The letter will be signed by the survey director and will include the names of the interviewers and their contact information. For further information or questions, the letter and brochure will direct employers to contact either the survey contractor at a toll-free number, or the Department of Labor’s (the Department) Contracting Officer’s Technical Representative (COTR). Employer calls will be returned quickly. In addition, the NAWS contractor will provide the COTR a list of scheduled interview trips. The list will include the counties and states where interviews will be conducted, the names of the interviewers who will be visiting the selected counties, and the dates the interviewers will be in the selected counties. The COTR will refer to the list whenever an employer calls to confirm the interviewers’ association with the survey.
Both the Department and the contractor will make presentations on the survey and will provide survey information (e.g., questionnaires) to officials and organizations that work with agricultural employers. The NAWS has received the endorsement of several employer organizations. This improves the response rate since agricultural employers sometimes call their employer organization when considering survey participation.
Before interviewers receive employer lists, NAWS office staff attempt to verify each employer’s address and contact information and conduct searches for additional addresses and phone numbers when address and phone information is missing. In addition, NAWS office staff search for physical addresses when the listed address is a post office box, law, or accounting office. Results of successful searches along with information received when advance letters are returned are incorporated in the employer contact list distributed to interviewers.
To increase employer response, interviewers are instructed to make at least three contact attempts at different times of day and on different days of the week. At least one contact is to be an in-person attempt at the employer’s address. Interviewer contact attempts are logged and monitored for compliance. Interviewers are instructed to accommodate an employer’s preference for scheduling surveys and, if needed, an interviewer can request an extension of the field period.
Intensive and frequent interviewer training are conducted to increase employer response rates. Interviewers are trained in pitching the survey in various situations and to understand the history, purpose, and use of the questionnaire. They are prepared to easily answer any question or address any concerns an employer might have. In addition, when explaining the purpose of the survey to employers, interviewers are trained to clearly distinguish the survey from enforcement efforts by the Department of Homeland Security, DOL, and other Federal agencies, and to assure employers their information is kept private and stored securely in compliance with federal information security regulations.
Worker Response
The survey’s methodology has been adapted to maximize response from this hard-to-survey population. Interviewers will pitch the survey to workers in English or Spanish, as necessary. All interviewers are bilingual. In addition, interviewers will make sure that potential respondents know that they are not associated with any enforcement agency (e.g., Immigration and Customs Enforcement). Interviewers will explain the survey to workers and obtain their informed consent verbally.
Crop workers receive a $30 honorarium to enable the survey to achieve an estimated worker response rate above 90 percent. Research indicates incentives increase response rates in social research (Ryu, Cooper, & Marans, 2006). According to the National Science Foundation, monetary incentives improve study participation and offset the costs of follow-up and recruitment of non-respondents (Zhang, 2010).
Addressing Nonresponse
Possible worker nonresponse bias
Based on previous years of NAWS data collection, the anticipated worker response rate is at least 80 percent. This level of worker response exceeds the level at which a nonresponse bias analysis is needed. However, weights include a worker nonresponse adjustment since worker nonresponse may be high within an employer.
Possible employer nonresponse bias
High rates of employer nonresponse are a concern. It is important to determine whether grower non-response is random or is due to systematic differences in characteristics of respondents and non-respondents. NAWS staff have conducted several analyses of sampling frame data and paradata to examine grower non-response. The results of these analyses did not support the need for nonresponse bias adjustment beyond what is already incorporated in the nonresponse weights.
NAWS staff will continue monitoring the effect of grower non-response using the analyses listed below. These analyses will utilize data from the NAWS sampling frame, the CoA, and the QCEW.
Assess NAWS non-response bias by comparing information in the sampling frame on eligible respondents and non-respondents. While the sampling data is somewhat sparse for non-respondents, three pieces of information are useful: geographic location, NAICS code, and the source used to obtain employer names. The NAWS uses three sources of employer names: a) the BLS UI list, b) marketing lists, and c) internet searches and contacts with knowledgeable local individuals. Geographic area and source lists are available for all employers, while NAICS codes are available for all employers who pay UI taxes, marketing list employers, and some additional employers. Employers without a NAICS code will be analyzed as a distinct group if there are enough of these employers.
Using all three variables (source, NAICS, and geography), we will make the following comparisons:
Employers allowing interviews compared to sampled employers that refused or could not be screened (i.e., excluding the ineligible),
Employers allowing interviews compared to eligible employers who refused, and
Eligible employers compared to unscreened sample members (employers whose eligibility could not be determined).
Nonresponse
bias will be calculated using the bias calculation formula from OMB’s
Standard
and Guidelines for Statistical Surveys
(2006). The formula defines bias for a particular estimate,
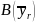 ,
as
the following:
,
as
the following:
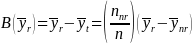
where:
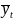 = the mean based on all sample cases.
= the mean based on all sample cases.
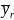 = the mean based only on respondent cases.
= the mean based only on respondent cases.
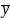 =
the mean based only on the nonresponding cases.
=
the mean based only on the nonresponding cases.
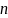 = the number of cases in the sample; and
= the number of cases in the sample; and
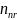 = the number of nonresponding cases
= the number of nonresponding cases
Use Markov chain analysis to incorporate information from prior data periods about growers’ states – whether eligible, ineligible, or unable to be determined – and look at the impact on response rates. A small number of agricultural employers appear on the survey’s sampling list in multiple administrations of the survey. Attempts to contact these employers may have had different outcomes at different time periods. Predicted states from the model can be used to examine possible bias.
Assess whether non-responding employers have workers with different characteristics. We compare the survey responses of workers interviewed at employers that always participate in the NAWS to the responses of workers interviewed at employers who only sometimes participate.
Possible item nonresponse bias
As discussed previously, the NAWS has item response rates that exceed 90 percent, eliminating the need for a nonresponse bias analysis for specific items. Due to the low rates of missing data, NAWS data analysis generally uses case-wise deletion. No imputations are included in the public access data.
Reliability
A probability sampling methodology will be used and estimates of the sampling errors will be calculated from the survey data.
Estimation Procedure
At the highest level of the sampling design, the region/cycle level, stratified sampling is used. Sampling is then carried out at the lower levels, independently within each stratum.
The following description is excerpted from Obenauf4:
The stratified sampling technique divides the entire population into relatively homogenous groups that are mutually exclusive and exhaustive. Samples are then drawn from each of these groups (strata) by simple random sampling or an alternate method. The entire sample is a compilation of these independent samples from each of the strata. In stratified sampling, an estimate of the population mean can be made for each of the strata.
Estimate of population mean:
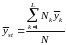 ,
,
where Nk is the population size of stratum k and L is the number of strata into which the population is divided.
If a simple random sample is taken
within each stratum (recall that other schemes can be used to draw a
sample from each of the strata), the following represents an unbiased
estimate of the variance of![]() :
:
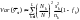 .
.
The standard error of the estimator is the square root of this estimated variance, or
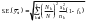 .
.
At the second stage of the sampling design, within each stratum, counties (or groups of counties) are treated as clusters (FLAs). The following description is another excerpt from Obenauf5:
The population is again divided into exhaustive, mutually exclusive subgroups and samples are taken according to this grouping. Once the population has been appropriately divided into clusters, one or more clusters are selected … to comprise the sample. There are several methods of estimating the population mean for a cluster sample. The method most pertinent to this study is that involving cluster sampling proportional to size (PPS).
With PPS sampling, the probability
(zj) that a cluster j is chosen on
a specific draw is given by
![]() ,
where Mj is the size of the jth
cluster and M is the population size. An unbiased estimate of the
population total is given by
,
where Mj is the size of the jth
cluster and M is the population size. An unbiased estimate of the
population total is given by
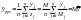 ,
,
where yj is
the sample total for y in the jth cluster, n
is the number of clusters in the sample and 2![]() represents the average of the cluster means.
represents the average of the cluster means.
To estimate the population mean, this estimate must be divided by M, the population size.
The variance of the estimator of the population total is given by,
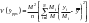
This is estimated by
![]() ,
where
,
where
![]() is the sample variance of the
is the sample variance of the
![]() values.
values.
For an estimate of the population mean,
![]() and
and
![]() .
.
In two-stage cluster sampling, the estimated variance of the estimator is then given by an iterative formula:
![]() .
.
This iterative formula is then generalized to compute the variance of the estimators in multi-stage sampling schemes with three or more levels. Exact formulas become intractable at this point, and the various statistical software packages rely upon either re-sampling methodology or linear approximations in order to estimate the variances and standard errors of the estimators.
The following is an excerpt from the SAS documentation for PROC SURVEYMEANS6.
The SURVEYMEANS procedure produces estimates of survey population means and totals from sample survey data. The procedure also produces variance estimates, confidence limits, and other descriptive statistics. When computing these estimates, the procedure takes into account the sample design used to select the survey sample. The sample design can be a complex survey sample design with stratification, clustering, and unequal weighting.
PROC SURVEYMEANS uses the Taylor expansion method to estimate sampling errors of estimators based on complex sample designs. This method obtains a linear approximation for the estimator and then uses the variance estimate for this approximation to estimate the variance of the estimate itself (Woodruff 1971, Fuller 1975)7,8.
SAS (e.g., PROC SURVEYMEANS) allows the user to specify the details of the first two stages of a complex sampling plan. In the present case, the stratification and clustering at the first two levels are specified in PROC SURVEYMEANS (strata cycle and region; cluster FLA). At the lower levels of the sampling scheme, the design attempts to mimic, as closely as is practical, simple random sampling. The software is not able to calculate exact standard errors since it presumes true simple random sampling beyond the first two levels. The sampling weights will remedy any differences in selection probabilities so that the estimators will be unbiased.
In the SURVEYMEANS procedure, the STRATA, CLUSTER, and WEIGHT statements are used to specify the variables containing the stratum identifiers, the cluster identifiers, and the variable containing the individual weights.
For the NAWS, the STRATA are defined as the cycle/region combinations used for the first level of sampling. The CLUSTER statement contains the primary sampling unit, which is the FLA.
The WEIGHT statement references a
variable that is for each observation
 ,
the product of both the sampling weight
,
the product of both the sampling weight
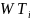 and the nonresponse weight
and the nonresponse weight
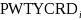 .
This variable is called
.
This variable is called
 for historic reasons. The PWT refers to a weight for the population
and thus includes the season weight, and the YCRD means that the
weight includes year, cycle, region, and day components.
for historic reasons. The PWT refers to a weight for the population
and thus includes the season weight, and the YCRD means that the
weight includes year, cycle, region, and day components.
The SURVEYMEANS procedure also allows for a finite population correction. This option is selected using the TOTAL option on the PROC statement. The TOTAL statement allows for the inclusion of the total number of PSUs in each stratum. SAS then determines the number of PSUs selected per region from the data and calculates the sampling rate. In cases such as the NAWS, where the sampling rate is different for each stratum, the TOTAL option includes a reference to a data set that contains information on all the strata and a variable _TOTAL_ that contains the total number of PSUs in each stratum.
We include here the sample code for PROC SURVEYMEANS to calculate the standard errors for our key estimator WAGET1.
proc surveymeans data=naws.crtdvars total=naws.regioninfo;
strata region12 cycle;
cluster FLA;
var waget1;
weight pwtycrd;
Precision of Key Estimators
The NAWS is primarily a surveillance survey that provides descriptive statistics about the United States crop worker population. Periodic reports posted to the website and presentations at conferences and stakeholder meetings are used to disseminate the survey results. In addition, the data are used by researchers, policy analysts and service program staff primarily for program planning and policy analysis. Two key variables of interest to these groups are FWRDAYS, which is the number of days worked per year by a respondent, and WAGET1, which is the average hourly wage of a respondent. Based on data collected in fiscal years 2019-2022, a combined sample size of 4,770 respondents, using the NAWS current weights, the 2-standard-error confidence interval for FWRDAYS was 215 days ± 9.2 days. That is, with approximately 95 percent confidence, the average number of days annually worked, per person, lies between 206 and 224 days.9 This constitutes a margin of error of ±4.3 percent of the estimated value.
For average wage (WAGET1), the 2-standard-error confidence interval was $14.07 ± 0.27. With approximately 95 percent confidence, the average wage lies between $13.80 and $14.34. This yields a margin of error of ±1.9 percent of the estimated value.
There are numerous other variables of interest, whose standard errors vary greatly. These two are offered as examples that show some of the range of possible precisions obtained.
Tests
This submission seeks to:
Include H-2A crop workers in the NAWS sample;
Add questions on heat-related illness, prevention, and training;
Add questions on foodborne illness, prevention, and training;
Add questions on precision agriculture;
Add a question on controlled environmental agriculture;
Add a question on hours worked for wages in the week prior to the interview;
Reinstate a question on union membership; and
Combine the race and ethnicity questions.
Burden associated with the proposed questions will be offset by the discontinuance of supplemental questions on access to healthcare.
ETA commissioned a study to assess the feasibility of including H-2A crop workers in the survey. The study found that including H-2A respondents could address increasing stakeholder demand for information on this population without threatening the reliability and efficiency of existing NAWS data collection methods.
ETA developed the new questions on heat illness, foodborne illness, precision agriculture, and covered agriculture in consultation with SMEs in government and the private sector. After developing draft questions, ETA’s contractor performed four two-hour focus groups with crop workers, two each in Salinas, CA and Hidalgo, TX consisting of separate groups of 10 men and 10 women. In total, forty crop workers - 20 men and 20 women - participated in the focus groups. Each group discussed questions in the proposed domains, which allowed the contractor to ascertain worker experience and knowledge related to the new domains and obtain feedback on question language and content. Draft questions were revised based on analysis of focus group data, with particular attention to balancing data collection needs and respondent burden.
After finalizing draft questions with Federal agency partners and SMEs, ETA's contractor conducted individual cognitive interviews, each lasting two hours, with eight crop workers. The purpose of the cognitive interviews was to assess whether crop workers comprehended the questions and response items, and to ensure they interpreted them consistently. The new questions uploaded with this ICR incorporate revisions identified in the cognitive interviews.
Most NAWS questions have been administered for 36 years, are well understood, and provide high quality data.
Statistical Consultation
In the last two years, the following individuals have been consulted on statistical aspects of the survey design:
Stephen Reder, Robert Fountain, and Yves Labissiere, Professors, Portland State University, (503) 725-3999, (503) 725-5204, and (503) 725-8078, respectively.
The data will be collected under contract to JBS International, Inc. (650) 373-4900. Analyses of the data will be conducted by Daniel Carroll, ETA (202) 693-2795, Emily Finchum, ETA (202) 693-3647, and JBS International, Inc.
REFERENCES
Fuller, W.A. (1975). Regression Analysis for Sample Survey, Sankhyā, 37, Series C, Pt. 3, 117-132.
Obenauf, W. (2003). An Application of Sampling Theory to a Large Federal Survey. Portland State University, Department of Mathematics and Statistics. 2003.
Ryu, E., Couper, M, & Marans, R. (2006) Survey incentives: Cash vs. in-kind; Face-to-face vs. mail; Response rate vs. nonresponse error. International Journal of Public Opinion Research, 18 (1): 89-106.
SAS Institute Inc., SAS/STAT® User’s Guide, Version 8, Cary, NC: SAS Institute Inc., 1999, 61, 3.
Woodruff, R. S. (1971). A Simple Method for Approximating the Variance of a Complicated Estimate, Journal of the American Statistical Association, 66, 411–414.
Zhang, F. (2010). Incentive experiments: NSF experiences. (Working Paper SRS 11-200). Arlington, VA: National Science Foundation, Division of Science Resources Statistics.
1 “Crop worker” accurately describes members of the population of interest. We do not use “farm worker” or “farmworkers” as these are broad terms that encompass persons outside the population of interest.
2 The number of unique FLAs visited may be less than 106, as some FLAs are sampled each cycle.
3 The 2022 CoA reports the number of direct-hire farms. See Table 75, Summary by North American Industry Classification System: 2022, Hired farm labor, farms. Collectively 256,373 farms directly hired workers in NAICS 1111 (Oilseed and grain farming), 1112 (Vegetable and melon farming), 1113 (Fruit and tree nut farming), 1114 (Greenhouse, nursery, and floriculture production), and 1119 (Other crop farming). The QCEW reports the number of NAICS 1151 establishments: www.bls.gov/cew/data.htm.
4 Obenauf, W. (2003), “An Application of Sampling Theory to a Large Federal Survey”, Portland State University Department of Mathematics and Statistics.
5 Obenauf, W. (2003), “An Application of Sampling Theory to a Large Federal Survey”, Portland State University Department of Mathematics and Statistics.
6 SAS Institute Inc., SAS/STAT® User’s Guide, Version 8, Cary, NC: SAS Institute Inc., 1999, 61, 3.
7 Woodruff, R. S. (1971). A Simple Method for Approximating the Variance of a Complicated Estimate, Journal of the American Statistical Association, 66, 411–414.
8 Fuller, W. A. (1975). Regression Analysis for Sample Survey, Sankhyā, 37, Series C, Pt. 3, 117–132.
9 The resulting confidence interval of 205.8 to 224.2 is rounded to 206 to 224.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | 1205-0453: NAWS Supporting Statement Part B |
| Author | carroll.daniel.j |
| File Modified | 0000-00-00 |
| File Created | 2024-12-27 |
© 2026 OMB.report | Privacy Policy
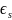 )
)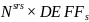 )
)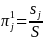 ,
,