Supporting Statement B - 1205-0448 - April 2014
Supporting Statement B - 1205-0448 - April 2014.docx
Employment and Training Data Validation Requirement
OMB: 1205-0448
SUPPORTING STATEMENT FOR REQUEST FOR OMB APPROVAL
UNDER THE PAPERWORK REDUCTION ACT
PART B –
COLLECTION OF INFORMATION EMPLOYING STATISTICAL METHODS
1. Description of Universe and Selection Methods Used
As described in Part A of the Supporting Statement, the data validation methodology consists of two parts:
1) Report validation evaluates the validity of aggregate reports submitted to ETA by
53 states and territories. It does so by checking the accuracy of the state’s reporting software, which is used to calculate the reports. The universe for report validation comprises all participant records included in the extract file. Report validation is accomplished by independently processing the entire extract file of participant records, providing validation counts, and comparing the validation counts to those reported by the state or grantee.
Data element validation assesses the accuracy of participant data records. For Workforce Investment Act (WIA) Title IB, the universe for data element validation comprises records of participants who exited between April 1st of the year prior to the program year through March 31st of the current program year. The universe for WIA programs is detailed in Table I-2 of the Workforce Investment Act Standardized Record Data (WIASRD) data book located at the following link http://www.doleta.gov/Performance/results/Reports.cfm?#wiasrd_databook. For Wagner-Peyser, the universe for data element validation is comprised of participants who have been placed and retained in employment. Currently, this information is collected at the national-level and may vary considerably year to year as the entered employment rate fluctuates. For Trade Adjustment Assistance (TAA), the universe for data element validation comprises all Trade Act participant records submitted to ETA during the prior fiscal year. Detailed breakouts by state are available at http://www.doleta.gov/tradeact/TAPR_2010.cfm. For the National Farmworker Jobs Program (NFJP) and Senior Community Service Employment Program (SCSEP), the universe for data element validation comprises all NFJP and SCSEP records submitted to ETA during the prior program year. This information is drawn from national case management software and is not uploaded at the state-level. The universe from which the data is obtained for these programs is described in the People Served by Program report available at http://www.doleta.gov/Performance/results/quarterly_report/June_30_2010/WSR_June_30_2010.pdf#page=6. Data element validation is performed by reviewing samples of participant records against source documentation to ensure compliance with federal definitions and to verify the accuracy of the information contained in the states extract file.
The data validation process results in an estimate of the error rates for each data element and each reported count. Error rates are estimated separately for each state or grantee for the WIA, Wagner-Peyser, TAA, NFJP and SCSEP programs. Data element validation error rates cannot be estimated for Wagner-Peyser because statistically valid samples are not used due to the large number of participants in the Wagner-Peyser program.
The methodology for data element validation employs sampling to improve the efficiency of the validation process. To minimize states’ and grantees’ burden in performing validation consistent with producing a reliable estimate of the error rates, the data element validation process is designed to compute a reliable error rate using the smallest possible sample size. To accomplish these objectives, three sampling techniques are used:
Variable sampling rates among states are used to reduce the burden on small states and grantees as much as possible.
Oversampling high-risk and high-importance cases is used to provide a more accurate estimate of the error rate.
For WIA Title IB and TAA programs, multistage sampling is employed in an effort to minimize burden. Samples of offices are selected, and records are selected for validation only within sampled offices. This multistage design reduces the number of locations that state staff must visit to access supporting documentation.
These sampling methods balance the numbers of records and the numbers of locations so that the overall burden is reduced as much as possible, while still achieving a reliable estimate of error. See the Methodology Details documentation included in the package for more specific details.
To reduce the burden on states and grantees, ETA provides validation software that calculates the validation values, imports the reported counts, draws the data element validation samples, produces online and paper validation worksheets, calculates error rates, and produces the validation reports.
Data validation relies on existing records from state and grantee management information systems and case files. Response rates are not an issue with the data validation process because the data are sampled from the entire participant file and so do not require survey responses.
2. Procedures for the Collection of Information
A. Statistical Methodology for Stratification and Sample Selection
Item B.1 above indicates that report validation does not require states to obtain information via surveys because the entire participant file is utilized during this validation procedure.
For data element validation, multistage samples of participant records are drawn. Independent samples are selected in each state for 8 groups – TAA, NFJP, SCSEP and 5 WIA groups (dislocated workers, NEGs, adults, older youth, and younger youth). For NFJP and SCSEP, stratification is not employed within the samples either in the selection of offices or records. For WIA and TAA, stratification of offices is employed to reduce the burden of validation.
For WIA title IB programs, offices are selected at the first stage for the data element validation. Each office is assigned a weight equal to the sum of the weights for the individual records associated with that office. For each state’s WIA validation, offices are stratified. Up to 5 strata may be created. The strata are based upon the number of offices in the state, the weight of each office, and the distribution of records across the 5 WIA groups. Up to 15 offices may be selected per stratum, leading to a maximum of 75 offices sampled for the state.
For TAA programs, offices are selected at the first stage for the data element validation. Each office is assigned a weight equal to the sum of weights for the individual records associated with that office. For each state’s TAA validation, a sample of offices is then selected using probability proportional to size (PPS) methods. The selection probability of an office is based upon the total number of offices in the state and the weight of that office. Samples of records are then drawn from within the selected offices. Each record has a probability of selection proportional to its weight. The expected number of offices selected in a state is based on the total number of offices shown in Table A. For NFJP and SCSEP, no offices are sampled. Records are sampled directly. Each record has a probability of selection proportional to its weight.
To increase the efficiency of the process, records receive a risk weight of 1, 2, or 3 based upon two factors: whether the record is a success for calculating performance (i.e., whether the adult, dislocated worker, NEG, older youth, TAA, NFJP, or SCSEP participant was employed in the first quarter after exit or the younger youth received a diploma within one quarter after exit), and the risk that the data used to calculate performance are in error.
In addition, WIA records receive a density weight that equals the number of elements to be validated per record. The two weights are added to determine a composite weight. The composite weights result in oversampling records that are more likely to contain errors and are judged to be more substantively important (i.e., an error in such a record would be more important for a state or grantee).
1. WIA Title IB and TAA Methodological Details
Determine Sample Date Range
Determine the start and end date ranges for the Sampling Cohort for the selected report. The Sample Start Date and Sample End Date for the sampling cohort are equal to the start and end date for the Retention Rate calculations.
Determine the Sample Frame and Sample Size
a. Determine the number of records (NFS) in each funding stream
NFS = Count of records where Funding Stream = FS and Date of Exit >= Sample Start Date and Date of Exit <= Sample End Date and [(More Than Self-Services = 1 and (FS = Adult or DW or NEG)] or (Older Youth or Younger Youth) or (TAA).
Note: Whenever the specification refers to records, it always refers to those who satisfy the above conditions.
b. Calculate the sample size for each funding stream (n_samplefs) using the equation below.
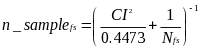
Where n_samplefs = sample size of the funding stream, Nfs = number of records in the funding stream and CI = 95% half-width of the confidence interval.
If Nfs >= 500, then CI = 0.035, Else CI = 0.04
If n_samplefs > 350 then set n_samplefs = 350
c. Set values for STATEMIN (the minimum number of PSUs to select for the state) and MIN_STR (the minimum number of PSUs to select for a stratum/funding stream)
Set STATEMIN = 15
Set MIN_STR = 10
Assigning Weights to Each Record
Each record in the sample frame must be assigned three weights. The first weight is the risk weight. This weighting is a function of a few key elements. The equations used to calculate the risk weight for adults, dislocated workers, NEGs, and older youth are the same. A different set of equations is used to calculate the younger youth risk weight. The second weight is the density weight, which provides information about the number of elements in each record that states will validate. The equations used to calculate the density weight will differ by funding stream. Third, the composite weight aggregates the risk and the density weights by summing them. For the purpose of the sampling of PSUs and records, the software will be using the composite weight.
Records that meet the criteria for more than one funding stream must be considered independently for each funding stream. In other words, a record that is in funding stream A and D must be treated as two separate records – one with a funding stream = A and another with a funding stream = D – with separate weights.
Risk Weighting
For Adults, Dislocated Workers, NEGs, and Older Youth, the risk weight is calculated based upon the values in Employment in the 1st quarter after the exit quarter and the type of employment match for the 1st, 2nd, and 3rd quarters after the exit.
Note: the subscript j is used to denote the specific records. For example, if there are 250 records, each record will be numbered 1 to 250. Record(j) = 10 refers to the 10th record.
a. If EMPLOYMENT IN THE FIRST QTR AFTER THE EXIT QTR = 2 then Set R_Weight_Emp(j) = 1
b. If EMPLOYMENT IN THE FIRST QTR AFTER THE EXIT QTR = 1 and TYPE OF EMPLOYMENT MATCH 1ST QUARTER AFTER EXIT QUARTER <> 5 and TYPE OF EMPLOYMENT MATCH 2ND QUARTER AFTER EXIT QUARTER <> 5 and TYPE OF EMPLOYMENT MATCH 3RD QUARTER AFTER EXIT QUARTER <> 5, then Set R_Weight_Emp(j) = 2
c. If EMPLOYMENT IN THE FIRST QTR AFTER THE EXIT QTR = 1 and (TYPE OF EMPLOYMENT MATCH 1ST QUARTER AFTER EXIT QUARTER = 5 or TYPE OF EMPLOYMENT MATCH 2ND QUARTER AFTER EXIT QUARTER = 5 or TYPE OF EMPLOYMENT MATCH 3RD QUARTER AFTER EXIT QUARTER = 5) then Set R_Weight_Emp(j) = 3
For Younger Youth, the risk weight is calculated based upon the School Status at Participation, Date Attained Degree or Certificate, Exit Date, and Attained, Diploma, GED, or Certificate fields.
a. If (SCHOOL STATUS AT PARTICIPATION = 3 or SCHOOL STATUS AT PARTICIPATION = 5) then Set R_Weight_YY(j) = 1
b. If (SCHOOL STATUS AT PARTICIPATION = 1 or SCHOOL STATUS AT PARTICIPATION = 2 or SCHOOL STATUS AT PARTICIPATION = 4) and (DATE ATTAINED DEGREE OR CERTIFICATE is null or (DATE ATTAINED DEGREE OR CERTIFICATE < DATE OF PARTICIPATION) or (DATE ATTAINED DEGREE OR CERTIFICATE > End of Quarter after the Exit Quarter)) then Set R_Weight_YY(j) = 2
c. If (SCHOOL STATUS AT PARTICIPATION = 1 or SCHOOL STATUS AT PARTICIPATION = 2 or SCHOOL STATUS AT PARTICIPATION = 4) and (ATTAINED DIPLOMA, GED, OR CERTIFICATE = 1 or ATTAINED DIPLOMA, GED, OR CERTIFICATE = 2) and DATE ATTAINED DEGREE OR CERTIFICATE <= End of Quarter after the Exit Quarter and DATE ATTAINED DEGREE OR CERTIFICATE and DATE ATTAINED DEGREE OR CERTIFICATE >= DATE OF PARTICIPATION, then Set R_Weight_YY(j) = 3
Density Weighting
In addition to weighting the records for risk, they must have a weight for density. The density weight measures the number of elements in the record that will be validated for the appropriate funding stream. (The specifics will be provided with the list of elements for validation.) For records that are in multiple funding stream, the software must assign separate weights for each funding stream.
D_weightFS(j) = Count of data elements that that are on the list of validated elements for the appropriate funding stream that have a positive value; j refers to the specific record.
Composite Weighting
The risk and density weighting must be consolidated into a composite weight so that the software can use the weights in the rest of the specification. The composite weight is equal to the sum of the risk and the density weight. The software must assign the composite weight to each record in the sample frame for each funding stream that record is part of.
C_weightFS(j) = D_weightFS(j) + R_Weight_Emp(j)
C_weightY(j) = D_weightY(j) + R_Weight_YY(j) (for younger youth)
Note: in the remainder of the specification, when we refer to weights, we are referring to the composite weight.
Determining the PSUs
The software must allow users to select PSUs by selecting from three options: record, office, and WIB. If the user selects the record option, then the software can skip the clustering instructions. On the other hand, if the user selects office or WIB, then the software must determine if the data contain the information needed to identify the PSUs. If there are not enough PSUs, then the software must notify the user and use records as the default PSU.
Please Note: the subscript i is used to denote the specific PSUs. For example, if there are 50 PSUs, each will be numbered 1 to 50. PSU(i) = 10 refers to the 10th PSU.
Identifying the PSUs
When users select the sample option, the software needs to ask if the user wants the software to sample by record, by office, or by WIB. Set PSUType = whichever the user selected – record, office, or WIB If PSUType = Record, then set STRATUM = A and STR_A(i) = Certainty for all i offices and go to step Sampling Records. If PSUType = Office, then count the number of unique values in the Office Name field (TOTPSU) that contain records where Date of Exit >= Sample Start Date and Date of Exit <= Sample End Date.
If TOTPSU > STATEMIN, then skip to Stratification. If TOTPSU <= STATEMIN, then provide the user with a message saying “There are fewer than the minimum number of offices required for clustering. The software will not be able to cluster the sample.” Then set PSUType = Record and set STRATUM = A and STR_A(i) = Certainty for all offices and go to step Sampling Records.
If PSUType = WIB, then count the number of unique values in the WIB Name field (TOTPSU) that contain records where Date of Exit >= Sample Start Date and Date of Exit <= Sample End Date.
If TOTPSU > STATEMIN, then skip to Stratification. If TOTPSU <= STATEMIN, then provide the user with a message saying “There are fewer than the minimum number of WIBs required for clustering. The software will not be able to cluster the sample.” Then set PSUType = Record and set STRATUM = A and STR_A(i) = Certainty for all WIBs and go to Sampling Records.
Stratification
For the software to be able to select a set of PSUs for all five funding streams, it must look at the distribution of weights across all PSUs, by PSU, and by funding stream. If these distributions meet certain criteria, then the software can directly sample PSUs. The distributions do not meet those criteria, then the software must create strata of PSUs and select PSUs to assign to this strata.
Initial Calculations
Below are a set of numbers that the software must calculate and store for future use. These numbers may be used to create strata and to calculate weights that are needed to calculate error rates for the summary and analytical report.
a. For each PSU, the software must calculate a weight `for each funding stream and a total weight. MOSFS(i) is the total weight of records that are in funding stream FS for the PSU i. FS = A, D, N, O, or Y represent adult, dislocated worker, NEGs, older youth, and younger youth, where i refers to the particular PSU. MOSTOT(i) represents the total weight of all the records in PSU i. Records in multiple funding streams are included multiple times, once for each funding stream.
MOSA(i) = C_weightA(j) for each adult record in the PSU
MOSD(i) = C_weightD(j) for each dislocated worker record in the PSU
MOSN(i) = C_weightN(j) for each NEG record in the PSU
MOSO(i) = C_weightO(j) for each older youth record in the PSU
MOSY(i) = C_weightY(j) for each younger youth record in the PSU
MOSTOT(i) = MOSA(i) + MOSD(i) + MOSN(i) + MOSO(i) + MOSY(i) for each PSU
b. Count the number of PSUs that contain each funding stream (N_PSUFS)
N_PSUA = Count of PSUs where MOSA(i) > 0
N_PSUD = Count of PSUs where MOSD(i) > 0
N_PSUN = Count of PSUs where MOSN(i) > 0
N_PSUO = Count of PSUs where MOSO(i) > 0
N_PSUY = Count of PSUs where MOSY(i) > 0
c. Calculate the proportion of the weight contained in PSUs that have funding stream FS as function of the total weight for all funding streams (P_STRFS)
P_STRA = MOSTOT(i) for each PSU where MOSA(i) > 0 / MOSTOT(i) for all PSUs
P_STRD = MOSTOT(i) for each PSU where MOSD(i) > 0 / MOSTOT(i) for all PSUs
P_STRN = MOSTOT(i) for each PSU where MOSN(i) > 0 / MOSTOT(i) for all PSUs
P_STRO = MOSTOT(i) for each PSU where MOSO(i) > 0 / MOSTOT(i) for all PSUs
P_STRY = MOSTOT(i) for each PSU where MOSY(i) > 0 / MOSTOT(i) for all PSUs
est: P_STRFS >= 1 and P_STRFS <=5
Stage 1 Stratification
Once the software has calculated the above values, it must determine if strata need to be created or if direct sampling of PSUs can occur. This is accomplished by calculating the expected number of PSUs that would contain each funding stream if the software sampled PSUs without creating strata.
a. Calculate the expected number of PSUs per Funding Stream (EXP_STR1FS). This is a function of the proportion of the weight for the funding stream times the minimum number of PSUs to sample.
EXP_STR1A = P_STRA * STATEMIN
EXP_STR1D = P_STRD * STATEMIN
EXP_STR1N = P_STRN * STATEMIN
EXP_STR1O = P_STRO * STATEMIN
EXP_STR1Y = P_STRY * STATEMIN
b. Identify the smallest of the expected number of PSUs and its associated funding stream. If the smallest of the expected number of PSUs is greater than or equal to the stratum minimum for the funding stream (MIN_STR), there is no need to create multiple strata. On the other hand, if it is less than the stratum minimum, create two strata, stratum A and stratum B. Stratum A contains the PSUs containing the minimum funding stream, and the Stratum B contains the remaining PSUs (i.e. it contains all PSUs that do not contain any records in the minimum funding stream). Then, determine how many PSUs to select from Stratum A: either MIN_STR or all PSUs in Stratum A.
Set STR_TESTA = Minimum of (EXP_STR1A, EXP_STR_1D, EXP_STR1N, EXP_STR1O EXP_STR1Y) for all Funding Streams where EXP_STR1 > 0
Note: If two or more expected values equal the minimum, the software should use the following order when deciding which funding stream is the minimum: Older Youth, Younger Youth, NEGs, Dislocated Worker, Adults.
Set MINFS_A = the funding stream that has the minimum expected number of PSUs (A, D, N, O, or Y). If STR_TESTA >= MIN_STR then STRATUM_NUM = 1 and n_Sel_A = STATEMIN and set STRATUM = A for every PSU and go to Select PSUs. STRATUM_NUM counts the number of strata created. n_Sel_A provides the number of PSUs in stratum A. It is a specific version of a more general variable n_Sel_S where S can be A, B, C, D, and E for each of the potential stratum. If STR_TESTA < MIN_STR then Set STRATUM = A for every PSU where MOSMINFS_A > 0, Else Set STRATUM = B.
c. Determine the number of PSUs to select from Stratum A by looking at the number of PSUs that contain records in MINFS_A funding stream. n_Sel_A is the number of PSUs sampled from stratum A. If N_PSUMINFS_A >= MIN_STR, then set n_Sel_A = MIN_STR, else n_Sel_A = N_PSUMINFS_A.
Stage 2 Stratification
This section of the specification determines if the software needs to create a stratum C. The method used for this determination is the same as Stage 1 Stratification, except we have removed at least one funding stream from consideration and we must account for the PSUs in the first strata.
a. Determine the expected number of PSUs that contain each funding stream that will be sampled from stratum A. (EXP_STR2_A FS )
If N_ PSUMINFS_A <= MIN_STR then EXP_STR2_A FS = Count of PSUs where MOSFS(i) > 0 and STRATUM = A for each funding stream, calculate the expected value for Stratum B (EXP_STR2_B FS )].
If N_ PSUMINFS_A > MIN_STR calculate the proportion of the weight contained in PSUs that have funding stream FS as function of the total weight for all funding streams for stratum A (P_STR_AFS). Repeat this for each funding stream:
P_STR_AA = MOSTOT(i) for each PSU where MOSA(i) > 0 and STRATUM = A / MOSTOT(i) for all PSUs where STRATUM = A
P_STR_AD = MOSTOT(i) for each PSU where MOSD(i) > 0 and STRATUM = A / MOSTOT(i) for all PSUs where STRATUM = A
P_STR_AN = MOSTOT(i) for each PSU where MOSN(i) > 0 and STRATUM = A / MOSTOT(i) for all PSUs where STRATUM = A
P_STR_AO = MOSTOT(i) for each PSU where MOSO(i) > 0 and STRATUM = A / MOSTOT(i) for all PSUs where STRATUM = A
P_STR_AY = MOSTOT(i) for each PSU where MOSY(i) > 0 and STRATUM = A / MOSTOT(i) for all PSUs where STRATUM = A
For each funding stream calculate the expected value for Stratum A (EXP_STR2_A FS )
EXP_STR2_A FS = P_STR_AFS * n_SEL_A
EXP_STR2_A MINFS_A should equal n_SEL_A
b. Calculate the expected value for Stratum B (EXP_STR2_B FS ).
Calculate the proportion of the weights of each funding stream in PSUs where Stratum = B (P_STR1_BFS).
P_STR1_BA = MOSTOT(i) for each PSU where MOSA(i) > 0 and STRATUM = B / MOSTOT(i) for all PSUs where STRATUM = B
P_STR1_BD = MOSTOT(i) for each PSU where MOSD(i) > 0 and STRATUM = B / MOSTOT(i) for all PSUs where STRATUM = B
P_STR1_BN = MOSTOT(i) for each PSU where MOSN(i) > 0 and STRATUM = B / MOSTOT(i) for all PSUs where STRATUM = B
P_STR1_BO = MOSTOT(i) for each PSU where MOSO(i) > 0 and STRATUM = B / MOSTOT(i) for all PSUs where STRATUM = B
P_STR1_BY = MOSTOT(i) for each PSU where MOSY(i) > 0 and STRATUM = B / MOSTOT(i) for all PSUs where STRATUM = B
For each funding stream calculate the expected value for Stratum B (EXP_STR2_B FS )
EXP_STR2_B FS = P_STR1_BFS * (STATEMIN - n_SEL_A)
EXP_STR2_B MINFS_A should equal 0
c. Calculate the expected value for each funding stream (EXP_STR2 FS ) by summing the expected value for the funding stream in each stratum.
EXP_STR2 FS = EXP_STR2_A FS + EXP_STR2_B FS
d. Determine the smallest of the expected number of PSUs
Set STR_TESTB = Minimum of (EXP_STR2 FS) for all funding streams where P_STR1_BFS > 0. If two or more expected values equal the minimum, the software should use the following order when deciding which funding stream is the minimum: Older Youth, Younger Youth, NEGs, Dislocated Worker, and Adults. Set MINFS_B = the funding stream that has the minimum expected number of PSUs identified in 1 above, the funding stream associated with STR_TESTB (subject to the note).
If STR_TESTB >= MIN_STR then n_Sel_B = Maximum of (MIN_STR or (STATEMIN - n_Sel_A)) and STRATUM_NUM = 2 and go to Select PSUs. If STR_TESTB < MIN_STR then Set STRATUM = C for every PSU where MOSMINFS_B = 0 and STRATUM <> A.
e. Determine the number of PSUs to select from Stratum B
Count the number of PSUs in Stratum B (N_STR_B)
N_STR_B = Count of PSUs where STRATUM = B. If N_STR_B >= (MIN_STR - EXP_STR2_AMINFS_B) then set n_Sel_B = (MIN_STR - EXP_STR2_AMINFS_B), else n_Sel_B = N_STR_B.
Stage 3 Stratification
This section of the specification repeats the procedure for Stage 2 stratification to determine if the software needs to create stratum C.
a. Calculate the expected value for Stratum B (EXP_STR3_B FS )
If n_Sel_B = N_STR_B then EXP_STR3_B FS = Count of PSU where MOSFS(i) > 0 and STRATUM = B go to b. If N_STR_B > N_Sel_B, then calculate the proportion of the weights of each funding stream where Stratum = B (P_STR2_BFS)
P_STR2_BA = MOSTOT(i) for each PSU where MOSA(i) > 0 and STRATUM = B / MOSTOT(i) for all PSUs where STRATUM = B
P_STR2_B D = MOSTOT(i) for each PSU where MOSD(i) > 0 and STRATUM = B / MOSTOT(i) for all PSUs where STRATUM = B
P_STR2_BN = MOSTOT(i) for each PSU where MOSN(i) > 0 and STRATUM = B / MOSTOT(i) for all PSUs where STRATUM = B
P_STR2_BO = MOSTOT(i) for each PSU where MOSO(i) > 0 and STRATUM = B / MOSTOTIi) for all PSUs where STRATUM = B
P_STR2_BY = MOSTOT(i) for each PSU where MOSY(i) > 0 and STRATUM = B /
MOSTOT(i) for all PSUs where STRATUM = B
For each funding stream calculate the expected value for Stratum B (EXP_STR3_B FS )
EXP_STR3_B FS = P_STR2_BFS * n_SEL_B
EXP_STR3_B MINFS_B should equal n_SEL_B
b. Calculate the expected value for Stratum C (EXP_STR3_C FS )
Calculate the proportion of the weights of each funding stream where Stratum = C (P_STR1_CFS )
P_STR1_CA = MOSTOT(i) for each PSU where MOSA(i) > 0 and STRATUM = C / MOSTOT(i) for all PSUs where STRATUM = C
P_STR1_C D = MOSTOT(i) for each PSU where MOSD(i) > 0 and STRATUM = C / MOSTOT(i) for all PSUs where STRATUM = C
P_STR1_C N = MOSTOT(i) for each PSU where MOSN(i) > 0 and STRATUM = C / MOSTOT(i) for all PSUs where STRATUM = C
P_STR1_C O = MOSTOT(i) for each PSU where MOSO(i) > 0 and STRATUM = C / MOSTOT(i) for all PSUs where STRATUM = C
P_STR1_C Y = MOSTOT(i) for each PSU where MOSY(i) > 0 and STRATUM = C / MOSTOT(i) for all PSUs where STRATUM = C
For each funding stream calculate the expected value for Stratum C (EXP_STR3_C FS )
EXP_STR3_C FS = P_STR1_CFS * Max(0,(STATEMIN-(n_SEL_A + n_SEL_B)))
EXP_STR3_C MINFS_A and EXP_STR3_C MINFS_B should equal zero.
c. Calculate the expected value for each funding stream (EXP_STR3FS )
EXP_STR3FS = EXP_STR2_AFS + EXP_STR3_BFS + EXP_STR3_CFS
d. Determine the smallest of the expected number of PSUs
Set STR_TESTC = Minimum of (EXP_STR3FS) for all funding streams where P_STR1_CFS > 0
Note: If two or more expected values equal the minimum, the software should use the following order when deciding which funding stream is the minimum: Older Youth, Younger Youth, NEGs, Dislocated Worker, Adults.
Set MINFS_C = the funding stream that has the minimum expected number of PSUs identified in a above. If STR_TESTC >= MIN_STR then n_Sel_C = Maximum of (MIN_STR, (STATEMIN – (n_Sel_A n_Sel_B)) and STRATUM_NUM = 3 and go to Select PSUs. If STR_TESTC < MIN_STR then Set STRATUM = D for every PSU where MOSMINFS_C = 0 and STRATUM <> A and STRATUM <> B
e. Determine the number of PSUs to select from Stratum C
Count the number of PSUs in Stratum C (N_STR_C)
N_STR_C = Count of PSUs where STRATUM = C
If N_STR_C >= (MIN_STR – (EXP_STR2_AMINFS_C + EXP_STR3_B MINFS_C)) then set n_Sel_C = (MIN_STR - (EXP_STR2_AMINFS_C + EXP_STR3_B MINFS_C)), else n_Sel_C = N_STR_C.
Stage 4 Stratification
This section of the specification repeats the procedure for Stage 3 stratification to determine if the software needs to create stratum E.
a. Calculate the expected value for Stratum C (EXP_STR4_C FS )
If n_Sel_C = N_STR_C then EXP_STR4_C FS = Count of PSU where MOSFS(i) > 0 and STRATUM = C go to calculate the expected value for Stratum D (EXP_STR4_DFS )
Calculate the proportion of the weights of each funding stream in Stratum C (P_STR2_CFS)
P_STR2_CA = MOSTOT(i) for each PSU where MOSA(i) > 0 and STRATUM = C / MOSTOT(i) for all PSUs where STRATUM = C
P_STR2_CD = MOSTOT(i) for each PSU where MOSD(i) > 0 and STRATUM = C / MOSTOT(i) for all PSUs where STRATUM = C
P_STR2_CN = MOSTOT(i) for each PSU where MOSN(i) > 0 and STRATUM = C / MOSTOT(i) for all PSUs where STRATUM = C
P_STR2_CO = MOSTOT(i) for each PSU where MOSO(i) > 0 and STRATUM = C / MOSTOT(i) for all PSUs where STRATUM = C
P_STR2_CY = MOSTOT(i) for each PSU where MOSY(i) > 0 and STRATUM = C / MOSTOT(i) for all PSUs where STRATUM = C
For each funding stream calculate the expected value for Stratum C (EXP_STR4_C FS )
EXP_STR4_CFS = P_STR_C2FS * n_SEL_C
EXP_STR4_C MINFS_C should equal n_SEL_C
b. Calculate the expected value for Stratum D (EXP_STR4_DFS )
Calculate the proportion of the weights of each funding stream in Stratum D (P_STR1_DFS)
P_STR1_DA = MOSTOT(i) for each PSU where MOSA(i) > 0 and STRATUM = D / MOSTOT(i) for all PSUs where STRATUM = D
P_STR1_DD = MOSTOT(i) for each PSU where MOSD(i) > 0 and STRATUM = D / MOSTOT(i) for all PSUs where STRATUM = D
P_STR1_DN = MOSTOT(i) for each PSU where MOSN(i) > 0 and STRATUM = D / MOSTOT(i) for all PSUs where STRATUM = D
P_STR1_DO = MOSTOT(i) for each PSU where MOSO(i) > 0 and STRATUM = D / MOSTOT(i) for all PSUs where STRATUM = D
P_STR1_DY = MOSTOT(i) for each PSU where MOSY(i) > 0 and STRATUM = D /
MOSTOT(i) for all PSUs where STRATUM = D
For each funding stream calculate the expected value for Stratum D (EXP_STR_DFS )
EXP_STR4_DFS = P_STR_DFS * Max(0,(STATEMIN – (n_SEL_A + n_SEL_B+ n_SEL_C)))
EXP_STR4_D MINFS_A, EXP_STR4_D MINFS_B, EXP_STR4_D MINFS_C should equal zero.
c. Calculate the expected value for each funding stream (EXP_STR4 FS )
EXP_STR4 FS = EXP_STR2_A FS + EXP_STR3_B FS + EXP_STR4_C FS + EXP_STR4_D FS
d. Determine the smallest of the expected number of PSUs
Set STR_TESTD = Minimum of (EXP_STR4FS) for all funding streams where P_STR1_DFS > 0
Note: If two or more expected values equal the minimum, the software should use the following order when deciding which funding stream is the minimum: Older Youth, Younger Youth, NEGs, Dislocated Worker, Adults.
Set MINFS_D = the funding stream that has the minimum expected number of PSUs identified in a above. If STR_TESTD >= MIN_STR then n_Sel_D = Maximum of (MIN_STR, (STATEMIN – (n_Sel_A n_Sel_B n_Sel_C)) and STRATUM_NUM = 4 and go to Select PSUs. If STR_TESTD < MIN_STR then Set STRATUM = E for every PSU where MOSMINFS_D = 0 and STRATUM <> A and STRATUM <> B and STRATUM <> C
e. Determine the number of PSUs to select from Stratum D
Count the number of PSUs in Stratum D (N_STR_D)
N_STR_D = Count of PSUs where STRATUM = D
If N_STR_D > (MIN_STR – (EXP_STR2_AMINFS_D + EXP_STR3_B MINFS_D + EXP_STR4_C MINFS_D)) then set n_Sel_D = (MIN_STR – (EXP_STR2_AMINFS_D + EXP_STR3_B MINFS_D + EXP_STR4_C MINFS_D)), else n_Sel_D = N_STR_D.
Stage 5 Stratification
This section of the specification determines how many PSUs to select from stratum E..
a. Calculate the expected value for Stratum D (EXP_STR5_D FS )
If n_Sel_D = N_STR_D then EXP_STR5_D FS = Count of PSU where MOSFS(i) > 0 and STRATUM = D go to calculate the expected value for Stratum E (EXP_STR5_EFS ).
Calculate the proportion of the weights of each funding stream in Stratum D (P_STR2_DFS)
P_STR1_DA = MOSTOT(i) for each PSU where MOSA(i) > 0 and STRATUM = D / MOSTOT(i) for all PSUs where STRATUM = D
P_STR2_DD = MOSTOT(i) for each PSU where MOSD(i) > 0 and STRATUM = D / MOSTOT(i) for all PSUs where STRATUM = D
P_STR2_DN = MOSTOT(i) for each PSU where MOSN(i) > 0 and STRATUM = D / MOSTOT(i) for all PSUs where STRATUM = D
P_STR2_DO = MOSTOT(i) for each PSU where MOSO > 0 and STRATUM = D / MOSTOT(i) for all PSUs where STRATUM = D
P_STR2_DY = MOSTOT(i) for each PSU where MOSY(i) > 0 and STRATUM = D / MOSTOT(i) for all PSUs where STRATUM = D
For each funding stream calculate the expected value for Stratum D (EXP_STR5_D FS )
EXP_STR5_DFS = P_STR_D2FS * n_SEL_D
b. Calculate the expected value for Stratum E (EXP_STR5_EFS )
Calculate the proportion of the weights of each funding stream in Stratum E (P_STR1_EFS)
P_STR1_EA = MOSTOT(i) for each PSU where MOSA(i) > 0 and STRATUM = E / MOSTOT for all PSUs where STRATUM = E
P_STR1_ED = MOSTOT(i) for each PSU where MOSD(i) > 0 and STRATUM = E / MOSTOT(i) for all PSUs where STRATUM = E
P_STR1_EN = MOSTOT(i) for each PSU where MOSN(i) > 0 and STRATUM = E / MOSTOT(i) for all PSUs where STRATUM = E
P_STR1_EO = MOSTOT(i) for each PSU where MOSO(i) > 0 and STRATUM = E / MOSTOT(i) for all PSUs where STRATUM = E
P_STR1_EY = MOSTOT(i) for each PSU where MOSY(i) > 0 and STRATUM = E / MOSTOT(i) for all PSUs where STRATUM = E
For each funding stream calculate the expected value for Stratum E (EXP_STR5_EFS )
EXP_STR5_EFS = P_STR_EFS * Max(0, (STATEMIN – (n_SEL_A + n_SEL_B+ n_SEL_C + n_SEL_D)))
EXP_STR5_EMINFS_A, EXP_STR5_EMINFS_B, EXP_STR5_EMINFS_C, EXP_STR5_EMINFS_D should equal zero.
c. Calculate the expected value for each funding stream (EXP_STR5 FS )
EXP_STR5FS = EXP_STR2_A FS + EXP_STR3_B FS + EXP_STR4_CFS + EXP_STR5_DFS + EXP_STR5_EFS
d. Determine the smallest of the expected number of PSUs
Set STR_TESTE = Minimum of (EXP_STR5FS EXP_STR5_EFS) for all funding streams where P_STR1_EFS > 0. Set MINFS_E = the funding stream that has the minimum expected number of PSUs identified in a above. If STR_TESTE > MIN_STR then n_Sel_E = Maximum of (MIN_STR, (STATEMIN – (n_Sel_A n_Sel_B + n_Sel_C + n_Sel_D)) and STRATUM_NUM = 5 and go to Select PSUs.
e. Determine the number of PSUs to select from Stratum E
Count the number of PSUs in Stratum E (N_STR_E)
N_STR_E = Count of PSUs where STRATUM = E
If N_STR_E > (MIN_STR – (EXP_STR2_AMINFS_E + EXP_STR3_B MINFS_E + EXP_STR4_C MINFS_E+ EXP_STR4_D MINFS_E)) then set n_Sel_E = (MIN_STR – (EXP_STR2_AMINFS_E + EXP_STR3_B MINFS_E + EXP_STR4_C MINFS_E+ EXP_STR4_D MINFS_E)), else n_Sel_D = N_STR_D. Go to Select PSU.
Selecting PSUs
After the software has created strata and determined the number of PSUs to select per stratum, the software must select the PSUs from each stratum. The software will not select PSUs under two conditions: If the user chooses to sample records directly, then the software does not need to select PSUs or if the user chooses to cluster and the number of PSUs is less than or equal to STATEMIN.
In both of these cases, the software skips this section and goes directly to Sampling the Records. If the state chooses to cluster the sample, and the number of PSUs > STATEMIN, then the software must sample PSUs. These samples must be drawn for each stratum (A through E) that contains PSUs. The sampling process for each stratum involves two levels of sampling. First, the software selects the certainty PSUs. By certainty PSU, we are referring to those PSUs that have a high enough proportion of the total composite weight that they must be sampled. Then, the software selects the remaining offices with a probability proportional to the size of the office.
a. Determine the total weight (based upon the C_Weight(j)) for each PSU in the stratum A.
MOSTOT(i) = MOSA(i) + MOSD(i) + MOSN(i) + MOSO(i) + MOSY(i) for each PSU where STRATUM = A
STR_WEIGHTA = MOSTOT(i) for all PSUs where STRATUM = A
b. Calculate the threshold weight to determine if any offices should be selected with certainty.
Divide the total weight of the PSUs in the stratum (STR_WEIGHTA) times 0.8 by the number of offices to be selected in stratum A.
CERT_THR_A = 0.8 * (STR_WEIGHTA / n_Sel_A)
If denominator = 0, then set to 1.
Set PSU_Selected = 0. PSU_Select is a counter to determine if any offices have been selected during the most recent loop through the PSUs.
c. Select the first round of certainty PSUs by comparing the weight of each to the certainty threshold.
Each PSU with a total weight greater than or equal to the certainty threshold is selected with certainty. STR_S (i), where S refers to the Stratum (A, B, C, D, or E) and (i) refers to the specific PSU, identifies the type of PSU. If STR_S (i) = Certainty then the PSU is a certainty PSU. If STR_S (i) = NON then the PSU is a non-certainty PSU. If STR_S (i) is null then the PSU has not been selected as part of the sampled.
If MOSTOT(i) >= CERT_THR_A and STRATUM = A then STR_A(i) = CERTAINTY and PSU_Selected = PSU_Selected + 1. Repeat each PSU in Stratum A.
d. After testing all PSUs in the stratum, the software must determine if another round of testing for certainty offices is necessary. Another round is necessary if PSU_Selected > 0.
If (PSU_Selected = 0 or if the count of PSUs selected => n_Sel_A) then go to Selecting Non-Certainty PSUs.
If PSU_Selected > 0 and the count of PSUs < n_Sel_A then recalculate CERT_THR_A and MOSTOT(i) then, determine the total weight (based upon the C_Weight) for the PSUs in the stratum that have not yet been sampled.
STR_WEIGHTA(i) = MOSTOT(i) for all PSUs where STRATUM = A and S_PSUA(i) is null
Re-calculate the threshold weight to determine if more PSUs should be selected with certainty. Divide the total weight of the remaining PSUs in the stratum (STRWEIGHTA(i)) by the number of PSUs to be selected.
CERT_THR_A = (STR_WEIGHTA / (n_Sel_A-PSU_Selected) )
If denominator = 0, then set to 1.
Note: After the first time through, the process for selecting certainty units differs. We have a higher threshold (CERT_THR_A). If any PSUs in the stratum is equal to or greater than the threshold, then we re-set the threshold to 0.8* CERT_THR_A and select more certainty PSUs. If no PSUs in the stratum achieve the higher threshold, then we do not select any more certainty PSUs.
Threshold2 determines if we need to select any more certainty PSUs from Stratum A. If it has a value of No, then:
Set Values: Set PSU_Selected = 0 and Threshold2 = No. Determine if the first PSU meets the threshold. If so, then reset the threshold and go to Certainty PSU sample 2. If MOSTOT(i) >= CERT_THR_A and STRATUM = A and S_PSUA(i) is null then CERT_THR_A = CERT_THR_A * 0.8 and Threshold2 = Yes and go to Certainty PSU sample 2.
Determine if any PSUs meet the threshold set in the prior step: Repeat D.1.d.2.b.iii.(b) for all PSUs in Stratum A. If no PSUs met the threshold, select non-certainty PSUs. If all PSUs in Stratum A have been tested and Threshold 2 = No, then go to Selecting Non-Certainty PSUs.
Certainty PSU sample 2: If Threshold2 = Yes then do the following:
If MOSTOT(i) >= CERT_THR_A and STRATUM = A and STR_A(i) is null then STR_A(i) = CERTAINTY and PSU_Selected = PSU_Selected + 1. Repeat the prior step for each PSU in Stratum A where S_PSUA(i) is null.
Selecting Non-Certainty PSUs
a. Calculate information needed to sample non-certainty PSUs from Stratum A.
Determine the total weight (based upon the C_Weight(j)) for the certainty PSUs and for the PSUs not yet sampled from the stratum.
STR_WEIGHT_CERTA= MOSTOT(i) for all PSUs where STRATUM = A and S_PSUA(i) = CERTAINTY.
STR_WEIGHT_NONA= MOSTOT(i) for all PSUs where STRATUM = A and S_PSUA(i) is null.
Determine the number of non-certainty PSUs to select (n_SEL_NONCERTA).
n_SEL_NONCERTA= n_Sel_A minus Count of PSUs where STRATUM = A and S_PSUA(i) = Certainty
Determine the number of PSUs not selected with Certainty (N_PSU_RemainA)
N_PSU_RemainA = Count of PSUs where S_PSUA(i) is null
Calculate sampling interval (I_NONCERTA)
I_NONCERTA = STR_WEIGHT_NONA / n_SEL_NONCERTA
If denominator = 0, then set to 1.
b. Select a random number between 0 and I_NONCERTA
Rand_NONCERT = Random number between (0, I_NONCERTA)
c. Create the following variables
Counter is used to track the sum of the weight of records
I_Select is used to track the weight interval used to select records.
i is used as a subscript to identify the PSU(s) under consideration.
N_NONCERTA is used to count the number of non-certainty PSUs that have been sampled.
MOSTOT(i) is the weight of the ith PSU.
d. We set I_Select = Rand_NONCERT.
The software must find the PSU that contains the I_Select weighted unit. Once it has selected this PSU, the software adds I_NONCERTA to I_Select and then finds the PSU that contains this new weighted unit. The process is repeated until (a) n_SEL_NONCERTA PSUs have been selected or (b) until the software has evaluated all the PSUs where S_PSUA(i) is null in the stratum.
Set Counter = 0 and N_NONCERTA = 0 and i = 1 and I_Select = Rand_NONCERT
Do while N_NONCERTA < n_SEL_NONCERTA and i <= N_PSU_RemainA and I_Select <= STR_WEIGHT_NONA.
If I_Select >= Counter and I_Select <= (Counter + MOSTOT(i)) and S_PSUA(i) is null then S_PSUA(i) = Non and N_NONCERTA = N_NONCERTA + 1 and I_Select = I_Select + I_NONCERTA
EndIf
Counter = Counter + MOSTOT(i)
i = i + 1
End Loop
Select PSUs from the remaining strata.
Repeat for all remaining strata that contain PSUs (STRATUM_NUM), that is repeat for STRATUM = B, then for STRATUM = C, etc until certainty and non-certainty PSUs have been selected for all strata that contain PSUs.
Sampling the Records
Sampling Records for Certainty PSUs
a. Combine all records in the adult funding stream FS in Stratum A for all certainty PSUs. In other words, treat all certainty PSUs in a funding stream as one if they were PSU.
b. If PSUType = Records then Randomize all the records in the funding stream being analyzed. Else Sort the records in certainty PSUs in Stratum A by PSU and then by randomize within the PSU.
c. Sum the weights of all records in b.
MOS_Cert_AA = MOSA where STRATUM = A and STR_A(i) = CERTAINTY
d. Calculate the interval by dividing the sum in F.1.c by the number of records to be sampled from certainty PSUs for stratum A and the adult funding stream.
I_Cert_AA = MOS_Cert_AA / n_Cert_STRAA
If denominator = 0, then set to 1.
e. Select a random number between 0 and I_Cert_AA.
Rand_Cert_AA = Random number between (0, I_Cert_AA)
f. Create the following variables
Counter is used to track the sum of the weight of records
I_Select is used to track the weight interval used to select records.
i is used as a subscript to identify the record(s) under consideration.
Num_Sampled is used to count the number of records that have been sampled.
R_Seli is used to identify records that have been selected for the sample.
wi is used to identify the composite weight for the funding stream for the ith record.
g. Determine if how many records there are in the certainty offices for the appropriate funding stream.
Certainty_Rec_STRAA = Count of records for each PSU where Stratum = A and STR_A(i) = CERTAINTY and funding stream = adult
h. We set I_Select = Rand_Cert_AA. The software must find the record that contains the I_Select weighted unit. Once it has selected this record, the software adds I_Cert_AA to I_Select and then finds the record that contains this new weighted unit. The process is repeated until (a) n_Cert_STRAA records have been selected or (b) until the software has evaluated all the records in the funding stream for the PSU (for the certainty PSUs, this refers to all the records in the funding stream that are in certainty PSUs for the stratum).
If Certainty_Rec_STRAA <= n_Cert_STRAA then Select all adult records and repeat.
Set Counter = 0 and Num_Sampled = 0 and i = 1 and I_Select = Rand_Cert_AA.
Do while Num_Sampled < n_Cert_STRAA and i <= Certainty_Rec_STRAA and I_Select <= MOS_Cert_AA
If I_Select >= Counter and I_Select < (Counter + wi) and R_Seli is null then R_Seli = Sampled and Num_Sampled = Num_Sampled + 1 and I_Select = I_Select + I_Cert_AA
Counter = Counter + wi
i = i + 1
EndIf
If I_Select < Counter then I_Select = I_Select + I_NonCert_AA
EndIf
If I_Select >= Counter + wi then Counter = Counter + wi
i = i + 1
EndIf
End Loop
Repeat for all other funding streams (D,N,O,Y) in Stratum A and then for all remaining strata, B, C, D, and E.
Sampling Records for Non-Certainty PSUs
a. Sum the composite weight of all records in FS for first non-certainty PSU 1 in Stratum A that contains adult records. This has been calculated in MOS AA(i).
b. If the number of adult records in PSU 1 is less than or equal to the number of records to be sampled from each non-certainty PSU, select all the records. Determine the number of records in the PSU that are in the funding stream.
Num_Non_PSU1 = Count of records where in PSU1 and STR_A(i) = NON and funding stream = Adult
If Num_Non_PSU1 <= nRec_NonPSU_AA then for each record in PSU1 where funding stream = Adult set R_Seli = Sampled and determine the number of records in the PSU that are in the funding stream. R_Seli identifies if the record has been sampled or not. If R_Seli = Sampled, it has been selected. If it is null, then it has not been selected.
c. Sort the records in this PSU1 by weight from highest to lowest
d. Determine the sampling interval by dividing the weight in F.2.a by the number of records to be sampled from each non-certainty office in Stratum A for the adult funding stream.
I_NonCert_AA = MOS AA(i) /nRec_NonPSU_AA, If denominator = 0, then set to 1.
e. Select a random number between 0 and number of records in PSU1.
Rand_NonCert_AA = Random number between (0,I_NonCert_AA)
f. We can use the sample variables used from the Certainty offices: Counter, I_Select, I, Num_Sampled, R_Seli, wi.
g. We set I_Select = Rand_Cert_AA. The software must find the record that contains the I_Select weighted unit. Once it has selected this record, the software adds I_NonCert_AA to I_Select and then finds the record that contains this new weighted unit. The process is repeated until (a) n_Cert_STRAA records have been selected or (b) until the software has evaluated all the records in the funding stream for the PSU.
Repeat Selecting Records for Non-Certainty PSUs in Stratum A where MOS AA(i) > 0. Repeat Selecting Records for Non-Certainty PSUs for all Non-Certainty PSUs in Stratum A for the remaining funding streams (D, N, O, Y). Repeat Selecting Records for Non-Certainty PSUs and Sampling Records for Certainty PSUs i for all strata, B, C, D, and E that contain records.
2. SCSEP and NFJP Methodological Details
The SCSEP and NFJP sampling algorithms draw a weighted performance sample from those participants who exited during the retention time period. Each record in the retention cohort is assigned a weight of 1, 2, or 3. Records are sampled with a probability proportional to their size. Thus, instead of selecting records directly, records are selected based upon their weight. These details explain how to draw the SCSEP and NFJP validation sample. It provides methodological details on the sample frame (i.e. the universe of records from which the sample will be drawn), the sample size, the weighting scheme, and the selection process.
IMPORTANT NOTE: Several of the variables developed during the sampling process are necessary to calculate the error rates for data element validation. The following fields are particularly important for the calculation: each record’s weight (whether or not the record was sampled), each record R_Seli value, n (the calculated samples size), and n_Non_Cert. In addition, other variables will be needed to test the sampling algorithm once it is programmed.
Calculate the number of enrollments where the participant exited in the retention cohort
N = Count of enrollments where the 4th quarter after the exit quarter is within the report period and (PROJECT_TRANSFER_IND <> “Y” or PROJECT_TRANSFER_IND is null) and PRIOR_GRANTEE_CODE is null and TRANSFERRED_DATE is null and NON_EXIT_REASON <> ii_Transferred_grantee” and TRANSFERRED_GRANTEE_CODE is null and SUB_GRANTEE_CODE <> “RG999” and have zero reject errors on the DQR associated with it, its participant record, or any of its CSA or UE records.
Note: A retention exiter is any enrollment where the 4th quarter after the exit quarter is within the report period.
Calculate the Sample Size
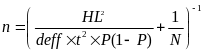
Where n = sample size, HL is the half-length of the confidence interval, N is the number or records, t = 1.96, deff = 2 and P = 0.95. If n is not an integer the number is rounded up to the nearest integer > n.
If Nfs >= 500, then CI = 0.035, Else CI = 0.04
If n > 250, set the sample size = 250.
Assigning Risk Weights to Each Record
For each retention exiter:
Set Risk weight = 3 if this exiter has a UE record with FIRST_QTR_WAGES_TEXT =
“ii_Yes_in-state” OR “iii_Yes_out-of-state” OR “iv_Yes_both_in_and_out” OR “v_Yes_other_admin” OR “vi_Yes_supplemental”
AND
This exiter has a UE record with SECOND_QTR_WAGES_TEXT = “ii_Yes_in-state” OR “iii_Yes_out-of-state” OR “iv_Yes_both_in_and_out” OR “v_Yes_other_admin” OR “vi_Yes_supplemental” OR (SECOND_QTR_WAGES_TEXT = null and SECOND_QTR_WAGES_AMT > 0)
AND
This exiter has a UE record with THIRD_QTR_WAGES_TEXT = “ii_Yes_in-state” OR “iii_Yes_out-of-state” OR “iv_Yes_both_in_and_out” OR “v_Yes_other_admin” OR “vi_Yes_supplemental” OR (THIRD_QTR_WAGES_TEXT = null and THIRD_QTR_WAGES_AMT > 0)
Else set Risk Weight = 2 if this exiter has a UE record with FIRST_QTR_WAGES_TEXT = “ii_Yes_in-state” OR “iii_Yes_out-of-state” OR “iv_Yes_both_in_and_out” OR “v_Yes_other_admin” OR “vi_Yes_supplemental”
Else set Risk Weight = 1
Set key variables for record selection algorithm
Total_Weight = Sum of the Risk weight for all the retention exiters.
Sampling_Interval = Total_Weight/n.
R_Seli is used to identify records that have been selected for the sample, default and initial value = null.
Select first round of records with certainty
Select all records where weight of record >= Sampling_Interval. If this would result in selecting more than n records, randomly select n records where weight of record >= Sampling_Interval. Set R_Seli = “Certainty” for all records selected in this step. Select all records where weight of record >= Sampling_Interval. If this would result in selecting more than n records, randomly select n records where weight of record >= Sampling_Interval. Set R_Seli = “Certainty” for all records selected in this step.
Calculates variables related to the second round of sampling
Total_Weight_Non_Cert = Sum of the Risk Weight for all of the retention exiters whose weight is less than Sampling_Interval.
n_Non_Cert = n – (number of records with weight >= Sampling_Interval).
Sampling_Interval_Non_Cert = Total_Weight_Non_Cert / n_Non_Cert.
Select second round of records with certainty
Select all records where (risk weight >= Sampling_Interval_Non_Cert and R_Seli is null). If this would result in selecting more than n_Non_Cert records, randomly select records with weight 2 until n_Non_Cert records are selected. For all records selected in this step, set R_Seli = “Certainty”.
If certainty records are selected, update and recalculate variables.
If (number of records with weight >= Sampling_Interval_Non_Cert and weight < Sampling_Interval) = 0, skip step 13. If not, set: Total_Weight_Non_Cert = Sum of the Risk Weight for all of the retention exiters whose weight is less than Sampling_Interval_Non_Cert, n_Non_Cert = n – number of records already selected
Sampling_Interval_Non_Cert = Total_Weight_Non_Cert / n_Non_Cert.
Set random variable (needed to sample records)
Random number (R) = Random number between 0 and Sampling_Interval_Non_Cert.
Set variables used to sample records with non-certainty
Counter = 0, which is used to track the sum of the weight of records.
I_Select = R, to track the weight interval used to select records.
i = 1, a subscript to identify the record(s) under consideration.
Num_Sampled = 0, to count the number of records that have been sampled.
wi, to identify the weight for the ith record.
If all records are to be sampled, select all records
If n_Non_Cert >= number of records not sampled, select all records, and set R_Seli = “Certainty” for all records.
If the number of records sampled is less than the number of records to be sampled with non-certainty
Do while Num_Sampled < n_Non_Cert
a. If the current record has already been selected for sampling, go to the next record:
If (R_Seli is not null) then
i = i + 1
EndIf
b. If the current record contains the I_Select weighted unit, select the record, up the number of records sampled, up the I_Select weighted unit, up the weight counter and go to the next record.
Else If I_Select >=Counter and I_Select < (Counter + wi) then
R_Seli = “Random”
Num_Sampled = Num_Sampled + 1
I_Select = I_Select + Sampling_Interval_Non_Cert
Counter = Counter + wi
i = i + 1
EndIf
c. If the I_Select weighted unit is less than the counter, then update the I_Select.
Else If I_Select < Counter then
I_Select = I_Select + Sampling_Interval_Non_Cert
EndIf
d. If the I_select unit is greater than or equal to the counter plus the next record, up the counter and the record.
Else If I_Select >= Counter+ wi then
Counter = Counter + wi
i = i + 1
EndIf
B. Estimation Procedure
For report validation, the states and grantees compare their annual reported values to the validation values to determine if the error rate is within an acceptable range. ETA maintains report validation error reports and addresses discrepancies as they arise. Furthermore, states with report validation error rates in excess of 2% are not eligible for incentive grants.
For data element validation, estimation encompasses computing sample weights and error rates. Validators compare the data from the samples to source documentation. Once all the data have been evaluated, error rates are calculated for each data element. These error rates are estimated using data weighted to account for differences in probability of selection. The validation software computes the sampling errors for each state or grantee (specific details are below in parts 1 and 2), taking into account the multistage design and the use of unequal weights.
1. WIA Title IB and TAA Error Rate Calculation
After users have completed the validation, the software must calculate the two weighted error rates. The overall error rate for a data element within a funding stream equals the number of errors divided by the number of records sampled, weighted to account for the composite weight of the records and the clustering. The reported data error rate for a data element within a funding stream equals the number of errors divided by the number of records that are validated for the specific data element, weighted to account for the composite weight of the records and the clustering.
To calculate the error rates, the software must calculate the following values:
For each PSU sampled, the software must calculate the probability of selection for the PSU (P_PSU(i) ). For certainty PSUs, PPSU = 1.For each record sampled, the software must calculate the probability of selection for that record (P_Rec(j)). The software must calculate an error weight (Error_w(j)) that is used to calculate the error rates for each data element being validated. This value is equals the inverse of P_PSU(i) * P_Rec(j).
Calculating the Probability of Selection for each PSU
For Certainty PSUs or if PSUType = Records
PPSU = 1.
For Non-Certainty PSUs
P_PSU(i) = MOSTOT(i) * n_Sel_NonCertA / MOSTOT(i) where STRATUM = A and STR_A(i) = Non or STR_A(i) is null.
Calculating the Probability of Selection for each Record Sampled
Certainty PSUs
For Certainty PSUs, the software calculates the probability of selection for each record sampled by taking the composite weight of the record for the funding stream for which it was selected and dividing the product by the sum of the composite weights of all records in the strata that were selected from certainty offices for the appropriate funding stream. This number is then multiplied by the number of records sampled for the funding stream from certainty PSUs in the funding stream. If a record is selected for more than one funding stream, then a separate weight must be calculated for each funding stream.
If n_Sampled_Cert_A Adult = Count of Records where STRATUM = A and FS = adult and STR_A(i) = CERTAINTY then P_Rec(j) = 1 for all sampled records where STRATUM = A and FS = adult and STR_A(i) = CERTAINTY.
Else P_Rec(j) = C_weight Adult(j) * n_Sampled_Cert_A Adult for Funding Stream = Adults and STRATUM = A and STR_A(i) = CERTAINTY / C_weight(Adult(j)) where STRATUM = A and Funding Stream = Adults and STR_A(i) = CERTAINTY where n_Sampled_Cert_A Adult = the number of records selected as part of the sample from certainty offices in PSU A where FS = Adult.
Note: In the ideal situation, n_Sampled_Cert_A Adult = n_Cert_STRAA, but in some situations n_Sampled_Cert_A Adult < n_Cert_STRAA
Repeat the step above to calculate P_Rec(j) for each record sampled in the funding stream being analyzed from the certainty PSUs in stratum A. Repeat to calculate P_Rec(j) for the remaining funding streams (D, N, O, Y) sampled from certainty PSUs in stratum A. Repeat to calculate P_Rec(j) for records sampled certainty PSUs in the remaining strata (B, C, D, E).
Non-Certainty PSUs
For non-certainty PSUs, the software calculates the probability of selection for each record sampled by taking the composite weight of the record for the funding stream for which it was selected and dividing it by the sum of the composite weights of all records in the PSU that were in the appropriate funding stream. This number is then multiplied by the number of records selected from the PSU. If a record is selected for more than one funding stream, then a separate weight must be calculated for each funding stream.
If n_Sampled_A Adult(i) = Count of Records where STRATUM = A and FS = adult and PSU = i then P_Rec(j) = 1 for all sampled records from PSU = i.
Else
P_Rec(j) = C_weight Adult(j) * n_Sampled_A Adult(i) for Funding Stream = Adults and STRATUM = A and PSU = i / C_weight(Adult(j)), where STRATUM = A and Funding Stream = Adults and PSU = I, where n_Sampled_A Adult = the number of records sampled from PSU = i where FS = Adult. Repeat the step above to calculate P_Rec(j) for each record sampled from PSU = i in stratum A. Repeat to calculate P_Rec(j) for the remaining funding streams (D, N, O, Y) sampled from PSU = i in stratum A. Repeat to calculate P_Rec(j) for the remaining non-certainty PSUs in stratum A. Repeat to calculate P_Rec(j) for records sampled from non-certainty PSUs in the remaining strata (B, C, D, E).
Calculating the Error Weight for each Record Sampled
For each record, it is necessary to calculate the error weight (Error_w(j)) for each record sampled for validation. This is used to calculate the error rates for each data element being validated. If a record is sampled in more than one funding stream, separate error weights must be calculated for each funding stream.
Error_w(j) = (P_PSU(i) * P_Rec(j))-1
Repeat for each record where P_Rec(j) is not null.
Calculating the Error Rates for each Data Element
Two error rates must be calculated for each data element validated. The numerator is the same for both – the sum of the error weights for those records for which the appropriate data element failed. The denominators differ. For the reported data error rate, the denominator equals the sum of the error weights for all records sampled for the funding stream that should be validated. On the other hand, the overall error rate denominator equals the sum of the error weights for all records sampled for the funding stream. Because users can constantly change their validation results, the results need to be calculated when opened.
REPORTED DATA ERROR RATE = (Error_w(j) * P_FDE) for each record sampled for the appropriate funding stream / (Error_w(j) * VAL(j)) for each record sampled for the appropriate funding stream, where P_FDE = 1 if the element failed the validation and P_FDE = 0 if the element passed the validation or if the state was not required to validate the element for this record.
VAL(j) = 1 if the state was required to validate the element for the record. VAL(j) = 0 if the state was not required to validate the element for the record.
OVERALL ERROR RATE = (Error_w(j) * P_FDE) for each record sampled for the appropriate funding stream / Error_w(j) for each record sampled for the appropriate funding stream, where P_FDE = 1 if the element failed the validation and P_FDE = 0 if the element passed the validation or if the state was not required to validate the element for this record. The software must calculate the above error rates for each element selected for validation by funding stream.
2. SCSEP and NFJP Error Rate Calculation
The first step to calculating the weight is to determine the probability of selection for each record. This is used to calculate the record’s error weight, which determines how it impacts the error rate calculations. To calculate the error rates, the weights of the records that are in error are divided by the weights of all records validated, or all records sampled depending on the type of error rate calculation. Error rates are calculated for each data element.
For each record, set Error_w(j) = 1/p_selectioni, p_selectioni = 1 if (R_seli = Certainty), else
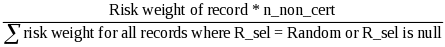
Two error rates must be calculated for each data element validated. The numerator is the same for both – the sum of the error weights for those records for which the appropriate data element failed. The denominators differ. For the reported data error rate, the denominator equals the sum of the error weights for all records sampled for the funding stream that should be validated. On the other hand, the overall error rate denominator equals the sum of the error weights for all records sampled for the funding stream. Because users can constantly change their validation results, the results need to be calculated when opened.
REPORTED DATA ERROR RATE = (Error_w(j) * P_FDE) for each record sampled/ (Error_w(j) * VAL(j)) for each record sampled, where P_FDE = 1 if the element failed the validation and P_FDE = 0 if the element passed the validation or if the grantee was not required to validate the element for this record.
VAL(j) = 1 if the grantee was required to validate the element for the record. VAL(j) = 0 if the grantee was not required to validate the element for the record.
OVERALL ERROR RATE = (Error_w(j) * P_FDE) for each record sampled for the / Error_w(j) for each record sampled, where P_FDE = 1 if the element failed the validation and P_FDE = 0 if the element passed the validation or if the grantee was not required to validate the element for this record.
Note that each data element gets its own error rate calculation.
C. Degree of Accuracy Needed for Purpose Described in the Justification
For data validation to be effective and to allow for continuous improvement, ETA has established acceptable levels for the accuracy of reports and data elements in their incentives and sanctions process. Error rates for report validation and data element validation have been established independently of one another based on the analysis of validation efforts currently underway. For states to be eligible for incentives and sanctions, they must have submitted timely report validation summaries with error rates less than 2 percent. Data element validation errors rates vary by size, ranging from 4 percent for small states and grantees and 3.5 percent for large states and grantees.
D. Unusual Problems Requiring Specialized Sampling Procedures
The discussion above indicates that the methodology uses specialized sampling procedures. These rational for using these procedures rather than pure stochastic methods are to minimize the burden that data element validation imposes upon the states and grantees.
3. Response Rates
As mentioned in Part 1, response rate issues do not arise in the data validation program. Data validation relies on existing records from state and grantee management information systems and case files. Through the use of valid sampling techniques, the validation process results in estimates of data accuracy that can be generalized to the universe of data reported to ETA on program performance and activities.
4. Tests of Procedures or Methods
WIA Title IB, Wagner-Peyser, and TAA program staff have been conducting data validation for six years; the NFJP and SCSEP has been conducting validation for five years. The states and grantees received training prior to beginning validation and receive ongoing training and technical assistance from ETA’s data validation contractor throughout the validation process. Results of these data validation activities indicate that the methodology has functioned as intended and has enabled states to identify and address reporting errors.
5. Individuals Consulted on Statistical Aspects of the Design
William S. Borden Senior Fellow Mathematica Policy Research, Inc. (609) 275-2321
|
Donsig Jang Senior Statistician Mathematica Policy Research, Inc. (202) 484-4246
|
John Eltinge Assistant Commissioner for Survey Method Research Bureau of Labor Statistics U.S. Department of Labor (202) 691-7404
|
Jonathan Ladinsky Senior Program Analyst Mathematica Policy Research, Inc. (609) 275-2250
|
John Hall Senior Sampling Statistician Mathematica Policy Research, Inc. (609) 799-3535 |
|
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | SUPPORTING STATEMENT FOR REQUEST FOR OMB APPROVAL |
| Author | aeyoung |
| File Modified | 0000-00-00 |
| File Created | 2021-01-28 |
© 2026 OMB.report | Privacy Policy