Appendix K: Power Calculations
Appendix K_Power Calculations.docx
Program Evaluation of the Partnership for International Research and Education (PIRE) Program
Appendix K: Power Calculations
OMB: 3145-0236
Appendix K: Power Calculations
Two-Sample Test of Means
This appendix contains our power calculations to determine the sample sizes needed to detect specified minimum detectable effect sizes (for continuous outcomes) or standardized minimal detectable differences (for dichotomous outcomes). First we present the power calculations for continuous outcomes, followed by the power calculations for dichotomous outcomes.
Let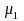 denote the population mean in the PIRE group and let
denote the population mean in the PIRE group and let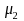 denote the population mean in the comparison group.
denote the population mean in the comparison group.
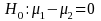 vs.
vs.
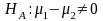
Let
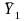 denote the estimated mean in the PIRE group and let
denote the estimated mean in the PIRE group and let
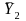 denote the estimated mean in the comparison group. Let
denote the estimated mean in the comparison group. Let
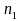 and
and
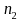 be
the sample sizes of the PIRE and comparison groups respectively and
be
the sample sizes of the PIRE and comparison groups respectively and
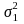 and
and
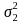 be the sample variances of the PIRE and comparison groups
respectively, after controlling for covariates.
be the sample variances of the PIRE and comparison groups
respectively, after controlling for covariates.
Then
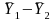 can be used as an estimator for
can be used as an estimator for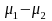 ;
;
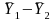 ~
N
~
N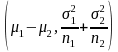
The formula that relates effect size, power and sample size is
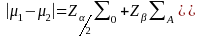 ;
where
;
where
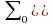 is the variance under the null hypothesis and
is the variance under the null hypothesis and
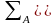
is the variance under the alternative hypothesis.
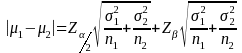
If
we assume that
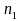 =
=
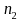 =
=
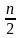 then
then
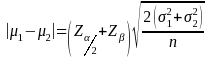
Hence,
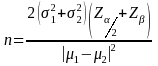
The sample size calculations were made under the following assumptions:
A two-sided statistical test at the standard 5 percent significance level was used (α = 0.05);
Standardized effect sizes of 0.02, 0.05, 0.10, 0.15, 0.20, 0.35, 0.6, and 0.7 in the difference between PIRE participants and similar participants in the comparison group for outcomes of interest will be detected;
The standardized effect sizes will be detected with 80% power (1-β = 0.80);
The sample sizes needed from each group were set to equal;
The proportion of variance explained by covariates was estimated to be 10 percent;1
Sample sizes were adjusted to account for potential response rates based on the evaluation of the EAPSI (graduate student fellowship) program. In this evaluation, response rates for EAPSI fellows and unfunded EAPSI applicants were 73 and 46 percent, respectively.2
Exhibit K.1 below shows the sample size of graduate students needed for (comparative analyses using the assumptions made above.
For example, to detect a standardized effect size of 0.2 with 80 percent power in the difference between PIRE and Comparison project graduate students, we will need an analysis sample of size 706 (353 in both groups) assuming a two-sided test at 5% level of significance and that covariates explain 10 percent of the variance.
Assuming
a 73 percent response rate among graduate students in the PIRE group,
we will need to select a PIRE sample of size 484 in order to achieve
an analysis sample of size
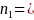 353
(i.e., 353/0.73 = 484). Also, assuming a 46 percent response rate
among graduate
students in the Comparison group,
we will need to select a sample of 767 in order to achieve an
analysis sample of size
353
(i.e., 353/0.73 = 484). Also, assuming a 46 percent response rate
among graduate
students in the Comparison group,
we will need to select a sample of 767 in order to achieve an
analysis sample of size
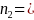 353
(i.e., 353/0.46= 767).
353
(i.e., 353/0.46= 767).
Exhibit K.1: Power calculations and Sample Sizes for graduate students |
||||||||||
|
Size of Analysis Sample |
Size of Selected Sample |
||||||||
Obs |
alpha |
power |
std_es |
var1 |
var2 |
n |
n1 |
n2 |
n1_adj |
n2_adj |
1 |
0.05 |
0.8 |
0.02 |
0.9 |
0.9 |
70640 |
35320 |
35320 |
48384 |
76783 |
2 |
0.05 |
0.8 |
0.05 |
0.9 |
0.9 |
11302 |
5651 |
5651 |
7741 |
12285 |
3 |
0.05 |
0.8 |
0.10 |
0.9 |
0.9 |
2826 |
1413 |
1413 |
1936 |
3072 |
4 |
0.05 |
0.8 |
0.15 |
0.9 |
0.9 |
1256 |
628 |
628 |
860 |
1365 |
5 |
0.05 |
0.8 |
0.20 |
0.9 |
0.9 |
706 |
353 |
353 |
484 |
767 |
6 |
0.05 |
0.8 |
0.35 |
0.9 |
0.9 |
231 |
116 |
116 |
159 |
252 |
7 |
0.05 |
0.8 |
0.60 |
0.9 |
0.9 |
78 |
39 |
39 |
53 |
85 |
8 |
0.05 |
0.8 |
0.70 |
0.9 |
0.9 |
58 |
29 |
29 |
40 |
63 |
Notes:
Alpha: Level of significance
Power: Power
std_es: Standardized Effect Size we wish to detect
var1: 1 (percent of variance explained by covariates)
var2: 1 (percent of variance explained by covariates)
n: Total Analysis Sample Size Required
n1: PIRE Group: Analysis Sample Size Required
n2: Comparison Group: Analysis Sample Size Required
n1_adj: PIRE Group: Size of sample needed in order to obtain analysis sample size assuming a response rate of 73 percent.
n2_adj: Comparison Group: Size of sample needed in order to obtain analysis sample size assuming a response rate of 46 percent
Two-Sample Test of Proportions
Let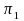 denote the population proportion of “success” in the PIRE
group and let
denote the population proportion of “success” in the PIRE
group and let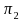 denote the population proportion of “success” in the
comparison group. “Success,” in this usage refers only
to the likelihood that an outcome was observed for a given
individual. For example, if the outcome of interest is “accepted
an international-based postdoctoral fellowship upon receipt of PhD”
for a graduate student, then the two-sample test of proportions
indicates the smallest difference in the percentages of PIRE and
Comparison group graduate students for whom that outcome was observed
that the evaluation can detect.
denote the population proportion of “success” in the
comparison group. “Success,” in this usage refers only
to the likelihood that an outcome was observed for a given
individual. For example, if the outcome of interest is “accepted
an international-based postdoctoral fellowship upon receipt of PhD”
for a graduate student, then the two-sample test of proportions
indicates the smallest difference in the percentages of PIRE and
Comparison group graduate students for whom that outcome was observed
that the evaluation can detect.
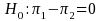 vs.
vs.
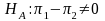
Let
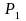 denote the estimated proportion of “success” in the PIRE
group and let
denote the estimated proportion of “success” in the PIRE
group and let
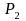 denote the estimated proportion of “success” in the
comparison group. Let
denote the estimated proportion of “success” in the
comparison group. Let
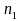 and
and
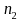 be
the sizes of the analysis samples of the PIRE and comparison groups
respectively, and let
be
the sizes of the analysis samples of the PIRE and comparison groups
respectively, and let
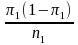 and
and
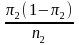 be the sample variances of the PIRE and comparison groups
respectively, after controlling for covariates.
be the sample variances of the PIRE and comparison groups
respectively, after controlling for covariates.
Then
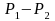 can be used as an estimator for
can be used as an estimator for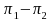 ;
;
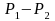 ~
N
~
N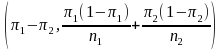
The formula that relates effect size, power and sample size is:
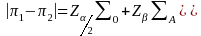 ;
where
;
where
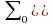 is the variance under the null hypothesis and
is the variance under the null hypothesis and
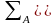 is the variance under the alternative hypothesis.
is the variance under the alternative hypothesis.
Assume
that
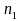 =
=
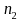 =
=
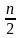
Under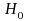 ,
,
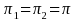 (common
null have which by convention is set to
(common
null have which by convention is set to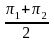 )
)
hence
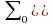 =
=
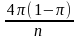 and
and
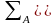 is
is
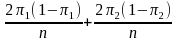
So
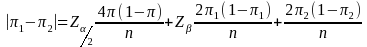
Hence,
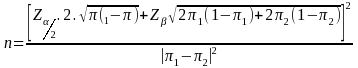
The sample size calculations were made under the following assumptions:
A two-sided statistical test at the standard 5 percent significance level was used (α = 0.05).
Differences of 0.01, 0.04, 0.05, 0.07, 0.08, 0.10, and 0.20 between PIRE and Comparison group participants in proportion of success (i.e., 1, 4, 5, 7, 8, 10, and 20 percentage point differences between groups) will be detected.
The effects will be detected with 80 percent power (1-β = 0.80).
The sample size in both groups were set to equal
The probability of success in the PIRE group is: 0.10 to 0.803.
This sample size was adjusted to account for potential response rates based on the evaluation of the EAPSI (graduate student fellowship) program. In this evaluation, response rates for EAPSI fellows and unfunded applicants were 73 and 46 percent, respectively.
Exhibit K.2 shows the required sizes of selected and analysis samples for graduate students under various scenarios. For example, assuming we require a two-sided test at 5 percent level of significance, and 80 percent power, the probability of success in the PIRE group is 0.5, and given the response-rate assumptions above, the required sample sizes for detection of an ten percentage point difference between the two groups of graduate students are selected samples of 479 and 705 yielding analysis samples of sizes 388 and 388 in the PIRE and comparison groups, respectively.4
Note that the sample size estimates in the table vary by the proportion of success of the outcome in the PIRE group. The table below displays sample size estimates for various proportion of success of the outcome in the PIRE group (pi1=0.4, 0.5, 0.6 and 0.7).
Exhibit K.2: Minimum detectable differences (in proportions) for given sample sizes for specified proportion observed in the PIRE group of graduate students |
||||||||||
|
Size of Analysis Sample |
Size of Selected Sample |
||||||||
Obs |
alpha |
power |
diff |
pi1 |
pi2 |
n |
n1 |
n2 |
n1_adj |
n2_adj |
1 |
0.05 |
0.8 |
0.01 |
0.1 |
0.09 |
26990 |
13495 |
13495 |
16660 |
24536 |
2 |
0.05 |
0.8 |
0.04 |
0.1 |
0.06 |
1442 |
721 |
721 |
890 |
1311 |
3 |
0.05 |
0.8 |
0.05 |
0.1 |
0.05 |
869 |
435 |
435 |
537 |
791 |
4 |
0.05 |
0.8 |
0.07 |
0.1 |
0.03 |
387 |
194 |
194 |
240 |
353 |
5 |
0.05 |
0.8 |
0.08 |
0.1 |
0.02 |
274 |
137 |
137 |
169 |
249 |
6 |
0.05 |
0.8 |
0.10 |
0.1 |
0.00 |
147 |
74 |
74 |
91 |
135 |
7 |
0.05 |
0.8 |
0.20 |
0.1 |
0.10 |
71 |
36 |
36 |
44 |
65 |
1 |
0.05 |
0.8 |
0.01 |
0.2 |
0.19 |
49281 |
24641 |
24641 |
30421 |
44802 |
2 |
0.05 |
0.8 |
0.04 |
0.2 |
0.16 |
2894 |
1447 |
1447 |
1786 |
2631 |
3 |
0.05 |
0.8 |
0.05 |
0.2 |
0.15 |
1811 |
906 |
906 |
1119 |
1647 |
4 |
0.05 |
0.8 |
0.07 |
0.2 |
0.13 |
880 |
440 |
440 |
543 |
800 |
5 |
0.05 |
0.8 |
0.08 |
0.2 |
0.12 |
657 |
329 |
329 |
406 |
598 |
6 |
0.05 |
0.8 |
0.10 |
0.2 |
0.10 |
398 |
199 |
199 |
246 |
362 |
7 |
0.05 |
0.8 |
0.20 |
0.2 |
0.00 |
68 |
34 |
34 |
42 |
62 |
1 |
0.05 |
0.8 |
0.01 |
0.5 |
0.49 |
78479 |
39240 |
39240 |
48444 |
71345 |
2 |
0.05 |
0.8 |
0.04 |
0.5 |
0.46 |
4895 |
2448 |
2448 |
3022 |
4451 |
3 |
0.05 |
0.8 |
0.05 |
0.5 |
0.45 |
3129 |
1565 |
1565 |
1932 |
2845 |
4 |
0.05 |
0.8 |
0.07 |
0.5 |
0.43 |
1592 |
796 |
796 |
983 |
1447 |
5 |
0.05 |
0.8 |
0.08 |
0.5 |
0.42 |
1216 |
608 |
608 |
751 |
1105 |
6 |
0.05 |
0.8 |
0.10 |
0.5 |
0.40 |
775 |
388 |
388 |
479 |
705 |
7 |
0.05 |
0.8 |
0.20 |
0.5 |
0.30 |
186 |
93 |
93 |
115 |
169 |
1 |
0.05 |
0.8 |
0.01 |
0.8 |
0.79 |
51164 |
25582 |
25582 |
31583 |
46513 |
2 |
0.05 |
0.8 |
0.04 |
0.8 |
0.76 |
3365 |
1683 |
1683 |
2078 |
3060 |
3 |
0.05 |
0.8 |
0.05 |
0.8 |
0.75 |
2187 |
1094 |
1094 |
1351 |
1989 |
4 |
0.05 |
0.8 |
0.07 |
0.8 |
0.73 |
1150 |
575 |
575 |
710 |
1045 |
5 |
0.05 |
0.8 |
0.08 |
0.8 |
0.72 |
892 |
446 |
446 |
551 |
811 |
6 |
0.05 |
0.8 |
0.10 |
0.8 |
0.70 |
586 |
293 |
293 |
362 |
533 |
7 |
0.05 |
0.8 |
0.20 |
0.8 |
0.60 |
162 |
81 |
81 |
100 |
147 |
Notes:
Alpha: Level of significance
Power: Power
Diff: Difference we wish to detect
pi1: Probability of Success in PIRE Group
pi2: Probability of Success in Comparison Group
n: Total Analysis Sample Size Required
n1: PIRE Group: Analysis Sample Size Required
n2: Comparison Group: Analysis Sample Size Required
n1_adj: PIRE Group: Size of sample needed in order to obtain analysis sample size assuming a response rate of 73%.
n2_adj: Comparison Group: Size of sample needed in order to obtain analysis sample size assuming a response rate of 46%
For undergraduate respondents (PIRE only), a sample size was chosen to produce estimates with a precision of less than .05. Assuming a simple random sample and 95 percent confidence level Exhibit K.3 shows the sample size needed for various levels of precision. Sample size is calculated as (1.96)2 *(p*(1p))/(Precision)2, where p was set equal to 0.50.
Exhibit K.3: Precision of estimates for given census size of PIRE undergraduates |
|
N of respondents |
precision |
600 |
.04 |
474 |
0.045 |
384 |
0.05 |
317 |
.055 |
1 We have assumed that covariates will explain 10 percent of the variance because pre-participation measures of key outcomes will be included in the model.
2 Actual sample sizes for the PIRE evaluation may be higher because all participants will have taken part in a PIRE or comparison project and they will have participated more recently than the earliest cohort of EAPSI (2000) fellows. In other words, in the evaluation of PIRE, comparison group members are not denied applicants for NSF funding (in contrast to the comparison group used in the EAPSI evaluation).
3 These proportions of “success” are based on empirical data from the EAPSI evaluation, where the “success” is that of EAPSI fellows for the following outcomes: a) employment outside the U.S. since year marking end of fellowship period; b) in current job, works with individuals located in other countries; c) in current job, work with individuals in other countries includes joint publications and/or jointly-developed products; d) type of current work with individuals in other countries includes joint publications and/or jointly-developed products; e) has mentored others from the U.S. traveling to another country to conduct research; f) conducted activities to foster international collaboration; g) engages in one or more activities to foster international collaboration.
4 That is, 50 versus 30 percent “success” in PIRE and comparison groups, respectively.
Appendix
K: Power Calculations
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Carter Epstein |
| File Modified | 0000-00-00 |
| File Created | 2021-01-27 |
© 2026 OMB.report | Privacy Policy