Analysis Plan for Web Experiment
Appx R_Analysis Plan for Web Experiment_4_16_19.docx
Consumer Research on the Safe Handling Instructions Label for Raw and Partially Cooked Meat and Poultry Products and Labeling Statements for Ready-to-Eat and Not-Ready-to-Eat Products
Analysis Plan for Web Experiment
OMB: 0583-0177
Appendix R:
Analysis
Plan for the Web-Based Experimental Study
The primary aims of the web-based experimental study are (1) to identify three SHI labels with the highest degree of salience, where salience is the label’s ability to draw participants’ attention when placed on a typical food package, and (2) to identify three rationales that convey the importance of complying with the information presented on the SHI label. The first aim, identification of the three most salient SHI labels, will employ methods from Signal Detection Theory (MacMillan, 2002). Specifically, we infer salience based on the participants’ ability to accurately discriminate information that was presented as part of a stimulus (for this study, a mock food package) from information that was not presented as part of the stimulus. Our approach, described in detail below, includes a continuous measure constructed from eight binary (yes/no) items and a set of Receiver-Operator Characteristic (ROC) curves constructed from Likert-type items quantifying the participants’ confidence in their discrimination decisions. The former measure is useful because it can be used to construct the omnibus F-test of statistical significance across the 27 experimental conditions. The latter measure is useful because it provides a more robust interpretation of label salience. The second aim uses a ranked voting procedure with vote reassignment to select the three rationale statements that best convey the importance of complying with the SHI label information based on participants’ responses.
R.1 Primary Outcome: Awareness of SHI Label
First, we will conduct an omnibus test to address the null hypothesis that there are no statistically significant differences among salience scores for the 27 labels. The omnibus test uses a measure constructed from eight dichotomous (yes/no) items (Questions 6−13 in the survey, Appendix B). Each item asks the participant to report whether an icon or word phrase (i.e., element) was present on a previously viewed food package, with some of the elements pertaining to features of the SHI label. The item set is balanced to include the same number of hits (H) (i.e., presentation of an element that was part of the package) and false alarms (F) (i.e., presentation of an element that was not part of the package). For each hit, the participant receives one point (+1) for a correct answer (yes), and zero otherwise. For each false alarm, the participant receives one point (+1) for each incorrect answer (yes), and zero otherwise. The number of hits and false alarms reported can be summarized as proportions and transformed to z-scores so that each participant’s hit rate and false alarm rate are realizations from a unit-normal distribution. These two pieces of information are used to calculate the individual’s ability to accurately differentiate elements that were present from those that were not (d’). This is accomplished using the following formula:
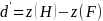
where
z(H) is the z-score corresponding to the proportion of correct hits.
z(F) is the z-score corresponding to the proportion of incorrect false alarms.
According to this formula, a participant’s visual salience is defined as the difference between true positive responses and false negative responses. Labels with higher positive mean values indicate that participants were more attentive to the visual target (i.e., high salience).
We will use a one-way analysis of variance (ANOVA) to examine the null and alternative hypotheses:
Ho: There is no statistically significant difference among the salience scores for the 27 label formats.
Ha: There is a statistically significant difference, indicating that the salience score for at least 1 of the 27 label formats differs from the remaining salience scores.
One-way ANOVA is an appropriate statistical analysis when the purpose of research is to assess if mean differences exist on one continuous dependent variable by an independent variable with two or more discrete groups. The dependent variable in this analysis is d’, the measure of visual salience, and the independent variable is study condition (i.e., SHI label format). The t test will be two-tailed with the probability of rejecting the null hypothesis when it is true set at p < .05. Following the main hypothesis test, the 27 SHI label formats will be rank ordered from highest to lowest based on salience score. The top three SHI label formats based on rank will be retained.
Second, for each of the three retained SHI labels, we will address the null hypothesis that observed salience is no different than chance using a set of empirical ROC curves. A ROC curve uses the hit rates and false alarm rates to calculate the true-positive response rate (sensitivity) and the false-positive response rate (1 – specificity). These data are plotted with sensitivity (0% to 100%) along the y-axis and 1 – specificity (0% to 100%) along the x-axis. The ROC curve could be expressed based on the binary (yes/no) response, but this requires assumptions about the distributional properties of the data because the binary data do not provide enough data points to accurately describe the curve (Hanley & McNeil, 1982). In contrast, a more accurate description of the label’s salience can be achieved with a full (i.e., empirical) expression of the ROC curve. This is accomplished using a set of confidence rating items that, in effect, vary the participant’s decision criteria.1 The rating task items ask respondents to indicate a level of confidence corresponding to their decision that the presented stimulus was (or was not) part of the SHI label. Confidence is rated on a 7-point scale, with semantic anchors “not at all sure” and “very sure.” Recognizing that lower levels of confidence are nested within higher levels of confidence, we can quantify hit rates and false-alarm rates across a range of decision criteria. In other words, for anyone who reported the highest level of confidence (very sure or 7) for a particular item, it is inferred that they also have confidence at lower levels, and so on. This process generates a (k−1) by 2 data matrix of probability values, where k indicates the number of levels in the confidence scale and the paired probabilities are the Cartesian (i.e., x-values and y-values) coordinates used to express the ROC curve.
We will examine the ROC curves by specifying a series of logistic regression models, one for each of the five top-ranked SHI labels, and using ROC curve analytic tools available in the SAS logistic regression procedure (SAS, 2013). An example of the logistic regression model follows:
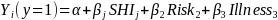
where
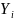 is
the log odds (i.e., the predicted probability) of success for the ith
person exposed to the jth SHI
label, after controlling for risk preference (Risk) and
whether the participant reported that a member of their household had
ever experienced a foodborne illness (Illness).2
For each ROC curve, we will calculate the area under the curve (AUC)
and assess each curve against the null hypothesis of chance
association and alternative hypothesis:
is
the log odds (i.e., the predicted probability) of success for the ith
person exposed to the jth SHI
label, after controlling for risk preference (Risk) and
whether the participant reported that a member of their household had
ever experienced a foodborne illness (Illness).2
For each ROC curve, we will calculate the area under the curve (AUC)
and assess each curve against the null hypothesis of chance
association and alternative hypothesis:
Ho: Participants’ ability to recognize elements of the SHI label, as observed in the ROC curve, was not better than chance.
Ha: Participants recognized SHI label elements, as observed in the ROC curve, at a rate that was beyond chance.
AUCs represent the proportion of the Cartesian space below the ROC curve. A line from point (0,0) to point (1,1) bisects the space and is equivalent to an AUC of .50, indicating that participants’ responses to SHI label elements were no better than random guesses. Accordingly, AUCs that are statically different from .50 indicate that participants were able to distinguish SHI label elements from distractors. Our statistical model will estimate the AUC and the Wald confidence interval (CI) around the AUC. When the CI does not include .50, we reject the null hypothesis of chance association.
R.2 Follow-Up Analyses: Awareness of SHI Label
Follow-up analyses examine participants’ ability to properly recall the location of the SHI as an additional indication of salience. Based on a single item that asks all participants to “Use your mouse to POINT to the spot where you saw information about how to safely prepare this food product,” we will create a dichotomous indictor that classifies participants who correctly identify the location of the SHI label (their mouse click is within the SHI label space on the package) and participants who misidentify the location of the SHI label. Chi-square goodness-of-fit tests will be used to examine the null and alternative hypotheses:
Ho: There will be no difference among the SHI label groups in the proportion of participants who accurately identify the location of the SHI label presented during the exposure phase.
Ha: The proportion of participants who accurately identify the location of the SHI labels will be significantly different for at least one of the selected SHI label groups.
The chi-square is an appropriate statistical test when the purpose of the research is to examine the relationship between two nominal-level variables (Pett, 1997). For this study, those variables are SHI label (3 levels) and accurate identification of the SHI position (yes/no). To conduct the chi-square test, we will summarize the data in a 3-by-2 frequency table defined by the categories of the nominal variables. We will then compare the observed value in each cell (Oij) with the expected value for each cell (Eij), which is the product of the row (Ri) and the column (Cj) divided by the total sample (N), and the chi-square statistic is generated with the following formula:
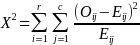 .
.
To evaluate the significance of the results, we will compare the calculated chi-square coefficient (X2) and the critical-value coefficient. When the calculated value is larger than the critical value, with alpha of 0.05, we will reject the null hypothesis (suggesting a statistically significant relationship). To determine the degrees of freedom (df) for a chi-square test, we must use the following equation:
 .
.
The r value equals the number of rows, and the c value equals the number of columns. For a chi-square test to provide a valid result, several conditions and assumptions must be met. The data must be random samples of multinomial mutually exclusive distributions, and the expected frequencies should not be too small.
R.3 Primary Outcome: Assessment of Rationales
The rationale statement associated with the SHI explains the importance of following safe handling instructions to prevent foodborne illness. Participants will be presented with five variants of a newly proposed SHI rationale statement (provided in Appendix Q). Using a drag-and-drop feature, they will rank (i.e., order) the statements in terms of how clearly each one communicates the dangers of foodborne illness. The three rationales with the highest ranking (i.e., the three winning choices) will be considered for inclusion with the SHI labels developed for the behavior change study.
When ranking involves an array of options and multiple winners as it does here, simple plurality voting can lead to suboptimal choice. In other words, ranking a set of five options into first, second, third, through fifth position does not produce the same results as a series of binary selections (i.e., where each choice is rated against every other choice in a head-to-head comparison). However, we are constrained by the fact that a run-off, or repeated choice, process is not possible. Various voting schemes have been proposed to address this problem and are detailed in the seminal paper by Levin and Nalebuff (1995). Although the literature offers no clear consensus (Risse, 2005), the alternative voting method proposed by Coombs addresses the three following criteria (Grofman & Feld, 2005):
Offers simplicity
Reduces the likelihood of selecting less favorable choices
Increases the likelihood of selecting more favorable choices
Under the Coombs rule, participants rank order their choices (in this case, the five versions of the rationales) from first place to kth place. A matrix is created where each option’s first through kth place rankings are recorded. The choice with the most last (kth) place rankings is removed and the votes of the eliminated choice (i.e., rationale) are redistributed. Redistribution occurs by assigning each participant’s vote to their next highest rank candidate. Consider the following example:
For example, if 200 participants’ first choice rationale received the most last-place votes during the first round of vote tallying, those votes would be transferred to each participant’s second choice and votes would be tallied again. If the difference in votes between the third- and fourth-place rationale was only 100 votes and all 200 participants in this example voted for the (currently placed) fourth-place rationale as their second choice, the transfer would be sufficient to elevate the fourth-place rationale to third place. For the present study, we will only require a single retallying of votes. At the end of the second round of tallying, the rationale with the fewest votes will be removed, and additional transfers will not affect the final outcome (selecting three rationales).
R.4 Develoing the Three SHI Labels to Test in the Behavior Change Study
Experts in risk communication will assign one of the three rationales to the each of the three SHI labels with the highest visual salience score to create the final three labels for testing in the behavior change study.
R.4 References
Grofman, B., & Feld, S. L. (2004). If you like the alternative vote (a.k.a. the instant unoff), then you ought to know about the Coombs rule. Electoral Studies, 23, 641–659.
Hanley, J. A., & McNeil, B. J. (1982). The meaning and use of the area under a receiver operating characteristic (ROC) curve. Diagnostic Radiology, 143(1), 29–36.
Levin, J., & Nalebuff, B. (199)5. An Introduction to Vote-Counting Schemes. Journal of Economic Perspectives, 9(1), 3–26.
MacMillan, N. A. (2002). Signal detection theory. In Steven’s Handbook of Experimental Psychology, Volume 4: Methodology in Experimental Psychology. H. Pashler and J Wixted (Eds.) New York: John Wiley and Sons.
Pett, M. A. (1997). Nonparametric Statistics for health care research statistics for small samples and unusual distributions. Thousand Oaks, CA: Sage Publications.
Risse, M. (2005). Why the count de Borda cannot beat the Marquis de Condorcet. Social Choice and Welfare, 25, 95–113.
SAS Institute Inc. (2013). SAS/STAT® 13.1 User’s Guide. Cary, NC: SAS Institute Inc.
1 The participant’s decision criterion is the “threshold” for deciding whether they recall the stimulus item. Participants with a low criterion will answer yes more often, resulting in more correct hits at the cost of incorrectly answering more false alarms.
2 The risk preference variable is an index created by summing and averaging the nine risk preference items in the survey (Questions 28–36). Experience with a foodborne illness is a dichotomous variable indicating whether the participant believes that they or a member of their immediate family experienced a foodborne illness in the past year (Question 41).
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Modified | 0000-00-00 |
| File Created | 0000-00-00 |
© 2026 OMB.report | Privacy Policy